Drinfeld-Sokolov-Satsuma-Hirota方程族及其廣義雙 Hamiltonian結(jié)構(gòu)

楊本朝，耿獻國

(1.信息工程大學 信息工程學院 河南 鄭州 450002； 2.鄭州大學 數(shù)學系 河南 鄭州 450001)

Drinfeld-Sokolov-Satsuma-Hirota方程族及其廣義雙Hamiltonian結(jié)構(gòu)

楊本朝1，耿獻國2

(1.信息工程大學 信息工程學院 河南 鄭州 450002； 2.鄭州大學 數(shù)學系 河南 鄭州 450001)

基于帶有兩個位勢的4×4矩陣譜問題，導出一族非線性演化方程，其中一個典型成員是Drinfeld-Sokolov-Satsuma-Hirota方程.進而證明了這族方程具有廣義雙Hamiltonian結(jié)構(gòu)并且在Liuovlle意義下是完全可積的.

Drinfeld-Sokolov-Satsuma-Hirota方程族； 廣義雙Hamiltonian結(jié)構(gòu)； 可積性

0 引言

文獻[1-2]獨立地引入非線性演化方程

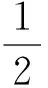
(1)

找到了這個方程的一個Lax對和一孤子解并發(fā)現(xiàn)它可作為KP族的四約化的特殊情況.文[3]應用Weiss方法給出這個方程的Backlund變換及其特解.文[4]借助 Cole-Hopf變換和顯函數(shù)的展開法研究了這個方程，并獲得孤子解、多孤子解和周期解等[5-6].

本文首先從帶有兩個位勢的4×4的矩陣譜問題出發(fā),

(2)

其中u,v是兩個位勢，λ是常值譜參數(shù)，利用Lenard遞推關(guān)系及零曲率方程導出一族非線性演化方程，其中一個是Drinfeld-Sokolov-Satsuma-Hirota方程(1)，另一個是五階非線性演化方程

(3)

當v=0時，方程(3)約化為五階KdV方程，進而證明了這族方程在Lax意義下是完全可積的.利用跡恒等式[7]獲得它們的雙Hamiltonian結(jié)構(gòu).

1 非線性演化方程族

為了得到與譜問題(2)相關(guān)的非線性演化方程族，我們求解定態(tài)的零曲率方程

Vx=[U,V],V=(Vij)4×4,

(4)

其中Vij=Vij(a,b)是關(guān)于λ的Laurent展開，即

(5)

把(5)代入(4)得

KG=λJG,G=(a,b)T,

(6)

其中K和J是兩個斜對稱算子，

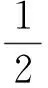
將(5)的后兩式代人(6)并比較λ相同冪的系數(shù)得:

KGj=JGj+1,JG0=0,

(7)

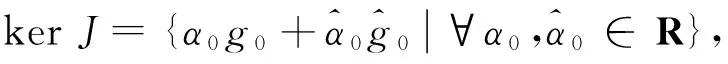
(8)

為了得到(7)式的一般解，引進兩組Lenard遞推方程：

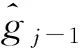
(9)

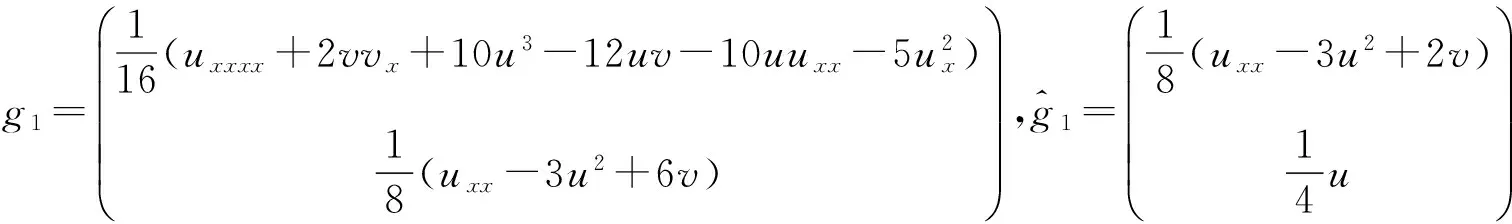
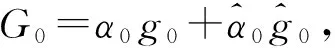
假定y滿足譜問題(2)和相應的時間發(fā)展式:

yt=V(m)y,V(m)=(λmV)+,m≥0,

(10)

其中+表示λ的非負次冪項，由(1)和(10)的相容性條件得到零曲率方程Utm-Vx(m)+[U,V(m)]=0，此即是非線性演化方程族

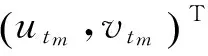
(11)

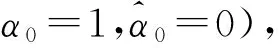
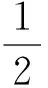
(12)

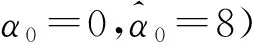
(13)

當t1=t時, (13)即為方程(3).

2 廣義雙Hamiltonian結(jié)構(gòu)和可積性

為了得到非線性演化方程族(11)的Hamilton結(jié)構(gòu)，首先計算式子：

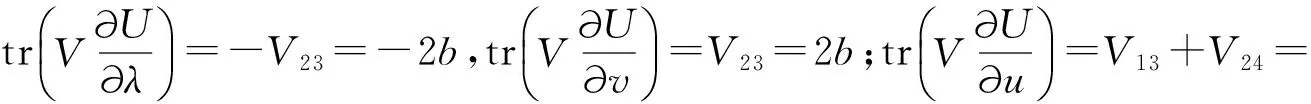
由跡恒等式[7]，可得：

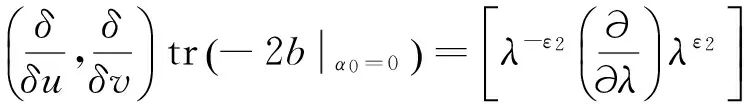
其中ε1，ε2是待定常數(shù).通過比較λ-j-1兩邊的系數(shù)得:

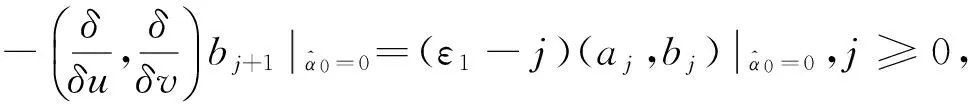
為了得到ε1，ε2的值，在式子中固定j=0，得到ε1=-3/4，ε2=-1/4.由此推出

則方程族(11)可寫為廣義雙Hamiltonian形式

(14)

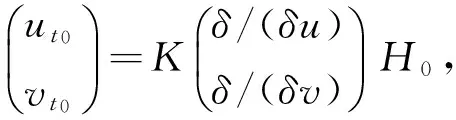
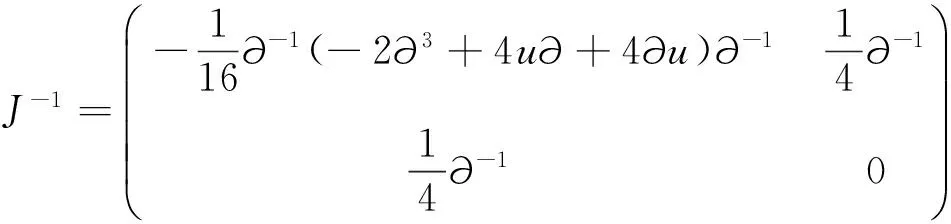
易證明K,J都是辛算子，滿足K=JL,JL=L*J.由此得Possion括號定義為

{f,g}=(δf/(δu),J(δg)/(δu)).

(15)

由(14)式得

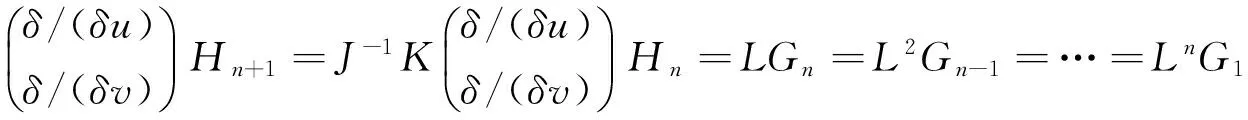
因此{Hn}是方程族ut=JLnf(s)的一列守恒密度，且滿足對合條件{Hn,Hm}=0，其中Possion括號由(15)式定義，所以方程族(11)是在Liouville意義下可積的.

[1] Drinfeld V G, Sokolov V V.Equations of Korteweg-de Vries type and simple Lie algebras [J].Dokl Akad Nauk SSSR, 1981, 258(1):11-16.

[2] Satsuma J, Hirota R.A coupled KdV equation is one of the four-reduction of the KP hierarchy [J].J Phys Soc Japan, 1982, 51 (10):3390-3397.

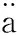
[4] Wazwaz A M.The Cole-Hopf transformation and multiple soliton solutions for the integrable sixth-order Drinfeld-Sokolov-Satsuma-Hirota equation[J].Appl Math Comput, 2009,207(1):248-255.

[5] 李雪梅, 楊運平.高階耦合非線性Schrodinger方程的單孤子解[J].鄭州大學學報:理學版, 2002, 34(3):13-15.

[6] 杜殿樓.駐定CG方程解的參數(shù)表示[J].鄭州大學學報:自然科學版,1998,30(1):12-17.

[7] Tu G Z.A trace identity and its applications to the theory of discrete integrable systems[J].J Phys A:Math Gen,1990,23(17):3903-3922.

Drinfeld-Sokolov-Satsuma-HirotaEquationsandGeneralizedBi-HamiltonianStructures

YANG Ben-chao1，GENG Xian-guo2

(1.InformationEngineeringUniversityofthePeoplesLiberationArmy,Zhengzhou450002，China; 2.DepartmentofMathematics,ZhengzhouUniversity,Zhengzhou450001,China)

A hierarchy of nonlinear evolution equations was derived from a matrix spectral problem with two potentials,in which a typical member was the Drinfeld-Sokolov-Satsuma-Hirota equation .It was shown that the hierarchy of nonlinear evolution equations possessed the generalized bi-Hamiltonian structures and was completely integrable in the Liuovlle sense.

Drinfeld-Sokolov-Satsuma-Hirota equations； generalized bi-Hamiltonian structures； integrability

O 175

A

1671-6841(2011)03-0031-03

2010-03-25

楊本朝(1981-)，男，助教，碩士，主要從事孤立子與可積系統(tǒng)研究，E-mail: yang_benchao@yahoo.com.cn .