氧樂果合成過程的PSO-回歸BP網絡建模方法

馮冬青，楊書顯

(鄭州大學 電氣工程學院 河南 鄭州 450001)

氧樂果合成過程的PSO-回歸BP網絡建模方法

馮冬青，楊書顯

(鄭州大學 電氣工程學院 河南 鄭州 450001)

為了提高模型效率，更好地反映實際系統的動態特性，根據氧樂果合成過程特點確定了PSO-回歸BP網絡結構.采用慣性權重動態調整的粒子群算法進行初始尋優，并基于改進的BP算法對優化的網絡權閾值進一步精確優化，建立了氧樂果合成過程的PSO-回歸BP網絡模型.仿真結果表明，所建模型誤差小、收斂速度快、網絡泛化能力強，能更好地反映實際對象特點.

粒子群算法； 回歸BP網絡； 氧樂果合成； 溫度對象

0 引言

氧樂果是農業生產中廣泛使用的一種農藥，其質量的優劣對農業生產有很大的影響，為其生產過程建立較為精確的數學模型，將有利于改善控制效果，提高產品質量與經濟效益.氧樂果合成過程是典型的間歇生產過程，反應釜溫度對象具有多變量、非線性、時變、分布復雜等特點，因此利用傳統方法建模非常困難.

以往的氧樂果合成過程建模研究中，曾在BP網絡的基礎上加上TDL環節，建立了回歸網絡模型，采用BP算法進行學習訓練[1-2].文[3]基于遺傳算法優化的神經網絡模型，用遺傳算法對BP神經網絡進行優化取得了較好效果，但仍避免不了一些缺點.粒子群優化(particle swarm optimization，PSO)算法采用速度位移模式[4-5]，保留全局搜索策略，概念簡單，具有計算復雜度低、收斂速度快，僅有少量參數需要調整，操作簡單、易實現等特點，作為一種全局優化算法為神經網絡的優化問題提供了便捷高效的解決方法，并已在實際問題的應用中顯示出極大的優越性[6-7].本文將粒子群優化算法與回歸BP網絡相結合，建立氧樂果合成過程的PSO-回歸BP網絡模型，并用歷史數據對網絡進行訓練和測試，結果表明所建模型誤差小、網絡泛化能力強.

1 氧樂果合成過程特性分析

氧樂果合成反應是一個劇烈的放熱反應，反應物是一甲胺和精酯，反應產物是氧樂果粗原油，反應設備主要包括計量罐、反應釜、冷卻系統等.氧樂果的合成反應過程對溫度和一甲胺投料速度均有較高的要求.

生產過程中通常先將精酯裝入外壁纏有冷卻鹽水管道的反應釜中，將其冷卻到-20 ℃以下，之后計量罐中的一甲胺開始滴注到反應釜內并進行均勻攪拌，在冷卻系統的作用下實現合成反應.反應初期由于反應釜中精酯含量較高，投入的一甲胺還比較少，所以反應產生的熱量很快被吸收，溫升較慢.隨著一甲胺投入量的增加，反應釜溫度開始迅速攀升，此時要減小一甲胺流量，抑制合成反應的放熱量和放熱速度，從而使反應溫度的上升趨勢放緩，防止由于溫升速率過高造成溫度超標.當反應釜溫度上升到-14～-12 ℃時，應當保持適當的投料速度，使系統處于熱平衡狀態，反應溫度在小范圍內變化.當一甲胺的剩余量較少時，由于反應釜內的精酯大部分已經被消耗掉，反應釜溫度不會快速攀升，在溫度不超過-12 ℃的前提下盡快完成一甲胺投料.

該反應過程受到很多干擾因素的影響，具有多變量特性.其中一甲胺流量、反應進行時間、冷卻鹽水溫度、一甲胺累積投料量對反應釜溫度的影響較為顯著.此外，精酯含量、一甲胺含量、冷卻系統熱交換的好壞等對反應釜溫度也有一定的影響.通過對生產過程的特性分析知道該反應過程還具有明顯的非線性和時變特性.針對此類復雜系統，無法采用傳統方法建立精確的模型，因此有必要研究智能建模方法.

2 氧樂果合成過程建模

近年來動態回歸網絡受到了人們的普遍關注，回歸網絡的一個最顯著特點就是它的輸出端信號通過延時環節或者一階慣性環節的反饋機構連接到輸入端.其代表是Hopfield網絡和Elman網絡,此類網絡在建立動態系統模型方面有其長處，但同時應指出它采用的是動態反傳算法，其運算量比靜態BP算法大得多.因此，一些研究者嘗試將BP算法中采用的梯度下降法推廣到回歸網絡中，由此產生了回歸BP網絡.

氧樂果生產過程中的溫度是每隔一分鐘采樣一次，前一分鐘的溫度對當前時刻的溫度可能產生重大影響.所以我們要采用回歸BP網絡，將溫度輸出變量延時一拍作為神經網絡的一個輸入，使網絡同時具有前饋和反饋機制，可以充分利用輸入輸出數據的動態信息，使其一開始就能夠跟蹤對象的特性，以期獲得更為精確的溫度對象模型.

2.1確定回歸BP網絡模型結構

影響反應釜溫度的主要因素有4種，它們之間關系可以表示為

Tfyf=f(Fyja,Tlqs,sumyja,tfy)，

(1)

其中，Fyja為一甲胺流量；Tlqs為冷卻鹽水的溫度；sumyja為一甲胺的總投料量；tfy為反應進行時間.

那么，網絡的輸入變量就為影響反應釜溫度的4個主要因素及反應釜前一時刻的溫度Tfyf(t-1)；輸出變量為反應釜溫度Tfyf；網絡隱含層節點數先由經驗公式確定為12個，后經試驗方法驗證12個較為理想.故本文采用的神經網絡結構就為5×12×1，輸入層為5維的輸入向量和一個閾值結點，該閾值的存在保證了網絡的收斂特性.中間層有12個神經元和一個閾值結點，輸出層只有一個神經元,為反應釜溫度輸出.相鄰兩層神經元之間以全連接的方式相連.

2.2優化網絡參數的PSO算法

對BP模型的初始權閾值先采用一定的策略進行優化，然后再采用BP算法進行二次優化確定最終權閾值可以提高模型的運行效率[8].PSO算法的特點使其在神經網絡參數優化方面已獲得較為廣泛的應用[9-10].

楊偉東畢業于位于江蘇南京的河海大學中文系，并不出眾的學歷，加上又是在海歸遠“吃香”于土鱉的外企，他還是在2009年到2011年，從一名普通職員一路升到了諾基亞大中國區市場營銷總監。之后，楊偉東等人創立了麥特文化，一只腳踏進了文娛圈。

PSO算法是基于群體的，最初是為了在二維空間圖形化模擬鳥群優美而不可預測的運動[11]，從這種模型中得到啟發并用于解決優化問題，后來將其推廣到D維空間.每個優化問題的解就是搜索空間中的一只鳥，鳥被抽象為沒有質量和體積的微粒點,鳥在搜索空間中以一定的速度飛行，這個速度根據它本身的飛行經驗和同伴的飛行經驗來動態調整.第i個微粒在D維空間的位置矢量表示為xi(xi1,xi2,…,xiD)T，速度矢量表示為vi=(vi1,vi2,…,viD)T.每個粒子都有一個被優化的函數決定的適應值，它經歷過的最好位置(有最好的適應值)記為pi=(pil,pi2,…,piD)，也稱為pbest，這個可看作粒子本身的飛行經驗.群體所有微粒經歷過的最好位置用Pg表示，也稱為gbest，這個可看作是粒子同伴的飛行經驗.PSO算法是一種基于迭代的優化工具，對于每一代，它的第d維(1≤d≤D)根據方程(2)、(3)進行變化：

vid(t+1)=w(t)×vid(t)+c1×r1×(pid(t)-xid(t))+c2×r2×(pgd(t)-xid(t)),

(2)

xid(t+1)=xid(t)+vid(t+1).

(3)

其中，i=1,2,…，M，M為該群體中粒子總數；d=1,2,…,D，D為解空間維數，即自變量的個數；w為慣性權重函數，通常在進化過程中線性遞減；t為進化代數；c1和c2為位移變化的限定因子，通常為2；r1和r2為兩個在[0,1]范圍里變化的隨機值.此外，微粒的速度vi被一個最大速度vmax所限制，控制粒子的位移不至過大，如果當前對微粒的加速導致它在某維的速度vid超過該維的最大速度vmax,d，則該維的速度被限制為最大速度vmax,d.迭代終止條件一般選為最大迭代次數或滿足較好的適應值.

2.3數據預處理

從現場采集的歷史數據中取出4組，其中Fyja，T1qs和Tfyf是可以直接測量的數據；sumyja可由計量罐液位計算得到，反應時間tfy由反應時刻t計算得到.因為輸入輸出數據存在測量噪聲，系統本身也存在動態干擾，故在系統辨識之前有必要對原始數據進行預處理.首先應對數據進行壞值剔除，消除粗差；其次將數據進行隨機誤差與系統誤差預處理；最后按(4)式進行歸一化處理.

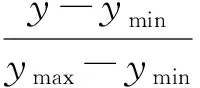
(4)

式中y,y′分別為歸一化前后的數據，ymin,ymax分別是所有采樣數據中的最小值和最大值.

將歸一化后的數據取3組作為訓練樣本，另一組作為測試樣本.其中Fyja，T1qs，sumyja,tfy,Tfyf構成輸入矩陣P，反應釜溫度構成目標矩陣Q.

基于PSO算法的優點，將其與BP算法結合起來形成混合算法，對回歸BP神經網絡的權閾值進行優化.首先我們根據已確定好的回歸BP網絡結構計算粒子群神經網絡的維數；然后將神經網絡的全體權值和閾值向量映射為粒子群搜索空間中的位置元素；其次采用粒子群算法尋找模型的初始權值與閾值；最后再采用改進的BP算法訓練經過粒子群算法尋優的初始權值與閾值，得到最終模型.

建模過程用matlab程序實現，具體流程如下：

Step1根據已確定好的回歸BP網絡結構5×12×1，計算粒子群神經網絡的維數n=(5+1)×12+(12+1)×1=85.

Step2確定粒子群規模及迭代次數.對于粒子個數m，通常在10～50之間取值，文中取為40.將神經網絡的全體權值和閾值向量映射為粒子群搜索空間中的位置元素，則粒子搜索空間的維數即為85.迭代次數Tmax=150.

Step3慣性因子w的設置.慣性權重用來控制粒子以前速度對當前速度的影響，它將影響粒子的全局搜索能力和局部搜索能力，較大的w有利于跳出局部極小點，較小的w有利于算法收斂.但由PSO微粒的搜索特征不難發現[12]，線性減小策略中w保持較大值和較小值的時間都很短，不能很好滿足開始搜索速度快些、搜索后期速度慢些的要求.本文w采取(5)式按余弦規律遞減的策略，使w由0.9動態遞減至0.1.

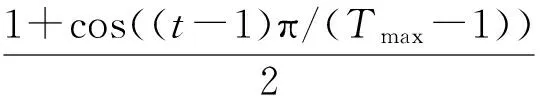
(5)

式中，Tmax為最大迭代次數；t為當前迭代次數；wmax=0.9；wmin=0.1.

Step4確定適應度評價函數.文中適應度函數取為訓練均方誤差函數，

(6)

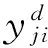
Step5速度與位置初始化[13].隨機生成m個個體，每個個體由兩部分組成，第一部分為粒子的速度矩陣，第二部分代表粒子的位置矩陣.由于BP 神經網絡的權值與閾值一般初始化為[-1,1] 之間的隨機數，故將粒子群中每個粒子位置參數均取為[-1,1]之間的隨機數作為PSO 算法的初始解集.

Step6輸入訓練樣本的輸入矩陣和目標矩陣，計算網絡的輸出，并根據(6)式評價每個粒子在神經網絡訓練樣本下的適應度.

Step7進行極值更新.比較每個粒子的適應值和pbest，若粒子當前適應度優于pbest,pbest被當前位置替換；若所有粒子的當前最優適應值優于gbest,gbest被當前最優位置替換.

Step8根據(2)、(3)和(5)式進行粒子速度和位置的更新，即調整神經網絡的權值與閾值.

Step9檢驗是否符合結束條件，如果當前的迭代次數達到了預先設定的最大次數(文中設為150次)或達到最小誤差要求，則停止迭代，轉Step10，否則返回Step6繼續進行迭代.

Step10算法停止迭代時，Pg對應的值即為訓練問題的最優解，即回歸BP網絡的權值與閾值.

Step11回歸BP神經網絡模型中隱含層傳輸函數取為“tansig”，輸出層傳輸函數取為“logsig”；網絡訓練目標誤差取為0.000 1.將Step10得到的最優解代入回歸BP神經網絡模型中，采用改進的BP算法(添加動量項與自適應學習率相結合)進行二次訓練學習，最終形成所需的對象模型.

3 模型驗證與分析

保存得到的最終對象模型，取出測試樣本(與訓練樣本經過相同預處理)對訓練好的神經網絡模型進行驗證.為對比起見，我們也建立了BP網絡模型進行驗證，驗證結果如圖1和圖2所示.從圖中可以看出，BP網絡模型誤差較大，通過計算得到BP網絡模型最大誤差高達12.4% .這些誤差比較大的點出現在合成反應的溫度上升階段，這個階段合成反應的總體放熱效果開始超過系統的冷卻效果，系統的熱平衡被打破，反應溫度開始快速增長.而PSO-回歸BP網絡具有反饋機制，充分利用了輸入輸出數據之間的關系，較好地跟蹤對象特性，尤其是在溫度上升階段誤差明顯減小，更好地模擬了溫度過程的變化，曲線擬合精度更高，最大誤差只有4.9%，最小誤差還不足0.03%.

圖3所示為PSO尋找回歸BP網絡模型參數的最優適應度變化曲線，由圖可知經過100余次迭代粒子群算法已找到初步最優解，在此基礎上采用改進的BP算法繼續學習訓練，只用9步就達到了訓練目標，網絡收斂很快，訓練誤差曲線如圖4所示，而單獨采用改進的BP算法經過2 000余次迭代還遠達不到訓練目標.這主要是由于PSO算法通過動態遞減的慣性權重協調了全局搜索與局部搜索，既能以較大的概率保證最優解，克服BP算法局部最優的缺陷，又可以提高局部區域的收斂速度，避免在局部區域搜索過程中的收斂停滯現象.

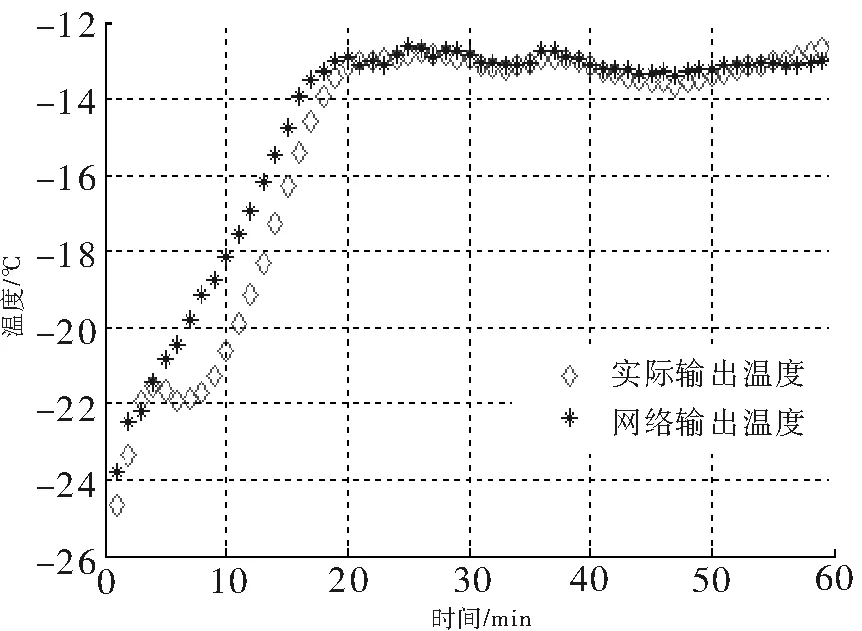
圖1 基于BP網絡的溫度輸出驗證曲線Fig.1 Verifying curve of temperature output based on BP network

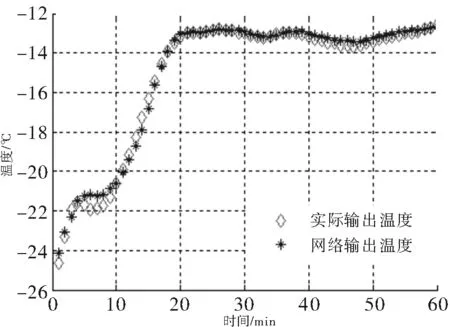
圖2 PSO-回歸BP網絡的溫度輸出驗證曲線Fig.2 Verifying curve of temperature network output of PSO-recurrent BP network

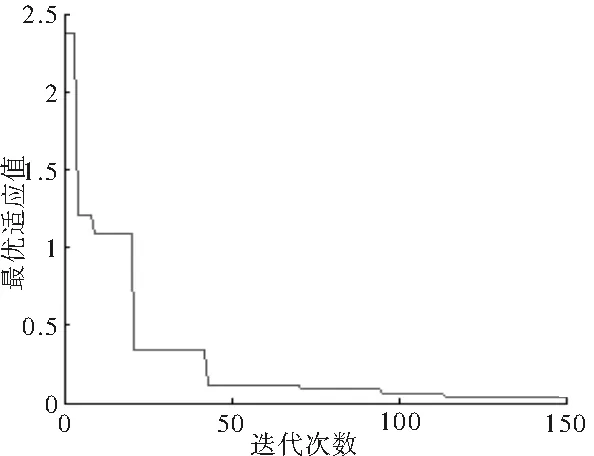
圖3 PSO最優適應度曲線Fig.3 Curve of fitness of PSO

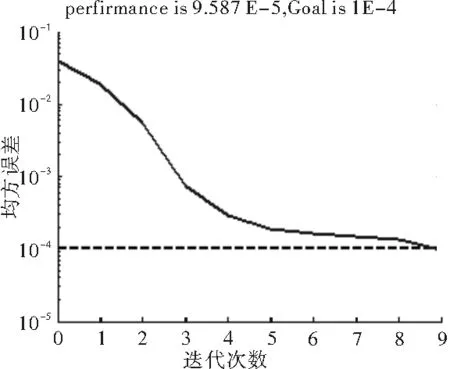
圖4 PSO-回歸BP網絡訓練誤差曲線Fig.4 Curve of training error of PSO-recurrent BP network

4 結論

PSO優化算法對神經網絡模型的訓練操作簡單，計算復雜度低，它能有效地搜索到神經網絡的最優權值和最佳閾值，而回歸網絡能更好地體現系統的動態特性.本文將二者相結合，建立了氧樂果合成過程溫度對象的PSO-回歸BP網絡模型，仿真結果表明該模型結合了粒子群算法的全局尋優能力和 BP神經網絡算法的局部搜索優勢，更體現了實際系統的動態性能，較真實地反映了氧樂果合成反應的溫度特性，具有較高的精度、較好的性能，可以用來研究氧樂果合成過程溫度自動控制系統的優化控制算法，為實現綜合優化控制提供有力的依據.

[1] Yang J M, Kao C Y.A robust evolutionary algorithm for training neural networks[J].Neural Computing and Application,2001,10(3):214-230.

[2] 馮冬青，張新征，費敏銳.基于回歸神經網絡的氧樂果合成過程建模與仿真[J].系統仿真學報，2005,17(6):1522-1524.

[3] 王曉沛.基于神經網絡的智能控制方法研究[D].鄭州：鄭州大學，2007.

[4] Yang Shuxia.Neural network forecast under the organic hybrid model of genetic algorithm and particle swarm algorithm[C]//Proceedings of the 2008 International Conference on Wavelet Analysis and Pattern Recognition.Hong Kong, 2008:30-31.

[5] AlRashidi M R， El-Hawary M E.A survey of particle swarm optimization applications in electric power systems[J].IEEE Transactions on Evolutionary Computation,2009,13(4):913-918.

[6] 田麗，夏新運，蔣慧，等.基于PSO-BP混合算法的短期電力負荷預測[J].自動化與儀器儀表,2009(2):40-41.

[7] 孫世昶，劉洪波，林鴻飛，等.一種離散粒子群算法在對等網絡鄰接選擇問題中的應用[J].鄭州大學學報：理學版，2009,41(1)：86-89.

[8] 岳琳，張宏偉，王亮.粒子群優化算法在城市需水量預測中的應用[J]天津大學學報：自然科學版，2007,40(6):742-746.

[9] 梁本亮, 王增忠, 孫富學.基于PSO的結構損傷檢測應用研究[J].鄭州大學學報：理學版，2006,38(4):93-97.

[10] 楊光友，劉瓊.前向神經網絡粒子群優化學習算法研究[J].廣西師范大學學報：自然科學版，2008，26(3):151-156.

[11] Kennedy J, Eberhart R C.Particle swarm optimization [C]//IEEE International Conference on Neural Networks. Piscataway, 1995:1942-1948．

[12] 陳國初，俞金壽.增強型微粒群優化算法及其在軟測量中的應用[J].控制與決策：2005，20(4)：377-381.

[13] 王海軍，白玫，賈兆立，等.基于粒子群神經網絡的期貨價格預測[J].計算機工程與設計,2009，30(10)：2428-2430.

ModelingMethodofPSO-recurrentBPNetworkforOmethoateSynthesisProcess

FENG Dong-qing, YANG Shu-xian

(SchoolofElectricalEngineering,ZhengzhouUniversity,Zhengzhou450001,China)

In order to improve the model efficiency and show dynamic characteristic of the system, the modeling method of PSO-recurrent BP network for omethoate synthesis process was studied.Firstly, the structure of PSO-recurrent BP network was determined according to the features of the object.Secondly, PSO algorithm was used to optimize the weight and threshold of BP neural network.Finally, the improved BP algorithm was used to train the pre-optimized weight and threshold for getting further accurate parameters of the model.The simulation results showed that this model not only had small error, fast convergence speed and strong ability of network generalization, but also show characteristics of the actual object well.

PSO algorithm； recurrent BP neural network； omethoate synthesis； temperature object

TP 391.9

A

1671-6841(2011)03-0113-05

2010-05-12

國家自然科學基金資助項目，編號60774059.

馮冬青(1958-),男,教授,主要從事智能控制理論與應用研究，E-mail:dqfeng@zzu.edu.cn；通訊作者：楊書顯(1983-),女,碩士研究生, 主要從事智能控制理論與應用研究.