結合廣義Armijo步長搜索的一類記憶梯度算法

朱 帥，王希云

(1.山西大同大學 工學院 山西 大同 037003； 2.太原科技大學 應用科學學院 山西 太原 030024)

結合廣義Armijo步長搜索的一類記憶梯度算法

朱 帥1，王希云2

(1.山西大同大學 工學院 山西 大同 037003； 2.太原科技大學 應用科學學院 山西 太原 030024)

給定記憶梯度算法搜索方向中的參數一個假設條件，從而確定它的一個取值范圍, 使其在此范圍內取值均能得到目標函數的充分下降方向，由此提出一類新的記憶梯度算法.在去掉迭代點列有界和廣義Armijo步長搜索下,討論了算法的全局收斂性，且給出了結合形如共軛梯度法FR,PR,HS的記憶梯度法的修正形式.數值實驗表明,新算法比Armijo線搜索下的共軛梯度法FR、PR、HS和記憶梯度法更穩定、更有效.

無約束優化; 記憶梯度法; 廣義Armijo線搜索; 全局收斂性

0 引言

考慮無約束優化問題

minf(x),x∈Rn,

(1)

文獻[1]中提出一個算法類，其中搜索方向為：

(2)

文獻[2-3]提出的算法中搜索方向dk及其參數βk的假設條件為

本文在文獻[2-3]的理論基礎上，對文獻[1]的搜索方向dk中的參數βk給出了類似的假設，從而建立了求解問題(1)的一個新的記憶梯度算法，并在去掉迭代點列{xk}有界和廣義Armijo步長搜索下,討論了算法的全局收斂性.

1 算法及其性質

假設

式中θk為gk和gk-1的夾角.

算法如下：

初始步:μ1,μ2∈(0,1),且μ1≤μ2；γ1,γ2>0；Δ>0為常數.

Step3ak滿足廣義Armijo搜索[3]：

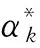
Step4xk+1=xk+αkdk,k=k+1,轉Step1.

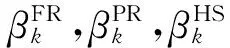
注3結合形如共軛梯度法FR,PR,HS的記憶梯度法和本文算法，可選取βk為:

引理1若xk不是問題(1)的穩定點,則有

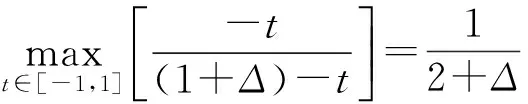
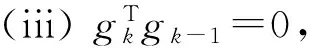
(c)證明可參考文獻[2]中引理3.

2 算法全局收斂性

以下假設算法產生的點列{xk}為一無窮點列,全局收斂結果如下：

定理1假設f(xk)∈C1,則

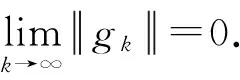
證明參考文獻[3]中定理4的證明.

3 數值實驗

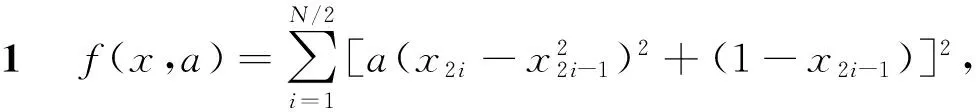
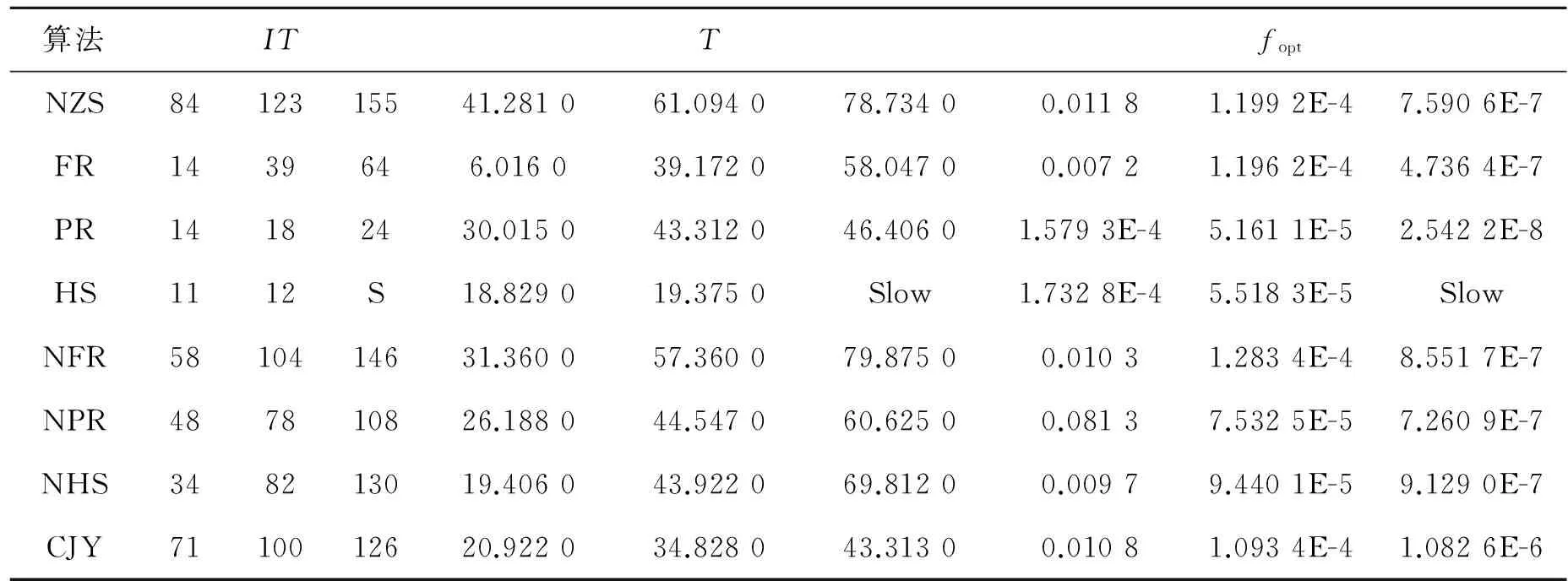
表1 例1的數據

表2 例2的數據

從以上數值實驗和比較可以看出，本文算法雖然有時不如其他算法，但是它不隨函數改變而發生明顯變化，即本算法收斂速度均勻，計算效能良好，適合求解大規模無約束優化問題.故本算法是有效的.

[1] 時貞軍. 無約束優化的超記憶梯度算法[J]. 工程數學學報, 2000, 17(2): 99-104.

[2] 孫清瀅,劉新海.結合Armijo步長搜索的一類新記憶梯度算法及其特征[J]. 石油大學學報, 2003, 27(5): 129-132.

[3] 孫清瀅. 結合廣義Armijo步長搜索的一類新的共軛梯度算法及其特征[J]. 工程數學學報, 2003, 20(1): 14-20.

[4] Shi Zhenjun. A new super-memory gradient method for unconstrained optimization[J]. 數學進展, 2006,35(3): 265-274.

AClassofMemoryGradientSearchAlgorithmwithGeneralizedArmijoStepSize

ZHU Shuai1, WANG Xi-yun2

(1.SchoolofEngineering,ShanxiDatongUniversity,Datong037003,China; 2.SchoolofAppliedScience,TaiyuanUniversityofTechnology,Taiyuan030024,China)

An assumed condition of parameters was given in the memory gradient directions to determine values that these parameters may take.The values range ensure the objective function was sufficient descent,and a new memory gradient algorithm was presented.The convergence was discussed without the generalized Armijo step size rule and the assumed condition that the sequence of iterates was bounded.Combing FR,PR,HS methods with the new method,the modified of the memory gradient algorithm was given.Numerical results showed that the new algorithm was more stable and efficient that conjugate gradient methods FR,PR,HS and Armijo step size rule.

unconstrained optimization；memory gradient method；generalized Armijo line search；global convergence

O 221.2

A

1671-6841(2011)03-0016-03

2010-07-18

山西省自然科學基金資助項目, 編號2008011013.

朱帥(1980-), 男, 講師, 碩士, 主要從事最優化理論與方法研究, E-mail:sxdtdxzs@126.com; 通訊作者:王希云(1964-), 女, 教授, 主要從事最優化理論與方法研究, E-mail:tykdwxy@126.com.