關于力學系統(tǒng)的自由度的討論

劉麗華 徐 美 邱紅梅

(北京科技大學物理系,北京 100083)

關于力學系統(tǒng)的自由度的討論

劉麗華 徐 美 邱紅梅

(北京科技大學物理系,北京 100083)

對大學物理教材中廣泛采用的自由度的概念進行了討論,并用簡潔易懂的方法計算了N個粒子組成的系統(tǒng)的自由度.

自由度;N個粒子系統(tǒng)

在大學普通物理的教學過程中,很多內容都要用到“自由度”這一概念,其中最典型的當屬熱學中的“能量按自由度均分定理”:在溫度為 T的平衡狀態(tài)下,系統(tǒng)中分子的每個自由度都有相等的平均熱運動動能,其大小等于kT/2[1～5].所以,當我們分析一個熱力學系統(tǒng)的內能時,關鍵問題就是:如何確定該系統(tǒng)分子的自由度數(shù)?

1 “自由度”的概念

關于“自由度”或“自由度數(shù)”的定義,大學物理教材中常見的說法有以下幾種:“所謂系統(tǒng)的自由度,就是決定這個系統(tǒng)在空間的位置所需要的獨立坐標的數(shù)目[1]”;“確定一個物體在空間的位置時,需要引入的獨立坐標的數(shù)目稱為該物體的自由度數(shù)[2]”;“要確定一個力學系統(tǒng)的空間位形需要一定數(shù)目的相互獨立的坐標量,這相互獨立的坐標量數(shù)目稱為力學系統(tǒng)的自由度數(shù)[3]”;“決定一物體的位置所需要的獨立坐標數(shù),稱為這一物體的自由度[4]”,等等.

對于雙原子分子,如果不考慮原子間相對位置的變化(即認為系統(tǒng)是剛性的),則系統(tǒng)共有 5個自由度,其中包括 3個平動自由度和 2個轉動自由度.這一結論大致可以通過下面兩種方法來證明.

方法一一個可以在空間自由運動的質點需要用 3個獨立坐標 (如 x,y,z)來決定它在空間的位置,因此一個質點有 3個自由度.而雙原子分子可以看成是一個“兩質點系統(tǒng)”,則需要用 (x1,y1,z1)和 (x2,y2,z2)來分別確定質點 1和質點 2的位置,也就是說,一共需要 6個坐標 (x1,y1,z1,x2,y2,z2)來確定系統(tǒng)空間位形.但是,對于剛性雙原子分子而言,由于兩個質點間的距離 (設為 r)是固定的,并有在這個方程的約束下,6個坐標中只有 5個是獨立的,所以雙原子分子具有 5個自由度[1].

方法二雙原子分子 (兩個原子均看作質點)中的兩個原子是由一個化學鍵連接在一起的.對于這樣的力學系統(tǒng),我們可以先確定其質心的位置,之后再利用方位角來確定兩個原子之間連線的方向即可.確定質心位置需要 3個獨立坐標,此即系統(tǒng)的 3個“平動自由度”;關于質點間連線的方向,如圖1所示,在直角坐標系中,連線與 x、y、z軸的夾角分別設為α、β、γ,若α、β、γ已知 ,那么連線的方向也就確定了.由于1,所以這 3個方位角中只有 2個是獨立的,此即系統(tǒng)的 2個“轉動自由度”[2,4,5].

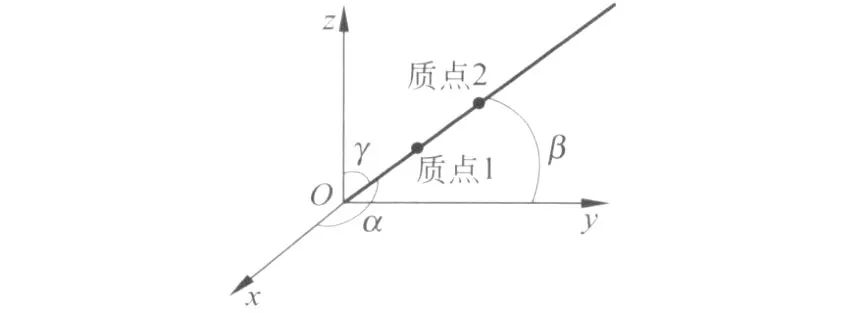
圖1 雙原子分子的轉動自由度

在熱力學中,剛性雙原子分子系統(tǒng)的內能已為實驗所驗證,也就是說,“剛性雙原子分子具有5個自由度”這一結論是被間接證實了的,因此是正確的.按照前述教材中“自由度”的概念,只需 5個坐標即可完全確定剛性雙原子分子的空間位形.

由此看來,前述諸多“自由度”的概念都存在值得商榷的地方.《中國大百科全書·物理學 II》中對于“自由度”的定義如下:“單值地確定某一力學體系的運動狀態(tài)所必須的、互相獨立并可以自由變動的物理量的數(shù)目就稱為某一力學體系的自由度[6].”這里需要強調的是“可以自由變動”這個條件.也就是說,某一變量必須可以在一定范圍內自由變動,即連續(xù)變化,才可以稱作 1個自由度.如果一個坐標量只有若干個分立值可取,則不能成為一個自由度.例如,在直角坐標系中,如果 x和 y可以任意取值,而 z只有兩個可能的取值,這樣確定下來的是兩個和 z軸垂直的平面 (如圖2),而非一個三維的空間,因此 z不可以稱為 1個自由度.因此,筆者認為,教科書上給出的雙原子分子自由度的推導是正確的,但是自由度的概念應表述為:完全確定一個物體的空間位形所需要的相互獨立并且可以任意取值的坐標數(shù)目.這樣,雖然z2和γ都有兩個可能的取值,卻不能成為一個自由度.那么,“剛性雙原子分子具有 5個自由度”的結論就嚴謹了.

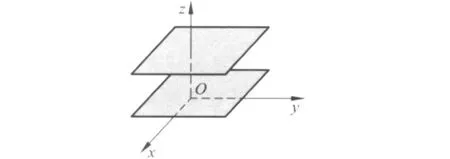
圖2 兩個可能的 z值確定的兩個平面

2 關于多質點系統(tǒng)的自由度

對于多質點系統(tǒng) (多原子分子)的自由度,教科書中指出:“一般的講,如果一個分子由 N個原子組成,則它最多有 3N個自由度,其中 3個是平動的,3個是轉動的,其余 (3N-6)個是振動的[4,5].”這一結論的嚴格證明超出了工科和低年級理科學生的理論知識范圍,因此在大多數(shù)普通物理教材中,上述結論是直接給出的,并沒有具體的證明過程,因而給學生造成了一定的困擾.下面我們給出非常簡單且容易被工科學生理解和接受的推導.

首先來分析雙原子分子.如前所述,剛性雙原子分子有 3個平動自由度和 2個轉動自由度;而對于非剛性分子,由于兩個原子可以在彼此連線的方向上做微小振動,因此還需要確定兩質點間的相對位置.如圖3所示,以質點 1為原點,過質點1和2的連線為x′軸,則只需一個坐標x′2即可確定質點 2的位置,此即 1個“振動自由度”.因此,雙原子分子共有 6個自由度:3個平動自由度,2個轉動自由度,1個振動自由度.

圖3 雙原子分子的振動自由度

再來看三原子分子.一般情況下,三原子分子可以看成是 3個質點不規(guī)則地組合在一起.和雙原子分子一樣,三原子分子也需要用 3個獨立坐標確定其質心的位置,即有 3個平動自由度;另需要 2個獨立坐標確定通過質心的任意軸的方位,以及一個獨立坐標 (例如φ)來確定系統(tǒng)繞此軸的角度 (如圖4(a)),所以系統(tǒng)共有 3個轉動自由度.此外,為了確定質點間的相對位置,在 3個質點確定的平面內,以質點 1為原點,過質點 1和 2的連線為 x′軸建立二維直角坐標系 (如圖4(b)),則確定質點2的位置需要一個坐標,確定質點3的位置需要兩個坐標也就是說,需要3個獨立坐標來確定質點間的相對位置,此即 3個振動自由度.因此,三原子分子共有 9個自由度:3個平動自由度,3個轉動自由度,3個振動自由度.

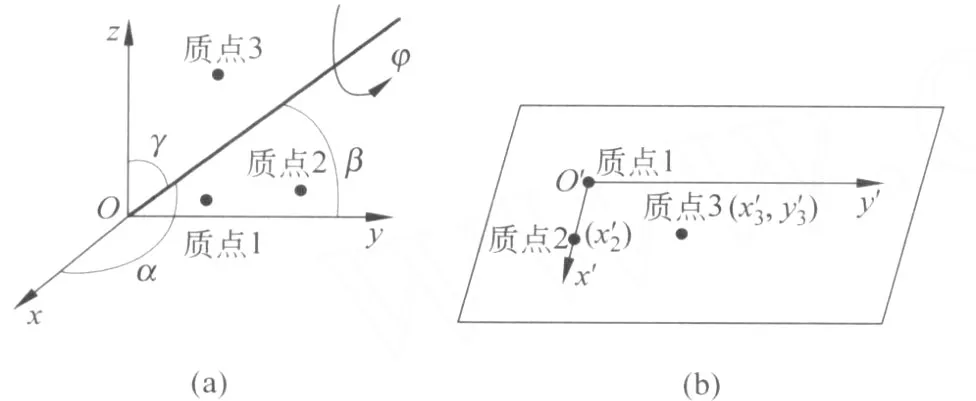
圖4 三原子分子的 (a)轉動自由度和 (b)振動自由度

進一步來分析四原子分子.和三原子分子類似,四原子分子具有 3個平動自由度和 3個轉動自由度.下面重點分析四原子分子的振動自由度.如圖5所示,質點 1、2和 3確定了一個平面,以這個平面為 X′O′Y′平面 (同三原子分子)建立三維直角坐標系.除了確定質點 2和 3所需要的 3個獨立坐標之外,確定質點4的位置又需要3個獨立坐標,所以系統(tǒng)一共有3+3=6個振動自由度.這就是說,四原子分子共有 12個自由度:3個平動自由度,3個轉動自由度,6個振動自由度.

圖5 四原子分子的振動自由度

以此類推,在三原子分子的 3個振動自由度的基礎上,每增加一個原子,系統(tǒng)就需要增加 3個獨立坐標來描述新增原子的相對位置,即增加 3個振動自由度.

總的來說,對于振動自由度,

單原子分子:0;

雙原子分子:1;

三原子分子:3;

四原子分子:3+1×3=6;

五原子分子:3+2×3=9;

…

…

N原子分子:3+(N-3)×3=3N-6.

綜上所述,N(N≥3)個粒子組成的系統(tǒng)共有3N個自由度,其中包括:3個平動自由度 (確定質心的位置),3個轉動自由度 (確定系統(tǒng)的方位),以及(3N-6)個振動自由度 (確定質點間的相對位置).

對于剛性分子,由于在運動過程中分子的大小和形狀都不發(fā)生變化,所以分子內任意兩個原子間的距離都是固定不變的.在這種情況下,剛性分子中的 (3N-6)個振動自由度被“凍結”,系統(tǒng)的振動自由度為零.

[1] 程守洙,江之永.普通物理學 上冊 第六版[M].北京:高等教育出版社,2006.111,177～178

[2] 張三慧.大學物理學 熱學 第二版[M].北京:清華大學出版社,2000.44～46

[3] 張玉民,阮耀鐘.普通物理學教程之二·熱學 第一版[M].北京:高等教育出版社,1991.328

[4] 趙凱華,羅蔚茵.新概念物理學 熱學 第二版 [M].北京:高等教育出版社,2005.80～81

[5] 李椿,章立源,錢尚武.熱學 第一版[M].北京:高等教育出版社,1978.95～96

[6] 中國大百科全書·物理學 II第一版[M].北京:中國大百科全書出版社,1987.1279

DISCUSSION ON DEGREE OF FREEDOM IN THE MECHANICAL SYSTEM

Liu Lihua Xu Mei Qiu Hongmei
(Department of Physics,Beijing Science and Technology University,Beijing 100083)

The concept“degree of freedom”used widely in university physics teaching materials has been discussed.The degree of freedom for a N-particle system has been calculated by using a simple method which is easy to understand.

degree of freedom;N-particle system

2010-09-27)