著陸作用下月塵激揚的三維離散元分析

陸 鑫 黃 勇 李 雯,2 趙 瑢 王 浚

(1 北京航空航天大學航空科學與工程學院,北京 100191)

(2 米蘭理工大學機械工程系機器人技術實驗室,意大利 米蘭 20156)

1 引言

月塵是月球環境重要的組成部分,是月球探測中不可忽視的影響因素。月塵是松散的顆粒群,在微流星撞擊、月面明暗交界靜電效應、宇航員行走、探測車行駛、探測器著陸等一定外力作用下會產生揚塵。探測器在月面著陸過程中將與月塵顆粒發生碰撞,會導致月塵顆粒揚起懸浮。揚起和懸浮的月塵顆粒因其粘附特性會附著在與其接觸的各類表面上,影響航天器和探測儀器的可靠性以及航天員的身體健康[1]。因此,研究月塵的揚起和漂浮機理及過程對于保障和提高月面探測器的可靠性具有重要意義。

國內外針對月塵做了較多的實驗和仿真研究。根據公開的研究報道,內容涉及月塵顆粒的尺度分布[2]、微觀形態和毒性作用[3]、粘附特性[4]、靜電力作用下運動[5]、月塵防護技術和設備的研究[6-7]、月面探測車輛的行走通過特性研究[8]、月塵受外力作用漂浮的二維模擬等方面[9]。

相關的研究方法包括實驗方法和數值模擬方法。由于月面環境的特殊性,且現有月塵珍貴稀少,一般使用特殊研制的模擬月塵來進行實驗。數值模擬的主要方法有有限元法[10]、離散元法[11]等。離散元法是將所分析的物體看作離散顆粒集合體,根據離散物質本身的離散特性,對物質中的每個顆粒作為一個單元建立模型,進行模擬計算。在分析具有離散性質的物質方面離散元法具有較大的優勢。

月球探測器在月面著陸過程中與月塵顆粒發生碰撞作用,導致月塵顆粒揚起。月塵顆粒的運動不僅受探測器的碰撞作用,同時受月塵顆粒之間的碰撞作用。因此月塵顆粒的漂浮受顆粒之間碰撞動力學的控制。本文采用離散元方法,建立月塵幾何模型和接觸力學模型。通過月塵的三軸壓縮實驗來確定月塵的細觀參數。月塵顆粒的漂浮過程可分解為顆粒之間的碰撞過程和顆粒的運動過程。根據所得到的月塵參數建立了三維月塵離散元模擬的計算模型,數值模擬著陸作用下的月塵揚起和漂浮,確定漂浮特性和范圍。

2 月塵三維離散元模型建立和參數確定

2.1 月塵離散元幾何模型的建立

通過掃描電鏡設備獲得的模擬月塵顆粒形態的顯微照片,分析得出模擬月塵顆粒具有復雜的顆粒形態,并以棱角形、次棱角形、長條形、次圓形顆粒形狀為主[13]。

表1 模擬月塵的物理力學性質Table1 Physical and mechanical properties of lunar dust simulant

根據模擬月塵的顆粒形狀特征,采用多球單元重疊法構建單個月塵顆粒的幾何模型。四種顆粒單元的三維幾何模型如圖1所示,每個月塵顆粒是由一個基球O(x0,y0,z)和幾個棱角球Bi(xi,yi,z)(i=1,2,3,…)重疊構成的。圖中R0是基球半徑,R1是顆粒單元外接球半徑。

圖1 四種顆粒單元的幾何模型CAD 圖Fig.1 Geometric models of the four particle unit(CAD)

月塵是覆蓋在月球表面一層厚厚的由于長期環境作用而形成的微小顆粒,顆粒直徑大部分小于1mm,平均直徑為40～130μm[12]。月塵物理力學特性包括顆粒形態、孔隙率、內聚力、內摩擦角、容積密度、顆粒比重等。已知一種模擬月塵的基本物理力學性質[13]如表1所示。

2.2 離散單元接觸力學模型的建立

月塵顆粒是由各種隕石和微隕石撞擊、宇宙射線和太陽風持續不斷轟擊、月表大幅度溫差變化導致月球巖石熱脹冷縮等作用下形成的。因而月塵顆粒間的接觸一般屬于非粘性接觸,月塵整體強度由摩擦強度確定,其表觀粘聚力產生于顆粒間的摩擦和互鎖作用。因此,將顆粒組成的單元的接觸本構模型簡化為彈簧-阻尼線性系統,并引入非張力連接模塊和庫倫摩擦模塊[14],如圖2所示。

兩個單元間接觸作用力Fc可分解為法向作用力Fn和切向作用力Fs

根據圖2,法向接觸作用力Fn由法向彈簧產生的彈性部分Fne和由法向阻尼器產生的非彈性部分Fnd組成。切向作用力Fs包括切向彈性力,切向阻尼力,庫倫摩擦力。

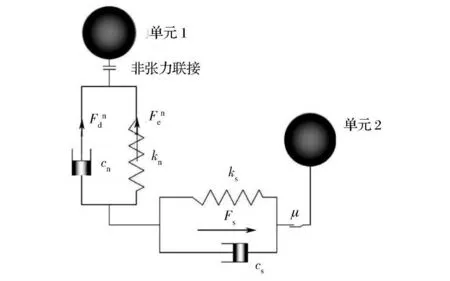
圖2 離散單元接觸力學模型Fig.2 Discrete element contact mechanics model

當顆粒相互接觸時,接觸力可表示為

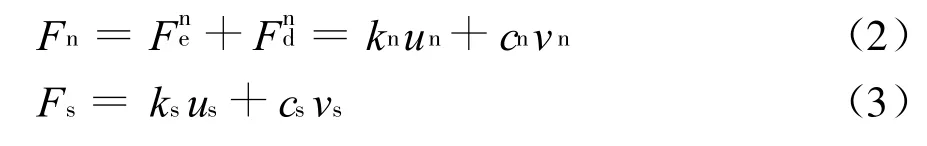
式中kn和ks是法向和切向剛度系數;un和us是顆粒在法向和切向上的位移;cn和cs是法向和切向阻尼系數;vn和vs是接觸時速度在法向和切向上的分量,阻尼力的方向與它們的方向相反。

當接觸單元發生滑動時,由于庫倫摩擦力的存在,切向接觸力不會超過庫倫摩擦力。在模擬計算中,切向作用Fs滿足下列關系

粘性阻尼力與運動方向相反,通常不直接設定阻尼系數,而由粘性阻尼的特征值臨界阻尼比和臨界阻尼常數共同確定,如下式

式中βn和βs分別是法向和切向上的臨界阻尼比。和分別為法向和切向臨界阻尼常數,這兩個常數的計算公式如下

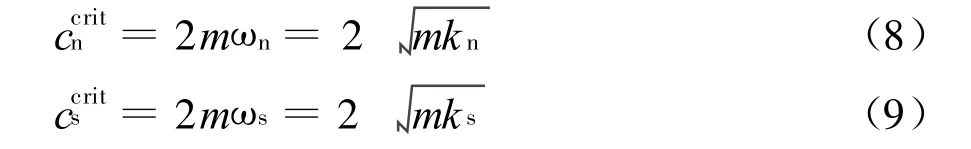
其中,ωn和ωs是無阻尼系統的固有頻率,m是有效系統質量,由所接觸顆粒的質量計算得到

2.3 模擬月塵的細觀參數確定

離散單元模型細觀參數一般無法通過物理實驗直接測量,但是根據相似理論的量綱分析法中的相似第二定理(Π定理),選取月塵宏觀尺度參數楊氏模量E,抗剪強度τmax,容重ρ和細觀尺度參數接觸剛度kn和ks,臨界阻尼比cn和cs,無量綱物理量摩擦系數μ,利用FLT 量綱系統進行分析計算,得到Π關系式

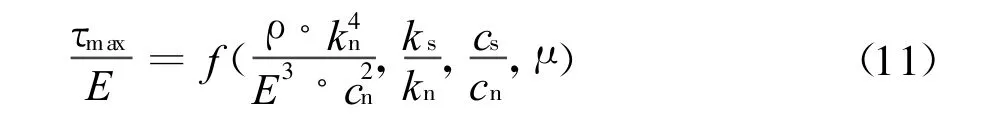
可見月塵的細觀參數與其宏觀力學參數存在尺度定律。可以利用模擬月塵的三軸壓縮實驗結果,采用三維離散元三軸壓縮實驗數值模擬的方法,建立月塵模型細觀參數與宏觀力學屬性的內在聯系,并通過調整輸入參數來確定符合月塵實際宏觀力學特性的最適合離散元模型參數。

2.3.1 三軸壓縮實驗的離散元仿真分析

根據模擬月塵三軸壓縮試樣的實際實驗條件,建立與實際尺寸相同的試樣模型,采用柔性邊界墻維持圍壓和剛性墻加載方式,對試樣的壓縮過程進行模擬。試樣直徑為39mm ,高度H為80mm,三軸壓縮實驗三維離散元仿真模型,如圖3所示,左邊是模型外觀圖,右邊是截面圖。

圖3 三維離散元三軸壓縮實驗仿真模型Fig.3 DEM t riaxial test model

圖中VZ為底部加載墻的加載速度,柔性邊界墻由半徑rb為1mm 的圓球組成的圓環,在80mm高度上分了79層。考慮到壓縮時的變形,組成柔性墻的圓球數中間層中最多,并依層向兩頭遞減。這些圓球相鄰重疊并采用平行粘結的方式相連。為控制邊界條件獲得σ2大小的圍壓,在組成柔性邊界墻的每個圓球上預加力Fb,可由下式近似得到

式中Rb是圓球中心距試樣中心軸的距離,Ni是第i層圓球數。Fb方向從圓球心水平指向Z 軸。

采用底部剛性墻勻速加載和頂部剛性墻應力采集的方法實現三軸壓縮實驗的離散元仿真,試樣受到的主應力差(σ1-σ2)和軸向應變ε可表示為

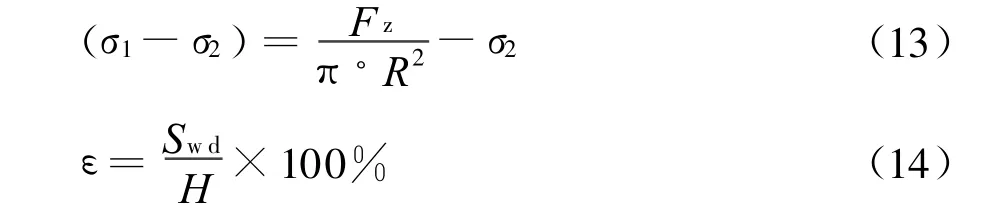
式中σ1為Z 軸方向主應力,Fz是頂部剛性墻受到的Z 方向的不平衡力,R是當前試樣圓柱的平均半徑,Swd是底部剛性墻的垂直位移。

2.3.2 細觀模型參數的確定

根據上述仿真方法,進行了模擬實驗。三軸壓縮實驗仿真試樣的顆粒外接球半徑為1～2.5mm,密度為2 770 kg·m-3,初始孔隙率約為0.35,法向切向臨界阻尼系數為0.7。需要確定的細觀參數是顆粒剛度和摩擦系數。下面分別確定其中一個參數,調整另外一個參數進行試驗。

圖4是圍壓為26kPa,摩擦系數為0.3,顆粒接觸剛度不同時的應力—應變關系曲線。可以看出顆粒單元的剛度越大,則主應力差也越大,峰值越高。隨著剛度的增加,顆粒與壓縮墻體的接觸變得不穩定,接觸力波動逐漸增大,更大的剛度則會致使主應力數值更不穩定。

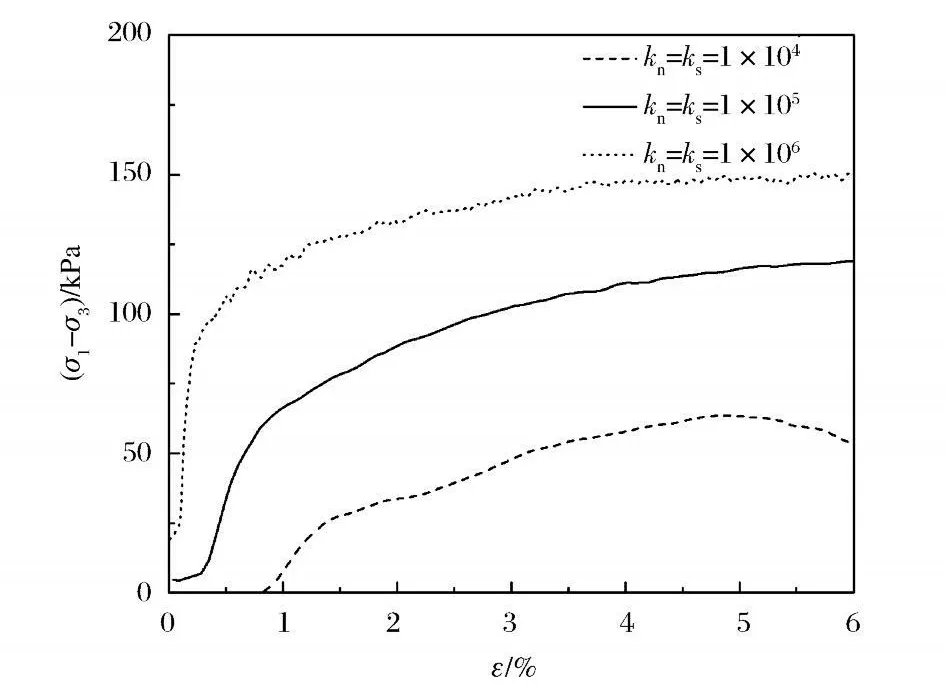
圖4 不同剛度下的應力-應變曲線Fig.4 Axial strain vs.stress curves in different stiffness

圖5 不同摩擦系數下的應力-應變曲線Fig.5 Axial strain vs.stress curves in different friction coefficient

圖5是圍壓為26kPa,法向、切向剛度均為1×105N/m,顆粒間不同摩擦系數下的應力—應變關系曲線。摩擦系數在0.4 以下時,曲線平緩上升,主應力差隨著軸向應變增加而提高,呈現應變硬化。摩擦系數在0.4 以上時,出現了不是非常明顯的峰值強度,即主應力差隨著軸向應變增加而減小,呈現應變軟化,此時顆粒群處于失穩或破壞狀態。可見顆粒摩擦系數越大,則顆粒群在壓縮過程中克服顆粒間的翻轉、滑移所需要的能量越多,在宏觀上體現為主應力差更大。

圖6是用模擬月塵進行的實際三軸壓縮實驗結果[15]。從圖中可以看出隨著軸向應變ε的增大,主應力差(σ1-σ2)也逐漸增大,曲線呈上升趨勢。在應變為4%～5%之間時達到峰值,約為100kPa。之后主應力差隨軸向應變變化不大,曲線趨于平穩,主應力差值在100kPa 左右。

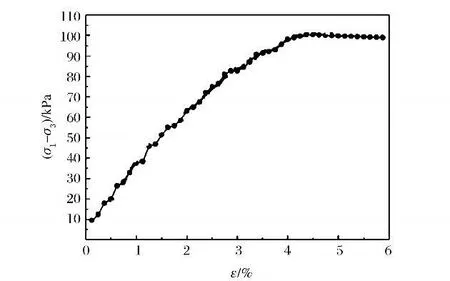
圖6 實際三軸實驗應力-應變曲線Fig.6 Actual axial strain vs.stress curve

根據上述實際實驗結果分析,將仿真模擬得到的結果與之相對比,發現當法向和切向剛度在1×105～5×105N/m、摩擦系數在0.2～0.3 范圍內時曲線趨勢和峰值與實際結果最為相近。將該范圍參數三軸模擬結果與實際結果詳細對比,在應變為4%、主應力差曲線達到峰值時,模擬結果的主應力差值為92～100,而實際實驗主應力差值為97,可見誤差較小,該范圍的參數可以作為仿真試樣模型的參數。

3 著陸作用下月塵漂浮三維模擬

3.1 模擬方法和條件

假設模擬月面著陸器為一圓盤模擬體,并在距離月面一定高度處自由下落。一定數量的月塵顆粒在重力作用下沉降在模擬槽內。圓盤模擬體著陸時與月塵顆粒發生碰撞,使得月塵顆粒的揚起和漂浮。月塵漂浮運動過程滿足顆粒動力學,圓盤模擬體與月塵顆粒以及月塵顆粒間的相互碰撞滿足顆粒碰撞力學。

對圓盤模擬體和月塵顆粒運動情況進行跟蹤,圓盤模擬體和月塵顆粒受微重力作用力和顆粒與圓盤模擬體以及顆粒間碰撞產生的作用力,根據牛頓第二定律,顆粒運動的控制方程為

式中mi、Ⅰi、ui和ωi分別為第i顆粒的質量、慣性距、速度和角速度,Fc為所有與第i顆粒接觸的顆粒對其作用力的合力,Mc為作用在顆粒上的轉矩。

圓盤模擬體和月塵顆粒的接觸力學模型同月塵顆粒間的接觸力學模型,見式(1)、(2)、(3)。根據式(1)和(15),可以確定不同時間顆粒的運動速度和空間位置,統計獲得宏觀顆粒運動特性。

實際月面著陸器和月塵結構非常復雜,為了簡化計算,將月面著陸器簡化成由模擬圓球構成的圓盤模擬體,其質量接近實際著陸器的質量,初始位置定位于月塵表面,初速度按照物體在一定高度自由落體計算。月塵顆粒是按照四種顆粒幾何模型等比組成。月塵分為兩層,上層顆粒細小,受激漂浮。下層顆粒粒徑為上層顆粒三倍,傳遞顆粒間的接觸力。兩層顆粒均在月面重力作用下沉降至平衡,月塵顆粒初始速度為零。模擬計算并統計分析月塵運動特性及月塵空間分布。

3.2 圓盤模擬體著陸和月塵顆粒漂浮過程分析

3.2.1 圓盤模擬體著陸作用下月塵漂浮分析

模擬計算中取圓盤模擬體由一組直徑為0.02m模擬圓球組合構成,其直徑為0.15m,密度為25 000kg/m3。模擬圓球的剛度為1×106N/m,摩擦系數為0.7。月塵顆粒剛度系數為1×105N/m,摩擦系數為0.3,密度為2 770kg/m3。圓盤模擬體和月塵顆粒在微重力條件下碰撞運動,月面重力加速度取為1.68m·s-2。

利用顆粒流程序進行模擬計算時,循環使用的時間步長取臨界時間步長的一部分,取用因子為0.8。在計算循環中顆粒間接觸不斷發生變化,根據上式計算得到的每個循環的時間步長也隨之變化,基本上每個循環均不一樣,這樣就使得每個循環對應的實際時間不相同。在進行數據處理時,根據變化的時間步長來確定實際時間比較麻煩,且不能較為準確地估算得到實際時間,因而這里采用循環步來代替實際時間進行處理。這樣處理直接方便,對最后的結果分析也影響不大。

圖8是月塵顆粒在圓盤模擬體作用下漂浮過程截面圖。初始時圓盤模擬體位于月塵表面,給定初速度V為2m/s。開始計算后,隨著時間的推進,圓盤模擬體在一定初速度和微重力的作用下,與月塵顆粒接觸發生碰撞作用。一部分顆粒被擠壓進月塵內部,隨著擠壓程度增加,月塵內部顆粒密集度增大,抵抗圓盤下落的能力提高,圓盤下落速度減緩。一部分顆粒被揚起,這部分顆粒在圓盤與月塵顆粒發生非彈性碰撞作用時獲得能量,產生向上運動而漂浮。隨著時間推進,漂浮顆粒數增多,顆粒漂浮高度增大。漂浮顆粒在微重力作用下,上升至最高處后開始逐漸回落。

統計分析漂浮月塵顆粒的平均Z 軸向速度Vpaz如圖9所示。初始月塵顆粒靜止,受圓盤著陸碰撞作用,被激揚漂浮,漂浮速度增大,在較短的時間內平均速度達到最大。受微重力作用的影響,月塵顆粒上浮速度不斷減小。隨著計算循環的增加,計算循環到100 000 步時,漂浮顆粒平均速度值為0。此時大部分漂浮顆粒停止上升,漂浮在空中。繼續計算,平均速度變成負值,表明漂浮顆粒大部分開始下落,進入沉降過程,而且下落速度逐漸增大。可見,月塵顆粒的Z 軸向上升速度在受激漂浮后隨著時間的推移逐漸減小。

圖8 圓盤著陸和月塵漂浮過程Fig.8 Progress of simulated disc body landing and luanr dust levitation

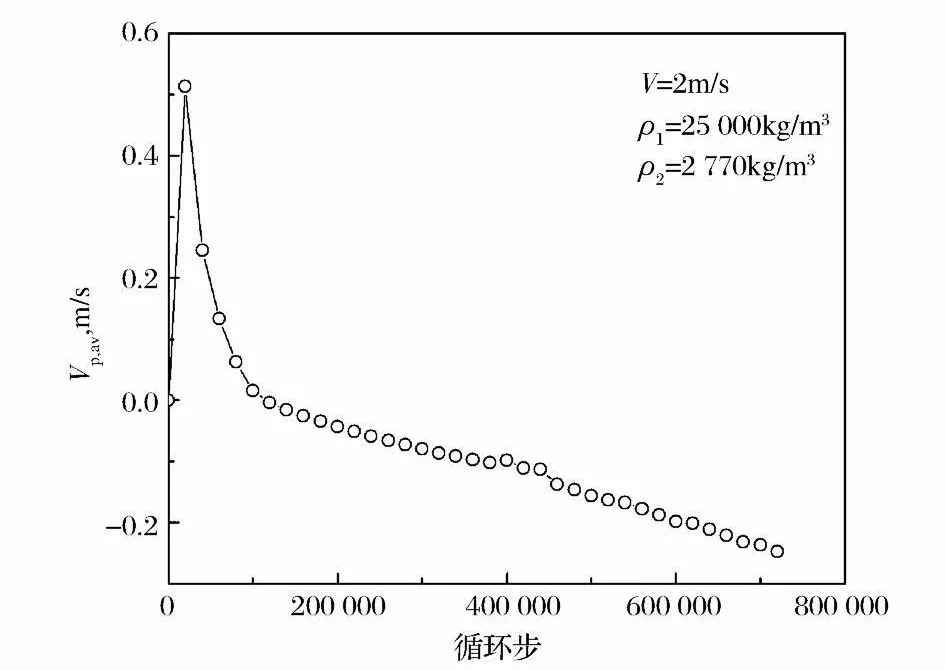
圖9 月塵顆粒平均Z 軸向速度隨時間變化Fig.9 Average Z-axial velocity ofparticles vs.cycle step

圖10 月塵顆粒數沿高度分布Fig.10 Number of particles along the height

圖10是兩個計算步時沿高度h 的月塵顆粒數變化,圖中N是指漂浮的月塵顆粒數。由圖可見沿高度方向漂浮的月塵顆粒數逐漸減少,表明月塵顆粒數在高度上按指數規律遞減。隨著計算循環的繼續,漂浮的月塵顆粒數增多且漂浮高度增加。根據圖中漂浮月塵沿高度上分布情況可以發現,在該計算條件下,月塵漂浮最高可達到70mm。

3.2.2 統計分析著陸速度變化對月塵漂浮的影響

統計在不同著陸速度的圓盤碰撞作用下月塵顆粒漂浮情況,分析圓盤著陸速度對月塵漂浮的影響。圖11是不同著陸速度的圓盤作用下月塵飄浮的最大高度hmax隨時間變化情況。從圖中可以看出,圓盤著陸速度越大,碰撞后月塵漂浮最大高度越大,同時顆粒回落下來的計算時間更長,這表明顆粒漂浮在空中時間變長。且當速度增大時,漂浮高度從近60mm 擴大到近160mm。

圖11 月塵顆粒漂浮最大高度隨時間變化Fig.11 Maximum height of levitation particles changes with time

根據上述分析可以看出,圓盤著陸速度對月塵漂浮數量、漂浮時間和漂浮高度均有影響。且圓盤著陸速度越大,漂浮的月塵顆粒數越多,漂浮時間越長,漂浮高度越高。在以上三種著陸速度條件下的計算結果表明,漂浮最大高度能夠達到近160mm。

著陸速度的變化除了沿豎直方向上的量值變化,還存在偏離豎直方向從而帶有切向速度分量的情況。這里簡單研究了速度為2m/s,水平方向上有速度分量,即速度的方向沿X 軸偏離豎直方向15°和30°時這兩種條件下對月塵受激漂浮的影響。圖12為速度是2m/s 偏離角度α是15°和30°時,月塵顆粒漂浮數沿高度分布情況。

圖12 中明顯看出偏離角度較小時,豎直方向上的速度分量較大,月塵漂浮的顆粒數也相應較大,大于飄離角度大時(即豎直方向上的速度分量較小時)的數量,這顯然與之前獲得的豎直方向上速度量的變化引起的月塵漂浮顆粒數變化相一致。而兩種情況下的月塵漂浮最大高度相差不大,這是因為在模擬計算過程中,月塵顆粒受激漂浮時在飛揚過程中顆粒間也會相互碰撞,使得原本漂浮高度較小的獲得飄向更大高度的能量,使得最大漂浮高度上升,因而最大漂浮高度相差不大。

3.2.3 統計分析月塵細觀參數變化對月塵漂浮的影響

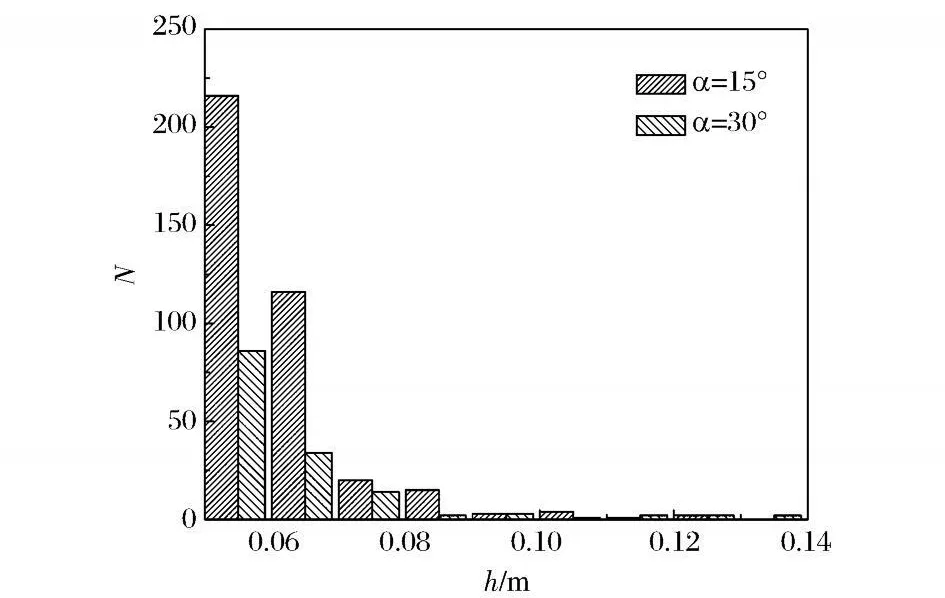
圖12 月塵漂浮顆粒數沿高度分布Fig.12 Number of particles along the height

統計月塵顆粒其細觀參數中顆粒剛度變化時月塵漂浮的情況。在上述確定的最合適月塵剛度范圍內,即1×105～5×105N/m,取值進行計算模擬。分析月塵顆粒剛度分別為1×105N/m、2.5×105N/m和5×105N/m時,圓盤以2m/s 的速度著陸,月塵受激揚的漂浮情況。圖13是月塵顆粒不同剛度時漂浮最大高度隨時間變化情況。

圖13 月塵顆粒漂浮最大高度隨時間變化Fig.13 Maximum height of levitation particles changes with time

從圖13可以發現,月塵顆粒細觀參數中剛度變化時,月塵顆粒漂浮受到影響。剛度越大,顆粒間相同變形所需的接觸力增大,月塵顆粒漂浮上揚需要的能量增大。因而相同條件下月塵顆粒剛度大則揚起的最大高度小,剛度小反而揚起的最大高度大。同時對月塵顆粒漂浮的時間也有影響,剛度較大時,漂浮的時間較短;剛度較小時,漂浮的時間較長。統計分析三種剛度情況下月塵顆粒漂浮達到最大高度時的漂浮顆粒數,發現漂浮顆粒數量的變化不大。這表明剛度變化對月塵漂浮的最大高度和漂浮時間有一定影響,而對漂浮顆粒數影響不大。

4 結論

著陸器在月球表面進行著陸操作時,會引起月面月塵顆粒的激揚行為,并且這種激揚特性與月塵顆粒的宏細觀物理力學屬性、著陸器的結構特征及其工作參數等因素密切相關。

采用一種三維離散元計算機仿真方法來模擬著陸過程中的月塵激揚問題。通過三維三軸壓縮實驗仿真的方法,對比模擬結果和實際結果得到最適合的月塵模擬參數。利用圓盤模擬體-月塵的離散元三維分析模型,進行了圓盤著陸碰撞作用下月塵漂浮過程模擬。

對圓盤模擬體著陸時引起的月塵浮揚情況進行了統計分析,得出漂浮的月塵先隨時間增加而增多,然后在微重力作用下逐漸回落。漂浮的月塵顆粒數沿高度按指數規律遞減。在給定其他計算條件下,圓盤初速度為2m/s時,月塵漂浮高度范圍為70mm。統計分析了著陸速度和月塵顆粒剛度的變化對月塵漂浮的影響。圓盤著陸速度變化對月塵漂浮的數量、時間和高度的影響較大,且隨著陸速度的增大,月塵漂浮的數量、時間和高度的值也增大。當著陸速度在3m/s時,月塵漂浮高度范圍可達160mm。當存在水平速度分量時,水平速度分量增大,揚起的月塵顆粒數明顯減少。月塵顆粒剛度變化對月塵顆粒漂浮的高度和時間有影響。剛度越大時,月塵顆粒漂浮的最大高度和漂浮時間越小,但是剛度變化對月塵漂浮顆粒數影響不大,三種剛度下漂浮的月塵顆粒數相近。

References)

[1]Gaier J R.The effects of lunar dust on EVAsystem s during the Apollo missions [R].NASA/TM-2005-213610,2005

[2]David W C III.Lunar soil grain size dist ribution[J].Planetary and Earth Sciences Division,1972,10

[3]Park J S,Liu Y,Kihm K D,et al.Micro-morphology and toxicological effects of lunar dust[J].Lunar and Planetary Science,2006,XXXVII

[4]Walton O R.Adhesion of lunar dust[R],NASA/CR-2007-214685,2007

[5]Mazumder M K,Horenstein M N,Trigw ell S,et al.Electrostatic and gravitational transport of lunar dust in the airless atmosphere of the moon[J].IEEE 978-1-4244-2279-1/08,2008

[6]Calle C I,Buhler C R,McFall J L,et al.Particle removal by electrostatic and dielectrophoretic forces for dust control during lunar exploration missions [J].Journal of electrostatics,2009,67:89-92

[7]Clark P E,Curtis S A,Minetto F A,et al.Characterizing physical and electrostatic properties of lunar dust as a basis for developing dust removal tools[C]// NLSI Lunar Science Conference,2008

[8]鄒猛,李建橋,張金換,等.月球車驅動輪牽引性能研究[J].宇航學報,2009,1:98-103

[9]王淑彥,何玉榮,劉國棟,等.二維拱形模擬體作用下月塵顆粒懸浮過程研究[C]//大慶:2007 多相流學術會議,中國工程熱物理學會,2007

[10]David W C III.Lunar soil mechanics:distribution of contact stress beneath a rigid plate resting on sand[D].Massachusetss Institute of Technology,1968

[11]Koji Wada,H iroki Senshu,Takafumi Matsui.Numerical simulation of impact cratering on granular material[J].Icarus 2006,180:528-545

[12]鄭永春,歐陽自遠.月壤的物理和機械性質[J].礦物巖石,2004,24(4):14-19

[13]Li Wen,Gao Feng,Jia Yang,Tractive performance analysis on radially deployable wheel configuration of lunar rover vehicle by discrete element method[J].Chinese Journal of Mechanical Engineering 2008,21(4):66-72

[14]Li Wen,Huang Yong,Cui Yi,et al.Trafficability analysis of lunar mare terrain by means of the discrete element method for w heeled rover locomotion[J].Journal of Terramechanics,2010,47(3):161-172

[15]高峰,李雯,孫剛,等.模擬月壤可行駛性的離散元數值分析[J].北京航空航天大學學報,2009,35(4):501-504