古斯—漢欣位移的自發(fā)輻射量子相干調(diào)控

鄧文武，孫利輝

（1.華中師范大學(xué) 物理科學(xué)與技術(shù)學(xué)院，武漢 430079；2.咸寧學(xué)院 光子學(xué)與光子技術(shù)研究所，湖北 咸寧 437005）

1947 年，F(xiàn)ritz Goos 和 Hilda Lindberg－H?nchen兩位物理學(xué)家發(fā)現(xiàn)，光束在兩種介質(zhì)界面上發(fā)生全反射時(shí)，反射點(diǎn)相對(duì)于入射點(diǎn)在相位上有一突變，而反射光相對(duì)于入射光在空間上有一段距離，這一距離被稱為古斯－漢欣（GH）位移［1－2］.由于古斯－漢欣位移深刻的物理內(nèi)涵，自發(fā)現(xiàn)以來，備受物理界的關(guān)注.人們已采用了相位法［3］、能量守恒［4］等不同的理論成功地解釋了這種現(xiàn)象.同時(shí)，由于古斯－漢欣位移在集成光學(xué)、光波導(dǎo)開關(guān)、光學(xué)傳感器、量子力學(xué)、等離子物理、信息傳輸?shù)确矫嬗兄浅Ｖ匾摹撛诘膽?yīng)用，一直是研究的熱點(diǎn).早期，古斯－漢欣位移研究的熱點(diǎn)主要集中在選用不同種類、不同結(jié)構(gòu)的介質(zhì)來實(shí)現(xiàn)負(fù)、正位移的增強(qiáng)，例如：弱吸收介質(zhì)［5－6］、光子晶體［7－8］、負(fù)折射材料［9］等.然而，這些研究都是通過改變介質(zhì)的結(jié)構(gòu)或種類來實(shí)現(xiàn)的.對(duì)于一個(gè)固定的結(jié)構(gòu)或種類，古斯－漢欣位移不易于操控.

最近，Scully［10］提出了一個(gè)在腔中利用外加強(qiáng)驅(qū)動(dòng)場(chǎng)來實(shí)現(xiàn)零吸收，同時(shí)得到最大折射率的方案.基于此方案的思路，各種不同的、利用外加強(qiáng)驅(qū)動(dòng)場(chǎng)來改變介質(zhì)色散—吸收性質(zhì)從而達(dá)到調(diào)控、增強(qiáng)古斯－漢欣位移的方案被提出，從而使古斯－漢欣位移的研究進(jìn)一步地?zé)崞饋?這些方案與以前的方案顯著的不同點(diǎn)在于通過外加驅(qū)動(dòng)場(chǎng)來直接調(diào)控古斯－漢欣位移，在實(shí)際的應(yīng)用中具有更好的操作性.例如：Wang［11］等人考察了腔中二能級(jí)原子，通過改變外加驅(qū)動(dòng)場(chǎng)的強(qiáng)度和場(chǎng)與原子的失諧量來成功實(shí)現(xiàn)了很大的負(fù)向和正向位移；隨后Ziauddin［12］等人又分析了腔中三能級(jí)和四能級(jí)原子的古斯－漢欣位移，發(fā)現(xiàn)三能級(jí)電磁感應(yīng)透明（EIT）結(jié)構(gòu)中對(duì)超光速傳導(dǎo)波存在強(qiáng)的吸收，對(duì)出現(xiàn)大的位移不利，而采用四能級(jí)原子克服了這一不利因素.

事實(shí)上腔中原子介質(zhì)的光學(xué)性質(zhì)除了與外加驅(qū)動(dòng)場(chǎng)有關(guān)外，還與原子本身的結(jié)構(gòu)和自發(fā)輻射等因素有關(guān)，而對(duì)于自發(fā)輻射中的量子相干（SGC）對(duì)古斯－漢欣位移的影響還未見報(bào)道.本文是基于Scully的思想，討論了腔中四能級(jí)外加驅(qū)動(dòng)場(chǎng)對(duì)古斯－漢欣位移的影響，特別是自發(fā)輻射中的量子相干對(duì)古斯－漢欣位移的影響.研究表明自發(fā)輻射中的量子相干對(duì)古斯－漢欣位移的影響較大，對(duì)古斯－漢欣位移起抑制或加強(qiáng)的作用.

1 理論模型

如圖1（a）所示，頻率為ωp的弱TE探測(cè)場(chǎng)從真空中以θ角入射到腔中，腔由厚度為d1、d3非電磁極板組成，介電常數(shù)為ε1；腔內(nèi)的四能級(jí)原子介質(zhì)厚度為d2，原子結(jié)構(gòu)如圖1（b）所示.弱探測(cè)場(chǎng)分別與能級(jí)｜1〉和兩個(gè)近能級(jí)｜2〉、｜3〉耦合，拉比頻率分別為Ωp1、Ωp2；同時(shí)，頻率為ωT的外加驅(qū)動(dòng)場(chǎng)分別與能級(jí)｜4〉和近能級(jí)｜2〉、｜3〉耦合，對(duì)應(yīng)的拉比頻率分別為ΩT1、ΩT2；Γ4、Γ3、Γ2分別為對(duì)應(yīng)能級(jí)的衰減系數(shù)，ωp、ωT與原子的本征頻率滿足：Δp＝－ωp＋ （ω21＋ ω23）／2、ΔT＝－ ωT＋ （ω42＋ω43）／2，如圖1（b）所示.為討論方便，假定Ωp1＝Ωp2＝Ωp、ΩT1＝ΩT2＝ΩT.

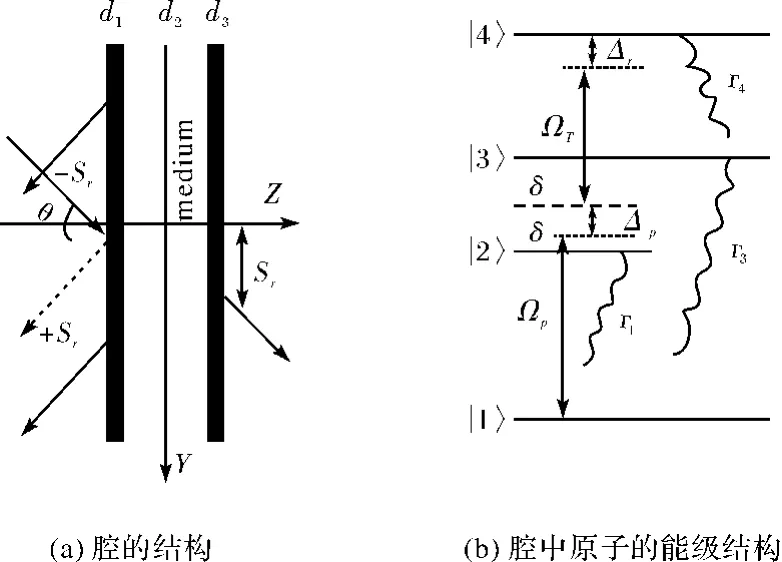
圖1 理論模型Fig.1 The theory model

假定體系在任意時(shí)刻的態(tài)函數(shù)為｜ψ（t）〉＝c4（t）｜4〉＋c3（t）｜3〉＋c2（t）｜2〉＋c1（t）｜1〉，在偶極和旋波近似下，運(yùn)用 Weisskopf－Wigner理論及旋轉(zhuǎn)變換坐標(biāo)系中的薛定諤方程，容易得到原子各個(gè)能態(tài)幾率幅隨時(shí)間的演化方程滿足（?＝1）［13］：式中，r2＝Δp－δ＋iΓ2／2、r3＝Δp＋δ＋iΓ3／2、r4＝Δp＋ΔT＋iΓ4／2；μ ＝η（式中η＝cosα）表征近能級(jí)｜2〉和｜3〉交叉耦合所對(duì)應(yīng)的自發(fā)輻射量子相干.

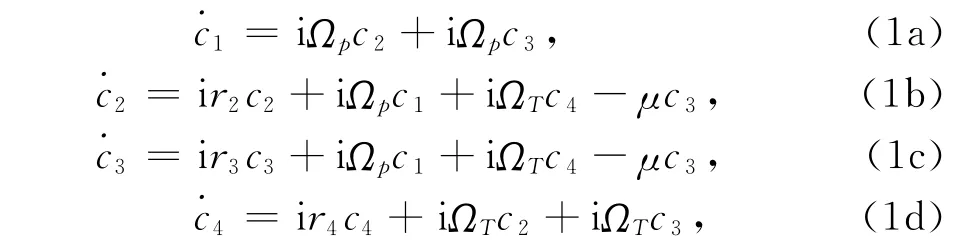
考慮弱探測(cè)場(chǎng)近似，那么原子幾乎始終在基態(tài)｜1〉上，即｜c(diǎn)1｜2≈1容易得到（1）式在穩(wěn)態(tài)情況下的解.利用原子的極化率公式Pp＝ε0χpEp＝2 N（），容易得到在探測(cè)場(chǎng)作用下原子介質(zhì)的極化率：

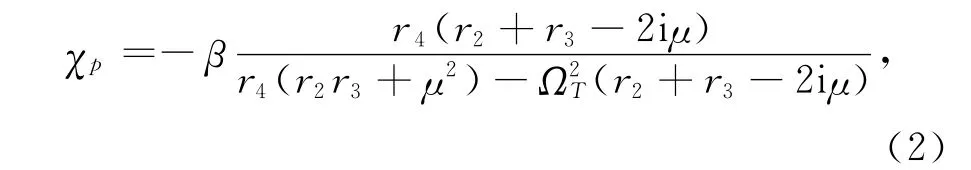
式中，β＝Nξ2，N、ξ分別代表原子的密度和偶極躍遷矩陣元.

2 古斯 －漢欣位移及其數(shù)值分析

根據(jù)光在介質(zhì)中的特征傳播矩陣，探測(cè)場(chǎng)在第層介質(zhì)中的傳播矩陣為［14］：

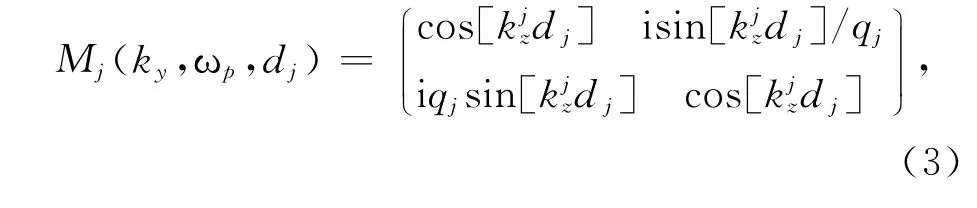
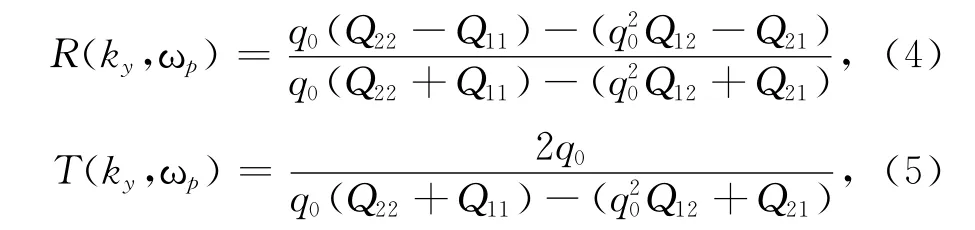
式中，q0＝kz／k，Qij為總的傳播矩陣Q的矩陣元.

同時(shí)根據(jù)穩(wěn)態(tài)相位理論［3，15］，得到反射光和透射光的古斯－漢欣位移分別為：

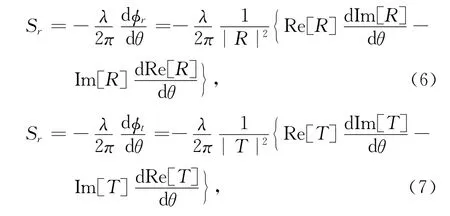
式中，φr、φt分別表示反射系數(shù)和透射系數(shù)的相位.

從（6）式及（7）式中可以看出古斯－漢欣位移與原子介質(zhì)的線性極化率χp、厚度d2、極板厚度d1（d3）、介電常數(shù)等密切相關(guān).在這里主要討論自發(fā)輻射量子相干及外加激發(fā)場(chǎng)對(duì)古斯－漢欣位移的影響.為了討論的方便，假定d1＝d3＝0.2μm、d2＝5μm、ε1＝ε3＝2.22、ωp＝2π×300THZ.

圖2為在不同的α下，所對(duì)應(yīng)的自發(fā)輻射量子相干程度不同的情況下對(duì)古斯—漢欣位移的影響.從圖中可以看出當(dāng)α＝0時(shí)，即近能級(jí)｜2〉和｜3〉交叉耦合所對(duì)應(yīng)的自發(fā)輻射量子相干μ＝，此時(shí)能級(jí)｜1〉｜3〉、｜1〉｜2〉的偶極距矢量方向相同，反射光（Sr）和透射光（St）的古斯—漢欣位移相對(duì)較小，對(duì)古斯 －漢欣位移起抑制作用；當(dāng)α＝π／2時(shí)，此時(shí)能級(jí)｜1〉｜3〉、｜1〉｜2〉的偶極距矢量方向正交，自發(fā)輻射量子相干消失，反射光（Sr）和透射光（St）的古斯－漢欣位移也相對(duì)較小；而當(dāng)α＝π時(shí)，反射光（Sr）和透射光（St）的古斯 －漢欣位移明顯地得到加強(qiáng)和提高，此時(shí)能級(jí)｜1〉｜3〉、｜1〉｜2〉的偶極距矢量方向剛好相反，自發(fā)輻射量子相干對(duì)古斯—漢欣位移起加強(qiáng)作用.通過對(duì)圖2的分析，近能級(jí)｜2〉和｜3〉交叉耦合所對(duì)應(yīng)的自發(fā)輻射量子相干對(duì)古斯—漢欣位移影響較大，對(duì)古斯—漢欣位移起抑制或加強(qiáng)的作用.從圖2也可以看出：透射光（St）的古斯—漢欣位移比反射光（Sr）要大，當(dāng)α＝π時(shí)，透射光和反射光的古斯—漢欣位移的峰值同時(shí)達(dá)到最大，位移的方向剛好相反，可以實(shí)現(xiàn)較大的負(fù)或正古斯—漢欣位移，如圖2（c）所示.

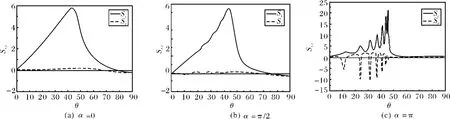
圖2 古斯—漢欣位移在不同α下隨入射角θ的演化規(guī)律Г2＝Г3＝Г4＝γ，δ＝γ，ΩT＝2γ，ΔT＝－25γ，ΔP＝4γFig.2 The dependence of the GH shifts of the transmitted（solid curves）and reflected（dashed curves）beams on the incidence angle（θ）with different

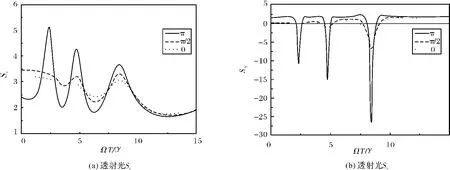
圖3 古斯—漢欣位移在不同α下隨激發(fā)場(chǎng)強(qiáng)度ΩT／γ的演化規(guī)律θ＝25°，其它參數(shù)同圖2Fig.3 The dependence of the GH shifts of the transmitted and reflected beams on the strengths（ΩT／γ）of control beam with different

為了進(jìn)一步的分析自發(fā)輻射量子相干對(duì)古斯—漢欣位移影響，我們研究了在固定的入射角θ＝25°的情況下反射光和透射光的古斯—漢欣位移隨外加驅(qū)動(dòng)場(chǎng)的演化規(guī)律，如圖3所示.圖3（a）為透射光的古斯 —漢欣位移，圖3（b）對(duì)應(yīng)反射光古斯—漢欣位移.分別討論了在θ＝25°情況下的α＝0、α＝π／2、α＝π.通過對(duì)比發(fā)現(xiàn)自發(fā)輻射量子相干同樣對(duì)古斯—漢欣位移起抑制或加強(qiáng)的作用，并且抑制或加強(qiáng)的程度與外加驅(qū)動(dòng)場(chǎng)的強(qiáng)度密切相關(guān).因此對(duì)古斯—漢欣位移的調(diào)控我們?cè)诳紤]自發(fā)輻射量子相干的同時(shí)，也必需考慮外加驅(qū)動(dòng)場(chǎng)的強(qiáng)度對(duì)古斯—漢欣位移影響，并且在α＝π時(shí)，外加驅(qū)動(dòng)場(chǎng)的強(qiáng)度對(duì)反射光和透射光的古斯—漢欣位移調(diào)控最為明顯.

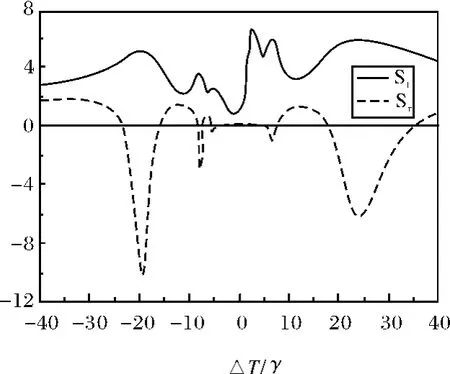
圖4 古斯—漢欣位移隨ΔT／γ的演化規(guī)律α＝π，θ＝25°，其它參數(shù)同圖2Fig.4 The dependence of the GH shifts of the transmitted and reflected beams on the detuning（ΔT／γ）

通過圖2和圖3的分析可知在α＝π時(shí)自發(fā)輻射量子相干對(duì)反射光和透射光的古斯—漢欣位移起加強(qiáng)作用，因此，圖4分析了在α＝π時(shí)外加驅(qū)動(dòng)場(chǎng)與原子的失諧量對(duì)古斯—漢欣位移影響，實(shí)線反映透射光的古斯—漢欣位移，虛線對(duì)應(yīng)反射光的古斯—漢欣位移.從圖4可知在時(shí)古斯—漢欣位移受外加驅(qū)動(dòng)場(chǎng)與原子的失諧量的調(diào)控影響較大，透射光和反射光的古斯—漢欣位移的峰值同時(shí)達(dá)到最大，位移的方向剛好相反.

3 結(jié) 論

本文通過穩(wěn)態(tài)相位理論對(duì)固定結(jié)構(gòu)光腔中原子介質(zhì)的古斯－漢欣位移進(jìn)行了討論.通過外加強(qiáng)驅(qū)動(dòng)場(chǎng)的調(diào)控，同時(shí)考慮原子介質(zhì)自發(fā)輻射量子相干，從而使探測(cè)光的古斯－漢欣位移也發(fā)生了極大的變化，與傳統(tǒng)的古斯－漢欣調(diào)控相比，通過此方法不需要改變體系的物理結(jié)構(gòu).分析得出：通過對(duì)外加驅(qū)動(dòng)場(chǎng)強(qiáng)度、失諧的調(diào)控，更易于操控古斯—漢欣位移；同時(shí)發(fā)現(xiàn)原子介質(zhì)的自發(fā)輻射量子相干對(duì)古斯－漢欣位移的影響較大，在α＝π的一定自發(fā)輻射量子相干下，外加驅(qū)動(dòng)場(chǎng)的強(qiáng)度和失諧對(duì)反射光和透射光的古斯—漢欣位移調(diào)控最為明顯，可以實(shí)現(xiàn)大的古斯－漢欣位移.

［1］Goos F，H?nchen H.Ein neuer and fundamentaler Versuch zur Totalreflexion［J］.Ann Phys，1947，1（6）：333（1－4）.

［2］Goos F，H?nchen H.Neumessang des Strahlversetzungeffkets bei Totalreflexion［J］.Ann Phys，1949，5（3）：251（1－3）.

［3］Artmann K.Berechnung der seitenversetzung des totalre flektierten strahles［J］.Ann Phys，1948，437：87（1－15）.

［4］Steinberg A M，Chiao R Y.Tunneling delay times in one and two dimensions［J］.Phys Rev A，1994，49：3283（1－6）.

［5］Lai H M，Chan S W.Large and negative Goos– H?nchen shift near the brewster dip on reflction from weakly absorbing media［J］.Opt Lett，2002，27：680（1－5）.

［6］Wang L G，Chen H，Zhu S Y.Large negative Goos–H?nchen shift from a weakly absorbing dielectric slab［J］.Opt Lett，2005，30：2936（1－3）.

［7］Felbacq D，Moreau A，Smaali R.Goos– H?nchen effect in the gaps of photonic crystals［J］.Opt Lett，2003，28：1633（1－3）.

［8］Wang L G，Zhu S Y.Giant lateral shift of a light beam at the defect mode in one－dimensional photonic crystals［J］.Opt Lett，2006，31：101（1－5）.

［9］Berman P R.Goos－H?nchen shift in negatively refractive media［J］.Phys Rev E 2002，66：067603（1－3）.

［10］Scully M O.Enhancement of the index of refraction via quantum coherence［J］.Phys Rev Lett，2002，67：1855（1－5）.

［11］Wang L G，M.Ikram，Zubairy M S.Control of the Goos－H?nchen shift of a light beam via a coherent driving field［J］.Phys Rev A，2008，77：023811（1－6）.

［12］Ziauddin，Q S，Zubairy M S.Coherent control of the Goos－H?nchen shift［J］.Phys Rev A，2007，81：023821（1－10）.

［13］Wan Ren－Gang，Kou Jun，Jiang Li，et al.Electromagnetically induced grating via enhanced nonlinear modulation by spontaneously generated coherence［J］.Phys Rev A，2011，83：033824（1－8）.

［14］趙建林.高等光學(xué)［M］.北京：國(guó)防工業(yè)出版社，2003.

［15］Born M，Wolf E.Principles of Optics［M］.Cambridge：Cambridge University Press，1999.