WRF-EnSRF系統同化多普勒雷達資料在多類型強對流天氣過程的數值試驗

陳杰，閔錦忠，王世璋，王孝慈

(1.94701部隊，安徽安慶246001;2.南京信息工程大學氣象災害省部共建教育部重點實驗室，江蘇南京210044)

WRF-EnSRF系統同化多普勒雷達資料在多類型強對流天氣過程的數值試驗

陳杰1，2，閔錦忠2，王世璋2，王孝慈2

(1.94701部隊，安徽安慶246001;2.南京信息工程大學氣象災害省部共建教育部重點實驗室，江蘇南京210044)

利用自主構建的基于風暴尺度的WRF-EnSRF(weather research and forecasting ensemble square root filter)系統同化實際多普勒雷達資料，檢驗該同化系統在包括颮線、超級單體風暴和多單體風暴3個不同結構類型的強對流天氣過程的同化效果，并考察了初始場擾動時不同強度的位溫和水汽擾動對集合離散度以及同化效果的影響。結果表明，在3個個例中該同化系統均表現出有效的同化能力，各分析結果均比較合理，徑向速度和反射率因子分析的增量均方差在經過24 min同化后分別下降到3～5 m/s和10 dBz，并維持至60 min同化結束。預報場集合離散度和同化效果對熱力場的擾動強度比較敏感，適當增加初始擾動時位溫和水汽的擾動強度有利于提高集合離散度和改善徑向速度的分析效果。

EnSRF;風暴尺度;多普勒雷達資料

0 引言

風暴尺度數值預報對于強對流天氣系統三維風場與熱力場的模擬和重建一直是大氣科學中難以解決的難題。多普勒天氣雷達幾乎是能夠探測到風暴尺度系統三維信息的唯一工具，因此很多研究集中于雷達資料的反演和同化上(Sun and Crook，1997，1998)。本文利用基于WRF(weather research and forecasting)模式開發的集合平方根濾波(ensemble square root filter，EnSRF)同化系統，對3個不同結構類型的強對流天氣過程進行多普勒雷達資料同化。

Evensen(1994)首次把集合卡爾曼濾波(ensemble Kalman filter，EnKF)應用到海洋同化領域中，EnKF是一個用蒙特卡羅的短期集合預報方法來估計預報誤差協方差的四維同化方法。Houtekamer and Mitchell(1998)把EnKF引入到大氣資料同化系統，并進行了一系列研究。Snyder and Zhang(2003)驗證了EnKF應用于風暴尺度同化的潛力。EnKF可以通過一組有限集合成員統計出具有流依賴性質的背景誤差協方差，并且不需要預報模式的切線性模式和伴隨模式，可以和模式相互獨立，易于移植和維護，越來越受到人們的重視。目前針對EnKF的研究主要集中于模擬雷達資料同化上(Snyder and Zhang，2003;Zhang et al.，2004;Tong and Xue，2005;Xue et al.，2006)。Tong and Xue(2005)在ARPS模式上構建了EnKF系統并進行模擬雷達同化試驗，結果表明，通過聯合同化反射率因子和徑向速度，風暴系統結構可以很好的重建。許小永等(2006)利用EnKF在云模式中同化模擬雷達觀測，并考察了不同條件下的同化效果。蘭偉仁等(2010a，2010b)也利用一次風暴過程的模擬多普勒雷達資料進行一系列敏感性試驗，并且探討了EnKF在有顯著模式誤差的情況下同化模擬多普勒雷達資料的效果問題。針對實際雷達資料的EnKF研究還比較少，早期Dowell et al.(2004)用EnKF同化了實際的雷達觀測資料。Tong(2006)在龍卷雷暴個例中應用了EnKF同化實際雷達資料，對比了同化單雷達資料與雙雷達資料的效果。Aksoy et al.(2009)利用DART系統(Anderson and Collins，2007)在三類風暴尺度天氣過程中同化實際雷達資料，考察了系統在各類型個例中的同化性能。

由于EnSRF能夠避免傳統的EnKF中由于觀測擾動帶來的采樣誤差而導致的分析誤差協方差低估的問題(Whitaker and Hamill，2002)，因此，本文在WRF模式上構建WRF-EnSRF同化系統，并利用該系統在3個不同類型(颮線、超級單體風暴和多單體風暴)的獨立的強對流天氣過程中同化多普勒雷達資料，進而考察系統在風暴尺度的同化性能。

對流風暴是大氣中不穩定能量釋放的產物，它的發生發展與其環境的熱力結構必然有密切聯系。在EnKF的研究中，預報場的集合離散度不足是一個普遍的問題(Aksoy et al.，2009)。因此，考慮到初始場中熱力場的不確定性與預報場的集合離散度應該有密切關系，本文考察了初始場擾動時不同強度的位溫和水汽擾動對集合離散度以及同化效果的影響。

1 個例簡介和資料

1.1 個例介紹

選取風暴尺度天氣中具有代表性的3個不同類型的強對流天氣過程，包括2009年6月14日颮線，2008年6月3日超級單體風暴和2005年4月20日多單體風暴。該3個個例的共同特點是:南京雷達站的多普勒雷達可以較好地探測它們的發生發展過程，雷達資料方便獲取;其次是系統發生發展的區域地形比較平坦，一致性較好。

2009年6月14日颮線主要成因是:東北冷渦活動頻繁且強度偏強，有利于引導強冷空氣南下，使得豫皖蘇地區上干冷下暖濕的不穩定條件逐漸形成。同時由于中高層干冷空氣的侵入(干冷平流)和底層暖濕平流的共同作用，使得不穩定能量聚集，進一步增強層結的不穩定性。6月14日颮線主要襲擊安徽、江蘇等地，都有冰雹、大風、雷電、短時強降水等天氣現象，造成多人傷亡，直接經濟損失嚴重。

2008年6月3日安徽江北地區受多個雷暴單體影響，09:00(世界時，下同)左右滁州地區對流系統呈現明顯的超級單體特征(周昆等，2008)。這次強對流天氣是在高空東北冷渦后部弱冷空氣擴散南下以及地面冷鋒東移南下共同作用下發生的。安徽江北地區有冰雹、雷電、大風等災害天氣，造成了嚴重災害。

2005年4月20日江蘇中部地區發生一次強對流天氣過程，造成此次強對流天氣的3個風暴群，分別從安徽的宿州和江蘇宿遷的沭陽、淮陰的泗陽生成，沿三條路徑向東南方向移動，并逐步加強發展、演變成多單體風暴(謝義明等，2008)。此次強對流天氣主要由東北冷渦南壓造成，并有高、低空三支急流的耦合為其提供動力上升條件。江蘇中部地區遭受了大風、冰雹、龍卷的襲擊，造成了嚴重的財產損失和人員傷亡。

1.2 資料介紹及處理

背景場及邊界條件采用NCEP/NCAR的1°×1°分析資料，各風暴個例雷達資料均采用南京站多普勒雷達資料，颮線、超級單體風暴和多單體風暴的雷達資料時段分別是2009年6月14日09:00—10:30、2008年6月3日08:00—09:30、2005年4月20日08:00—09:30。南京站多普勒雷達是我國新一代S波段多普勒天氣雷達(CINRAD/SA)，反射率因子距離庫長為1 000 m，最大距離庫數為460;徑向速度和譜寬距離庫長為250 m，最大距離庫數為920，約6 min一次體掃。

由于雷達硬件設備的限制，雷達資料在強風條件下會出現速度模糊的現象。此外，由于大氣湍流、地物雜波等對雷達探測的干擾，使得雷達資料存在很大的觀測噪音。在雷達資料同化過程中，雷達資料的質量控制是非常重要的一步，本文雷達資料預處理主要包括:

1)去噪聲。由于近地面湍流，地物雜波等影響，去除小于1 km以下的資料;又由于本文關注強對流天氣，因此在雷達反射率因子資料中剔除反射率因子小于10 dBz的非降水回波。

2)退模糊。采用基于模式背景場和雷達探測徑向速度的差值退速度模糊的方法(陳力強等，2009)。若背景場徑向速度和雷達探測徑向速度的差值的絕對值超過30 m/s，則剔除該徑向速度資料。

3)數據粗化。雷達資料具有高時空分辨率，如果將所有觀測資料放入同化系統中，不但會增加計算負擔，而且由于觀測間存在一定的相關性，使得分析結果并不理想(潘敖大等，2009)。因此，利用數據粗化方法將雷達資料進行處理。本文在錐面上采用格點周圍最近的四個點資料進行雙線性插值，將雷達資料插值到格點所在位置。粗化后資料仍位于錐面上，水平分辨率為5 km。

4)數據填補。由于原始資料經常存在缺測，且粗化后的資料過于稀疏，因此對資料進行適當的填補可以改善同化效果(閔錦忠等，2007)。本文在錐面上進行2維BARNUS插值。如果缺測點周圍一圈有超過半數格點有效，則用周圍一圈數據處理，如果缺測點周圍兩圈有超過半數格點有效，則用周圍兩圈數據處理。

2 預報模式和EnSRF

2.1 WRF模式

應用一個完全可壓縮、非靜力中尺度模式WRFV2.2.1的ARW版本作為系統的預報模式。該模式水平方向采用荒川C網格，垂直方向采用隨地形的質量坐標。在同化試驗中，模式水平區域格點為200×200，水平格距5 km，垂直方向采用系統默認的28層。微物理方案采用相對復雜的lin方案，由于分辨率較高，不使用積云參數化方案。

2.2 EnSRF算法

在集合成員數有限的情況下，觀測加擾動會引入樣本誤差，從而影響誤差協方差的正確估計，并可能引起濾波發散。因而，觀測不加擾動的EnKF方法(即集合平方根濾波，EnSRF)被提出(Whitaker and Hamill，2002)。EnSRF算法是在假設觀測誤差不相關時以順序同化方式同化觀測，即一次同化一個觀測。因此觀測誤差協方差矩陣R和觀測空間的背景誤差協方差矩陣HPbHT都成為標量。集合均值和集合成員擾動x'i的分析方程為

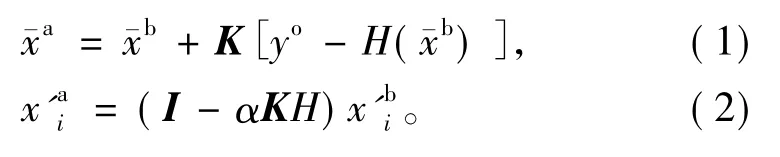
其中:

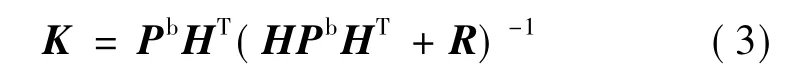
是卡爾曼增益矩陣;Pb是背景誤差協方差矩陣;H是非線性觀測算子H的線性化形式。上標a、b和o分別代表分析場、背景場和觀測場。分析場的集合均值由式(1)更新;而集合成員擾動由方程(2)更新。在單個觀測情況下，

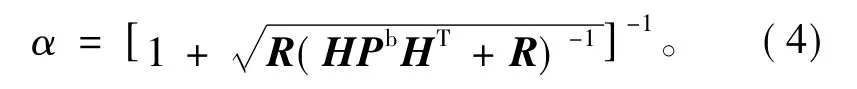
式中平方根根號下分子分母都是標量，所以α值計算簡單。卡爾曼增益矩陣式(3)中的背景誤差協方差矩陣PbHT和HPbHT由預報集合統計來估計，具體形式如下

其中:N是集合成員數。在單一觀測情況下，PbHT是和狀態向量x有相同長度的向量，而HPbHT是標量。在實際應用中，協方差局地化方案通常會用來處理遠距離虛假相關，所以PbHT并不用全部計算，而在觀測影響之外的格點上協方差設為0。當一個觀測同化完后，分析場將作為新的背景場同化下一個觀測。當一個時次所有觀測同化完后，模式將分析場集合作為背景場預報到下一個同化時刻，分析下一個時次的觀測，不斷循環同化過程。

3 試驗設計

3.1 同化方案

本文應用的WRF-EnSRF同化系統是根據En-SRF算法(Whitaker and Hamill，2002)在WRF模式上自主構建的。系統中，狀態向量x中的分析變量包括3個風場分量u、v、w，擾動位勢高度ph，位溫θ，水汽混合比qv，雨水混合比qr，雪水混合比qs以及雹霰混合比qg。為了處理遠距離虛假相關，協方差局地化應用了五階距離相關函數方案(Gaspari and Cohn，1999)，其中水平風場的水平局地化距離為20 km，垂直風場、溫壓場水平局地化距離為15 km，水物質變量的水平局地化距離為10 km，各變量的垂直局地化距離均為10 km。

為了考慮模式誤差的影響，同化方案引入了松弛膨脹方案(Zhang et al.，2004)，以處理分析誤差被低估的問題。松弛膨脹方法是改變分析場的集合離散誤差的一種方法，它通過加權分析擾動場和背景擾動場使分析擾動場發生變化，即:

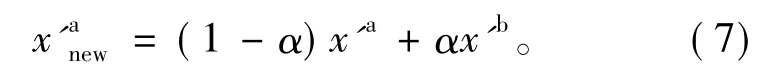
其中:α為背景擾動場的權重，在本文試驗中α值取為0.8;是新的分析擾動場。在試驗中，集合成員數取40，同化的觀測變量yo包括反射率因子Z和徑向速度Vr。該系統處理雷達資料的觀測算子參考Tong and Xue(2005)。徑向速度Vr的計算公式為:

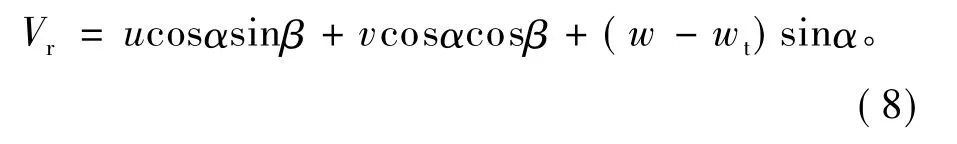
其中:α為雷達掃描的仰角;β為雷達掃描的方位角;wt為雨滴下落末速度;u、v、w為模式模擬的3個速度分量在雷達觀測點上的插值。反射率因子Z的計算公式為:

其中:Ze=Zer+Zes+Zeh。即由雨水混合比qr、雪水混合比qs以及雹霰混合比qg計算，具體公式及參數同Tong and Xue(2005)。反射率因子Z和徑向速度Vr的標準偏差分別取為2 dBz和2 m/s，參考Aksoy et al.(2009)的設置。

3.2 觀測空間診斷

在實際雷達資料的同化試驗中，由于不存在真實場，只能在觀測空間將預報(或分析)的反射率因子和徑向速度與實際觀測的資料進行比較，即通過觀測增量d及相關統計量對試驗結果進行分析(Dowell et al.，2004;Aksoy et al.，2009;Dowell and Wicker，2009)。由于本文主要關注對流系統的預報及分析結果與觀察的偏差，所以只在反射率因子大于10 dBz的對流區域診斷分析及預報結果(Snyder and Zhang，2003;Tong and Xue，2005)。其中:

3個基本的診斷量將被計算:增量均值為〈d〉，〈〉表示在一個雷達體掃的所有觀測上求均值;增量均方差〈r〉，即通過增量與其均值的偏差求取

預報場的集合離散度〈sb〉為

在EnKF方法理論上，預報場的集合離散度可以代表預報誤差的統計特征。在給定的觀測誤差σo和假設背景誤差和觀測誤差不相關并且無偏的情況下，集合離散度和均方差應該是一致的，其比值

應該接近于1(Dowell et al.，2004;Aksoy et al.，2009)。當比值R小于1時，則說明預報場的集合離散度不足。

3.3 試驗設置

在3個強對流天氣個例的控制試驗中，在模式積分開始時(2009年6月14日09:00，2008年6月3日08:00和2005年4月20日08:00)初始場添加隨機擾動形成初始集合。擾動初始場時，速度場(u，v，w)的誤差標準差為3 m/s，位溫θ的誤差標準差為3 K，水汽混合比qv的誤差標準差為1 g/kg。在模式積分到第6 min時系統開始直接同化反射率因子和徑向速度，每6 min同化一次觀測，連續同化至模式的第60 min，并且將第60 min的分析場集合作為初始場，進行30 min集合預報，以進一步考察系統的同化效果(Aksoy et al.，2010)。

為了考察初始擾動時不同強度的位溫和水汽擾動對預報場的集合離散度以及同化效果的影響，在3個強對流天氣過程的雷達資料同化的敏感性試驗中，添加隨機擾動時位溫θ的誤差標準差取為1 K，水汽混合比qv的誤差標準差取為0.5 g/kg，其他設置同控制試驗。

4 結果分析

4.12009 年6月14日颮線

2009年6月14日颮線同化控制試驗在觀測空間的診斷量如圖1所示，經過3個時次的同化(模式的第18 min后)，反射率因子和徑向速度的增量均方差分別維持在10 dBz和4～5 m/s，其增量均值在同化期間迅速減小。從預報時刻負的反射率因子增量均值(圖1a)可以看出，預報場集合平均的反射率因子被高估，在同化后期相對實際觀測偏大2～3 dBz。預報場集合離散度與均方差的比值顯示(圖1 c、d):反射率因子和徑向速度的集合離散度都是不足的，經過60 min的同化，反射率因子的離散度與均方差比值低于0.6，而徑向速度的離散度與均方差比值低于0.4。盡管如此，從試驗結果的增量統計值來看，各觀測變量的分析誤差還是迅速減小并趨于穩定的，沒有發生濾波發散。

經過60 min的同化，分析場集合平均的反射率因子分布如圖2d所示，與相應的實際觀測的反射率因子(圖2a)相比基本一致。

4.22008 年6月3日超級單體風暴

2008年6月3日超級單體風暴觀測空間診斷量如圖3所示。經過42 min同化后，反射率因子和徑向速度的增量均值和均方差趨于穩定。與2009年6月14日颮線相比，反射率因子的增量均方差與其基本相當，而預報時刻的反射率因子增量均值高達－6 dBz，這說明預報的反射率因子被嚴重高估;徑向速度的增量均方差為2.5～4 m/s，與2009年6月14日颮線相比明顯偏小，其增量均值也偏小。同化后期，反射率因子和徑向速度的離散度與均方差比值(圖3 c、d)分別達到0.7左右和0.5左右，明顯高于2009年6月14日颮線的值，這表明該個例的集合離散度相對充足，從而改善了徑向速度的分析。

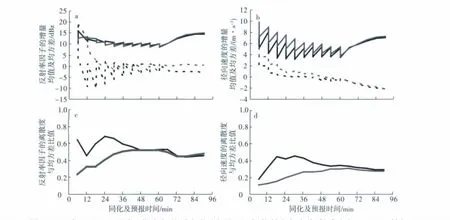
圖1 2009年6月14日颮線同化試驗觀測空間的診斷量(黑線:控制試驗;灰線:敏感試驗)a.反射率因子同化及預報期間的增量均值(虛線)和增量均方差(實線);b.徑向速度同化及預報期間的增量均值(虛線)和增量均方差(實線);c.反射率因子預報場集合離散度與均方差的比值;d.徑向速度預報場集合離散度與均方差的比值Fig.1 Assimilated observation-space diagnosis of convective line on 14 June 2009(black line:control experiment;grey line:sensitivity experiment)a.the forecast and analysis(sawtooth pattern)root mean square innovation(solid line)and mean innovation(dashed line)of the effective reflectivity factor;b.the forecast and analysis(sawtooth pattern)root mean square innovation(solid line)and mean innovation(dashed line)of the radial velocity;c.the forecast actual/optimal spread ratio of the effective reflectivity factor;d.the forecast actual/optimal spread ratio of the radial velocity

第60 min分析時刻的反射率因子分布如圖2e所示，強回波帶(33°N附近主要的兩個對流區，其中回波較強區域較大的系統即為超級單體風暴)可以較準確的分析出來，而反射率因子大于40 dBz區域相對觀測(圖2b)明顯偏大，這與觀測空間診斷結果中反射率因子被嚴重高估一致。

4.32005 年4月20日多單體風暴

2005年4月20日多單體風暴的觀測空間診斷量如圖4所示，反射率因子的增量均值與均方差結果與2009年6月14日颮線的基本一致;而徑向速度的增量均值和均方差在3個個例中最大。另外徑向速度的離散度與均方差比值在3個個例中也最小，小于0.25。這說明當集合離散度過分不足，背景誤差協方差不能準確估計時，同化效果即偏差。

最后分析時刻的反射率因子分布如圖2f所示，若干個強回波區(反射率因子大于35 dBz)與觀測(圖2c)基本一致。

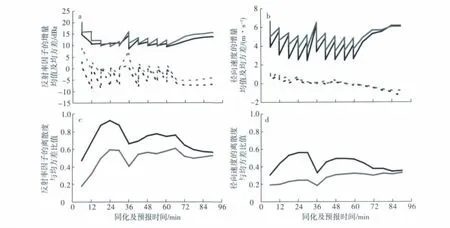
圖3 2008年6月3日超級單體風暴觀測空間診斷量(黑線:控制試驗;灰線:敏感試驗)a.反射率因子同化及預報期間的增量均值(虛線)和增量均方差(實線);b.徑向速度同化及預報期間的增量均值(虛線)和增量均方差(實線);c.反射率因子預報場集合離散度與均方差的比值;d.徑向速度預報場集合離散度與均方差的比值Fig.3 Assimilated observation-space diagnosis of supercell on 3 June 2008(black line:control experiment;grey line:sensitivity experiment)a.the forecast and analysis(sawtooth pattern)root mean square innovation(solid line)and mean innovation(dashed line)of the effective reflectivity factor;b.the forecast and analysis(sawtooth pattern)root mean square innovation(solid line)and mean innovation(dashed line)of the radial velocity;c.the forecast actual/optimal spread ratio of the effective reflectivity factor;d.the forecast actual/optimal spread ratio of the radial velocity

4.4 模式空間

由于沒有直接的高分辨率觀測與模式空間的要素場進行比較，這里只能利用強對流系統的概念模型對3個系統的分析場進行定性分析。基于這一目的，模式第60 min的集合平均分析場在模式最底層(100 m高度)的水平風場和擾動位溫場以及模式第8層(1 600 m高度)的垂直風場如圖5所示。3個個例中，各系統相應的區域均有冷池并且伴有明顯的輻散氣流。

2009年6月14日颮線中，輻散氣流最強的區域(系統的南部)與兩個強上升運動區(垂直速度大于2 m/s)連成明顯的線型區域基本重合，并且與線型的強回波帶非常一致(圖2a)。2008年6月3日超級單體風暴的系統區域對應著上升運動，同時從擾動位溫場可以看出該次強對流過程是冷鋒南下觸發而形成。在同化效果較差的2005年4月20日多單體風暴中，系統區域有不規則的上升運動，但是在系統的南邊有更明顯的冷池對應著更強的上升運動，這可能由于同化過程中產生的虛假單體發生發展而形成的不合理的動力結構，另外該虛假單體區域沒有雷達觀測資料，所以雷達資料同化對這一區域的虛假單體的發生發展基本不起作用。

4.5 集合預報

為了考察分析場的質量，本文在試驗中以經過60 min同化的分析場集合為初始場進行30 min集合預報。從3個個例在觀測空間的診斷結果來看(圖1、圖3和圖4)，預報誤差都隨時間迅速增長。在模式的第90 min，反射率因子增量均方差都達到15 dBz左右，其中超級單體風暴的集合預報效果最好，徑向速度的增量均方差為6 m/s;而多單體風暴的徑向速度增量均方差增長最快數值最大，所以其同化效果最差。

4.6 不同擾動強度熱力場的影響

通過對比控制試驗與敏感試驗結果(圖1、圖3和圖4)，本文分析了初始場添加擾動時位溫和水汽的不同擾動強度對同化試驗和集合預報的影響。在敏感試驗中，由于位溫和水汽的擾動強度偏小，各個個例的反射率因子和徑向速度在同化階段的集合離散度更加不足，這說明熱力場的擾動強度變化對動力場的集合離散度有較大影響。通過觀測空間的診斷結果可以看出，在敏感試驗的同化階段徑向速度的增量均值和均方差收斂較慢，其誤差偏大，但在集合預報階段其誤差大小與控制試驗趨于一致;敏感試驗中反射率因子的增量均值相對偏小，而其增量均方差與控制試驗基本相當。值得注意的是控制試驗中反射率因子增量均值在預報時刻一直是負值，這表明熱力場擾動強度增加時預報的反射率因子偏強，這可能由于對流系統發展偏強和虛假回波增多引起的。

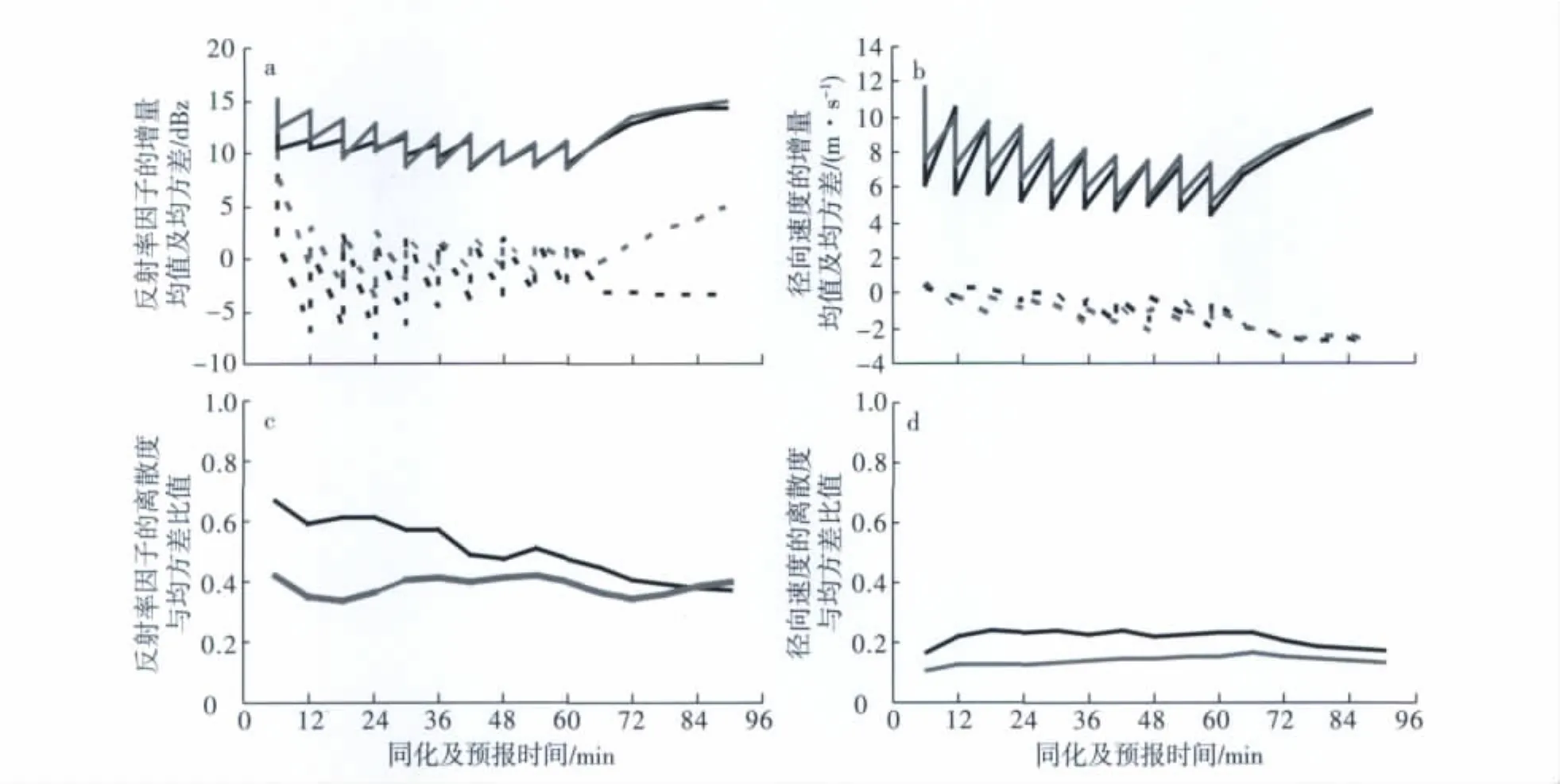
圖4 2005年4月20日多單體風暴觀測空間診斷量(黑線:控制試驗;灰線:敏感試驗)a.反射率因子同化及預報期間的增量均值(虛線)和增量均方差(實線);b.徑向速度同化及預報期間的增量均值(虛線)和增量均方差(實線);c.反射率因子預報場集合離散度與均方差的比值;d.徑向速度預報場集合離散度與均方差的比值Fig.4 Assimilated observation-space diagnosis of multicell on 20 April 2005(black line:control experiment;grey line:sensitivity experiment)a.the forecast and analysis(sawtooth pattern)root mean square innovation(solid line)and mean innovation(dashed line)of the effective reflectivity factor;b.the forecast and analysis(sawtooth pattern)root mean square innovation(solid line)and mean innovation(dashed line)of the radial velocity;c.the forecast actual/optimal spread ratio of the effective reflectivity factor;d.the forecast actual/optimal spread ratio of the radial velocity

5 結論與討論

本文基于風暴尺度模式，利用EnSRF同化實際多普勒雷達資料，在3個獨立的不同類型的強對流天氣過程(颮線、超級單體風暴和多單體風暴)進行同化試驗。徑向速度和反射率因子在分析時刻的增量均方差在經過24 min同化后分別下降至3～5 m/s和10 dBz，并維持至60 min同化結束。反射率因子的誤差較大可能是由于微物理過程參數化方案和觀測算子的不完善引起的。從試驗結果可以看出，反射率因子和徑向速度的預報集合離散度都被低估。盡管如此，各試驗均未發生濾波發散現象。集合離散度不足是EnKF研究的普遍問題，這主要是模式誤差，環境場的不確定性和集合樣本誤差等問題引起的。在各控制試驗中，分析場集合平均的反射率因子分布與實際觀測比較一致，這表明En-SRF系統能夠較好的重構各類型強對流天氣系統的形狀特點。在模式空間，分析場中近地面層有冷池和明顯的輻散氣流并伴有空中的上升運動，各要素的結構配置基本合理，符合各類型強對流系統的動力結構特征。

集合預報結果中，隨時間演變預報質量迅速下降，徑向速度增量均方差不同反映了不同個例的可預報性不同。同時可以看出，同化系統得到的分析場集合為集合預報提供初值，使兩者有效結合的方式是有應用潛力的。

預報場的集合離散度對熱力場的擾動強度比較敏感。初始場添加擾動時，適當增加位溫和水汽的擾動強度有利于提高預報場的集合離散度，使得徑向速度誤差在同化階段收斂更快，誤差更小，但是這樣也會使得反射率因子系統性誤差偏大。所以熱力場擾動強度的合理選取對于EnSRF同化試驗是比較重要的，需通過多組試驗取得。

總的來說，對于3個不同類型的強對流天氣過程WRF-EnSRF同化系統均表現出有效的同化性能，展現了EnSRF同化在風暴尺度的應用潛力。但是，預報集合離散度被低估的問題依然存在，在以后的研究中我們需要加強對模式誤差，環境場的不確定性和集合樣本誤差等問題的研究，以更好的解決集合離散度不足的問題，充分發揮WRF-EnSRF同化系統的潛力。

陳力強，楊森，肖慶農.2009.多普勒雷達資料在冷渦強對流天氣中的同化應用試驗［J］.氣象，35(12):12-21.

蘭偉仁，朱江，Xue Ming，等.2010a.風暴尺度天氣下利用集合卡爾曼濾波模擬多普勒雷達資料同化試驗I.不考慮模式誤差的情形［J］.大氣科學，34(3):640-652.

蘭偉仁，朱江，Ming Xue，等.2010b.風暴尺度天氣下利用集合卡爾曼濾波模擬多普勒雷達資料同化試驗II.考慮模式誤差的情形［J］.大氣科學，34(4):737-753.

閔錦忠，彭霞云，賴安偉，等.2007.反演同化和直接同化多普勒雷達徑向速度的對比試驗［J］.南京氣象學院學報，30(6):745-754.

潘敖大，王桂臣，張紅華，等.2009.多普勒雷達資料對暴雨定量預報的同化對比試驗［J］.氣象科學，29(6):755-760.

謝義明，解令運，沙維茹，等.2008.江蘇中部一次強對流天氣的物理機制分析［J］.氣象科學，28(2):212-216.

許小永，劉黎平，鄭國光.2006.集合卡爾曼濾波同化多普勒雷達資料的數值試驗［J］.大氣科學，30(4):712-728.

周昆，陳斌，盧逢剛.2008.安徽省2008年初夏1次強對流天氣的分析［J］.安徽農業科學，36(25):11060-11062.

Aksoy A，Dowell D C，Snyder C.2009.A multi-case comparative assessment of the ensemble Kalman filter for assimilation of radar observations.PartⅠ:Storm-scale analyses［J］.Mon Wea Rev，137:1805-1824.

Aksoy A，Dowell D C，Snyder C.2010.A multi-case comparative assessment of the ensemble Kalman filter for assimilation of radar observations.PartⅡ:Short-range ensamble forecasts［J］.Mon Wea Rev，138:1273-1292.

Anderson J L，Collins N.2007.Scalable implementations of ensemble filter algorithms for data assimilation［J］.J Atmos Oceanic Technol，24:1452-1463.

Dowell D C，Wicker L J.2009.Additive noise for storm-scale ensemble data assimilation［J］.J Atmos Oceanic Technol，26:911-927.

Dowell D C，Zhang F，Wicker L，et al.2004.Wind and temperature retrievals in the 17 May 1981 Arcadia，Oklahoma，supercell:Ensemble Kalman filter experiments［J］.Mon Wea Rev，132:1982-2005.

Evensen G.1994.Sequential data assimilation with a non-linear quasigeostrophic model using Monte Carlo methods to forecast error statistics［J］.J Geophys Res，99(C5):10143-10162.

Gaspari G，Cohn S E.1999.Construction of correlation functions in two and three dimensions［J］.Quart J Roy Meteor Soc，125:723-757.

Houtekamer P L，Mitchell H L.1998.Data assimilation using an ensemble Kalman filter technique［J］.Mon Wea Rev，126:796-811.

Snyde C，Zhang F.2003.Assimilation of simulated Doppler radar observations with an ensemble Kalman filter［J］.Mon Wea Rev，131:1663-1677.

Sun J，Crook N A.1997.Dynamical and microphysical retrieval from Doppler radar observations using a cloud model and its adjoint.PartⅠ:Model development and simulated data experiments［J］.J Atmos Sci，54:1642-1661.

Sun J，Crook N A.1998.Dynamical and microphysical retrieval from Doppler radar observations using a cloud model and its adjoint.PartⅡ:Retrieval experiments of an observed Florida convective storm［J］.J Atmos Sci，55:835-852.

Tong M.2006.Ensemble Kalman filter assimilation of Doppler radar data for the initialization and prediction of convective storms［D］.O-klahoma University of Oklahoma:243.

Tong M，Xue M.2005.Ensemble Kalman filter assimilation of Doppler radar data with a compressible nonhydrostatic model:OSS experiments［J］.Mon Wea Rev，133:1789-1807.

Whitaker J S，Hamill T M.2002.Ensemble data assimilation without perturbed observations［J］.Mon Wea Rev，130:1913-1924.

Xue M，Tong M，Droegemeier K K.2006.An OSSE framework based on the ensemble square-root Kalman filter for evaluating impact of data from radar networks on thunderstorm analysis and forecast［J］.J Atmos Oceanic Technol，23:46-66.

Zhang F，Snyder C，Sun J.2004.Impacts of initial estimate and observation availability on convective-scale data assimilation with an ensemble Kalman filter［J］.Mon Wea Rev，132:1238-1253.

A numerical experiment on WRF-EnSRF for assimilation of Doppler Radar data in multicase strong convective weather processes

CHEN Jie1，2，MIN Jin-zhong2，WANG Shi-zhang2，WANG Xiao-ci2

(1.Unit 94701，PLA，Anqing 246001，China;2.Key Laboratory of Meteorological Disaster of Ministry of Education，NUIST，Nanjing 210044，China)

The effectiveness of the EnSRF(ensemble square root filter)data assimilation system in assimilating Doppler radar data on convective scales is investigated for cases whose behaviors span supercellular，linear，and multicellular organizations.The impacts of potential temperature and water vapor at different levels on ensemble spread and assimilation effect during initial perturbations are also investigated.The EnSRF performs effectively and produces results of comparable quality for each of the cases.The root mean square innovations of radial velocity and reflectivity decrease to 3—5 m/s and about 10 dBz respectively after roughly 24 min of assimilation and maintain the values throughout to the end of the 60 min period of assimilation.The ensemble spread and assimilation effect are sensitive to the magnitude of perturbation in thermal field，which implies that larger ensemble spread and better radial velocity analysis can be obtained by increasing the standard deviation of potential temperature and water vapor mix ratio appropriately during initial perturbation.

EnSRF;storm scale;Doppler radar data

P459.9

A

1674-7097(2012)06-0720-10

2011-01-17;改回日期:2011-05-21

公益性行業(氣象)科研專項(GYHY(QX)200806029);科技創新工程重大項目培育基金項目(708051);國家自然科學基金資助項目(40975068)

陳杰(1985—)，男，安徽明光人，碩士，研究方向為雷達資料同化，chenjie20021301189@sina.com.

陳杰，閔錦忠，王世璋，等.2012.WRF-EnSRF系統同化多普勒雷達資料在多類型強對流天氣過程的數值試驗［J］.大氣科學學報，35(6):720-729.

Chen Jie，Min Jin-zhong，Wang Shi-zhang，et al.2012.A numerical experiment on WRF-EnSRF for assimilation of Doppler Radar data in multicase strong convective weather processes［J］.Trans Atmos Sci，35(6):720-729.(in Chinese)

(責任編輯:張福穎)