模糊神經網絡在冷連軋厚度控制中的應用

薛 薇，吳青華

(天津科技大學電子信息與自動化學院，天津 300222)

模糊神經網絡在冷連軋厚度控制中的應用

薛 薇，吳青華

(天津科技大學電子信息與自動化學院，天津 300222)

由于冷連軋厚度控制系統具有非線性、大時滯的特點，在冷連軋厚度的常規 PID控制中，PID控制器的參數往往針對某一種情況進行整定，很難控制冷連軋厚度始終處于一個好的狀態.為此，在分析了厚度控制原理的基礎上，設計了用一個2-5-1結構的BP網絡實現的模糊神經網絡控制器(FNNC)，并將該FNNC控制器與積分作用相結合構成一個FNNC-I控制器.仿真結果表明，該FNNC-I控制器提高了系統的動態和穩態性能、抗干擾性以及魯棒性，其控制效果優于常規PID控制器.

冷連軋；厚度控制；模糊神經網絡；PID

在冷軋過程中，自動厚度控制(AGC)是冷連軋機控制系統的重要組成部分，其性能的優劣直接影響產品的質量，同時還會影響板型控制的精度.因此，自動厚度控制對提高產品的厚度和板形精度有重要的意義.

早期采用的是直接測量厚度的反饋式自動厚度控制[1]，通常采用常規PID控制.常規PID控制器原理簡單、設計方便，在工業控制中被廣泛應用，但控制器對系統模型的精確性依賴較強，對于非線性、時變且受隨機干擾的系統，一般難以獲得較好的控制性能[2].雖然冷連軋厚度的測量儀器(比如 KELK 公司生產的張力測量儀)測出的精度較高，經二次儀表處理后實時性也較好，但是測量點與執行器的工作點存在著較大距離，因此系統存在較大的滯后；而且在執行器執行時，又存在液壓系統的響應滯后.按照常規PID控制方式，控制系統響應不及時，必然導致系統超調量大，調節時間長，控制效果不佳；在實際應用中很難獲得高精度的厚度控制數學模型，這也使得依賴高精度數學模型的 PID控制在厚度控制上不能發揮其優勢.換言之，冷連軋機是復雜的機、電、液多變量耦合的大滯后的物理系統，在實際軋制過程中影響機架厚度的工藝參數很多，厚度的變化又對其他工藝參數產生相互影響.若采用PID控制，很難達到厚度控制系統的要求，因此越來越多的研究人員開始關注智能方法在厚度控制中的應用[3].一種做法是采用Smith預估器進行補償[4–5]，但Smith預估器的抗干擾能力較差，且對數學模型的誤差十分敏感，模型失匹會使得系統穩定性和魯棒性變差.而模糊神經網絡控制器由于具有良好抗干擾性和魯棒性，在許多工業過程中得到了廣泛的應用[6–8].

本文設計一個 3層結構的 BP網絡實現的模糊神經網絡控制器(FNNC)，該模糊神經網絡控制器結構及算法簡單、實現方便.為了提高控制系統的穩態性能，在此基礎上將 FNNC控制器與積分作用相結合，構成了一個 FNNC-I控制器.該控制器在厚度控制中取得了較好的控制效果.

1 厚度控制系統模型

以酸洗五連軋聯合機組的軋機為例，對輥縫內環進行 PID控制，并考慮測厚儀滯后的影響，可以得到整個厚度環被控對象的傳遞函數[1]為

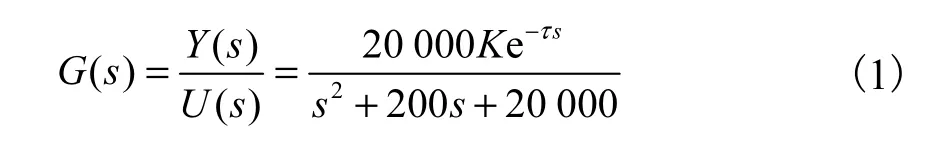
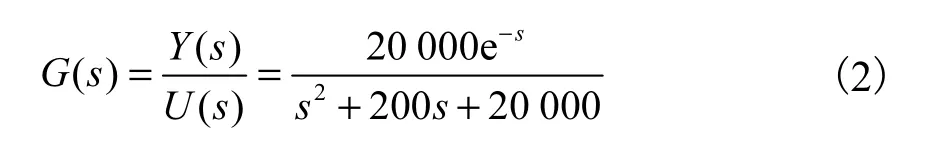
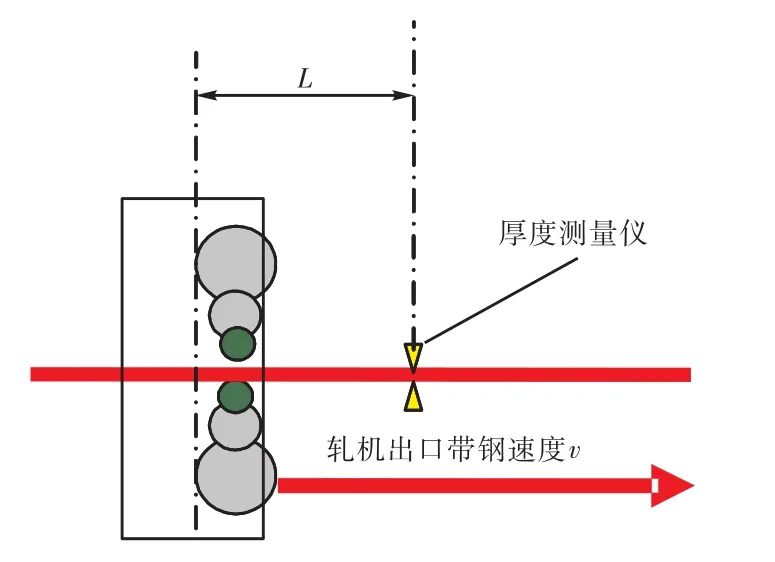
圖1 軋機示意圖Fig.1 Schematic diagram of mill

2 模糊神經網絡控制系統

2.1 FNNC結構與算法

2.1.1 FNNC的結構

本文采用的模糊神經網絡控制器結構框圖如圖2所示.

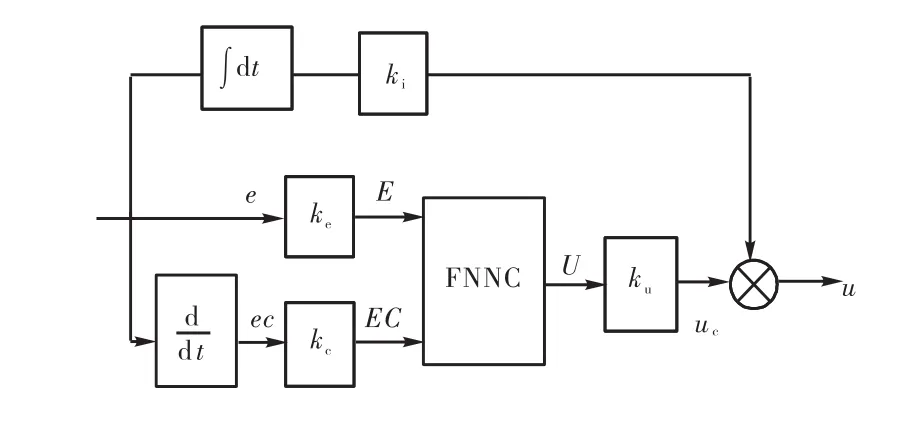
圖2 FNNC的原理結構圖Fig.2 Structrue diagram of FNNC principle

為了更好地提高系統的穩態性能，在 FNNC基礎上再并聯一個積分控制環節，構成一個 FNNC-I控制器.圖中，ke為誤差量化因子，kc為誤差變化量化因子，ku為控制器輸出的比例因子，ki為積分環節放大系數.

模糊系統善于直接表示邏輯，適于直接表示知識；神經網絡長于學習，通過數據隱含表達知識.對于模糊神經網絡控制器，如何把模糊邏輯推理與神經網絡技術相結合，采用什么樣的神經網絡結構來實現模糊邏輯控制作用，大多數學者提出的網絡結構都是與模糊邏輯推理的前后件相匹配的結構，這樣的網絡結構較為復雜，一般為 4層或 5層網絡，其算法復雜、訓練及學習過程較長，不便于進行實時控制和應用開發[10].

本文采用的模糊邏輯和神經網絡相結合的方式是用神經網絡學習并記憶模糊規則的控制.即通過一組神經元不同程度的興奮表達一個抽象的概念值，由此將抽象的經驗規則轉化成神經網絡的輸入輸出樣本，通過神經網絡學習并記憶這些樣本，控制器以聯想記憶方式使用這些經驗，在一定意義上與人的聯想記憶思維方式接近.神經網絡中應用最廣的是多層前向網絡，多層前向網絡應用于具體實時控制問題時，必須有一個訓練網絡權值的算法，應用最廣的是BP算法，這種算法思路簡潔明了，具有自適應、自學習、自組織功能.考慮到 BP網絡已經成功地應用于多種控制系統，并且其結構簡單、易于實現，選用 3層的BP網絡作為模糊神經網絡控制器[11]，其結構如圖3所示.

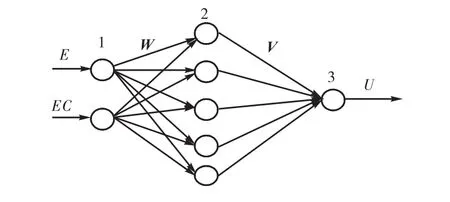
圖3 BP網絡結構圖Fig.3 Structrue diagram of BP network

圖3是一個2-5-1結構的BP網絡，輸入層節點有 2個，分別是誤差E和誤差變化EC；中間層節點有 5個，這一層的節點數目不是固定不變的，可以根據實際情況進行調整，一般為 5個左右；輸出層節點只有一個，即控制量U.

2.1.2 FNNC算法

BP 網絡采用如下控制算法[11–12]：

式中：t為訓練次數；n0(t)為輸入樣本函數；n(t)為網絡實際輸出函數.學習算法采用帶有阻尼項的BP算法，即

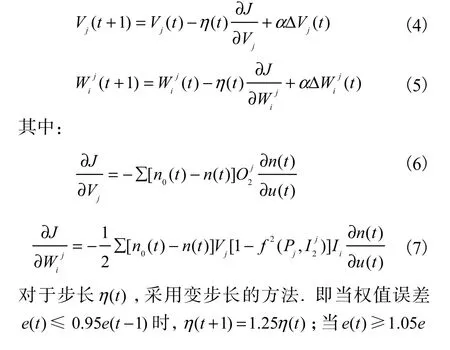
2.2 初始權值的確定

厚度控制中的神經網絡初始值可以由模糊控制表作為學習樣本離線學習得到.這里選用帶有自調整因子的模糊控制器的輸入、輸出構成模糊控制表.即

經過樣本學習后得到的初始權值組成的模糊神經網絡控制器，在控制初期就已經被賦予了人的操作經驗.

3 仿真研究

3.1 PID穩定域的確定與參數整定

為了更好地對 PID控制器進行參數整定，首先使用確定 PID參數穩定域的圖解法[13]，在參數空間中，用擬多項式(Quasi-Polynomial)穩定的一個圖解準則，直接繪出PID參數的穩定域.然后在所確定的穩定域中選擇一組合適的PID參數.

按照文獻[13]給出的圖解法，在確定kp＝0.025時，繪制出kd，ki的穩定域如圖 4所示.圖 4中的陰影區為kd、ki參數穩定區.在穩定域范圍內，kp＝0.025，kd＝0.01，ki＝0.45時系統響應曲線最佳，因此，選取這組參數作為PID控制器參數.

圖4 kp=0.025時，kd和ki的穩定域Fig.4 Stabilizing regions ofkdandkiwhenkp=0.025

3.2 模糊神經網絡與傳統PID的仿真結果

PID控制器的參數整定為：kp＝0.025，kd＝0.01，ki＝0.45；FNNC-I控制器的參數按經驗整定為：ke＝5，kc＝0.01，ku＝1，ki＝0.42.

不加任何干擾，在單位階躍信號的作用下，兩種控制器的仿真結果見圖 5.在單位階躍信號的作用下，t=15s時，加相同幅值為 0.25的階躍擾動，兩種控制器的仿真結果見圖6.

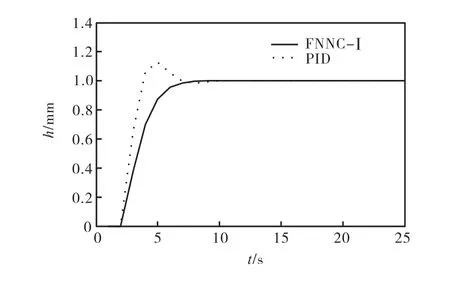
圖5 無干擾時的仿真結果對比Fig.5 Comparison of simulation when noninterference

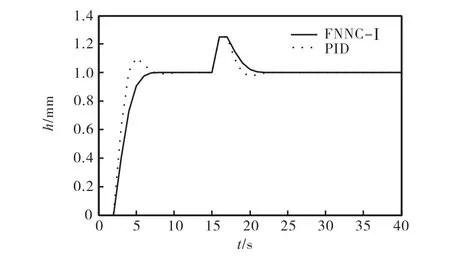
圖6 加干擾時的仿真結果對比Fig.6 Comparison of simulation when interference

由圖5可以看出，FNNC-I沒有超調，而 PID控制器的超調明顯，達到12%.圖6中，在有干擾的情況下，PID 的抗干擾能力不如 FNNC-I，PID 控制存在負超調.

由于冷軋機組軋制速度是可變的，這樣就造成系統控制對象的滯后時間不一樣.當滯后時間τ=2s時，PID控制器和 FNNC-I控制器的響應曲線見圖7.滯后時間τ=3s時，PID控制器和FNNC-I控制器的響應曲線見圖8.

在圖7中的仿真結果中，PID控制器最大超調為38%，而此時 FNNC-I沒有超調.在圖 8中的仿真結果中，PID控制器最大超調為63%，FNNC的超調只有1%.隨著延時時間的加長，PID控制器的超調明顯變大，調節時間變長.由此可以看出，在系統模型參數改變時，FNNC-I控制系統比傳統的PID控制系統具有更好的動態、穩態性能，響應速度快且超調小.這說明模糊神經網絡控制對被控對象精確數目模型的依賴性明顯小于傳統的PID控制.

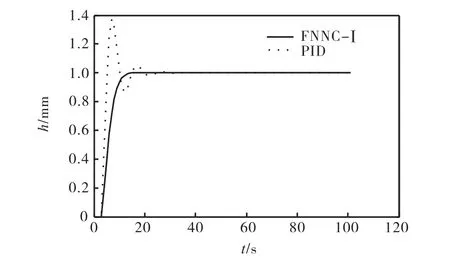
圖7 延時時間τ=2s時的仿真結果對比Fig.7 Comparison of simulation whenτ=2s

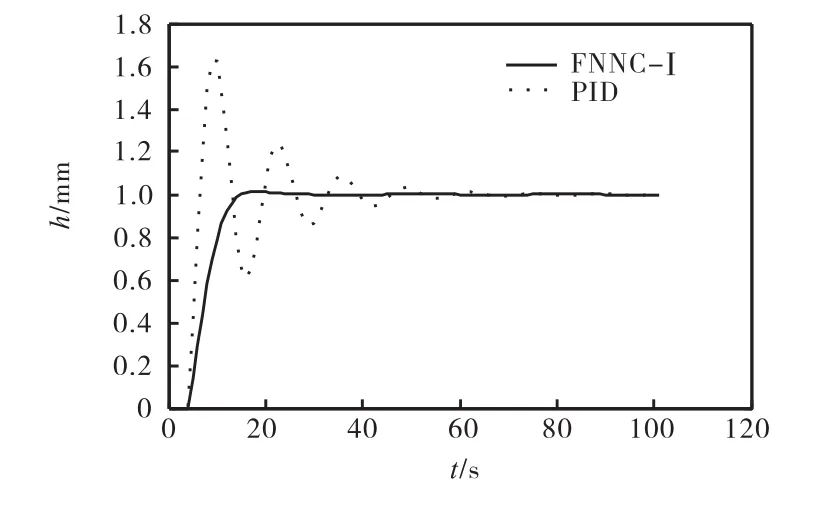
圖8 延時時間τ=3s時的仿真結果對比Fig.8 Comparison of simulation when τ=3s

4 結 語

本文針對冷連軋AGC系統對象存在較大的時滯以及過程模型參數變化的特點，提出一種帶積分環節的模糊神經網絡控制器(FNNC-I)的解決方案.仿真驗證說明，該模糊神經網絡控制策略用于軋機的厚度控制是可行的，能穩定控制軋制厚度，并有較好的控制效果.

［1］孫一康. 帶鋼冷連軋計算機控制[M]. 北京：冶金工業出版社，2002.

［2］趙慶海，賈中華. 模糊自適應 PID 控制在張力控制中的應用[J]. 包裝工程，2008，29(1)：87–89.

［3］賈春玉. 基于模糊神經網絡推理的智能厚度控制[J].鋼鐵研究學報，2001，13(2)：50–53.

［4］李伯群. 熱連軋厚度綜合控制技術的應用研究[D]. 北京：北京科技大學，2006.

［5］陳連貴，楊衛東，楊斌虎. 基于魯棒二自由度增益自適應 Smith預估器的冷軋厚度計型 AGC[J]. 北京科技大學學報，2007，29(6)：632–635.

［6］牛培峰，高龍，陳貴林，等. 模糊神經網絡自適應控制在循環流化床鍋爐燃燒控制系統中的應用研究[J]. 燕山大學學報，2011，35(4)：328–333，350.

［7］周水英，蔡杰，鐘漢如. 基于模糊神經網絡的氣流霧化染色機溫度控制[J]. 制造業自動化，2011，33(17)：116–119.

［8］葛超，孫艷彬，張景春，等. 基于模糊神經網絡的鍋爐蒸汽壓力控制系統[J]. 可編程控制器與工廠自動化，2010(1)：87–89.

［9］李仲德，楊衛東. 冷連軋 AGC系統的自適應Smith廣義預測控制[J]. 信息與控制，2009，38(5)：575–579.

［10］趙振宇，徐用懋. 模糊理論和神經網絡的基礎與應用[M]. 北京：清華大學出版社，1996.

［11］薛薇，齊國元，李力，等. pH過程的FNNC–PI控制研究[J]. 儀器儀表學報，2004，25(6)：721–724，733.

［12］Xue Wei，Guo Yanling. Fuzzy neural network control in main steam temperature system[J]. ICIC Express Letters，2009，3(3)：409–414.

［13］王德進. 一種確定 PID參數穩定域的圖解法[J]. 控制與決策，2007，22(6)：663–666.

Fuzzy Neural Network on the Application in Thickness Control of Tandem Cold Mill

XUE Wei，WU Qinghua
(College of Electronic Information and Automation，Tianjin University of Science & Technology，Tianjin 300222，China)

There are nonlinear，large time delay characteristics of tandem cold mill thickness control，so it is difficult to keep thickness within a small tolerance using PID controller，whose parameters are set only for one stable situation. Based on the analysis of thickness control theory，a fuzzy neural network controller(FNNC)with simple structure was designed，which was realized by a BP network with 2-5-1 structure. On the basis of this controller，anintergral action was added to constitute FNNC-I controller. Simulation results show that the dynamic，static，anti-interference performance and the robusness of the system were all improved by this FNNC-I controller，so it is better than the conventional PID controller.

tandem cold mill；thickness control；fuzzy neural network；PID

TG335.5

A

1672-6510(2012)02-0049-04

2011–11–14；

2012–01–06

國家自然科學基金資助項目(60874028)

薛 薇（1963—），女，河北河間人，副教授，xuewei@tust.edu.cn.

常濤