Oscillation for the Solutions of Hyperbolic Partial Differential Equation with Damped Terms and High order Laplace Operator

GAO Zheng－hui ，LUO Li－ping，YANG Liu

（Department of Mathematics and Computational Science，Hengyang Normal University，Hengyang Hunan 421002，China）

0 Introduction

The theory of the nonlinear differential equations with delay can be applied to many fields，such as biological medicine，engineering technology，physics and so on.Oscillation theory for the solution of the functional differential equation with delay is an important part to study functional differential equations.Oscillations of the solution for the delay hyperbolic partial differential equation has been studied by a number of authors，plenty of research achievements have been published，see［1－5］.However，a few of papers have been published on oscillation of the solution for the delay hyperbolic partial differential equation containing damped terms，see［6－7］.the relative research results of the oscillation of the solution for the continuous delay argument partial functional differential equation with damped terms are few，see［8］.In this paper，we studied the oscillatory behaviors of the continuous delay argument hyperbolic partial differential equation with damped terms and high order Laplace operator

with following boundary value conditions

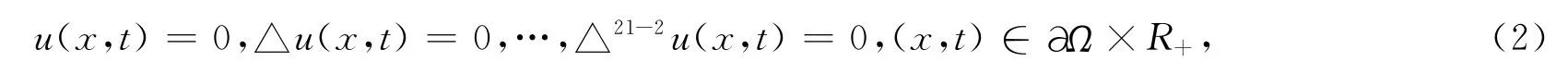
where（x，t）∈Ω×R＋≡G，R＋＝［0，∞］，Ω?Rnis bounded，?Ωis piecewise smooth，l≥1is integral，△is Laplace operator，and△nu＝△（△n－1u），n≥1and nare integers，when n＝0，△nu＝u.

For the equation（1），suppose that the following conditions hold：

（C2）Bi（x，t，τ）∈C（×［a，b］；R＋），Bi（t，τ）＝min｛Bi（x，t，τ），x∈｝.

（C3）αi（t，τ），βj（t，τ）∈C（R＋×［a，b］；R＋），αi（t，τ）≤t，βj（t，τ）≤t，αi（t，τ），βj（t，τ）t，τare nondecreasing functions，α（t，τ）＝，and＋∞.（C4）m（τ）is nondecreasing real function onτin［a，b］，the integration in（1）is Stieltjes integration.（C5）fi（u）∈C（R；R），and，if u≠0，it exists constants Mi＞0，such that（C6）p（t）∈C（R＋；R＋），C（t）∈C（R＋；R＋），Dj（t，τ）∈C（R＋×［a，b］；R＋）.

Definition 1A function u（x，t）∈C2（G）∩C1（G－）is called a solution of the problem（1），（2），if it satisfies（1）in the domain G along with the boundary value condition.

Definition 2A solution u（x，t）of equation（1）is called oscillatory in the domain G，if for each positive

numberμhere exists a point（x0，t0）∈Ω×［μ，＋∞］，such that the condition u（x0，t0）＝0holds，Otherwise，u（x，t）is called nonoscillatory.

The purpose of this paper are obtained some new sufficient conditions for the oscillation of each solution of the equation by using integral averaging technique and Riccati transformation.1 The main results

Lemma 1［9］The problem of eigenvalue（λis a constant）

The minimal eigenvalueλ0＞0，and its corresponding eigenfunctionφ0（x）＞0，x∈Ω.

Theorem 1For the equation（1），（2），if condition（C1）—（C6）holds，there exists functionφ（t）∈（t）∈C1（R＋，R＋）satisfy

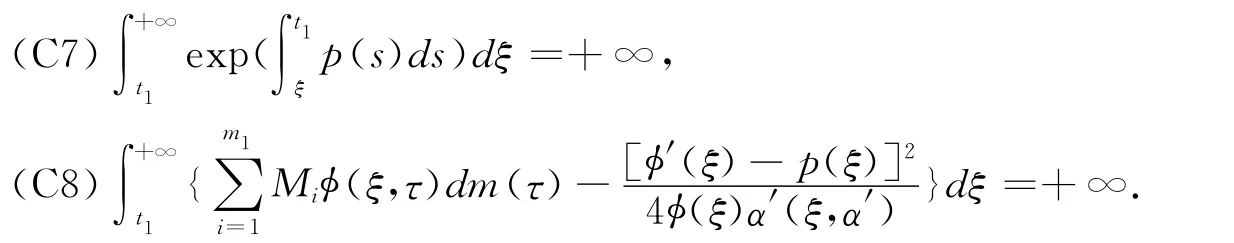
then every solution of the equation（1），（2）is oscillated in G.

proof：Suppose u（x，t）are the nonoscillatory solutions of the equation（1）（2），that there existsμ＞0，when t＞μ，without loss of generality，we may assume that u（x，t）＞0，（x，t）∈Ω×［μ，＋∞］.

For the equation（1），both sides multiplied byφ0（x）＞0，and integrating with respect to xoverΩ，we can get

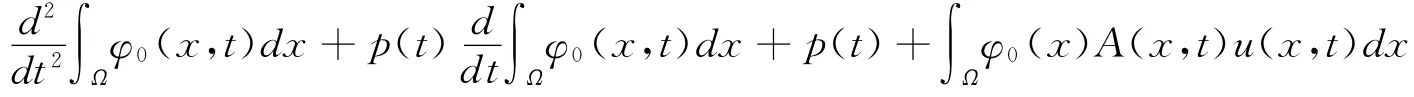
By Green's formula and boundary value condition（2），we have

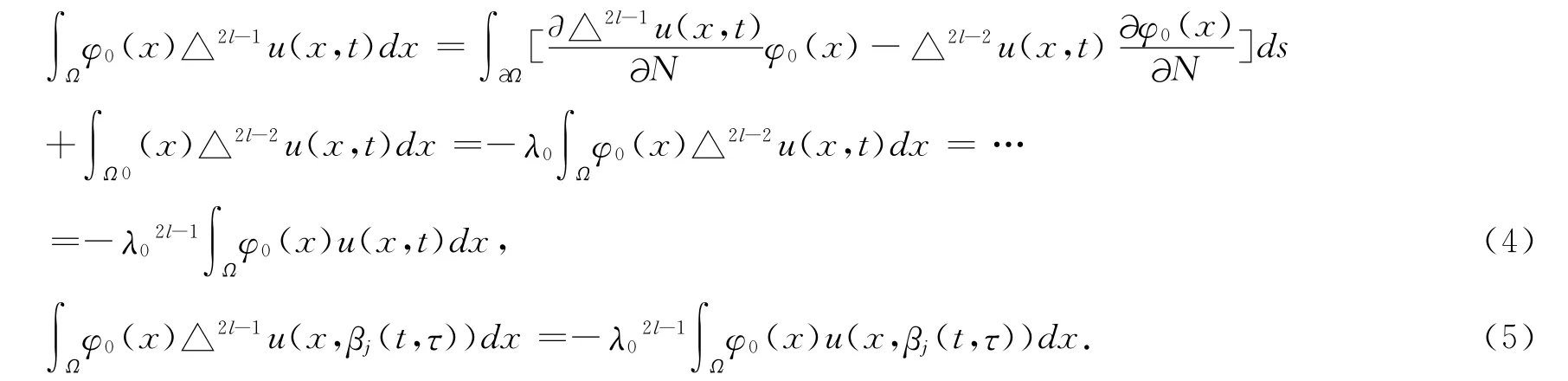
From conditions（C1）—（C6）：

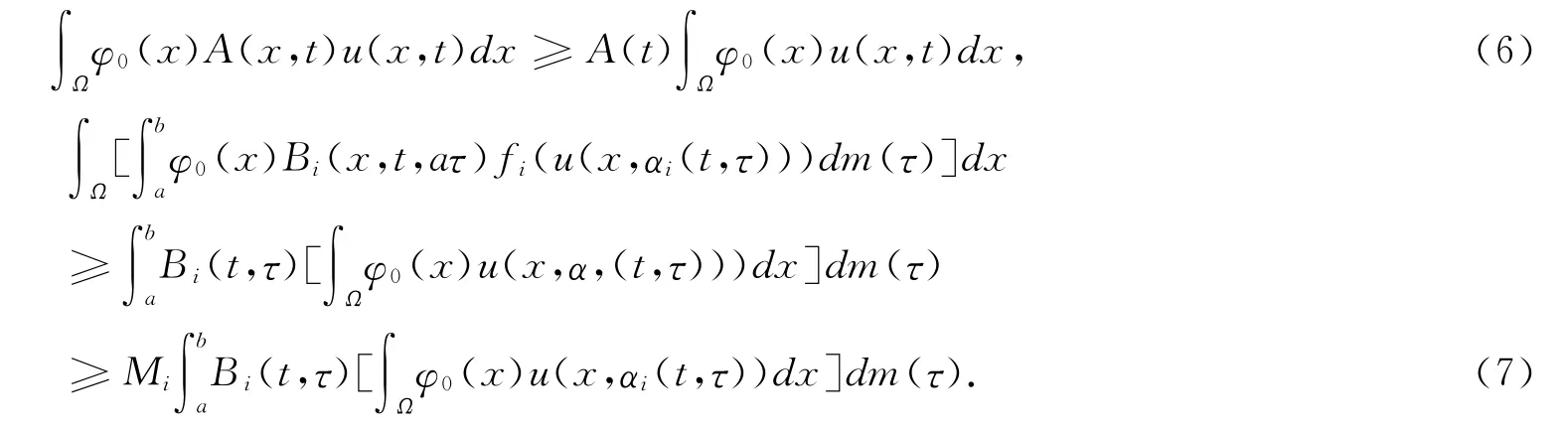
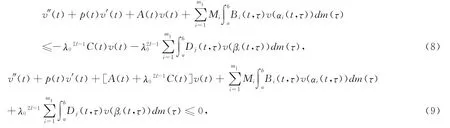
then

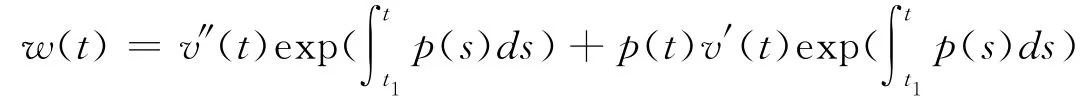
multiplied both sides of（10）by

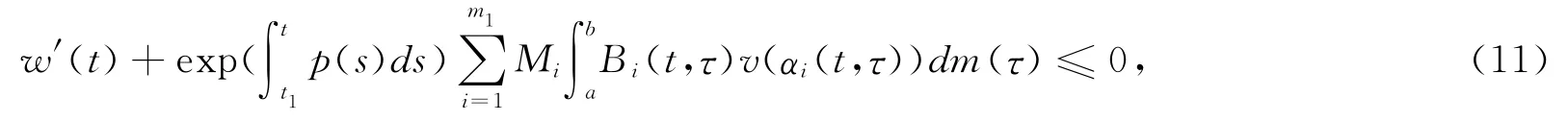
so w′（t）≤0，and w（t）≤w（t1）.

To prove when t≥t1＞0，w（t）≥0.or，if w（t）＜0，w（t）≤w（t1）＝α＜0.

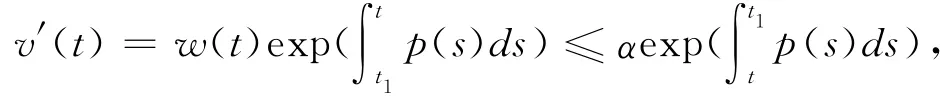
then

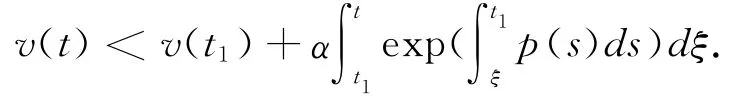
Take limit and from condition（C7），then

It contradictes v（t）≥0，so w（t）≥0.that is w（t）＝v′（t），so v′（t）≥0and v″（t）≤0.

Let

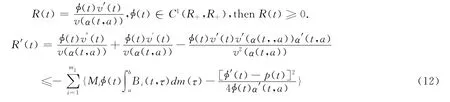
then

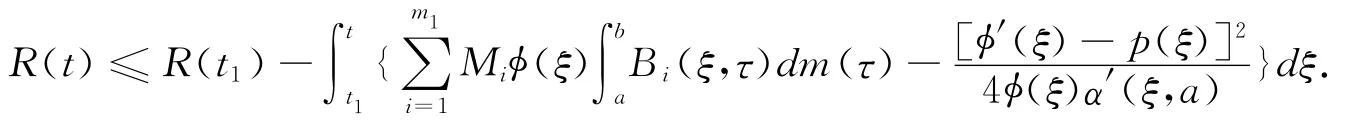
Let t→＋∞，and we combine with condition（C8），we have

It contradicts R（t）≥0.Theorem 1is proved.

Corollary 1For the equation（1），（2），the conditions（C1）—（C7）of theorem 1hold，satisfy（C′

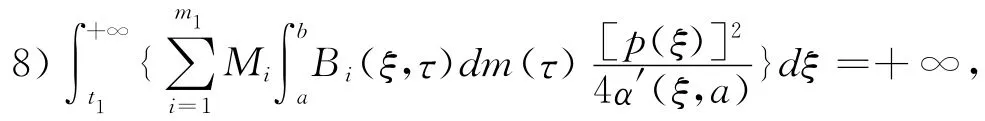
then every solution of the equation（1），（2）is oscillatory in G.

According to the proof（8）of Theorem 1，we have

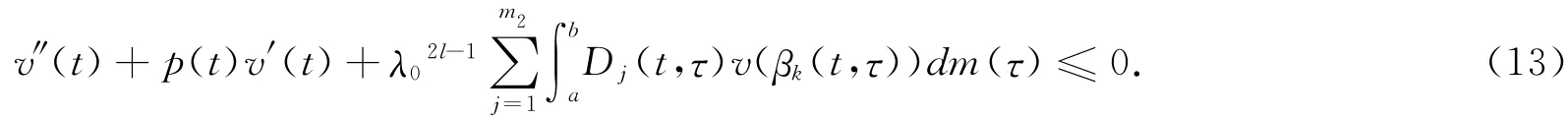
Similar to the proof of Theorem 1，we can get.

Theorem 2For the equation（1）（2），the conditions（C1）—（C7）of the Theorem 1hold，if there existed a functionφ（t）∈C1（R＋，R＋），satisfy

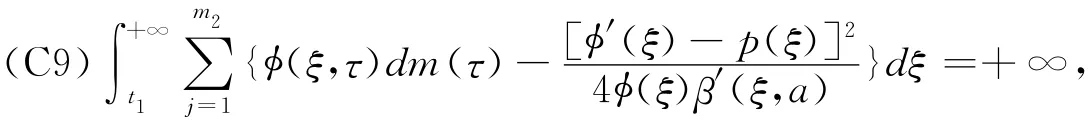
then every solution of the equation（1），（2）is oscillatory on G.

Corollary 2for the equation（1），（2），the conditions（C1）—（C7）of the Theorem 1hold，satisfy

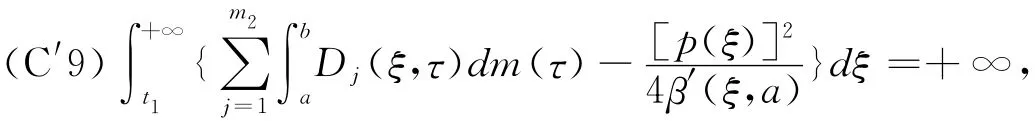
then every solution of the equation（1），（2）is oscillatory in G.

according to the proof（8）of Theorem 1，we can get

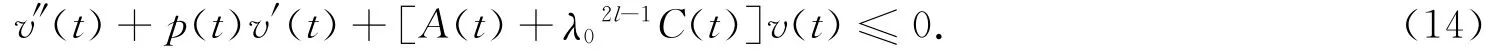
Theorem 3For the equation（1），（2）the conditions（C1）—（C7）of the Theorem 1hold，if there existed functionφ（t）∈C1（R＋，R＋），satisfy

then every solution of the equation（1），（2）is oscillatory in G.

Corollary 3For the equation（1），（2）the conditions（C1）—（C7）of the Theorem 1hold，satisfy

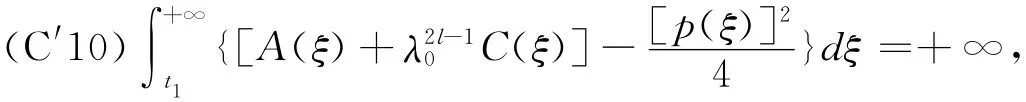
then every solution of the equation（1），（2）is oscillatory in G.

2 Conclusion

In this paper，we studied the oscillatory behaviors of the continuous delay argument hyperbolic partial differential equation with damped terms and high order Laplace operator.By using integral averaging technique and Riccati transformation，some new sufficient conditions for the oscillation of each solution of the equation are obtained in the given boundary value conditions.

［1］D P Mishev，D D Bainov.Oscillation properties of the solutions of a class of hyperbolic equations of neutral type［J］.Funkew.Ekvac，1986，29（2）：213－218.

［2］Yu Yuanhong，Cui Baotong.On the forced oscillations of solutions of hyperbolic equations with deviating arguments.Acta Mathematicae Applicatae Sinica，1994，17（3）：448－457.

［3］Cui Baotong.Oscillation properties of the solutions of hyperbolic differential equations with deviating arguments.Demonstration Math，1996，29（1）：61－68.

［4］B S Lalli，Yu Y H，Cui B T.Oscillations of hyperbolic equations with functional arguments［J］.Appl Math Comput，1993，53：97－110.

［5］Cui Baotong，Yu Yuanhong.Oscillation of certain hyperbolic delay differential equations［J］.Acta Mathematical Applicate Sinica，1996，19（3）：80－88.

［6］Yu Yuanhong，Hu Qingxi.Oscillation of solutions of partial functional differential equations with damped terms［J］.Mathematics in Practice and Theory，2000，30（3）：331－338.（in Chinese）

［7］Liu Anping.Oscillations of certain hyperbolic delay differential equations with damping terms［J］.Math Applicate，1996，9（3）：321－324.

［8］Gao Zhenghui，Luo Liping.Oscillation of the solutions of nonlinear neutral hyperbolic partial differential equation with continuous deviating arguments and damped terms.Mathematical Applicator，2008，21（2）：339－403.（in Chinese）

［9］Ye Qixiao，Li Zhengyuan.Introduction to reaction－diffusion equations［M］.Beijing：Science Press，1990.（in Chinese）