在污染環(huán)境中捕食-食餌模型的生存分析

趙堃

(東北大學信息科學與工程學院，遼寧沈陽110819)

自1926年Volterra提出著名的Lotka-Volterra微分方程模型以來，該模型已經(jīng)引起了眾多生物學家、數(shù)學家極大的興趣，并得到了許多較好的結(jié)論［1－4］.兩種群相互作用的微分方程模型 ˙x1=x1F1(x1，x2)，˙x2=x2F2(x1，x2)描述了2個種群之間的捕食與被捕食作用、相互競爭作用以及互惠作用.許多生態(tài)數(shù)學的問題都可以歸結(jié)為該模型.鑒于該模型的實際生態(tài)意義，引起了許多學者的關(guān)注.工農(nóng)業(yè)的快速發(fā)展，給當今社會帶來了莫大的好處，同時也給生態(tài)系統(tǒng)造成直接或間接的破壞影響，因此，研究污染環(huán)境中種群生存與絕滅在理論上顯得越來越重要.1984年Hallam T G等人利用數(shù)學模型定性研究毒素對生物種群生存的影響，為這一研究方向揭開了序幕，其在文獻［1］中提出的平均持續(xù)生存的概念和積分均值法，為這方面的研究奠定了基礎(chǔ).近年來，許多學者對大容量的污染環(huán)境中單種群、兩種群及三種群模型的生存與絕滅的閾值進行了研究，并取得了較好的結(jié)果［5－9］.本文在此基礎(chǔ)上研究污染環(huán)境中兩種群相互作用的微分方程模型，得到種群持續(xù)生存與絕滅的閾值，且推廣了文獻［1］中的結(jié)果.為實際應(yīng)用提供了一定的理論依據(jù).

1 模型及假設(shè)

為書寫簡潔，引入記號:

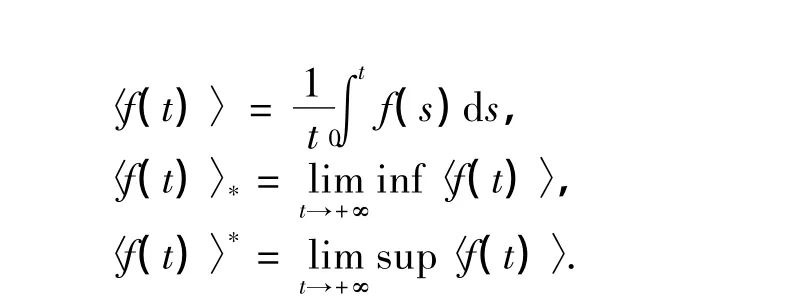
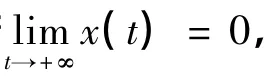
如果用xi(t)(i=1，2)、CE(t)、C0(t)分別表示t時刻2個種群的數(shù)量、環(huán)境中有害物質(zhì)的濃度、種群體內(nèi)毒素的濃度，則xi(t)(i=1，2)為有界函數(shù).取

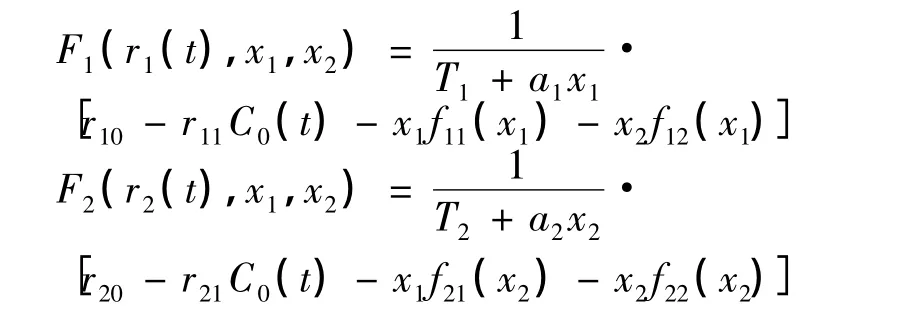
建立如下污染環(huán)境中捕食-食餌種群模型:

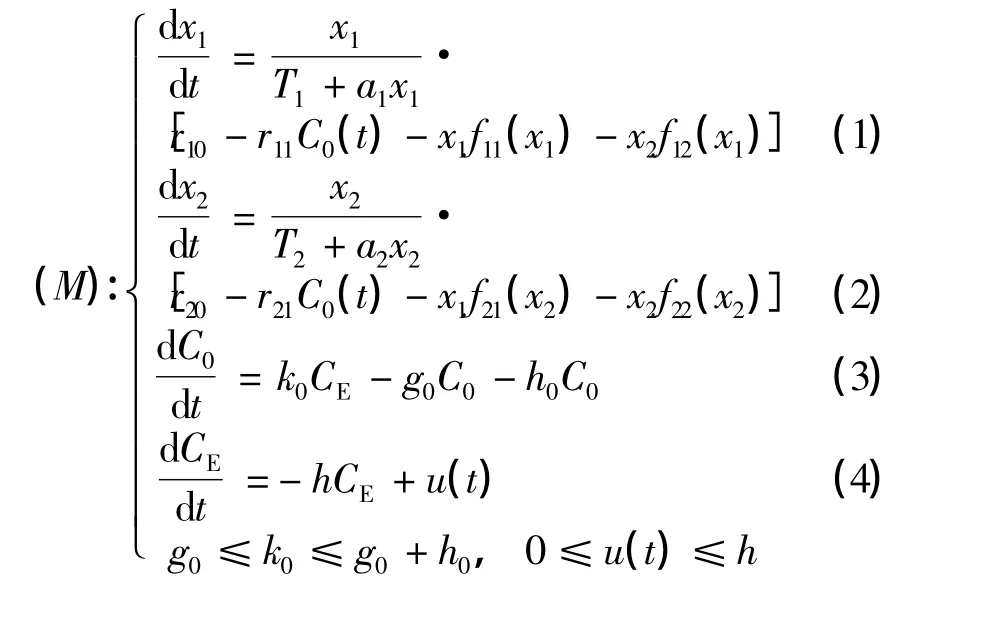
初始條件為xi0=xi(0) ＞0(i=1，2)，C0(0)≥0，CE(0)≥0.其中，ri0、ri1分別表示第i個種群的自然增長率和對毒素劑量的反映系數(shù)，連續(xù)有界量u(t)是外界向環(huán)境輸入的輸入率，且Ti＞0，ai≥0(i=1，2)，r10＞0，r20＜0，r11＞0，r21＞0，fij(xi)(i，j=1，2)均為連續(xù)函數(shù)，且mij＜fij(xi)＜Mij，M21＜0，mij＞0(i≠2，j≠1).詳情見文獻［1］.

記:Δ1=M11r20-M21r10，

Δ=M11M22-M12M21

顯然Δ＞0，~Δ1＞0.

由于從模型(M)中(3)式和(4)式可以解出C0(t)=g(u(t))，因此，尋找對u(t)的控制閾值可轉(zhuǎn)化成通過模型(1)式和(2)式尋找對C0(t)的控制閾值.

2 定理及證明

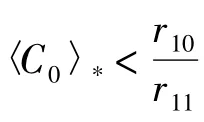
證明:由(1)式有:

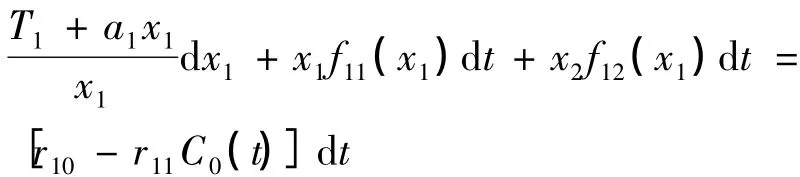
兩端積分并除以t得:

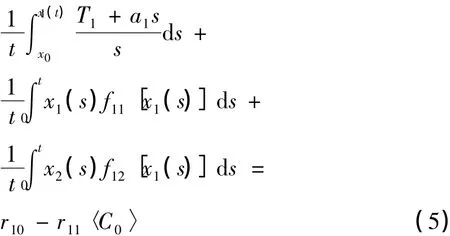
由于

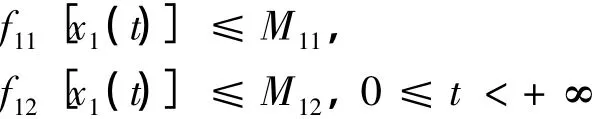
如果〈x1〉*=〈x2〉*=0，有

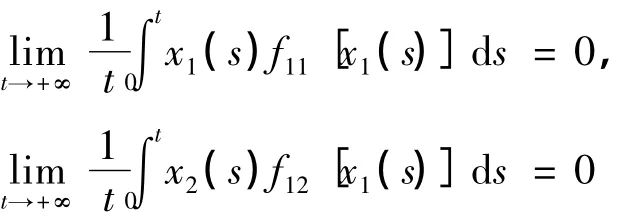
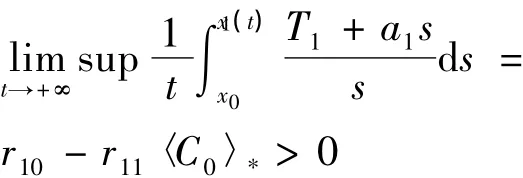
(2)由(1)式和(2)式有:

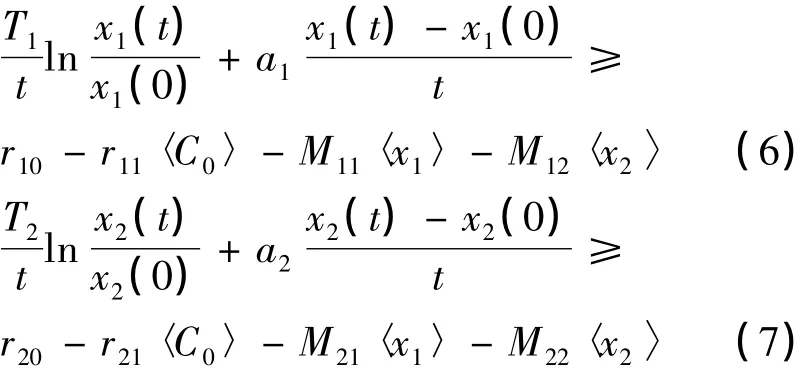
將(6)式和(7)式分別乘以-M21和M11相加得:

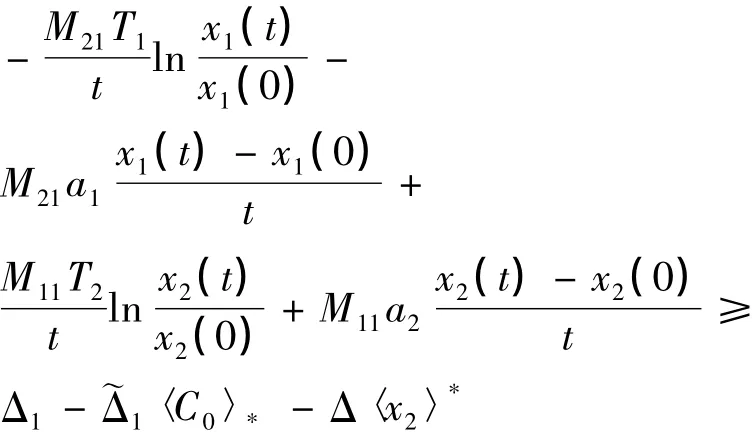
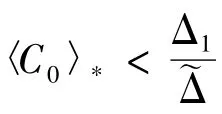
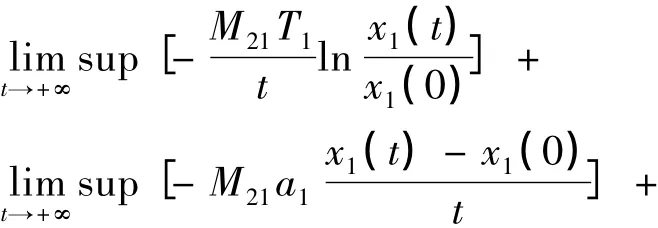
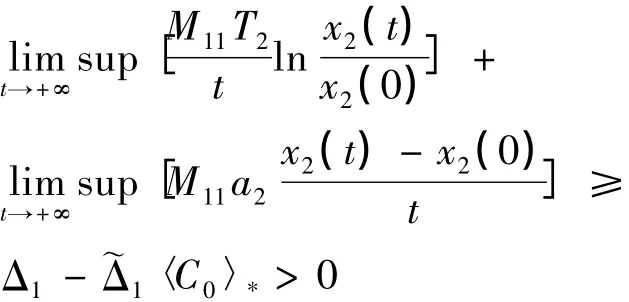
此式不可能成立，因為x1(t)與x2(t)均有界，所以必有〈x2〉*＞0.又 x1(t)的抗毒能力強于x2(t)，所以〈x1〉*＞0，即兩種群均弱平均持續(xù)生存.

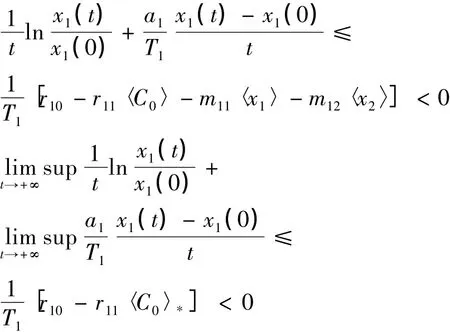
即兩種群均走向絕滅.

3 結(jié)論

在模型(M)中，當fij(xi)=aij(aii＞0，i=1，2，a12＞0，a21＜0)為常數(shù)，Ti=1(i=1，2)，ai=0時，則(1)和(2)式變?yōu)?

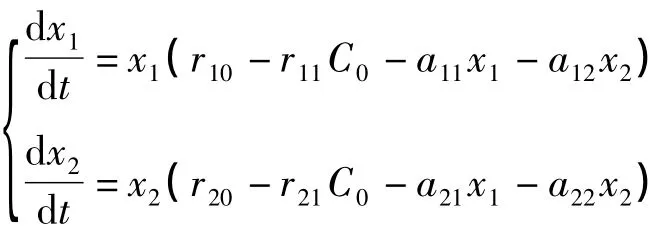
則得到與文獻［1］中相同的結(jié)論，因此，本文推廣了文獻［1］中的結(jié)果.

［1］ 馬知恩.種群生態(tài)學的數(shù)學建模與研究［M］.安徽:安徽教育出版社，1996:168－199.

［2］ 劉玉璉，傅沛仁.數(shù)學分析講義［M］.北京:高等教育出版社，1992:126－130.

［3］ 馬知恩，周義倉.常微分方程定性與穩(wěn)定性方法［M］.北京:科學出版社，2001:204－235.

［4］ 閻慧臻，馬知恩，劉燕.二維Lotka-Volterra競爭系統(tǒng)的β持續(xù)生存與 β絕滅［J］.生物數(shù)學學報，2010，25(2):294－298.

［5］ 祁延超，劉兵，張麗霞.一類污染環(huán)境中非自治捕食-食餌系統(tǒng)的持續(xù)生存與滅絕［J］.生物數(shù)學學報，2011，26(3):294－298.

［6］ 馮由玲，王克，孫靜懿.具污染與捕獲的Logistic單種群的持續(xù)生存及絕滅［J］.生物數(shù)學學報，2006，21(3):365－369.

［7］ 李長生.污染環(huán)境中兩種群的生存閾值［J］.濰坊學院學報，2004，4(2):1－2.

［8］ 靳禎.污染環(huán)境三維Volterra競爭系統(tǒng)生存與絕滅的閾值［J］.華北工學院學報，1996，13(2):201－208.

［9］ 董雨滋，王拉娣.污染環(huán)境中三維競爭系統(tǒng)的生存閾值［J］.系統(tǒng)科學與數(shù)學，1997，17(3):221－225.