一個新的簡單精確光滑罰函數

鄭芳英， 張連生

(1.上海大學理學院，上海200444;2.浙江理工大學數學科學系，杭州310018)

本研究考慮如下的約束優化問題：

式中，f，hj，gl∈C1，C1表示連續可微函數集，E，I分別表示等式約束函數以及不等式約束函數的指標集，并且E={1，2，…，m}，I={1，2，…，k}，“L-min”表示所求的問題為局部極小問題.

到目前為止，有很多方法可用于求解一般約束優化問題(P)，如序列二次規劃(sequential quadratic programming，SQP)方法、SQP信賴域法、慮子法［1］以及罰函數方法等，其中罰函數方法［2-8］是求解約束優化問題的重要途徑之一.罰函數方法是通過罰函數將約束優化問題轉化為無約束優化問題或僅含簡單約束的優化問題，從而可以利用無約束優化問題的求解算法來求解約束優化問題.傳統的罰函數，要么是簡單精確，但非光滑的，如l1精確罰函數［9］;要么是簡單光滑，但非精確的，如二次罰函數［10］;要么是精確光滑，但非簡單的，如增廣拉格朗日罰函數［11-12］.這里的“簡單”是指罰函數的表達式中僅含目標函數和約束函數，而不含其梯度信息.

通過增加一個變量，Huyer等［13］針對含箱子約束的等式約束優化問題，給出了一個新的簡單精確罰函數fσ(x，ε)，并且得到了如下結論：當σ＞0充分大及 ε＞0時，罰問題(Pσ)不存在 KKT(Karush-Kuhn-Tucher)點.特別地，對于充分大的σ＞0，具有有限目標函數值的罰問題(Pσ)的每個局部極小點(xσ，εσ)，都具有(xσ，0)形式，且xσ為原問題(P)的一個局部極小點.但在實際計算中，當ε＞0時，僅能計算罰問題的KKT點.另一方面，文獻［13］中給出的罰函數在ε=0處是不可微的，這在實際計算中會受到很多的限制.

受到文獻［13］的啟發，本研究針對一般約束優化問題(1)，給出了一個新的簡單精確光滑罰函數.在較弱的約束品性的假設下，首先證明所給出的罰函數在ε=0處是連續可微的.對充分大的罰參數σ＞0，具有有限目標函數值的罰問題(Pσ)的每個局部極小點(xσ，εσ)，都具有(xσ，0)形式，且xσ為原問題(P)的一個局部極小點.針對新的罰函數，本研究給出了兩個數值算例及計算結果，并提出了一些未來需要解決的問題.

1 一個新的簡單精確光滑罰函數

對問題(1)，定義如下集合：

式中，wj，wl∈(0，1)，j∈E，l∈I.L(P)：問題(P)的局部極小點構成的集合.顯然，S=Sε0，因此，下面的問題與問題(1)等價：

相應地，罰函數fσ(x，ε)及罰問題(Pσ)如下：

下面討論所給出的罰函數fσ(x，ε)的光滑性和精確性.

定理1 當參數α，β，γ，δ以及N滿足一定條件時，罰函數fσ(x，ε)在{(x，ε)∈Rn+1：ε=0，x∈S或者ε≠0，0＜1-cε-NδΔ(x，ε)≤1}上連續可微.

證明 記Δ(x，ε)fσ(x，ε)為fσ(x，ε)的梯度，則對任意的(x，ε)∈Rn+1，有

若ε=0，x∈S，則

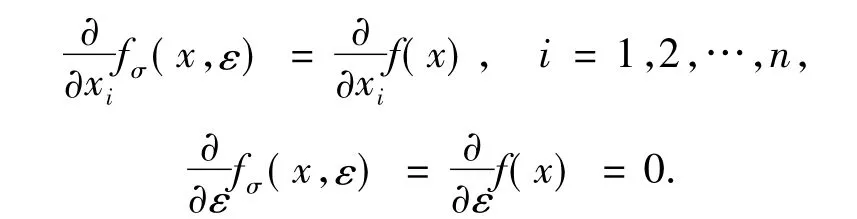
若ε≠0，0＜1-cε-NδΔ(x，ε)≤1，則

當ε≠0，0＜1-cε-NδΔ(x，ε)＜1，ε→ε*=0時，有Δ(x，ε)=O(εNδ)，從而有

整理得

當x→x*∈S，ε→0時，有

事實上，滿足式(5)的α，β，γ，δ以及N是存在的，例如取N=2，γ＞1，δ＞α，β＞1時，式(5)成立.因此，函數fσ(x，ε)在{(x，ε)∈Rn+1：ε=0，x∈S或者ε≠0，0＜1-cε-NδΔ(x，ε)≤1}上連續可微.

下面討論罰函數fσ(x，ε)的精確性，即在一定條件下，證明存在σ0＞0，當σ≥σ0時，罰函數的局部極小點具有(xσ，εσ)形式.這里εσ=0，且xσ為原問題的一個局部極小點.

引理1 如果(x(k)，εk)∈L(Pσk)，其函數值fσk(x(k)，εk)為有限值，εk≠0，且參數α，β，γ，δ，N滿足式(5)，則(x(k)，εk)?Sεk.

顯然，當εk≠0時，σkβ＞0，從而式(6)矛盾，故(x(k)，εk)?Sεk.

證明 由題設條件知

由式(8)可得

由式(7)可得

假設I+(x*，ε*)I0(x*，ε*)≠?，其I0(x*，ε*)={l：gl(x*)=ωl，l∈I}，則至少存在 l0∈I+(x*，ε*)I0(x*，ε*)，滿足gl0(x*)-ωl0＞0.根據題設，M-F約束品性在x*處成立，因此，存在p∈Rn，使得下式成立：

由式(12)，有

定理3 如果定理2的條件成立，并且參數α，β，γ，δ，N滿足相應的條件，則存在k0＞0，使得當k≥k0時，有εk=0，xk∈L(P).

即

另一方面，根據 fσ(x，ε)的定義以及函數值fσk(x(k)，0)為有限值，可知x(k)∈S.因為(x(k)，0)∈L(Pσk)，即存在(x(k)，0)的一個鄰域 o((x(k)，0)，ρk)，ρk＞0，對任意的點(x，0)∈o((x(k)，0)，ρk)，x∈S，f(x(k))=fσk(x(k)，0)≤fσk(x，0)=f(x)都成立，即x(k)∈L(P)，所以定理成立.證畢.

2 數值算例

基于軟件Matlab 7.0的環境，利用Matlab的庫函數fmincon來求解罰問題(Pσ)，從而驗證所給出的罰函數對于求解約束優化問題是有效的.表1和表2分別為兩個算例的數值結果，其中分別列出了罰參數σk，最后得到的最優解x(k)，εk以及相應的目標函數值f(x(k)).

(1)問題1.

該問題為一個二次規劃問題，存在18個局部極小值點.在該算例中，我們取α=β=2，δ=4，γ=10，ω= 0.005，N=4，選取初始點為x(0)=(0.000 0，0.000 0，0.000 0，0.000 0，0.000 0，0.000 0)，ε0=2，從而得到其中一個局部極小點為x*=(0.000 0，0.000 0，5.000 0，0.000 0，5.000 0，0.000 0)，極小值為f(x*)=-168.000 0，具體計算結果如表1所示.

(2)問題2.在該算例中，我們取α=2，β=4，δ=2，γ=2，N=4，ω=0.05，選取初始點 x(0)=(0.000 0，0.000 0，0.000 0)，ε0=2，從而得到問題2的極小點為x*= (1.000 0，-1.000 0，1.000 0)，對應的極小值為f(x*)=-7.000 0，具體計算結果如表2所示.

表1 問題1的數值結果Table 1 Numerical results of Problem 1

表2 問題2的數值結果Table 2 Numerical results of Problem 2

3 結束語

本研究得到了求解約束優化問題的一個新的方法——簡單光滑精確罰函數法.對于約束優化問題是否存在具有二次可微的簡單精確罰函數，還需要進一步的研究和探討.

［1］ FLETCHERR，LEYFFERS，TOINTP L.On the global convergence of a filter-SQP algorithm［J］.SIAM Journal on Optimization，2002，13(1)：44-59.

［2］ PILLOG D I.Exact penalty methods［M］.Netherlands：Kluwer Academic Publisher，1994：209-253.

［3］ PILLOG D I，GRIPPOL.Exact penalty functions in constrained optimization［J］.SIAM Journal on Control and Optimization，1989，27(6)：1333-1360.

［4］ PILLOG D I，GRIPPOL.An exact penalty function method with global convergence properties for nonlinear programming problems［J］.Mathematical Programming，1986，36：1-18.

［5］ PILLOG D I，LUCIDIS.An augmented Lagrangian function with improved exactness properties［J］.SIAM Journal on Optimization，2002，12(2)：376-406.

［6］ FLETCHERR.An exact penalty function for nonlinear programming with inequalities［J］. Mathematical Programming，1973，5：129-150.

［7］ FLETCHERR.Practical methods of optimization(2)：constrained optimization［M］.Wiley：John Wiley＆Sons，1981.

［8］ HANS P，MAGASARIANO L.Exact penalty functions in nonlinear programming［J］.Mathematical Programming，1979，17：251-269.

［9］ ZANGWILLW I.Nonlinear programming via penalty functions［J］.Management Science，1967，13：344-358.

［10］ FIACCOA V，MCCORMICKP.Nonlinear programming：sequential unconstrained minimization techniques［M］.Wiley：John Wiley＆Sons，1968.

［11］ HESTENESM R.Multiplier and gradient methods［J］.Journal of Optimization Theory and Applications，1969，4：303-320.

［12］ POWELLM J D.On the convergence of the variable metric algorithm ［J］.JournaloftheInstituteof Mathematics and Its Applications，1971，7：21-36.

［13］ HUYERW，NEUMAIERA.A new exact penalty function［J］.SIAM Journal on Optimization，2003，3(4)：1141-1158.