基于一種新的γ-擴張凹極小化問題的割平面算法

2012-01-31 06:05:22劉林娜楊永建

上海大學學報(自然科學版) 2012年1期

劉林娜，楊永建，余峰

(上海大學理學院，上海200444)

近年來，人們已經較為深入地研究了凸規劃問題，并且給出的方法大多非常有效［1］.但是，對于在生活中有著很強實際應用背景的一些問題，如金融經濟［2-3］、工程設計和非線性系統的魯棒穩定性分析［4］等卻只能表示為非凸規劃問題.雖然非凸二次規劃問題是困難的多極值全局優化問題，但仍有不少學者在這方面取得了一定的進展［5-8］.本工作主要研究一類特殊的非凸二次規劃問題——凹極小化問題.凹極小化問題是一種比較常見的多極值優化問題，在全局優化領域有著重要的應用.許多類型的優化問題，如0-1整數規劃問題、雙線性規劃問題、互補問題和某些乘積問題等都可以轉化為等價的凹極小化問題.如

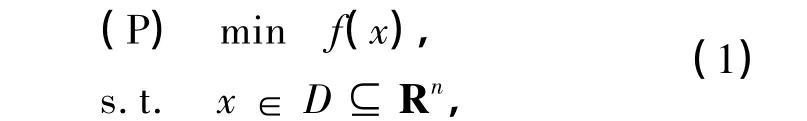
式中，f(x)∶Rn→R在非空集合D上是凹的，D為Rn中非空凸集(假設D為多面體).事實上，如果問題(P)的最優值不是∝，則一定可以在D的頂點處找到一點，使f(x)在該點取到最優值，即凹函數在多胞形上的全局極小值一定是在多胞形的某個頂點取到，并稱該性質為極點最優性.進一步來說，當可行域為緊凸集時，凹函數的極點最優性仍然成立.本工作先作以下2個假設.

假設1 凹函數f(x)：D→R可延拓到F(x)：Rn→R，且F(x)為可微函數.

假設2 凸集D為多胞形，且有非退化的頂點，即int D≠?.

下面對以上假設作進一步說明.

命題1 令D?Rn是凸的，int D≠?，f：D→R

在D上是凹函數，并且是連續的.假設‖Δf(x)‖在集合DΔ={x∈D：f(x)在x點是可微的}上是有界的，其中 Δf表示 f的梯度，‖·‖為歐幾里得范數，則

在Rn上是凹的，且在D上，有F(x)=f(x).

證明對任意的y∈DΔ，令

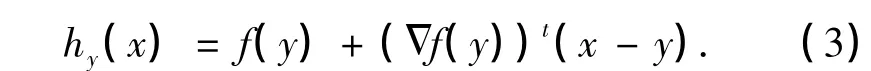
對于每個y，hy是仿射的，F(x)是仿射函數的下確界，所以F(x)在Rn上是凹的.對于所有的x，y∈DΔ，hy(x)≥f(x).在DΔ上，有hx(x)=f(x)，因此，F(x)=f(x).由于DΔ在int D內是稠密的，根據f在D上的連續性可知，在D上有F(x)=f(x).

假設D是多胞形，且int D≠?，顯然等價于dim D=n.若dim D=d＜n，則可以在一個包含D的d維空間內進行討論.

割平面的概念是由Gomory在1958年首先提出用來構造整數規劃的算法.Gomory割平面是通過不斷求解其線性規劃松弛形式，構造合適的割平面，從而去掉松弛形式的非整數解，最終找到一個整數向量的最優解.該算法能夠保證整數規劃在有限步內求得最優解.后來，Tuy［8］又提出了一種求解凹極小化問題的割平面，其中心思想是：基于以上2條假設，易求得可行域D的一些可行點，通過傳統的線性規劃算法(如單純形方法)可以找到D的一個頂點v1.由f(x)的可微性可知，D的發自v1的邊方向d，由此可找到滿足dtΔf(v1)＜0的方向d.對于v1的鄰點v2=v1+ λd，可根據f(x)的凹性，即f(v2)≤f(v1)+(v2－v1)t· Δf(v1)(由于(v2－v1)tΔf(v1)＜0，且f(v2)＜f(v1))，通過轉軸方法或者標準的非線性規劃的局部算法，總可以找到f(x)在D上的一個局部極小點x0.令γ=f(x0)≥min{f(x)：x∈D}，由此構造超平面H，一般稱之為割或者割平面，使得對于所有的x∈D∩H－，有f(x)≥γ，即試圖通過割掉一部分可行域，來保證該部分上的目標函數值不小于f(x0).若可行域剩下的部分不為空集，則可用同樣的方法應用到剩余部分.

1 變上限積分函數方法

考慮變上限積分函數［9］

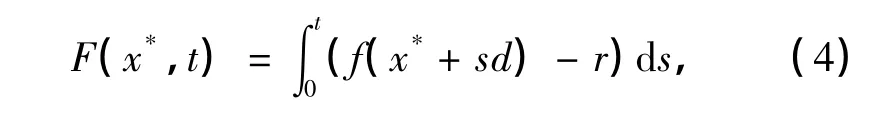
式中，x*為f(x)在可行域D上的局部極小點，d是一個已知方向，r=f(x*)是局部極小值.若f(x)為強制函數，則F(x*，t)也為強制函數.下面給出F(x*，t)的一些性質.

定理1 設x*是f(x)的一個局部極小點，若f(x)在以 x*為起點，以 d為方向的射線上恒有f(x)≥r，即對于任意的s≥0，有f(x*+sd)≥r，那么函數F(x*，t)是一個關于t的增函數.

證明對函數F(x*，t)求導，可得

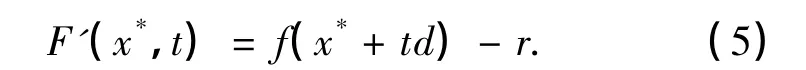
由條件f(x)≥r可知，F'(x*，t)≥0，故F(x*，t)是關于t的增函數.

定理2 設x*是f(x)的一個局部極小點，若f(x)在以x*為起點，以d為方向的射線上存在函數值小于r的點x，那么在該射線上一定存在一點x0，使得f(x0)=r，并使得對應的t0是函數F(x*，t)的局部極大點，其中x0=x*+t0d.

證明假設在射線上存在一點x'，使得f(x')＜r.因為f(x)連續，由介值性定理可知，在該射線上一定存在一點x0，使得

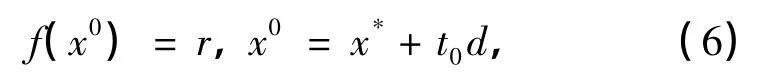
并且存在t0的一個鄰域(t0－δ，t0+δ)(δ＞0)，使得當t∈(t0－δ，t0］時，f(x*+td)≥r;當t∈(t0，t0+δ)時，f(x*+td)≤r.

任取t∈(t0－δ，t0］，有

任取t∈(t0，t0+δ)，有

故t0為函數F(x*，t)的局部極大點.

定理3 設x*是f(x)的一個局部極小點，對于某個方向d，若t*是函數F(x*，t)的一個平穩點，則有f(x*+t*d)=r.

證明對函數F(x*，t)求導，得到

由于t*是F(x*，t)的穩定點，則有

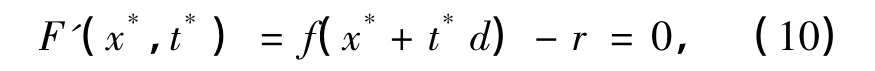
即有f(x*+t*d)=r.

下面，考慮問題

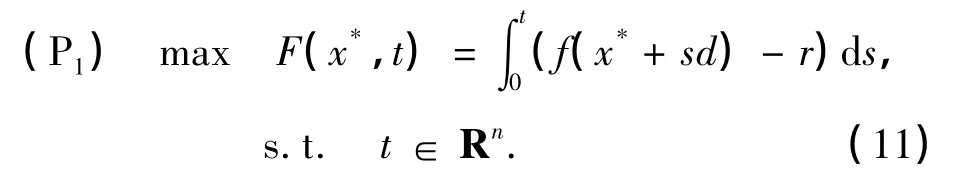
可以利用局部算法來求解問題(P1)，這里采用Newton算法，算法步驟如下.

步驟1 初始化.給定初始點tk，誤差控制?＞0，記k=0.

步驟4 迭代改進.通過線搜索確定步長參數αk，令tk+1=tk+αkek，置k+1→k，轉步驟2.算法終止.

Newton算法比最速下降法的收斂速度要快，固定步長αk=1，則迭代產生的序列{tk}是收斂于點t*的，且為二階收斂.通過Newton算法可以找到問題(P1)的極大點t*.

2 割平面算法

首先，假設凹極小化問題(P)的可行域

是非空閉凸集，式中，A為m×n階矩陣，b為歐式空間的n維向量.通過傳統的線性規劃(如單純形法)可求出 f在 D上的一個局部極小點 x0.顯然有f(x0)≥min{f(x)：x∈D}，令γ=f(x0)，我們感興趣的區域為D(γ)=D∩{x∈Rn|f(x)＜γ}.在求解凹極小化問題的算法中，首要任務是在以x為起點，d為方向的射線ρ(x，d)={y：y=x+td，t≥0}上找到最長的線段［x，x+t*d］，使得對所有的y∈［x，x+ t*d］，有f(x)≥γ.特別地，γ是在極小化過程中的某一階段得到的最佳目標函數值.在區間［x，x+t*d］中，不會有比當前局部最優值更佳的最優值.若f(x)為嚴格凹的，且上水平集L(f(x);γ)={x：f(x)≥γ}有界，則y=x+t*d是射線ρ(x，d)與L(f(x);γ)的邊界的交.若L(f(x);γ)沿d無界，則t*=+∝，即在整個射線ρ(x，d)上有f(y)≥γ，這時一般取t*=t1，其中t1為充分大的正數.

下面給出γ-擴張的定義.

定義1 令f：Rn→R是凹函數，x∈Rn，γ是滿足γ≤f(x)的實數，并且t1＞0充分大.稱點y∈Rn為x沿方向d∈Rn