改進的隱式空間映射算法的研究

孫培展，袁國良

（上海海事大學 信息工程學院，上海 201306）

空間映射算法[1-2]在微波工程中得到實際驗證，目前已成功應用于微波濾波器、微波天線、功分器等微波器件的設計中。空間映射算法有效將將粗糙模型的快速性和精細模型的精確性結合起來，將費時的精細模型優化計算轉變為不費時的粗糙模型迭代優化計算。

為了空間映射算法準確應用，得到一個合適的方法，使粗糙模型的響應高效準確逼近精細模型的響應，一直是需要解決的問題。

文中介紹了限定參數提取隱式空間映射算法[3]，通過減少粗糙模型的參數空間而實現粗糙模型響應高效準確逼近精細模型響應。最后得到的空間映射算法的性能在收斂特性和優化設計質量方面都得到改善。文中通過設計一個交叉耦合濾波器，將新算法和舊算法的計算結果和逼近速度進行比較，結果新算法更快地滿足了設計指標要求，并且優化得到了比指標要求更優越的結果，加快了精細模型逼近目標的速度，提高了優化效率，為微波器件的設計節省了大量寶貴的時間。

1 隱式空間映射

設點xf的精細模型響應Rf（xf），初始問題即是求解式[4-6]

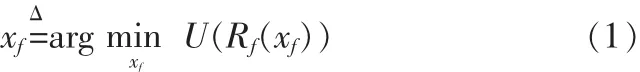
其中，U是一個給定的目標函數，xf是需要求解的精細模型參數。

在j步迭代中，設x（j）c為粗糙模型的優化參數變量，x（j）為優化輔助參數（即參數提取時進行優化的參數，以使粗糙模型響應逼近精細模型響應），則Rc（x（j）c，x（j））為相應的粗糙模型響應。

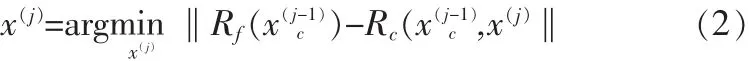
其中，‖·‖表示一個適當的范數。優化參數x的這個過程叫做參數提取過程。

參數提取過程完成后，優化粗糙模型得到：

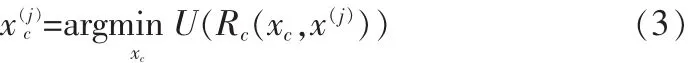
優化得到的粗糙模型參數x(j)c直接代入精細模型進行電磁計算：

若精細模型的響應滿足設計要求，則整個優化過程完成。否則再次進行參數提取，然后優化粗糙模型，如此循環優化直到精細模型的響應滿足設計目標。

2 限定空間映射

文中在傳統的隱式空間隱式算法基礎上，通過限定參數提取算法，實現粗糙模型響應高效準確逼近精細模型響應。為了粗糙模型能夠足夠準確逼近精細模型，這準確性在特定的迭代點，使用合適的標準來測量，例如，ε（i）=‖Rf（）-Rc（）‖。為了ε（i）足夠小，設置ε（i）≤εmax（εmax是用戶設定的臨界值），以便迭代后的粗糙模型能很好的匹配Rf。

2.1 適當的限制參數提取

根據文獻[4]提出的算法，參數提取過程（2）由下面的公式代替：

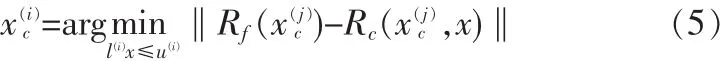
l（i）和 u（i）分別是迭代為 i的提前設定參數的上邊界和下邊界。 這里假設 l（i）=x（i－1）－δ（i）和 u（i）=x（i－1）－δ（i），x（0）是提前設定參數的初始值 ，δ（i）為代表參數空間大小的變量 （δ（0）為 自定義 初始值）。

有限參數提取流程如下：

1）計算 l（i）=x（i－1）－δ（i）和 u（i）=x（i－1）+δ（i）；

2）用（7）得到 x（i）；

3）如果ε（i）≤αdecr·εmax，那么δ（i+1）=δ（i）/βdecr，跳到步驟6）；

4）如果ε（i）＞αincr·εmax，那么δ（i+1）=δ（i）·βincr，跳到步驟6）；

5）設置 δ（i+1）=δ（i）；

6）結束。

αdecr，αincr，βdecr和 βincr是用戶自定義參數 （典型值：αdecr=1，αincr=2，βdecr=5，βincr=2）。

2.2 限制代理模型優化

空間映射算法的收斂特性可以通過限制粗糙模型（3）明確控制，公式表達變更為：

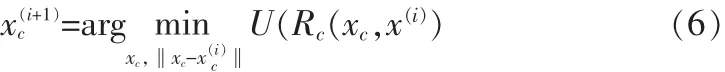
δ（i）=α‖x‖，α＜1(推薦α=0.6～0.9)。α如果太小，可能導致提前收斂，沒有發現滿意的設計。限制優化粗糙模型有助于在x（i）c的閉區域內快速發現合適參數。

3 交叉耦合濾波器設計實例

文中運用交叉耦合濾波器的設計實例[7]驗證限制參數空間映射算法的優越性。交叉耦合濾波器的優化目標|S11|＜－20 dB，0.88 GHz≤w≤0.92 GHz和|S21|＜－35 dB，w＜0.82 GHz且|S21|＜－15 dB，w＞1 GHz。此交叉耦合濾波器選定氧化鋁陶瓷片為微帶濾波器的介質基板，其相對介電常數為εγ=9.6，介質厚度為h=1.27 mm。

設置各個耦合線的介質層的材料和厚度為參數提取變量x。

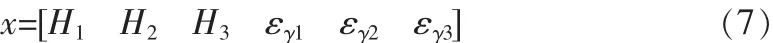
粗糙模型優化變量為濾波器各腔的長度、腔與腔之間的耦合間距，耦合腔的開口尺寸等，設為：

粗糙模型初始參數分別為xc=[22.2 7.2 2 0.4 1.4 0.5]，x=[1.27 1.27 1.27 9.6 9.6 9.6]，參數空間大小的變量初始值為 δ（0）=[1 1 1 2 2 2]。

將粗糙模型優化參數xc導入Ansoft HFSS計算精細模型，精細模型如圖1所示[8]。

圖1 交叉耦合濾波器精細模型Fig.1 Fine model of cross-coupled filter

初始精細模型計算結果如圖2（a）所示，初始模型的通帶向右偏移，需要進一步迭代優化。在迭代中，采用上文中介紹的限定參數提取隱式空間映射算法，第1步迭代HFSS計算結果對照如圖(b)所示，頻帶基本達到了技術要求的頻帶，但帶內衰減和帶外抑制指標沒有滿足要求。第2步迭代結果如圖(c)所示，精細模型響應更近指標要求。第3步迭代結果如圖(d)所示，帶外抑制指標達到要求，帶內衰減指標尚且不能滿足。第4步迭代結果如圖（e）所示，帶內衰減和帶外抑制指標都已經滿足。

圖2 結果的圖片示例Fig.2 Picture examples of results

限定參數提取空間映射算法和未改進的空間映射算法之間得到最優參數的迭代次數的比較如圖3所示。表1為限定參數提取空間映射算法和未改進的空間映射算法的通帶內衰減比較結果。通過結果可以發現限定參數提取空間映射算法收斂速率明顯比未改進的空間映射算法的收斂速率快，更高效地得到最優參數。

圖3 ‖‖的迭代比較結果Fig.3 Iteration results of the comparison of‖‖

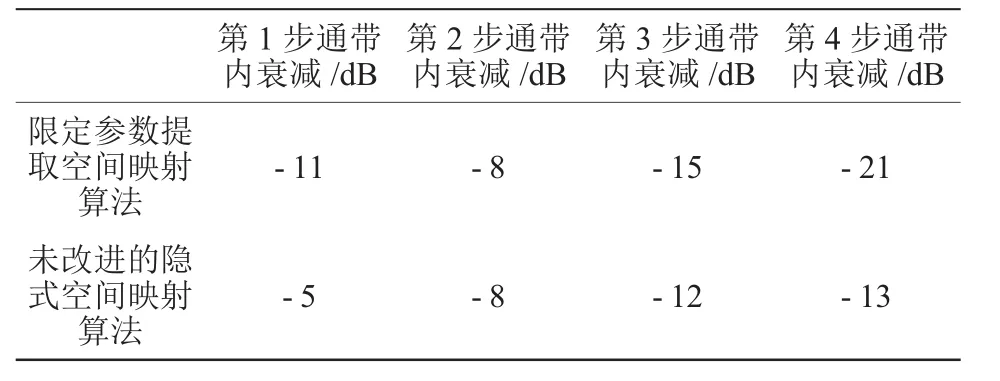
表1 通帶內衰減比較結果Tab.1 Results of the comparison of passband attenuation

4 結 論

文中介紹了限定參數提取隱式空間算法，有效減少選擇代理模型參數的問題，提高收斂特性和空間映射優化過程的整體特性，改進了粗糙模型和精細模型的映射關系，減少細模型的計算次數，優化出的精細模型結果逼近指標速度大大加快，提高了優化效率，為微波器件的設計節省了寶貴時間。

[1]Bandler JW，CHENGQS，Dakroury SA.Space mapping:the state of the art[J].IEEE Transactions on Microwave Theory and Techniques，2004，52（1）:337-361.

[2]Bandler J W，Biernacki R M，CHEN Shao-hua，et al.Space mapping technique for electromagnetic optimization[J].IEEE Transactions on Microwave Theory and Techniques，1994，42（12）:2536-2544.

[3]Koziel S，Bandler J W，CHENG Q S.Adaptively constrained parameter extraction for robust space mapping optimization of microwave circuits[J].IEEE MTT-SInt.Microwave Symp，2010，5（1）:205-208.

[4]Bandler JW，CHENGQS，Nikolova N K，et al.Implicit space mapping optimization exploiting preassigned parameters[J].IEEE Transactions on Microwave Theory and Techniques，2004，52（1）:378-385.

[5]CHENG Q S，Bandler J W，Koziel S，et al.Combining coarse and fine models for optimal design[J].IEEE Microwave Magazine，2008，9（1）:79-88.

[6]Koziel S，Bandler J W，Madsen K.Quality assessment of coarse models and surrogates for space mapping optimization[J].Optimization and Engineering， 2008，9(4):375-391.

[7]Brady D.The design，fabrication and measurement of microstrip filter and coupler circuits[J].High Frequency Electronics，2002，4（7）:22-30.

[8]謝擁軍，劉瑩，李磊，等.HFSS原理與工程應用[M].北京：科學出版社，2009.