負(fù)偏心對(duì)鋼管－插板K型節(jié)點(diǎn)承載力的影響

王蔚佳，劉紅軍，李正良

（重慶大學(xué)土木工程學(xué)院，重慶 400045）

負(fù)偏心對(duì)鋼管－插板K型節(jié)點(diǎn)承載力的影響

王蔚佳，劉紅軍，李正良

（重慶大學(xué)土木工程學(xué)院，重慶 400045）

對(duì)主管規(guī)格為219 mm×6 mm有負(fù)偏心作用的1／4加肋鋼管插板連接的極限承載力進(jìn)行了試驗(yàn)研究，根據(jù)試驗(yàn)結(jié)果提出了等效受力模型，在此基礎(chǔ)上研究了有負(fù)偏心的1／4（1／2）和全環(huán)形加強(qiáng)板鋼管插板連接的K型節(jié)點(diǎn)的主管軸力、主管管壁彎矩和剪力三者之間的相互關(guān)系，并利用有限元軟件分析了各參數(shù)對(duì)節(jié)點(diǎn)極限承載力的影響，在此基礎(chǔ)上提出了此類節(jié)點(diǎn)的建議公式并與試驗(yàn)結(jié)果進(jìn)行了比較。結(jié)果表明：建議公式表面看是反映兩兩之間的相互關(guān)系，實(shí)際上是反映了主管軸力、主管管壁彎矩和剪力三者之間的關(guān)系，建議公式能較好的估算節(jié)點(diǎn)承載力的上限值。

負(fù)偏心；極限承載力；插板連接；等效受力模型

鋼管塔構(gòu)造中斜材軸心線交于主材軸心線造成節(jié)點(diǎn)板尺寸很大，節(jié)點(diǎn)連接負(fù)偏心可以減小節(jié)點(diǎn)板尺寸，減小迎風(fēng)面積。然而，在目前的設(shè)計(jì)中［1－8］，由于其復(fù)雜的受力形式，插板連接的極限承載力建議公式僅適用于有限的情況。許多學(xué)者提出的建議公式都是針對(duì)無(wú)偏心的情況。Kurobane［9］通過(guò)試驗(yàn)研究了在軸力和彎矩作用下T型和X型節(jié)點(diǎn)的極限承載力；Wardenier、Packer等［10－12］針對(duì)單插板和雙插板連接提出了建議公式；Ariyoshi等［13］確立了圓鋼管與插板連接在簡(jiǎn)單荷載作用下的試驗(yàn)結(jié)果和數(shù)值分析結(jié)果的數(shù)據(jù)庫(kù)。但他們都沒(méi)有考慮主管和支管上荷載的聯(lián)合作用效應(yīng)以及偏心對(duì)極限承載力的影響。

Kim等［14－16］對(duì)無(wú)環(huán)形加強(qiáng)板情況下偏心對(duì)極限承載力的影響進(jìn)行了初步研究。由于K型節(jié)點(diǎn)受力的復(fù)雜性，尤其是鋼管－插板連接的K型節(jié)點(diǎn)受力更加復(fù)雜，所以關(guān)于K型節(jié)點(diǎn)的極限承載力公式很少。為進(jìn)一步研究負(fù)偏心對(duì)K型節(jié)點(diǎn)承載力的影響，筆者通過(guò)試驗(yàn)及有限元軟件對(duì)負(fù)偏心鋼管塔節(jié)點(diǎn)承載力進(jìn)行了研究，提出了計(jì)算此類節(jié)點(diǎn)的建議公式。

1 試驗(yàn)研究

1.1 試驗(yàn)試件及加載裝置

試驗(yàn)研究4種不同插板連接的節(jié)點(diǎn)，主要考察偏心距對(duì)主管極限承載力的影響和局部應(yīng)力集中現(xiàn)象。各試件參數(shù)見(jiàn)表1。為了防止節(jié)點(diǎn)板發(fā)生破壞，節(jié)點(diǎn)板的厚度都比較大。試驗(yàn)主要研究不同參數(shù)情況下節(jié)點(diǎn)的破壞類型并比較偏心距對(duì)主管承載力的影響。插板連接構(gòu)造如圖1所示，加載裝置如圖2所示，環(huán)板的形式如圖3所示。

1.2 加載方案

試驗(yàn)加載為單向加載。主管與支管同步加載，1＃千斤頂（拉）和3＃千斤頂（壓）分別與支管相連，2＃千斤頂與主管相連，見(jiàn)圖2。支管荷載先以每級(jí)荷載增量為25 k N逐級(jí)加載至250 k N，而主管荷載以每級(jí)荷載增量為40 k N逐級(jí)加載至400 k N；后支管以每級(jí)荷載增量為10 k N逐級(jí)加載至350 k N，而主管荷載以每級(jí)荷載增量為20 k N逐級(jí)加載至600 k N；最后支管以每級(jí)荷載增量為5 k N逐級(jí)加載至支管受壓承載力而停止加載，而主管荷載以每級(jí)荷載增量為5 k N逐級(jí)加載至構(gòu)件破壞。此時(shí)主管的荷載即為主管的極限承載力，每級(jí)加載停頓1 min后繼續(xù)加載。

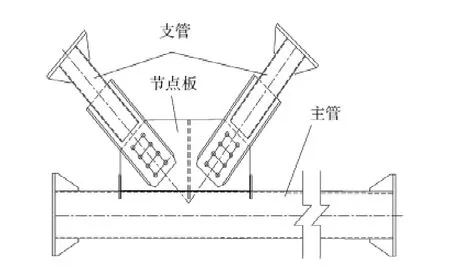
圖1 插板連接構(gòu)造圖

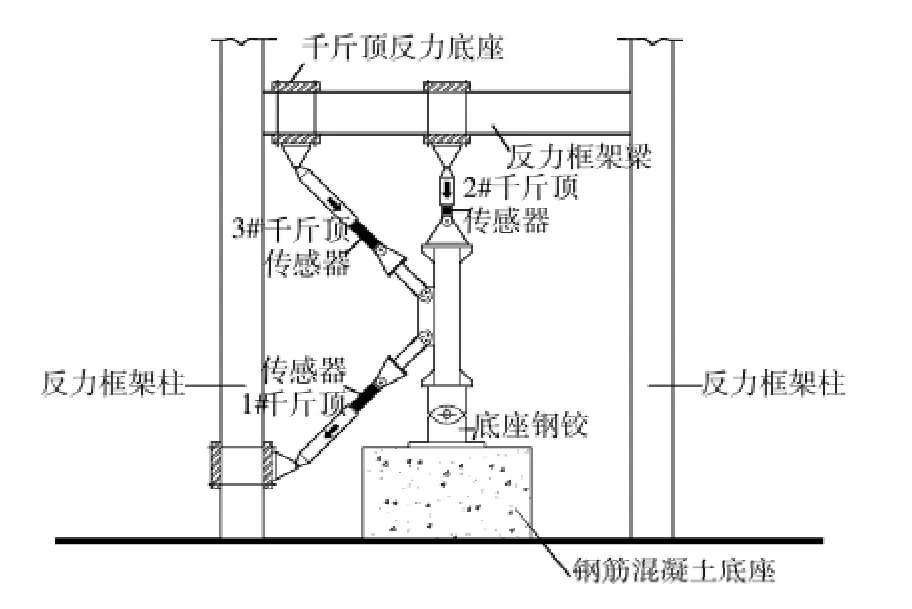
圖2 試驗(yàn)裝置圖

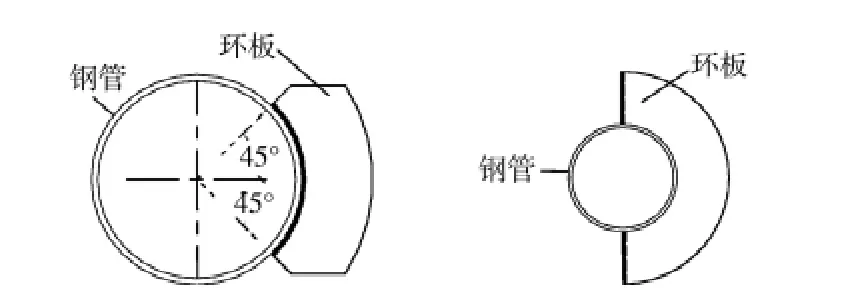
圖3 1／4（1／2）環(huán)板連接構(gòu)造圖

1.3 試驗(yàn)結(jié)果

試驗(yàn)結(jié)果表明：構(gòu)件發(fā)生整體失穩(wěn)先于局部屈曲。主要原因在于主管長(zhǎng)徑比較大，屬于壓彎構(gòu)件，整體很容易失穩(wěn)。由于主管長(zhǎng)徑比較大，因此整體失穩(wěn)起主要控制作用，負(fù)偏心加速了整體失穩(wěn)，降低了主管的承載能力。因此負(fù)偏心對(duì)整體失穩(wěn)不利。表2為不同支管荷載作用下的主管承載力。

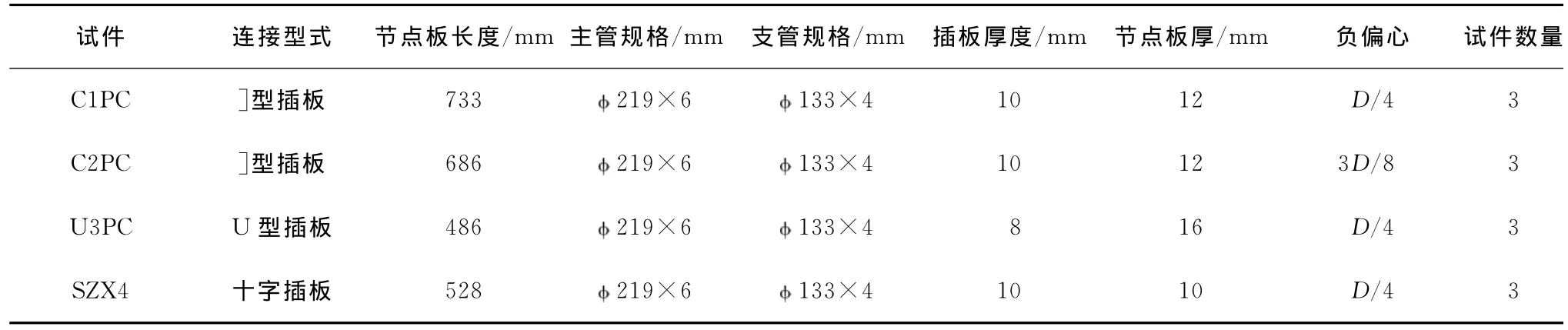
表1 各試件參數(shù)

表2 試驗(yàn)結(jié)果

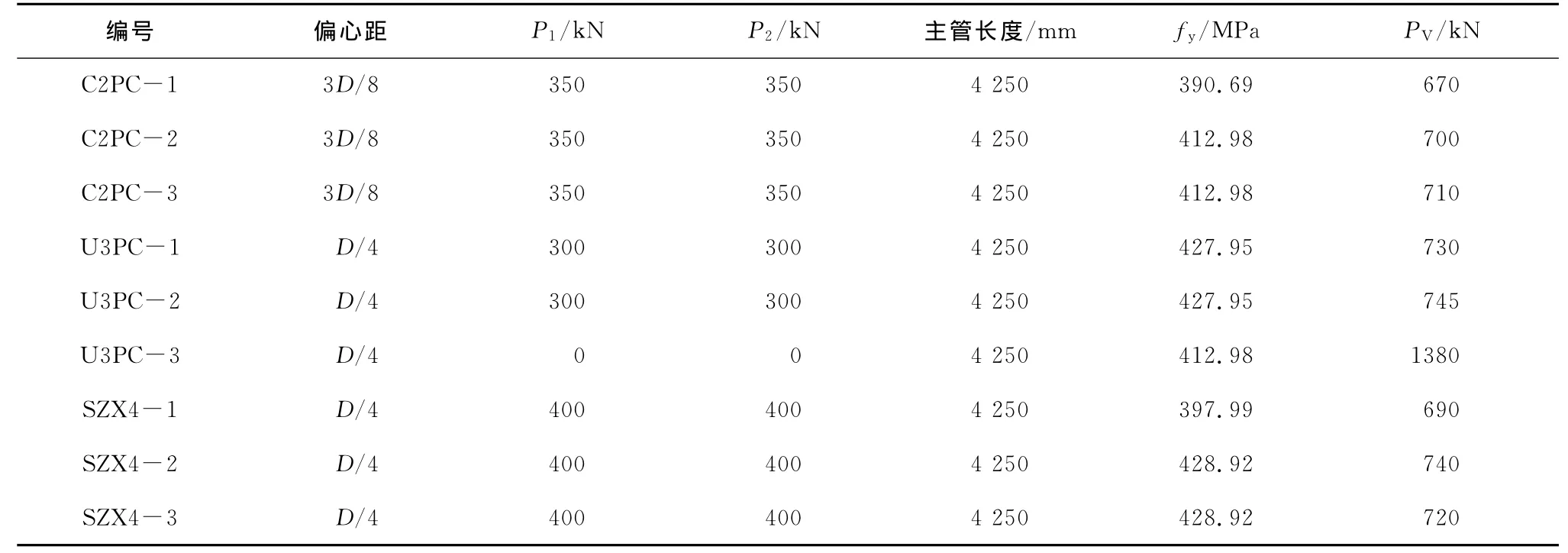
續(xù)表2

2 節(jié)點(diǎn)等效受力模型

在輸電塔架結(jié)構(gòu)中，K型節(jié)點(diǎn)經(jīng)常用于主材與斜材的連接，見(jiàn)圖4。通過(guò)對(duì)K型節(jié)點(diǎn)受力分析發(fā)現(xiàn)，支管荷載對(duì)主管管壁的作用可以分解成彎矩和剪力，如圖5所示。

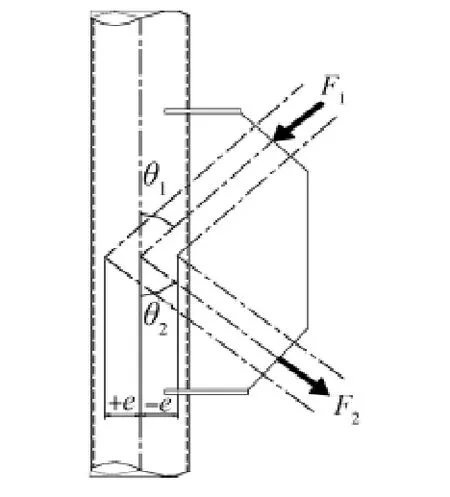
圖4 K型節(jié)點(diǎn)的構(gòu)造圖

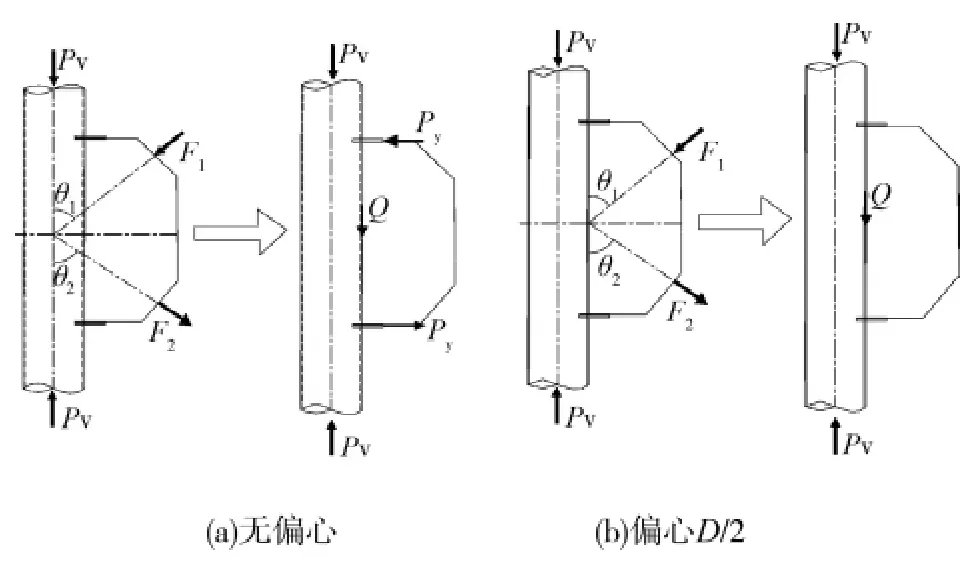
圖5 節(jié)點(diǎn)等效受力模型

既然中空?qǐng)A形截面在外荷載作用下更容易發(fā)生局部變形，那么K型節(jié)點(diǎn)構(gòu)造的幾何尺寸就應(yīng)該通過(guò)精確分析確定。但由于受力性能的復(fù)雜性，目前的設(shè)計(jì)規(guī)范沒(méi)有詳細(xì)的公式，因此，基于負(fù)偏心作用的K型節(jié)點(diǎn)的極限承載力的研究很有必要。

筆者利用有限元程序ANSYS對(duì)K型鋼管－插板連接節(jié)點(diǎn)進(jìn)行彈塑性大撓度分析，研究節(jié)點(diǎn)的應(yīng)力分布情況和極限承載力，其模型見(jiàn)圖6。模型分析中采用4節(jié)點(diǎn)四邊形殼單元shell181來(lái)模擬節(jié)點(diǎn)板、鋼管和加強(qiáng)板。邊界條件如圖7所示，主管一端按固定支座考慮，另外一端為僅有沿主管軸線方向位移的固定支座。兩支管端部邊界為滑動(dòng)鉸支座，僅允許沿管軸線方向有位移，約束徑向位移。加載方式與試驗(yàn)相同。有限元分析時(shí)，材料選取Q345，其屈服強(qiáng)度f(wàn)y＝345 MPa，在考慮材料非線性時(shí)，從材料的單軸拉伸試驗(yàn)曲線中得到，其應(yīng)力－應(yīng)變關(guān)系如圖8所示。彈性模量E＝2.06×105MPa，泊松比取0.3，忽略自重的影響。表3即為試驗(yàn)結(jié)果與有限元結(jié)果的比較。從表3可以看出，計(jì)算結(jié)果與試驗(yàn)結(jié)果較接近，吻合性較高，具有較好的適用性。

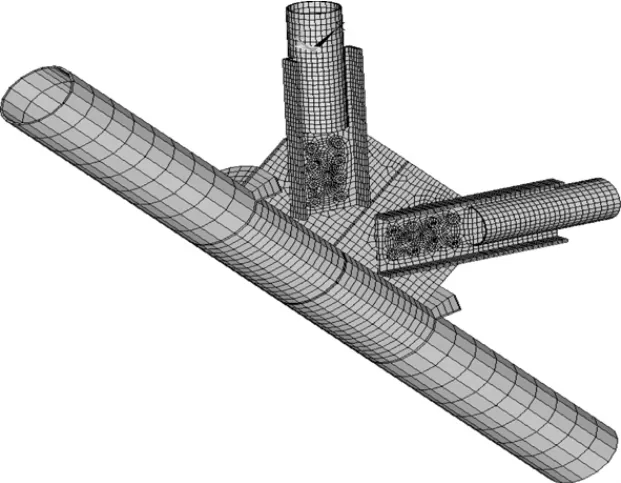
圖6 有限元模型

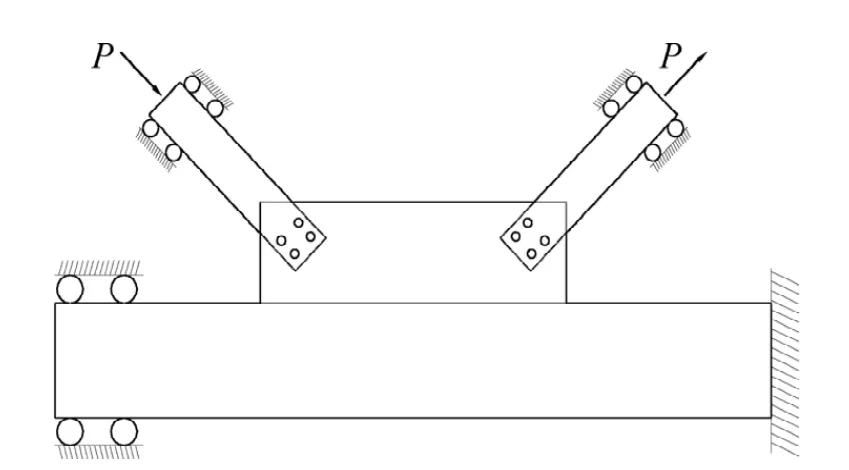
圖7 節(jié)點(diǎn)加載示意圖

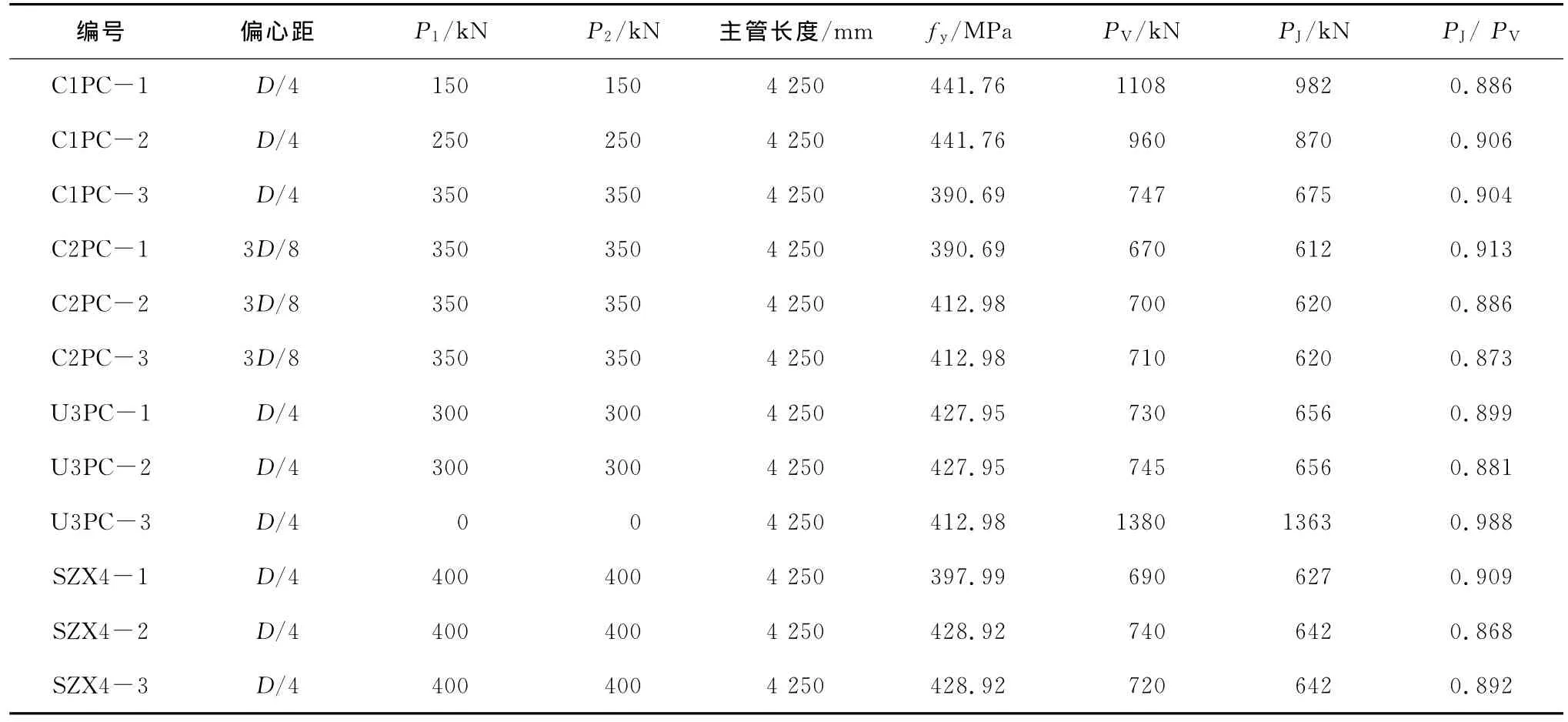
表3 試驗(yàn)結(jié)果

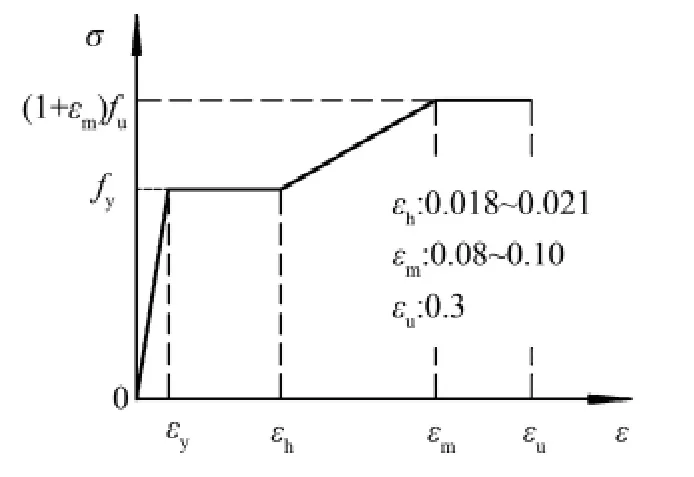
圖8 材料應(yīng)力－應(yīng)變關(guān)系模型

3 參數(shù)對(duì)承載力的影響

通過(guò)有限元軟件對(duì)1／4（1／2）和全圓環(huán)加強(qiáng)板K型節(jié)點(diǎn)各參數(shù)對(duì)節(jié)點(diǎn)承載力的影響進(jìn)行了分析，其關(guān)系曲線如圖9所示。

從圖9可以看出，節(jié)點(diǎn)在無(wú)偏心的情況下，主管直徑D和主管壁厚t對(duì)節(jié)點(diǎn)承載力有顯著影響。節(jié)點(diǎn)承載力隨著節(jié)點(diǎn)板高度B的增加變化甚微，幾乎不變；主管管壁彎矩（M＝Py·B）隨著環(huán)形加強(qiáng)板高度和厚度的增加而增加，其變化趨勢(shì)較平緩。在偏心距為D／2的情況下，主管管壁剪力隨著主管直徑的增加而線性增加；隨著主管壁厚的增加也呈線性增加趨勢(shì)；而節(jié)點(diǎn)板高度、加強(qiáng)板高度和加強(qiáng)板厚度對(duì)主管管壁剪力的影響甚微，幾乎不變，表明在偏心距為D／2時(shí)剪力只對(duì)主管發(fā)生局部屈曲時(shí)產(chǎn)生作用。

4 節(jié)點(diǎn)承載力實(shí)用計(jì)算方法

通過(guò)各參數(shù)對(duì)主管管壁彎矩、剪力和主管軸力的影響曲線可以看出，主管管壁彎矩、剪力和主管軸力在負(fù)偏心過(guò)程中存在相互作用的關(guān)系，對(duì)有限元分析結(jié)果進(jìn)行擬合，得到在無(wú)偏心、偏心D／2時(shí)節(jié)點(diǎn)主管軸力與橫向力之間的關(guān)系式和在負(fù)偏心過(guò)程中主管管壁剪力與等效橫向力之間的關(guān)系式，見(jiàn)圖10～圖12。

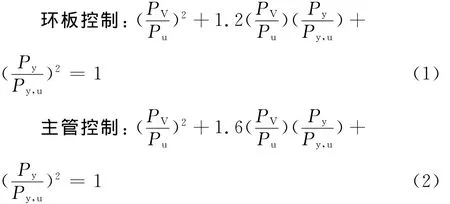
式（1）、（2）是無(wú)偏心時(shí)主管軸力與等效橫向力的關(guān)系式。式中PV為主管軸力；Py為有軸力無(wú)偏心時(shí)節(jié)點(diǎn)的等效橫向力；Pu為有軸力時(shí)節(jié)點(diǎn)的等效橫向力；Pu＝fy·A；fy為主管屈服強(qiáng)度；A為主管截面積；Py，u為無(wú)軸力時(shí)節(jié)點(diǎn)的等效橫向力。

負(fù)偏心距為D／2時(shí)主管軸力與主管管壁剪力之間關(guān)系式：

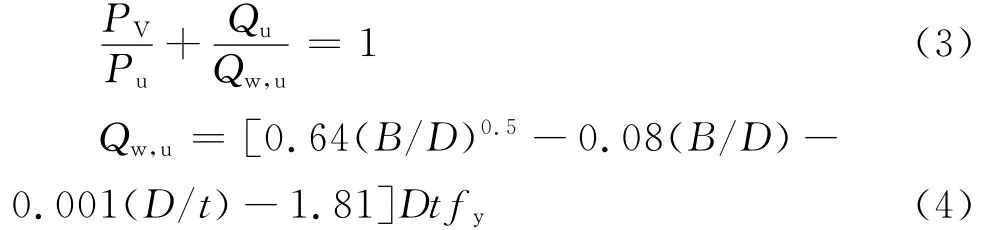
式中：Qw，u為無(wú)軸力時(shí)主管管壁剪力；Qu為有軸力時(shí)主管管壁剪力。

節(jié)點(diǎn)從無(wú)偏心到偏心D／2的過(guò)程中，主管管壁的彎矩和剪力在不斷變化。在主管軸力、主管管壁彎矩和剪力的作用下節(jié)點(diǎn)將發(fā)生局部屈曲。根據(jù)有限元分析結(jié)果進(jìn)行擬合得到節(jié)點(diǎn)等效橫向力與主管管壁剪力之間的關(guān)系曲線見(jiàn)圖12。

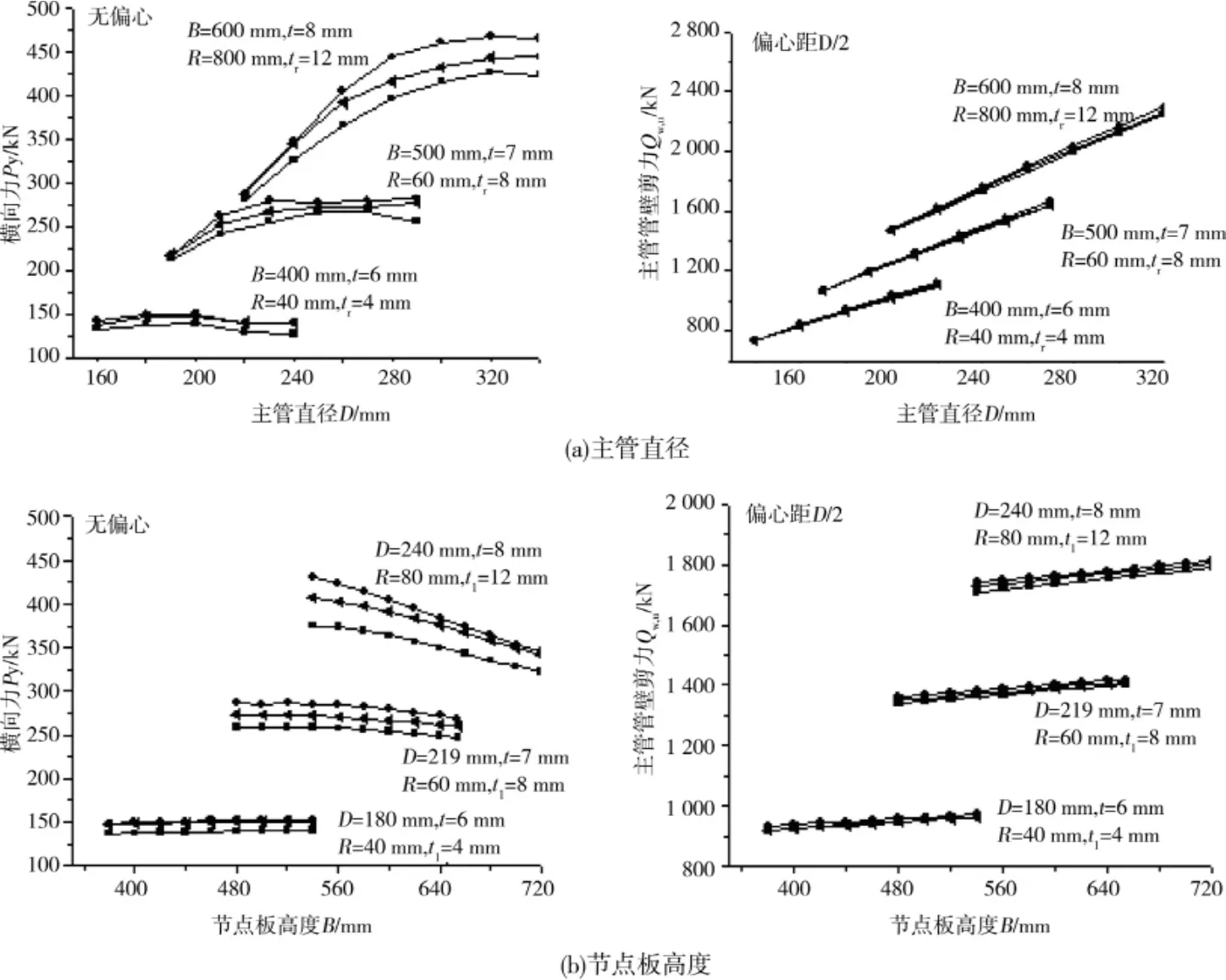
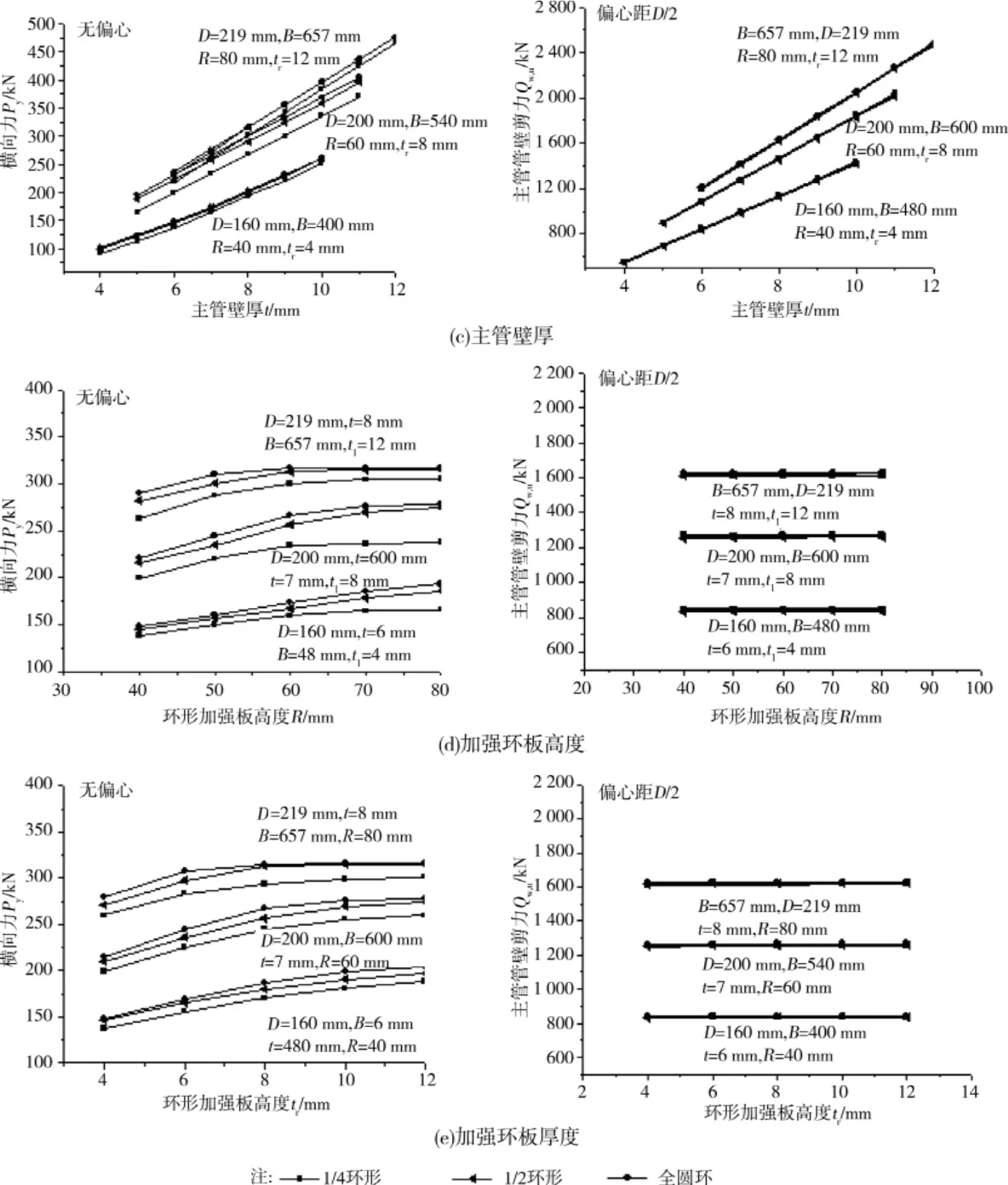
圖9 節(jié)點(diǎn)各參數(shù)對(duì)節(jié)點(diǎn)承載力的影響曲線圖

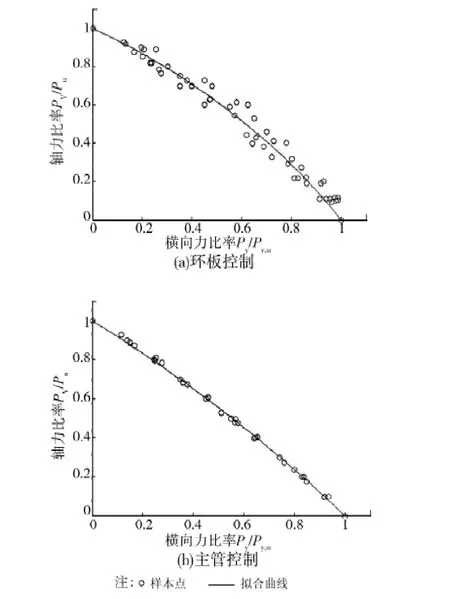
圖10 主管軸力與等效橫向力關(guān)系曲線圖（無(wú)偏心）

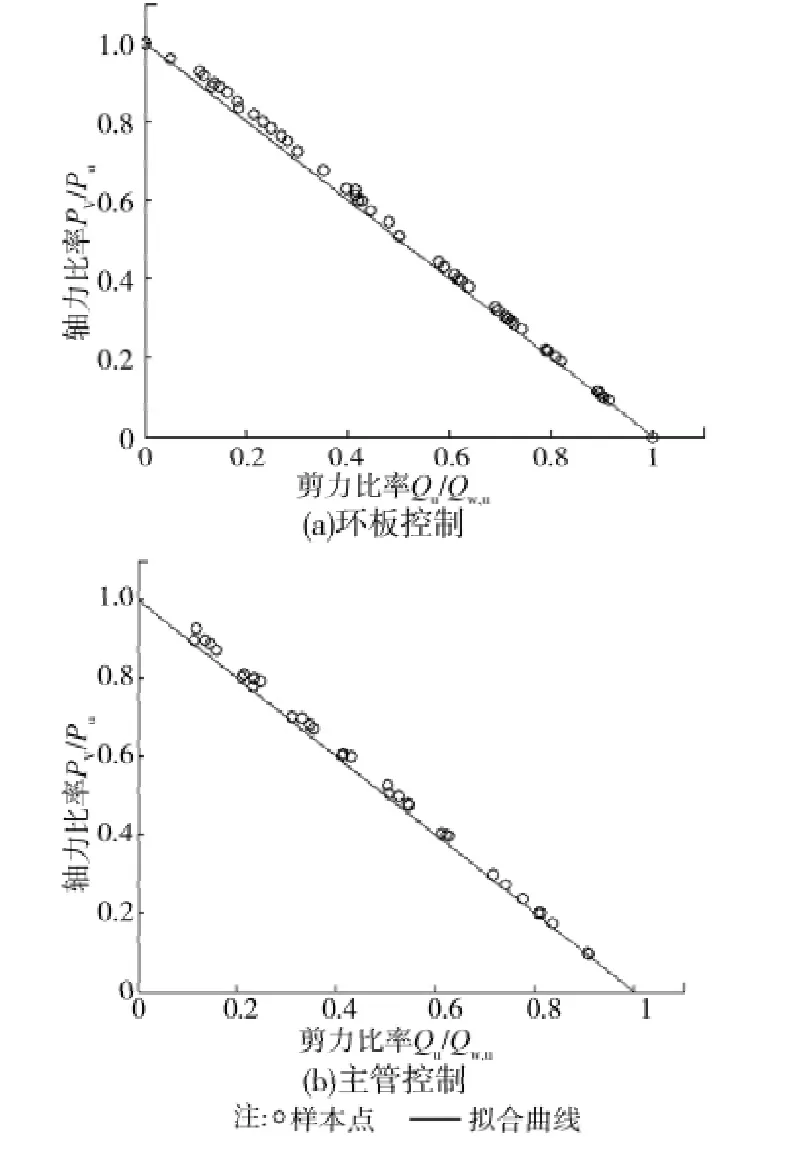
圖11 主管軸力與主管管壁剪力關(guān)系曲線圖（偏心D／2）

環(huán)板控制：

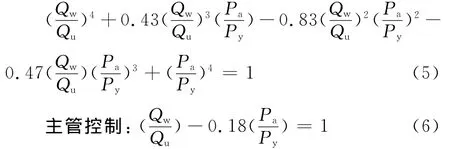
圖12 主管管壁剪力與等效橫向力關(guān)系曲線圖

式（5）、（6）是負(fù)偏心過(guò)程中主管管壁剪力與節(jié)點(diǎn)等效橫向力的關(guān)系式。Pa為有軸力有偏心時(shí)節(jié)點(diǎn)的等效橫向力；Qw為有軸力偏心時(shí)主管管壁剪力。

從式（1）～（6）可以看出：在節(jié)點(diǎn)的幾何尺寸確定的情況下，先要判斷出無(wú)軸力無(wú)偏心時(shí)節(jié)點(diǎn)的承載力是由主管控制還是由環(huán)板控制。在負(fù)偏心距為D／2時(shí)，主管控制和環(huán)板控制的主管管壁剪力與主管軸力的關(guān)系式是相同的。因?yàn)樵谪?fù)偏心距為D／2時(shí)節(jié)點(diǎn)的破壞模式都相同，即節(jié)點(diǎn)下端主管發(fā)生局部屈曲。在負(fù)偏心過(guò)程中，承載力由主管控制和由環(huán)板控制的節(jié)點(diǎn)的主管管壁剪力與等效橫向力的關(guān)系式形式不一樣。承載力由主管控制的節(jié)點(diǎn)主管管壁剪力與等效橫向力的關(guān)系表達(dá)式為線性關(guān)系。在已知主管軸力的情況下，將其值分別代入無(wú)偏心時(shí)節(jié)點(diǎn)等效橫向力與主管軸力的關(guān)系式和偏心D／2時(shí)主管管壁剪力與主管軸力的關(guān)系式中，得到Qu和Mu（Mu＝Py·B）。此時(shí)，根據(jù)彎矩和剪力的關(guān)系式就能得到在不同的偏心距時(shí)的主管管壁彎矩和剪力。反之，知道彎矩，就能求出偏心距，從而算出此時(shí)主管的軸力。3個(gè)等式還可以檢驗(yàn)力的相互組合是否安全，以便用于指導(dǎo)設(shè)計(jì)。

為了驗(yàn)證文中算式的適用性，其計(jì)算結(jié)果與文獻(xiàn)［16］結(jié)果進(jìn)行對(duì)比分析見(jiàn)表4。

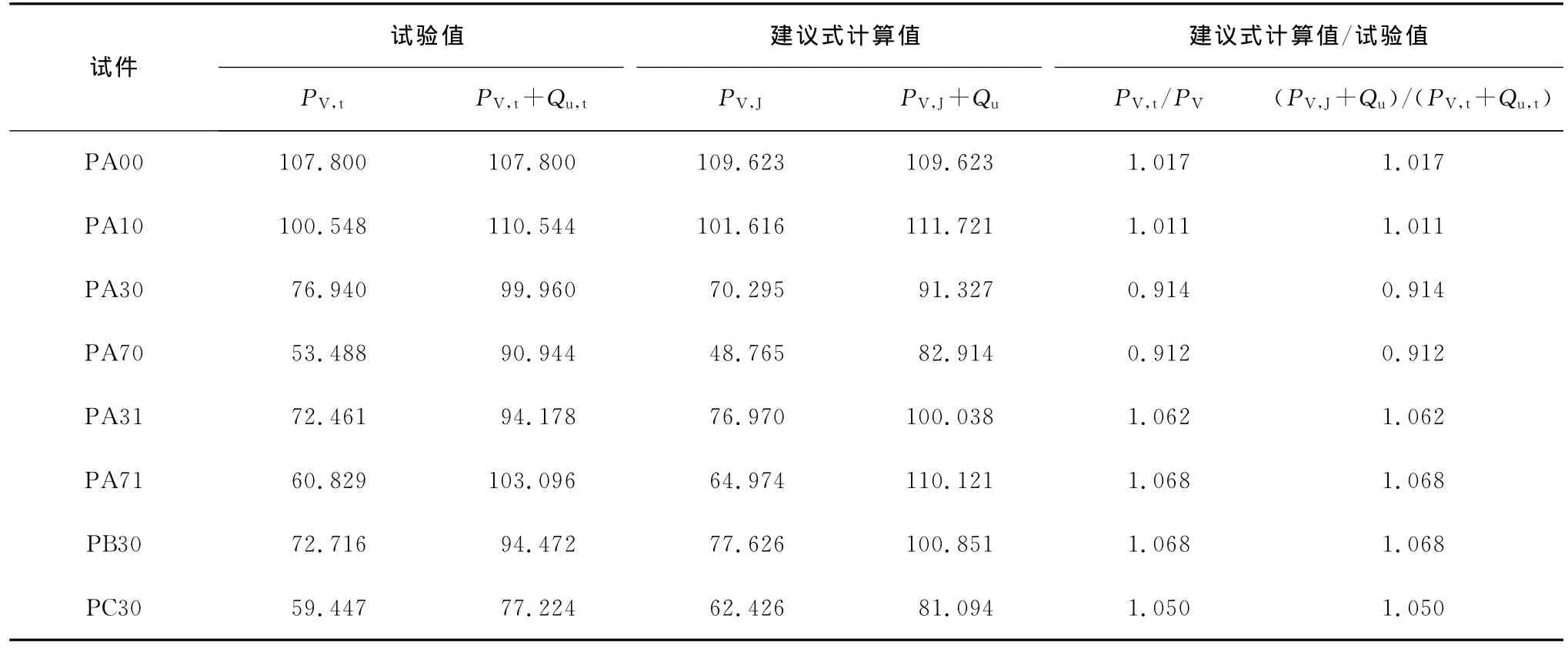
表4 建議式計(jì)算結(jié)果與文獻(xiàn)［16］試驗(yàn)結(jié)果比較

從表4可以看出，建議式計(jì)算值與試驗(yàn)結(jié)果最大相差約9%，吻合較好，建議式具有較好的適用性。

5 結(jié)論

1）根據(jù)等效模型提出的有環(huán)形加強(qiáng)板的鋼管－插板連接K型節(jié)點(diǎn)承載力建議式反映了負(fù)偏心過(guò)程中主管軸力、主管管壁彎矩和剪力之間相互關(guān)系。建議式表面看是反映兩兩之間的相互關(guān)系，實(shí)際上反映了主管軸力、主管管壁彎矩和剪力三者之間的關(guān)系，通過(guò)建議式能估算節(jié)點(diǎn)承載力的上限值。

2）根據(jù)彎矩和剪力關(guān)系式能得到在不同的偏心距的主管管壁彎矩和剪力。反之，知道彎矩，能求出偏心距，從而算出此時(shí)主管的軸力。根據(jù)主管軸力、主管管壁彎矩和剪力三者之間的關(guān)系式可以檢驗(yàn)其相互組合是否安全。

［1］Architectural Institute of Japan.Recommendations for the designed fabrication of tubular structures in steel［S］.Tokyo：Japanese Steel Construct，1990.

［2］The Japanese Steel Tubular Association.Electricity transmitting steel tubular tower manufacture norm［S］.Tokyo：Japanese Steel Construct，1985.

［3］KEPCO.Specification for electric transmission tower design［S］.Tokyo：Japanese Society Steel Construct，1991.

［4］陳以一，趙必大，王偉，等.平面KK型圓鋼管相貫節(jié)點(diǎn)平面外受彎性能研究［J］.土木工程學(xué)報(bào)，2010，43（11）：8－16.

CHEN Yiyi，ZHAO Bida，WANG Wei，et al.Behavior of unstiffened CHS KK－joints under cyclic out－of－plane bending［J］.China Civil Engineering Journal，2010，43（11）：8－16.

［5］孫波，程睿，郭薇，等.空間鋼管－板X(qián)X型節(jié)點(diǎn)靜力性能參數(shù)分析［J］.土木建筑與環(huán)境工程，2010，32（4）：12－18.

SUN Bo，CHENG Rui，GUO Wei，et al.Parametric analysis of the static behavior of gusset plate to CHS XX－joints［J］.Journal of Civil，Architectural ＆Environmental Engineering，2010，32（4）：12－18.

［6］鄭軍.空間X＋雙KK型圓鋼管焊接節(jié)點(diǎn)靜力性能試驗(yàn)研究［J］.太原理工大學(xué)學(xué)報(bào)，2011，42（1）：83－87.

ZHENG Jun.Experimental study on static behavior of space X＋double KK－joints［J］.Journal of Taiyuan University of Technology，2011，42（1）：83－87.

［7］余志祥，閆雁軍，趙世春.K型外套強(qiáng)化矩管桁架節(jié)點(diǎn)滯回性能與恢復(fù)力模型［J］.四川大學(xué)學(xué)報(bào)：工程科學(xué)版，2010，42（6）：66－72.

YU Zhixiang，YAN Yanjun，ZHAO Shichun.The hysteretic behavior and restoring force model of the K－shape outer sleeve RHS joints［J］.Journal of Sichuan University：Engineering Science Edition，2010，42（6）：66－72.

［8］Meng X D，Chen Y Y，Wang W，et al.Experimental research on hysteretic property of unstiffened tubular X－joints under quasi－static out－of－plane bending［C］／／Proceedings of Eleventh East Asia－Pacific Conference on Structural Engineering＆Construction，Taipei，2008：442－443.

［9］Kurobane Y.New developments and pratices in tubular joint design［C］／／International Organizations Institution Welding.Tokyo：Annual Assembly，1981： 197－223.

［10］Wardeneir J.Hollow section joints［M］.Delft：Delft University Press，1982：33－46.

［11］Martinez－Saucedo G，Packer J A，Christopoulos C.Gusset plate connections to circular hollow section braces under inelastic cyclic loading［J］.Journal of Structural Engineering，2008，135（7）：1252－1258.

［12］Willibad S，Packer J A，Voth A P，et al.Throughplate joints to elliptical and circular hollow sections［C］／／11th.International Symposium on Tubular Structures，Quebec，2006.

［13］Ariyoshi M，Makino Y，Choo Y S.Introduction to the database of gusset－plate to CHS tube joints［C］／／Proceedings of 8th International Symposium on Tubular Structures，Singapore：Singapore Steel Construct，1998：22－28.

［14］Kim W B.A study on conections of circular hollow section with gusset plate［J］.J Architectural Inst Korea 1997，13（3）：263－271.

［15］Kim W B.A Study on the local deformation of tubular connection in truss［J］.Conference Korean Society of Steel Construct，1995，7（2）：135－140.

［16］Kim W B.Ultimate strength of tube－gusset plate connections considering eccentricity［J］.Engineering Structures，2001，23（7）：1418－1426.

（編輯 胡英奎）

Effects of Eccentricity on the Ultimate Strength of K－joint with Tube－gusset Plate Connections

WANGWeijia，LIUHongjun，LIZhengliang
（College of Civil Engineering，Chongqing University，Chongqing 400045，P.R.China）

The behavior and strength of tube－gusset connections with tube 219×6 and 1／4 annular ribbed plate subjected to eccentric force is investigated.Non－dimensionalized ultimate strength interaction relations between the wall moment of tube，vertical axial force，and eccentric vertical component force of axial brace force of tube－gusset connections with 1／4（1／2）and annular ribbed plate subjected to eccentric force is researched based on the model of equivalent forces of tubular joint.The parameters which influence the ultimate strength of tube－gusset joint were analyzed and non－dimensionalized ultimate strength interaction－relationships were proposed.It is shown that the proposal formula has theoretical and practical significance for design because of comparation with experimentation.

eccentricity；ultimate strength；tube－gusset connections；the model of equivalent force

TU312.1

A

1674－4764（2012）04－0091－07

2011－11－28

國(guó)家自然科學(xué)基金資助項(xiàng)目（51078367）；中央高校基本科研業(yè)務(wù)費(fèi)資助項(xiàng)目（CDJRC10200016）

王蔚佳（1959－），女，主要從事施工技術(shù)研究，（E－mail）cqdxwwj＠163.com。