基于遺傳優化獲取微陣列最佳分類規則＊

陳湘濤，陳 東

（湖南大學信息科學與工程學院，湖南長沙 410082）

基于遺傳優化獲取微陣列最佳分類規則＊

陳湘濤?，陳 東

（湖南大學信息科學與工程學院，湖南長沙 410082）

基于遺傳編程（GP）提出一種最優規則遺傳算法（BRGA）對分類規則進行優化的方法，獲取最佳分類規則集，此算法可以調整分類器模型的相關參數，在適當增加迭代基礎上大幅提高分類的精確度，具有相當的靈活性和可理解性.利用6個基因數據集檢驗了算法的性能.仿真結果表明，本文提出的算法與其他文獻的方法相比，在具有較高分類精確度和穩定性前提下大幅降低了計算復雜度及冗余.

最優規則遺傳算法；微陣列；遺傳編程；分類規則；計算復雜度

生物醫學研究表明，人類大多數疾病的發病機制，比如癌癥，從根本上來說都和基因息息相關.微陣列數據是將樣本實驗形成的影像轉為基因表達矩陣，矩陣行表示基因，列表示類別樣本，矩陣中的元素描述不同基因在不同樣本的表達水平.

由于微陣列芯片技術［1］獲得的基因數據數量遠大于樣本數量，隨著維數的增加，最大的障礙則是在高維特征空間運算時存在的“維數災難”.微陣列大量基因數據僅為樣本分類提供了少數有分類意義的、具有明顯特征的基因.因此，在樣本分類之前，選擇特征基因是至關重要的，這直接影響到之后生成的分類器性能.微陣列分類作為生物指標的探索成為生物信息學一個重要的課題，事實上，由于存在更多的癌癥類型和潛在的癌癥子類，如果展開腫瘤分類問題到多重腫瘤類別，數據集包含更多的類別和非常少量的樣本，問題將變得更具有挑戰性.

一些研究報告指出，在基因選擇部分使用遺傳算法能改進微陣列數據的分類性能［1－2］，因此，遺傳算法已廣泛用于解決包括數據分類的各種難題［3－4］.本文提出一種最優規則遺傳算法（Best Rule Genetic Algorithm，BRGA），選用一種基于遺傳優化的分類算法生成分類規則，用二進制向量表示分類規則，初始化規則集，設定相應的適應度及初始種群的規模，通過變異產生一定數量的最優分類規則.通過實驗，使用6個基因表達數據集來驗證算法的性能.

微陣列數據分類技術通常包含2部分內容：1）基因選擇；2）構建分類器模型.文獻［5］在基因選擇部分使用排列值計分RBS算法，很好地解釋了基因之間的相關性，大幅降低基因矩陣維度，在一定程度上減少了計算復雜性；在構建分類器部分提出了LCR方法，可以用很少的基因構造形成分類規則，提高了算法的可理解性.但分類規則的形成過程仍存在很多不足，如分類器模型中規則形成框架過于縝密，容易導致過擬合，產生龐大規則集的迭代過程相當繁瑣，并產生大量冗余的規則，導致計算復雜度較高且算法收斂速度較低.分類器的構建則是整個技術的核心所在，傳統的微陣列分類方法有：加權投票（WV）［6］，K近鄰（k-NN）［7］，支持向量機（SVM）［8］，費舍爾線性判別分析（LDA）［9］，人工神經網絡（ANN）［10］，遺傳規劃（GP）［11］，最小二乘邏輯回歸［12］和樸素貝葉斯方法［13］等.由于它們僅僅聚焦于分類性能，而不能進一步提供任何醫學和生物學依據，導致這些分類算法往往產生僵硬的分類系統，存在穩定性弱和開銷大的特征，缺乏可擴展性.決策樹算法［14］和隨機森林算法［15］基于決策規則產生分類器模型，此類算法獲得的分類規則在某種意義上包含了生物體基因之間的相關性，但如果訓練樣本存在小的差異會導致決策樹結構產生大的變化，致使分類器缺乏穩定性，這些分類方法仍然存在很大的局限性.

1 BRGA方法的基本思想

BRGA算法是在遺傳優化的基礎上，將分類規則集作為種群，使用二進制串表示其中任意一條分類規則，計算對應于基因屬性的比較關系的分類規則適應度值，經過若干代的繁殖過程，包括選擇、交叉和變異運算，反復迭代優化，獲取具有較高適應度的最佳分類規則.

1.1 基因選擇

本文用BRS方法［5］對微陣列數據集按排列值打分排序，分別選擇分值最高的c／2和最低的c／2個（c為偶數）有重大表達意義的基因.

1.2 分類規則形成

首先將基因選擇部分產生的c個基因的排列值矩陣R按行建立比較關系，規則表示為［b1b2…bc］且b1，b2，…，bc∈｛0，1｝，如果比較關系中包含矩陣J中第i行基因排列值，則bi∈｛b1，b2，…，bc｝為1，反之bi為0.然后獲取滿足規則關系的癌樣本和正常樣本的數量，分別計算其對應類別樣本總數的比值Ct和Cn，二者之差的絕對值作為適應度F，如果Ct大于Cn，表示該規則為癌類別，用1表示；相反，該規則為正常類別，用0表示.利用BRGA算法優化初始規則集，從而獲取最佳分類規則集.

設Ft為適應度閾值，適應度f大于Ft的規則為最優規則；Nt為最優規則數量閾值，最優規則集規則數m達到值Nt則收斂；K為規則種群繁殖的代數，每經過K代則將適應度閾值Ft下調一個合適的值F＿ad，以防止算法無法收斂.

1.3 分類預測

最佳分類規則集用來預測測試樣本的類別，計算測試樣本對應規則中基因的排列值，判斷規則集中每條分類規則是否滿足測試樣本，依次將測試樣本歸類，如果滿足癌樣本分類規則，將其歸為癌類別1，如果不滿足癌樣本分類規則，則歸為正常類別0，反之亦然.采用MV［5］（Majority Voting）方法累計不同類別的規則適應度值，如果某類的適應度值總和大于另一類適應度值總和，那么最終預測測試樣本屬于該類別.

2 BRGA算法優化過程

將微陣列基因數據訓練樣本的基因表達值矩陣轉換為其相應的排列值矩陣形式，用BRS方法打分，再排序，取分值最高和最低的能表達樣本特征的少量基因.然后用BRGA算法產生符合特征基因排列值對應不相同類別的樣本大小關系的規則，其中，符合某一樣本類別不同基因排列值大小關系的規則應盡量不符合另一樣本類別的相應基因排列值的大小關系，找出所有這樣的規則，再用這些規則生成分類器對未知樣本進行分類預測.

2.1 規則的形式

在少量特征基因的排列值矩陣形成的基礎上，根據矩陣的維度M確定二進制規則的位數為M，R1，R2，…，RM對應排列值矩陣從上至下相應的行（1，2，…，M），規則中1表示矩陣對應二進制規則相應位置的行與其他行存在比較關系，0則表示在此規則中該行不存在比較關系.

例如，規則的位數固定為M位，矩陣排列值行比較關系R1＜R2＜R5；M＝10，那么此關系可表示為［1 1 0 0 1 0 0 0 0 0］，比較關系方向統一為大于或小于符號，R1，R2，R5表示每一樣本在第1，2，5個基因位置相應的排列值.

2.2 規則的生成

BRGA方法基于遺傳算法優化分類規則，將具有高適應度的分類規則歸并至最佳分類規則集，最終達到最優的樣本預測性能，極大地提高了算法的收斂性，BRGA算法偽代碼示意圖如圖1所示.BRGA算法的步驟為：

1）初始化規則集.生成初始規則種群為M＊N階全零矩陣形式Popus，其中每一條規則rule（i）是位數為N，且值全為零的一維數組，且i∈｛1，2，…，M｝，設定合適的適應度閾值Ft，最佳規則集規則數閾值Nt及K代調整系數F＿ad.

2）變異運算.變異運算aberrance（popus）是隨機改變種群規則中某一位置的值，通過對父代規則集變異形成子代規則集，由于微陣列數據的特征基因排列值在不同樣本中差異較大，規則適應度值隨比較關系所包含基因數增加基本呈遞減趨勢，因此，BRGA算法在變異運算中設置了限制規則中1的數量（即比較關系的基因數）閾值Lt，如果超過Lt將規則位全部清零，從而降低冗余規則的產生，并能有較防止過擬合，提高了分類性能.

3）計算規則適應度.函數Fit（）計算Popus規則種群中每一條規則對應的適應度F，輸出對應的規則rule及類別標簽label.

圖1 BRGA算法偽代碼示意圖Fig.1 BRGA pseudo-code schematic diagram

假設任一規則的適應度為F，如果滿足該規則的某類樣本的數量為a，另一類樣本的數量為b，那么，該規則相應的適應度為F＝｜a－b｜.很容易看出F值越大，則越能體現不同樣本的差異.

那么，規則預測類別標簽label可以表示為：如果a＞b，樣本為A類，比如癌癥樣本，則label＝1；如果a＜b，樣本為B類，如正常樣本，則label＝0.

4）獲取最佳規則.計算子代規則集的規則適應度F，如果F｛F1，F2，…，Fn｝中存在大于等于Ft的值，則將其對應的規則、適應度值及預測類別標簽label保存至最佳規則集，去掉相同的規則，每隔K代，適應度閾值Ft向下調整幅度值F＿ad，確保算法收斂，并判斷規則數量是否等于Nt，如果相等則結束，否則重復步驟2）－4）.

3 實驗結果與分析

本文實驗使用了公開的6個基因表達數據集，分別為前列腺癌［16］，結腸癌［17］，白血病［18］，淋巴瘤［19］，肺癌［20］和腦癌［21］，這些數據集為二類和多類基因表達譜.仿真實驗所使用的軟件系統為MATLAB7.0，硬件環境為主頻2 GHz的Intel雙核微處理器、內存為2 GB的PC機.使用結腸癌數據集闡述BRGA算法實施過程，該數據集包含62個樣本，2 000個基因表達水平，樣本由40個腫瘤和22個正常樣本組成.結腸癌基因表達值如表1所示.

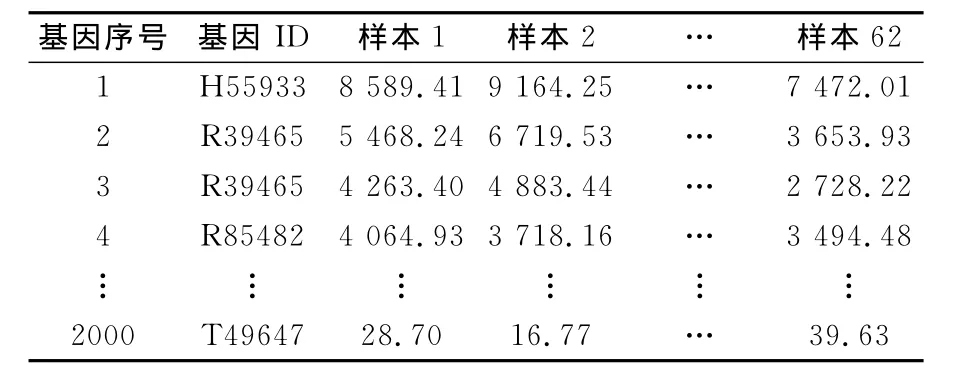
表1 結腸癌基因表達值Tab.1 Colon cancer gene expression values

在基因選擇部分利用文獻［5］使用的RBS方法將每個樣本的每一基因表達值轉換成相應的排列值（見表2）.

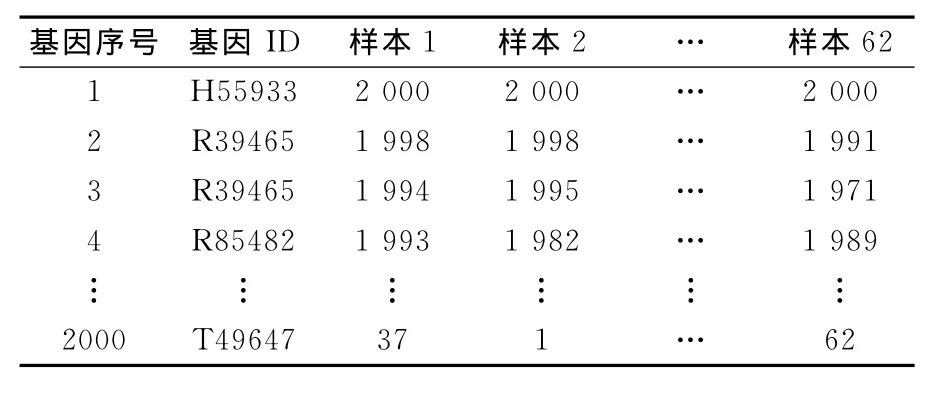
表2 結腸癌基因排列值Tab.2 Colon cancer gene rank values

從分類性能和運算耗時多方面因素綜合考慮，在本實驗中選擇RBS分值最高和最低的具有重大表達意義的屬性基因各10個（共計20個基因），作為形成分類規則的基礎，如表3所示.

使用本文第2節提到的方法來初始化規則集，選擇合適的適應度閾值Ft∈（0，1］及規則數閾值Nt，同時設定規則中比較關系所包含的基因數量Lt，通過對結腸癌數據集選擇的上述20個重要的基因實施該方法，可獲得一個具有一定數量Nt的最優預測規則數據集（包含類標簽為1的癌癥類標簽，為0的正常類標簽以及適應度值F），且每一規則適應度值均大于或等于Ft，同時，設定每隔K代Ft調整值F＿ad，確保算法收斂于最優規則集.

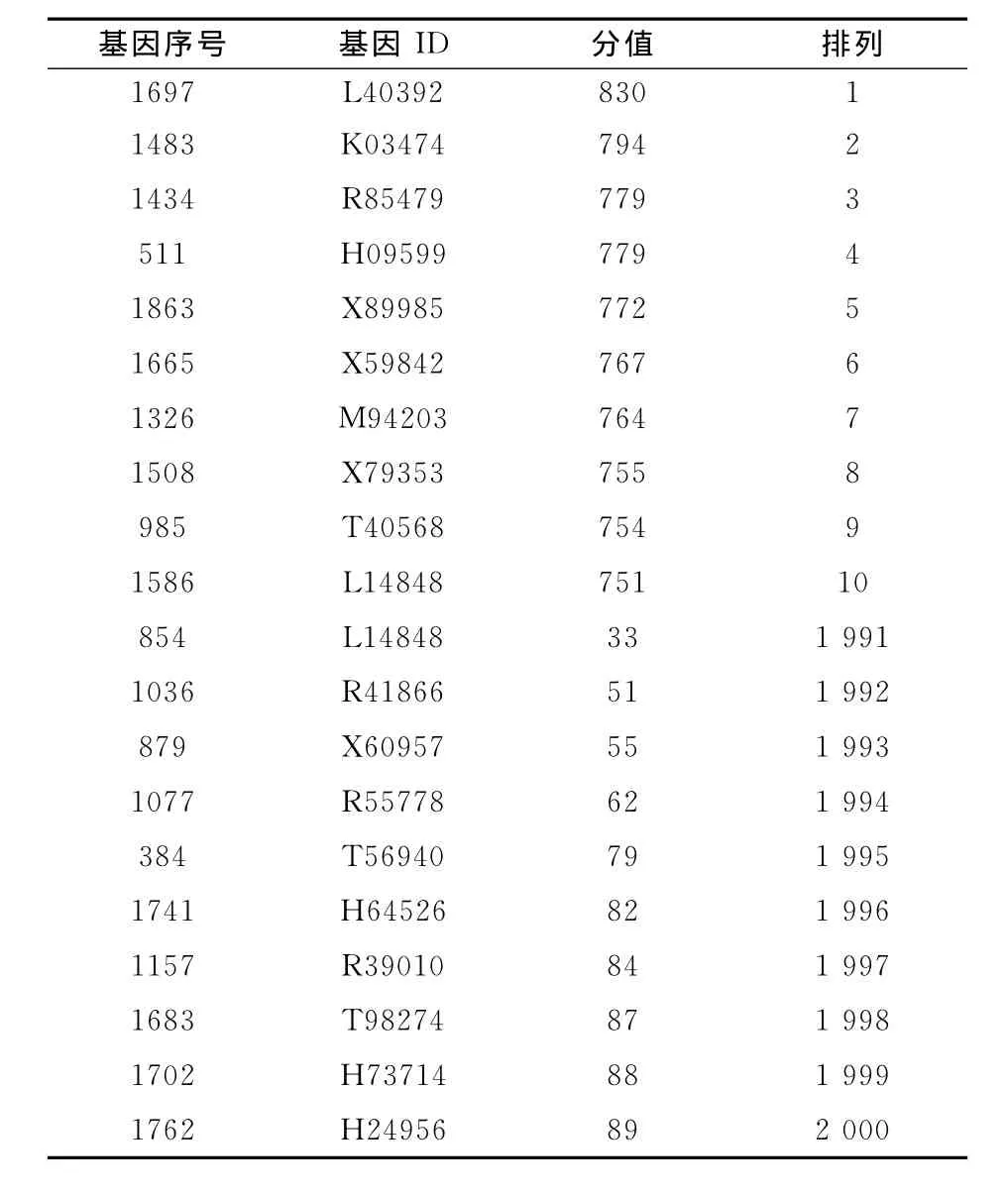
表3 20個結腸癌重要基因Tab.3 Twenty significant Colon cancer genes

用留一交叉校驗法（Leave-One-Out Cross Validation，LOOCV）驗證規則集對結腸癌數據集分類的性能，將62個樣本分為訓練集和測試集，包含61個訓練樣本和單個測試樣本，此過程重復62次.對樣本集中每個樣本分別作一次預測，以此來檢驗算法的準確性.最后用規則集對每個樣本分別累計其滿足癌癥類規則適應度與正常類規則適應度之和，兩者相減，如果癌癥類規則適應度大于正常規則適應度，則預測此樣本屬于癌癥樣本，反之為正常樣本.表4為使用4條規則的最優規則集預測結腸癌測試樣本的類別.

用同樣的方法對另外3個兩類數據集進行分類預測，得到LOOCV精確度與運算時間與文獻［5］比較結果（見表5）.

采用BRGA算法用于多類（n類）數據集分類時，先將正常樣本和癌樣本分為2大類，再依次把訓練集中癌樣本（n－1子類）的每一子類和剩余其他子類（n－2子類）的樣本分為兩類，用BRGA算法優化規則獲得n個最佳分類規則集，即把多類問題轉化為n個兩類問題，再對n個兩類最佳規則集的預測精確度求平均值，得到最終的分類性能.將BRGA算法和幾種相關文獻中提及的分類方法在性能上進行比較，結果如表6所示.

表4 結腸癌樣本預測Tab.4 Colon cancer sample prediction

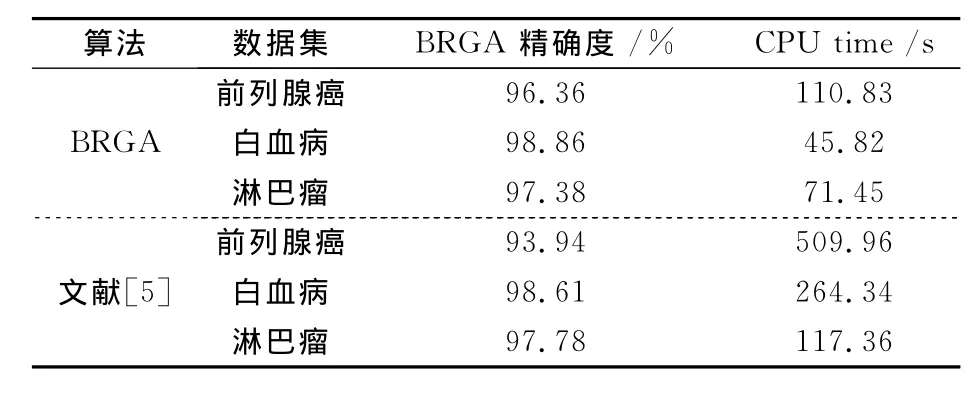
表5 算法性能及運算耗時比較Tab.5 Performance and elapsed time comparison

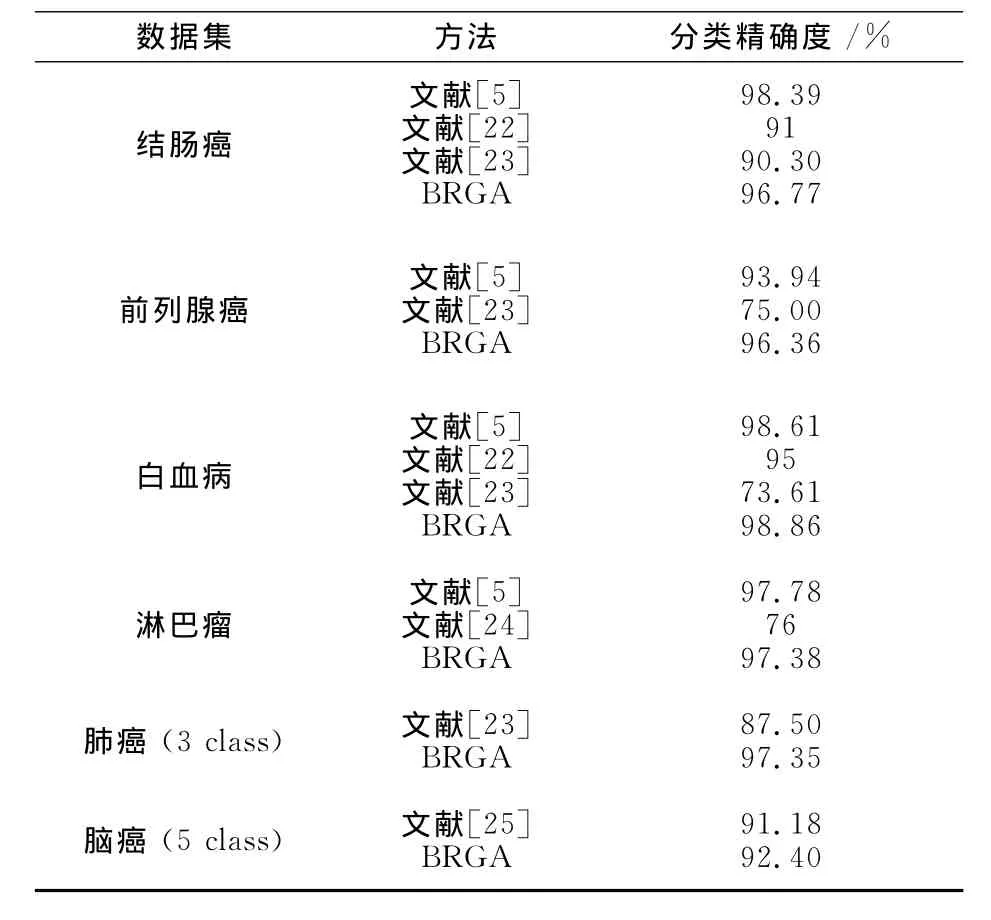
表6 算法性能比較Tab.6 Performance comparison

由表5和表6可以發現，本文提出的算法與其他文獻中的算法比較具有較高的分類性能，且本文算法能快速地從復雜基因排列中提取最優的分類規則，極大地降低了計算復雜度及運算時間；算法簡單易理解，穩定性高，對腫瘤和正常基因的分類及疾病的不同子類的劃分都具有優良的性能.

圖2為BRGA算法在6個不同數據集對應不同最優規則數量閾值Nt的分類預測性能分布圖.由圖1可知，當Nt值為5～10時，大部分數據集均能較好地收斂于最佳分類規則集，達到相對理想的分類性能；BRGA算法在二類和多類微陣列基因數據集的分類性能均能在合適的Nt值情形下達到高分類精確度，降低了冗余規則在分類規則中出現的概率，并具有較高的收斂性和較強的泛化能力.

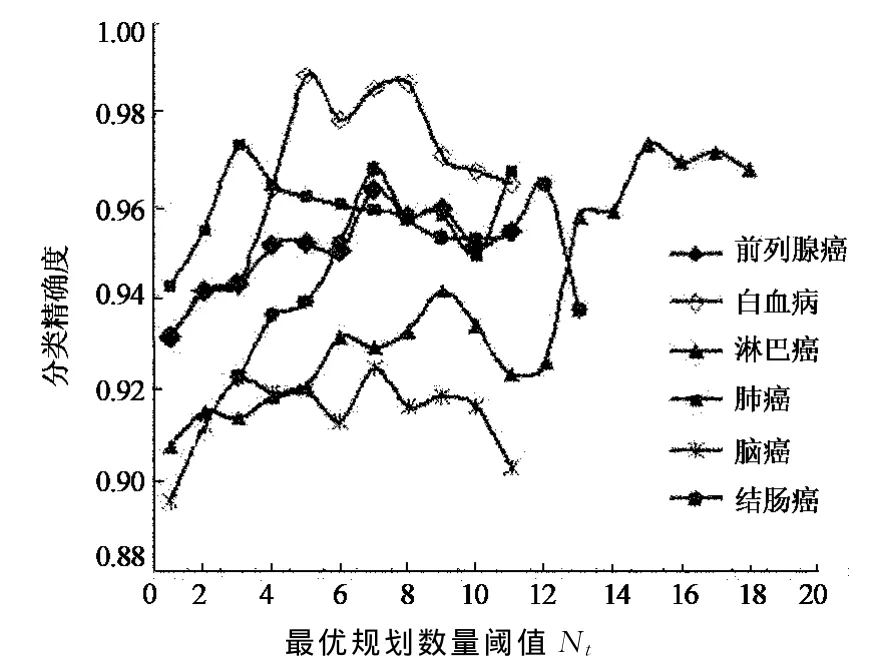
圖2 BRGA性能分布圖Fig.2 BRGA performance distribution map

4 結 論

本文提出的BRGA算法很好地解決了用微陣列基因表達值構建分類決策規則普遍速度慢的難題，通過調整適合規則的適應度值及相關參數對初始規則集進行優化，該算法能很快收斂于最優分類規則集.采用6個數據集驗證了該算法的性能，實驗結果表明，BRGA算法具有較高的精確度和極少的分類運算耗時（CPU time）.當然，由于實驗條件和生物學發展的局限性，該算法有待進一步提高和完善.

［1］ HENGPRAPROHM S，MUKVIBOONCHAI S，THAMMASANG R，etal.A GA-based classifier for microarray data classification［C］／／Proceedings of 2010 International Conference on Intelligent Computing and Cognitive Informatics（ICICCI 2010）.Kuala Lumpur：IEEE Computer Society，2010：199－202.

［2］ OOI C H，TAN P.Genetic algorithms applied to multi-class prediction for the analysis of gene expression data［J］.Bioinformatics，2003，19（1）：37－44.

［3］ BANDYOPADHYAY S，MURTHY C A，PAL S K.Pattern classification with genetic algorithms［J］.Pattern Recognition Letters，1995，16（8）：801－808.

［4］ BANDYOPADHYAY S，MURTHY C A，PAL S K.VGA-classifier：design and applications［J］.IEEE Transactions on Systems，Man and Cybernetics-Part B，Cybernetics，2000，30（6）：890－895.

［5］ GANESH-KUMAR P，AMMU V，VICTOIRE T A A.Building decision rules using a novel data driven method for microarray data classification［C］／／2011 International Conference on Process Automation，Control and Computing（PACC 2011）.Coimbatore：IEEE Express Conference Publishing，2011：1－6.

［6］ GOLUB T R，SLONIM D K，TAMAYO P，et al.Molecular classification of cancer：class discovery and class prediction by gene expression monitoring［J］.Science，1999，286（5439）：531－537.

［7］ WU Wei，XING E P，MYERS C，et al.Evaluation of normalization methods for cDNA microarray data by k-NN classification［J］.BMC Bioinformatics，2005，6：191－211.

［8］ YOONKYUNG L，CHEOL-KOO L.Classification of multiple cancer types by multicategory support vector machines using gene expression data［J］.Bioinformatics，2003，19（9）：1132－1139.

［9］ JAEWON L，JUNGBOK L，MIRA P，et al.An extensive comparison of recent classification tools applied to microarray data［J］.Computational Statistics ＆Data Analysis，2005，48（4）：869－885.

［10］KHAN J，JUN S，RINGNER M，et al.Classification and diagnostic prediction of cancers using gene expression profiling and artificial neural networks［J］.Nat Med，2001，7（6）：673－679.

［11］HONG J H，CHO S B.The classification of cancer based on DNA microarray data that uses diverse ensemble genetic programming［J］.Artificial Intelligence in Medicine，2006，36（1）：43－58.

［12］TANG E K，SUGANTHAN P N，YAO X.Gene selection algorithms for microarray data based on least square support vector machine［J］.BMC Bioinf，2006，7：95－110.

［13］JOHNSON W E，LI C，RABINOVIC A.Adjusting batch effects in microarray expression data using empirical bayes methods［J］.Biostatistics，2007，8（1）：118－127.

［14］YU WANG，IGOR V T，MARK A H，et al.Gene selection from microarray data for cancer classification—a machine learning approach［J］.Computational Biology and Chemistry，2005，29（1）：37－46.

［15］RAMON D U，SARA A A.Gene selection and classification of microarray data using random forest［J］.BMC Bioinformatics，2006，7：3.

［16］WELSH J B，SAPINOSO L M，SU A I，et al.Analysis of gene expression identifies candidate markers and pharmacological targets in prostate cancer［J］.Cancer Res，2001，61：5974－5978.

［17］ALON U，BARKAI N，NOTTERMAN D A，et al.Broad patterns of gene expression revealed by clustering analysis of tumor and normal colon tissues probed by oligonucleotide arrays［J］.PNAS，1999，96（12）：6745－6750.

［18］Broad Institute.Cancer program data sets［EB／OL］.［2012－01－01］.http：／／www.broadinstitute.org／cgi-bin／cancer／datasets.cgi.

［19］ASH A A，MICHAEL B E，ERIC R D，et al.Distinct types of diffuse large B-cell lymphoma identified by gene expression profiling［J］.Nature，2000，403（4）：503－511.

［20］BHATTACHARJEE A，RICHARDS W，STAUNTON J，et al.Classification of human lung carcinomas by mRNA expression profiling reveals distinct adenocarcinoma subclasses［J］.PNAS，2001，98（24）：13790－13795.

［21］SCOTT L P，PABLO T，MICHELLE G，et al.Gene expression－based classification and outcome prediction of central nervous system embryonal tumors［EB／OL］.［2012－01－01］.http：／／www.broadinstitute.org／mpr／CNS／.

［22］SHI Chao，CHEN Li-hui.Feature dimension reduction for microarray data analysis using locally linear embedding［C］／／Proceedings of 3rd Asia-Pacific Bioinformatics Conference（APBC 2005）.Singapore：Imperial College Press，2005：211－217.

［23］TAN A，NAIMAN D，XU L，et al.Simple decision rules for classifying human cancers from gene expression profiles［J］.Bioinformatics，2005，21（20）：3896－3904.

［24］FUREY T S，CRISTIANINI N，DUFFY N，et al.Support vector machine classification and validation of cancer tissue samples using microarray data［J］.Bioinformatics，2000，16（10）：906－914.

［25］JUNBAI W，TROND H B，INGE J，et al.Tumor classification and marker gene prediction by feature selection and fuzzy c-means clustering using microarray data［J］.BMC Bioinformatics，2003，4：60－71.

Obtaining Optimal Microarray Data Classification Rule by GA-based Optimizing

CHEN Xiang-tao?，CHEN Dong
（College of Information Science and Engineering，Hunan Univ，Changsha，Hunan 410082，China）

Based on Genetic Programming（GP），this paper proposed an approach called Best Rule Genetic Algorithm（BRGA）for optimizing classification rule，and gained the best classification rule set.This algorithm can adjust relevant parameters of classifier model，substantially improve the performance of classification by increasing appropriate iteration，therefore it has considerable flexibility and intelligibility.The performance of the proposed approach was evaluated by using six gene expression data sets through simulation.From the result，it is found that the proposed approach reduces computational complexity and redundancy with good classification accuracy and stability than approaches reported in other literatures so far.

Best Rule Genetic Algorithm（BRGA）；microarrays；Genetic Programming（GP）；classification rule；computational complexity

TP391

A

1674-2974（2012）08-0081-06＊

2011-12-19

國家林業公益性行業科研專項經費資助項目（201104090）

陳湘濤（1973—），男，湖南新寧人，湖南大學副教授，博士

?通訊聯系人，E-mail：xtchen2009＠163.com