非獨立情況下二維隨機變量特征函數性質的推廣與應用

吳雄韜，胡伯霞

（衡陽師范學院 數學與計算科學系，湖南 衡陽 421002）

0 引 言

特征函數是處理概率問題的有用工具，對隨機變量序列的收斂問題起到很重要的作用，可以把隨機變量序列的收斂問題轉化為一般函數的序列的收斂問題來進行處理。獨立情況下特征函數有很多的性質，如文獻［1］－［2］，特別是特征函數與隨機變量的k階矩之間的性質對于轉化矩的計算有重要的現實意義，同時也有很多學者對獨立情況下多維隨機變量的特征函數的性質進行了研究如文獻［3］－［5］而對于非獨立情況，相應的結論幾乎沒有，本文在非獨立情況下推廣了特征函數的二階導數與二階矩及協方差之間的一些聯系，并利用二維正態分布的特征函數對推廣的性質進行了具體應用和檢驗。

設（X1，X2）是一個二維隨機變量，為了討論需要引入如下記號：

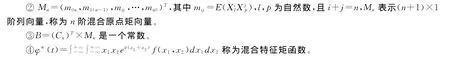
1 非獨立情況下二維隨機變量特征函數的性質

性質1.1 設（X1，X2）是一個二維隨機變量，若X1＋X2的特征函數φ（t）具有n階連續導數，且X1與X2的n階混合原點矩存在，則有φ（k）（0）＝B×ik（k＝1，2，…，n）。

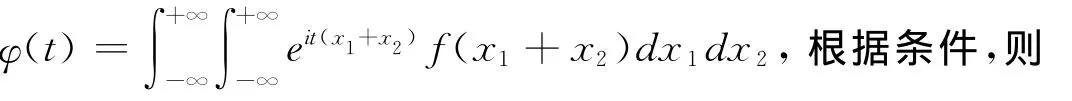
性質2 設φX1（t），φX2（t），φX1＋X2（t）分別是X1，X2，X＋X2的特征函數，且都二階可導，φ＊（x）為X1X2的特征函數，則有2φ＊（t）＝φ″X1（t）＋φ″X2（t）－φ″X1＋X2（t）.

證明： 設（X1，X2）為二維連續型隨機變量，其聯合密度函數為f（x1，x2），離散情況可以類似處理，由于φX1（t），φX2（t），φX1＋X2（t）二階可導，則有

2 非獨立情況下二維隨機變量特征函數的性質

性質1.2正確性得到驗證。

［1］孫榮恒.應用概率論［M］.北京：科學出版社，2006.

［2］金冶明，李永樂.概率論與數理統計［M］.長沙：國防科技大學出版社，1997.

［3］邱德華，文林.特征函數的性質［J］.大學數學，2008，24（6）：187－192.

［4］徐玉華.關于概率論中特征函數性質的幾點討論［J］.荊州師范學院學報，2003，26（2）：17－19.

［5］程偉.Banach空間中廣義特征函數的性質及其應用［J］.天津商學院學報，2006，26（6）：48－50.