類別變量的結構方程模型及其應用*

王 歡 韓 海 蔡紹暉 梁 巧 吳肖蒙 王波棟 張志敏 柳士順

與建立在連續變量基礎之上的結構方程模型不同，類別變量的結構方程模型(structural equation model with categorical observed variables)中均值、方差和協方差變得沒有意義。如果仍然運用以積差相關系數矩陣為基礎的分析方法，就會導致不正確的結果和無效的結論，因此，對類別變量的結構方程模型的分析需要完全不同的統計技術來完成。

類別變量結構方程模型的分析方法

結構方程模型又稱為協方差結構分析(covariance structure analysis)，其基本思想就是用樣本的方差－協方差矩陣(以下簡稱協方差矩陣)去擬合根據研究假設推導出的協方差矩陣。可見，協方差矩陣是結構方程模型的分析基礎。類別變量結構方程模型是基于多項相關系數的協方差矩陣。模型的參數估計方法使用加權最小二乘法〔1〕。

1.多項相關系數與漸近協方差矩陣

任何類別都有一個分類原則，在進行類別變量的結構方程模型分析時，類別變量的分類假設如下:

如果類別變量 x包含 k類，分別記為:1，2，．．．k，假設存在一個作為分類基準的潛在連續變量x*則有:

其中 i=1，2，…k;

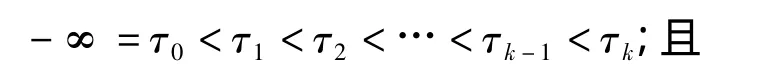
同樣地，對于類別變量y來講，也做類似的假設，即以潛在連續變量y*作為分類基準。為方便起見，假設x*與y*服從二元正態分布，則可通過極大似然估計法，估計出x*與y*的積差相關系數，此種相關系數就是多項相關系數(polychoric correlation);當x與y均為二分變量時，此種相關系數就是四項相關系數(tetrachoric correlation)。以多項相關系數為基礎估計出的多個類別變量的協方差矩陣就是估計的漸進協方差矩陣(estimated asymptotic covariance matrix)，即類別變量結構方程模型的分析矩陣。

2.模型的參數估計

結構方程模型的分析原理主要是通過協方差矩陣的分析導出選定的參數，并對模型的擬合情況進行評價。由于校正加權矩陣(correct weight matrix)可以成為漸進協方差矩陣的一致估計，因此，對基于漸進協方差矩陣的結構方程進行分析時，采用的是加權最小二乘法(weighted least squares)〔2〕。加權最小二乘法要求樣本量要大，缺失值要少。

應用實例

焦慮和抑郁是兩種常見的精神障礙，對個人和社會帶來了負擔，是現代社會不可忽視的健康問題〔3〕。目前，對生活方式與抑郁和焦慮之間關系的研究還比較少〔4〕，日本學者以中老年為對象探討了生活方式對抑郁的預測作用〔5〕。本研究以廣東、上海、河南、浙江等省市機關和企事業單位的在職人員為對象，采用問卷調查法，發放問卷600份，回收有效問卷452份。其中，男性占64.8%;25歲以下的占17.7%，26歲至35歲占52.6%，36至45占24.2%，45歲以上占5.5%;研究生及以上學歷的占4.7%，本科占26.4%，大專占31.3%，大專以下占10.6%。生活方式的測量工具是由Belloc和 Breslow開發，經Morimoto等人修訂的包含八個項目的量表〔6－8〕;對抑郁與焦慮的測評使用的是Lowe等人所提煉的自陳式量表〔3〕;具體內容見表1。問卷的引導語為“根據近四個星期的情況，針對下列描述，選擇最能反映您實際狀況的答案”。LS3、LS6、DEP1、DEP2、ANX1 和 ANX2 為反向記分，其他各項目均按各自的等級從高到低記分。例如:“是否吃早餐”的記分為:0－1－2;“鍛煉身體”的記分為:1－0;“無節制地飲酒”的記分為:2－1－0。

表1 生活方式與抑郁和焦慮的測評量表

數據處理方法與分析結果

本研究選用Lisrel 8.7對所取得的數據進行了處理分析。首先，讀取數據，進入“PRELIS”界面，按照“Data－Define Variables”定義變量，通過“Statistics－Output Options－Moment Matrix;Asymptotic Covariance Matrix”可得到各個變量的臨界值、相關系數矩陣和漸近協方差矩陣及其檢驗結果。本研究的卡方檢驗和接近擬合(close fit)均達到良好水平。

接著，對假設模型進行檢驗，檢驗程序如下:

HEALTH ANANYSIS

Observed Variables:

LS1 LS2 LS3 LS4 S5 LS6 LS7 LS8 DEP1 DEP2 ANX1 ANX2

correlation matrix from file LS.pom

asymptotic covariance matrix from file LS.acc

sample size:452

latent variables:Lstyle DEP ANX

relationshios:

LS1=1#LStyle

LS2－LS8=LStyle

DEP1=1#DEP

DEP2=DEP

ANX1=1#ANX

ANX2=ANX

DEP=LStyle

ANX=LStyle

lisrel output:nd=3 sc me=wls

path diagram

end of problem

根據 J?reskog ＆ S?rbom〔9〕的建議，本研究報告了一些主要的擬合指數，具體指標見表2。各項擬合指數均達到理想水平，假設模型得到驗證。

生活方式與抑郁和焦慮之間關系的完全標準化解見圖1，圖中各個參數的t檢驗均達到0.01的顯著水平。生活方式量表中的八個項目一致地聚合為一個潛在變量，即生活方式;并且與抑郁和焦慮呈負相關關系。也就是說，生活方式越健康，患抑郁癥和焦慮癥的幾率就越低;生活方式越不健康，抑郁和焦慮的程度就越高。

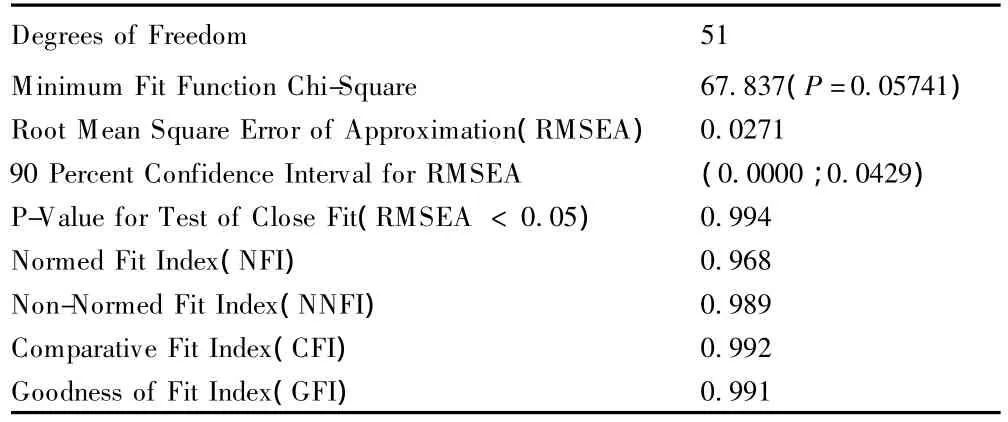
表2 假設模型的主要擬合指標(N=452)

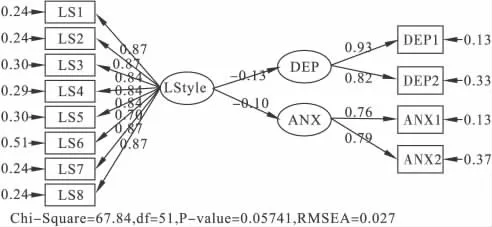
圖1 生活方式與抑郁和焦慮之間關系的路徑圖

討 論

類別變量的結構方程模型處理的是可以轉化為梯階型的觀測變量，類別變量的分類間距既可以相等，也可以不等，至于作為分類基準的潛在連續型變量的意義是什么并不重要，它僅僅是一個工具性假設而已。類別變量的結構方程模型尤其適用于類似李克特量表(Likert scale)等方面的研究，由于需要使用不同的分析技術，應用上受到了一定的限制，但隨著統計軟件的不斷開發，類別變量的結構方程模型的應用也將越來越廣泛，越來越準確。除了LISREL以外，其他包含結構方程模型的軟件也提供了類別變量的結構方程模型分析工具，比如、MPLUS、EQS等等。

在同時涉及不同類型變量的情況下，相關系數變得更加復雜，連續變量間需要估計的是皮爾遜相關系數，類別變量間需要估計的是多項相關系數，類別變量與連續變量間需要估計的是多列相關系數(polyserial correlations)。LISREL軟件中的“PRELIS”可以實現三種不同相關系數的估計，只要在“Data－Define Variables”指令下對變量的類型進行定義就可以了，相關的分析與類別變量結構方程模型的分析方法完全相同。

結構方程模型是一種有效的研究方法和統計技術，在公共衛生領域也有廣泛的應用〔10－12，14〕。如果使用不恰當，就會導致不正確的統計推斷。觀測變量的類型是需要考慮的重要因素之一，它直接影響到分析矩陣的構成和參數的估計方法。

(致謝 本論文的完成得到暨南大學211項目資助以及暨南大學“國家大學生創新性實驗計劃”資助，在此一并表示感謝。)

1.Do Toit S，Do Toit M，Mels G，et al.LISREL for Windows:PRELIS User's Guide.2008，Lincolnwood，IL:Scientific Software International，Inc

2.Browne MW.Asymptotically distribution－free method for the analysis of covariance structure.British Journal of Mathematical and Statistical Psychology，1984(37):62－83.

3.Lowe B，Wahl I，Rose M，et al.A 4－item measure of depression and anxiety:validation and standardization of the Patient Health Questionnaire－4(PHQ－4)in the general population.Journal of Affect Disorders，2010(122):86－95.

4.Jensen LW，Decker L，Andersen MM.Depression and health－promoting lifestyles of persons with mental illnesses.Issues in Mental Health Nursing，2006(6):617－634.

5.Tanaka H，Sasazawa Y，Suzuki S，et al.Health status and lifestyle factors as predictors of depression in middle－aged and elderly Japanese adults:a seven－year follow－up of the Komo－Ise cohort study.BMC Psychiatry，2011(7):11－20.

6.Belloc NB，Breslow L.Relationship of physical health status and health practices.Preventive Medicine，1972(1):409－421.

7.Morimoto K.Lifestyle and health.Japanese Journal of Hygiene，2000(54):572－591.

8.Toda M，Makino H，Kobayashi H，et al.Health－related lifestyle and travel patterns of behavior related to health effects of leisure.Social Behavior and Personality，2007，35(3):287－294.

9.J?reskog KG，S?rbom D.LISREL 8:Structural equation modeling with the SIMPLIS command language.Mooresville，IN:Scientific Software，Inc.1993.

10.張宜民，馮學山.公立醫療機構醫生工作滿意度結構的驗證性因素分析.中國衛生統計，2011，28(1):29－32.

11.張鵬，樓超華，Laurie，等.上海未婚青少年性相關行為影響因素結構方程模型分析.中國衛生統計，2011，28(2):139－141.

12.何勃夫，孫濤，柳曉琳，等.基于結構方程模型的工作生活質量與離職傾向關系的整合模型構建.中國衛生統計，2011，28(2):168－170.

13.李鵬，蔡麗，崔壯.天津市某三甲醫院闌尾炎患者住院費用影因素的結構方程模型分析.中國衛生統計，2011，28(2):161－164.