導彈發射裝置隨動系統模糊神經PID控制器

趙修平，蘇正波，郭 凱，王天輝

（1．海軍航空工程學院 a．飛行器工程系；b．研究生管理大隊，山東 煙臺 264001； 2．海軍裝備部軍械保障部，北京 100841）

某型導彈發射裝置的隨動系統是采用永磁同步電機的一個非線性多變量系統，傳統的PID 控制器難以實現理想的控制效果。隨著控制理論的發展，PID 控制與一些先進的智能控制結合被用于復雜對象的控制中，已成為一個發展方向。如模糊PID 控制就是將模糊控制與PID 控制結合，利用模糊控制的推理能力來自動調整PID 控制參數的。[1-3]但模糊控制的控制規則及隸屬度函數，一旦建立就無法更新，存在控制精度不高等問題。基于神經網絡的PID控制是將神經網絡與PID 控制結合，利用神經網絡的自學習能力來調節PID 參數[4-6]，但神經網絡的結構和權值沒有明確的物理意義，這給神經網絡的設計及初始化帶來很大困難[7]。模糊神經PID 控制是將模糊控制、神經網絡及PID 控制結合起來，利用模糊控制和神經網絡的互補性，設計一種模糊神經控制器，自動調節PID 控制器的參數索算法[8-9]，把一階回溯和最好優先結合起來，以便縮小搜索空間，提高得到滿意解的速度。

1 發射裝置隨動系統的數學模型

某型導彈發射裝置隨動系統是由永磁同步電動機、位置和速度等傳感器、晶體管脈寬調制(PWM)逆變器及控制電路等環節組成。圖1 是具有位置反饋、速度反饋和電流反饋三閉環結構的方位隨動系統原理圖。由文獻[8]可知，其模型近似地看作是一個二階對象：

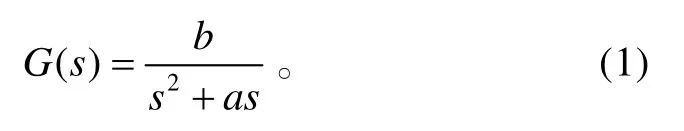
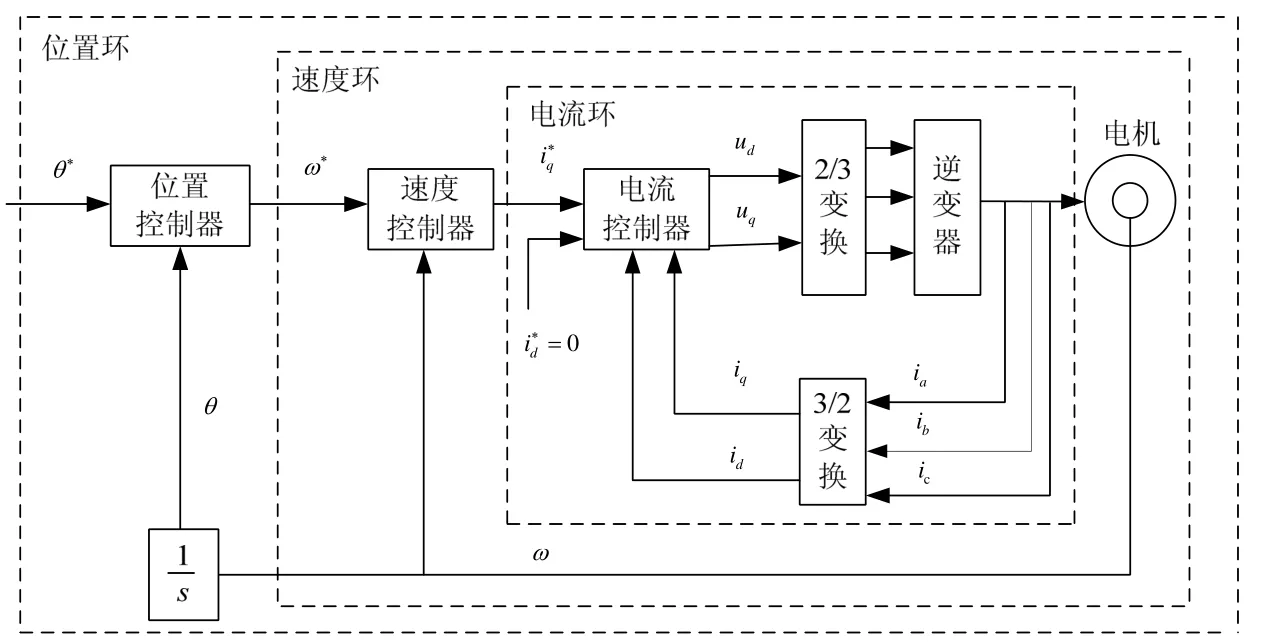
圖1 隨動系統原理圖

2 模糊神經PID 控制器的設計

2.1 模糊神經PID 控制器的結構原理

利用模糊系統和神經系統的等價結構，把模糊控制和神經網絡相結合，構成模糊神經控制器。用模糊神經控制器來對傳統PID 控制器的參數進行調節，從而構成模糊神經PID 控制器。其原理圖如圖2 所示。

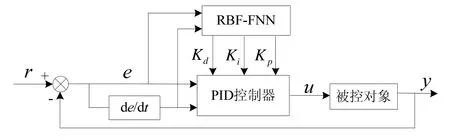
圖2 基于模糊神經網絡的智能PID 控制器的原理圖

模糊神經網絡結構中輸出層的神經元個數應設置為3 個，3 個輸出分別為PID 控制器的參數kp、ki、kd。該隨動系統采用如式(2)所示的增量式PID控制算法，

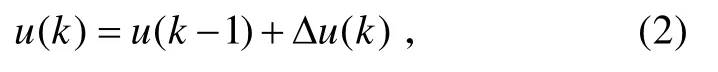
Δu可表示為

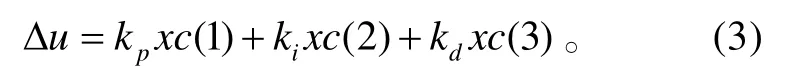
式(3)中：xc( 1) =e(k)；xc( 2) =e(k) ?e(k? 1)；

xc( 3)=e(k)?2e(k? 1)+e(k+ 2)。

2.2 模糊神經控制器的結構

模糊神經控制器是用神經網絡對模糊控制器的隸屬度函數及模糊控制規則進行調整，把誤差e和誤差變化率ec作為系統的輸入量，輸入和輸出變量均劃分為7 個模糊子集，它們的隸屬度函數都用高斯函數表示。模糊神經控制器的網絡結構見圖3。

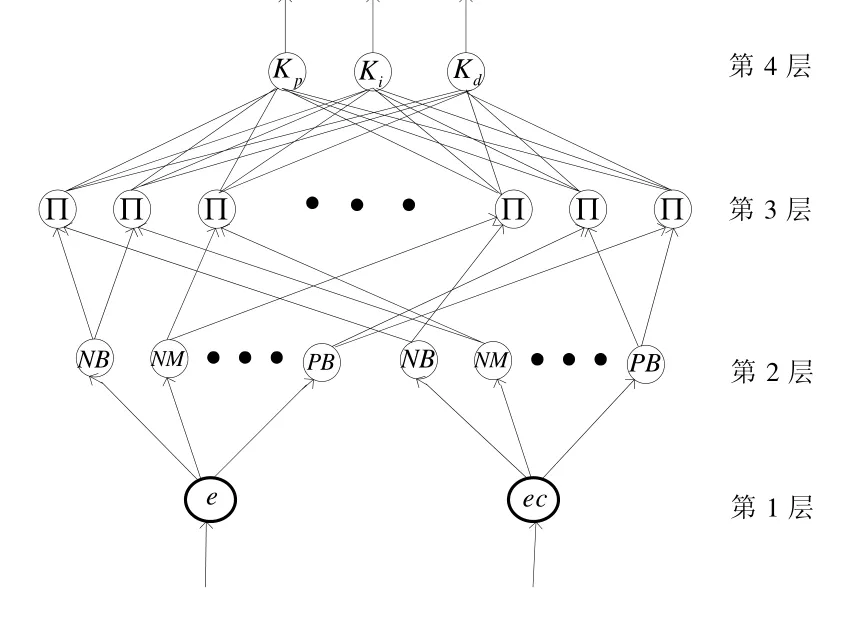
圖3 模糊神經控制器結構圖

該模糊神經控制器有4 層網絡構成，分別為：輸入層、模糊化層、模糊推理層和輸出層。各層的信號傳播及功能如下[9]：

第1 層：輸入層。該層的各個節點直接和輸入量各點連接，將輸入量直接傳到下一層。節點數為2，對該層每個節點i的輸入輸出可表示為

第2 層：模糊化層。該層實現輸入變量的模糊化，完成一個隸屬度函數的計算，計算出變量相對于每個模糊子空間的隸屬度。該層中的每一個節點可代表著與輸入變量相應的模糊語言值，節點數為14。在這一層，采用高斯型函數作為隸屬度函數，cij和bij分別是第i個輸入變量第j個模糊集合的隸屬度函數的均值和標準差。

本層的隸屬度函為

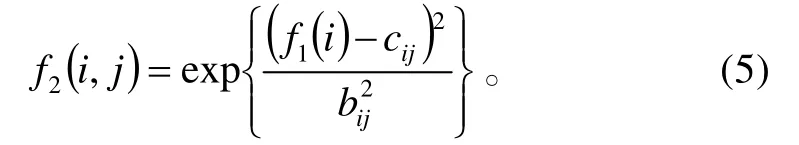
式(5)中：i=1,2；j=1,2, … ,7；f(i)表示輸入變量。

第3 層：模糊推理層。模糊推理層是網絡中的重要部分，它聯系著模糊推理的前提和結論，實現網絡的模糊映射。模糊推理層是通過與上一層的連接來實現模糊規則的匹配，該層的各個節點之間可實現模糊運算，即利用各個模糊節點的組合可求出相應的點火強度，然后進行歸一化處理。該層節點為49，通過式(6)得到每個節點的輸出。

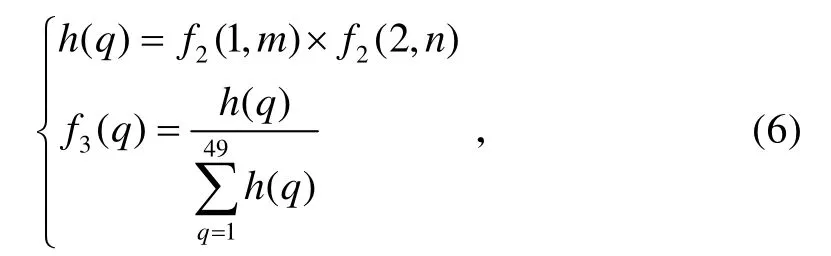
式中：m=1,2, … ,7；n=1,2, … ,7；f(1,m) 和f(2,n)表示輸入變量，即第2 層輸出量。

第4 層：輸出層。該層主要計算模糊神經網絡的輸出值，經過解模糊化將最終結果輸出。該層有3 個神經元節點，節點的輸出分別為kp、ki、kd的整定結果。這里有一個第3 層跟本層的連接權值矩陣wpq，它是一個49 行3 列的矩陣。

本層的輸出值就是將權值矩陣和第3 層的輸出相乘。即，

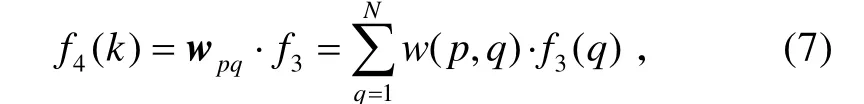
式中：p=1,2,3，q=1,2,… , 49，N=49。

2.3 模糊神經控制器的參數學習

對于所設計模糊神經控制器的參數學習過程就是對權值矩陣wpq和高斯函數寬度cij和中心值bij的參數調節過程。對權值矩陣wpq的調節實現對模糊規則的調節，對高斯函數參數cij和bij的調節實現隸屬度函數形狀和位置的調節。

通過對參數的調節使目標函數達到最小，這里取目標函數為

式(8)中：θ*為隨動系統的期望位置輸出，即伺服系統的輸入；

θ為隨動系統的實際位置輸出。

為了使系統的實際輸出θ最逼近于系統的期望輸出θ*，必須讓目標函數E的值達到最小，這里選取Delta 學習規則來計算Δwpq、Δbij和Δcij。

Δwpq可表示為：

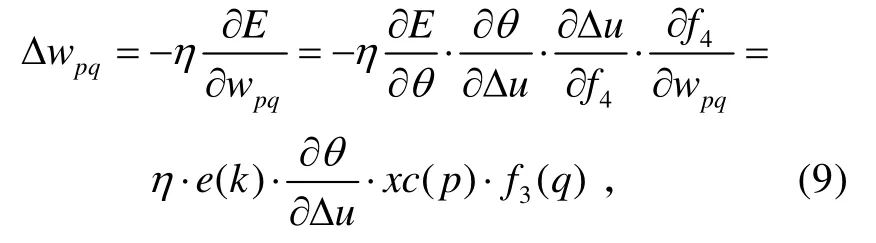
式中，η為學習速率。

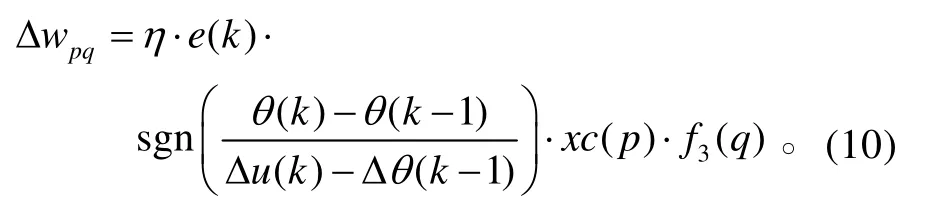
同理可得：

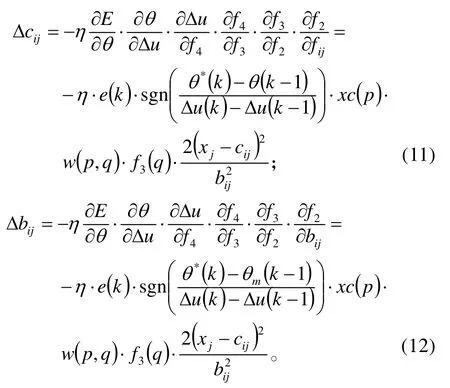
采用一階梯形尋優算法可以求得：

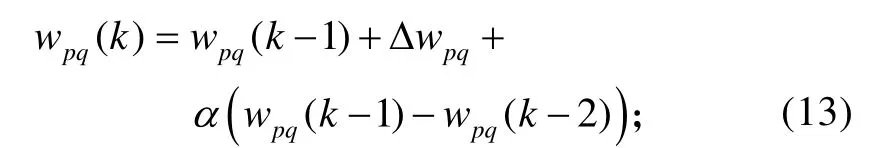
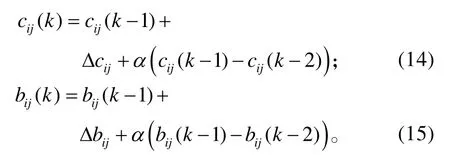
式(13)~(15)中：k為控制器的迭代步驟；α為學習動量因子。

3 系統仿真

3.1 建立仿真模型

在該隨動系統中，位置環的作用就是保證系統靜態精度和動態跟蹤的性能，這直接關系到發射裝置隨動系統的穩定與高速運行，對整個系統的動靜態性能具有重要影響[11]。電流環、速度環為隨動系統的內環，傳統的PI 控制器可以滿足該隨動系統對于電流和速度的響應需求[12]。因此，本文主要是對該隨動系統的位置環的控制進行研究，對電流環和速度環采用 PI 控制，對永磁同步電機控制采用id= 0的矢量控制。

本文采用matlab/simulink 對該隨動系統進行仿真研究，整體的仿真框圖如圖4 所示。

模糊神經PID 控制器利用s 函數編寫，集成為一個模塊。為了與模糊自適應控制效果進行對比設計傳統PID 控制器。經過不斷的測試，在傳統的PID控制器中取參數kp= 24、ki= 6、kd= 4時，系統可以達到較好的效果。在對比閉環系統進行仿真前，需要對simulink 仿真環境進行設置，選取算法為ode23t，可變步長，相對誤差為0.001 s，仿真時間為10 s，啟動仿真結束后，得到仿真曲線。

3.2 仿真結果分析

在t= 0時系統有幅值為100 的階躍輸入，采用模糊神經PID 控制器該伺服系統的位置響應曲線如圖5 所示；采用傳統PID 控制器該伺服系統的位置響應曲線如圖6 所示。從圖5 和圖6 的對比可以看出在模糊神經PID 控制器下，系統的快速性明顯優于傳統的PID 控制器，且系統沒有超調。

在t= 7時，給系統以一定的負載，其響應曲線如圖7 及圖8 所示。從圖7 和圖8 的對比可以看出，在模糊神經PID 控制器的作用下，其隨動系統的魯棒性要優于傳統的PID 控制器。

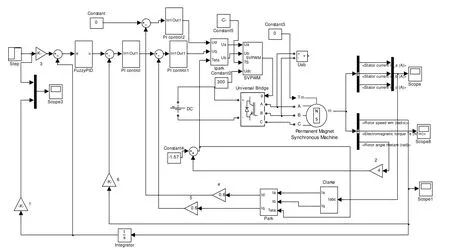
圖4 隨動系統的整體仿真模型

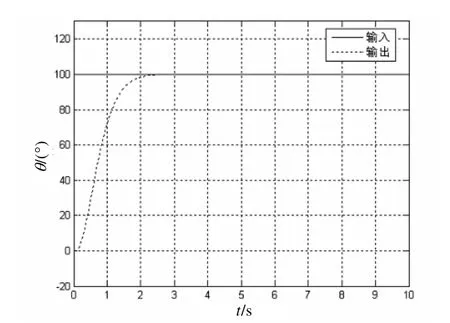
圖5 基于模糊神經網絡PID 控制器位置階躍響應曲線

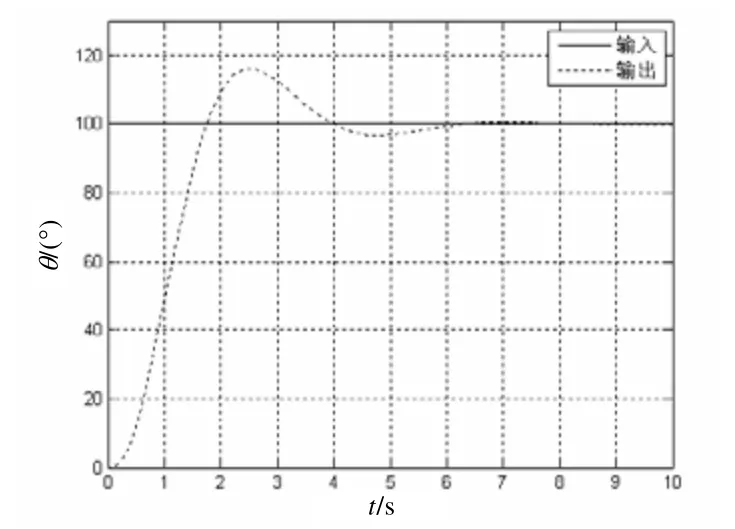
圖6 傳統PID 控制器階躍響應曲線

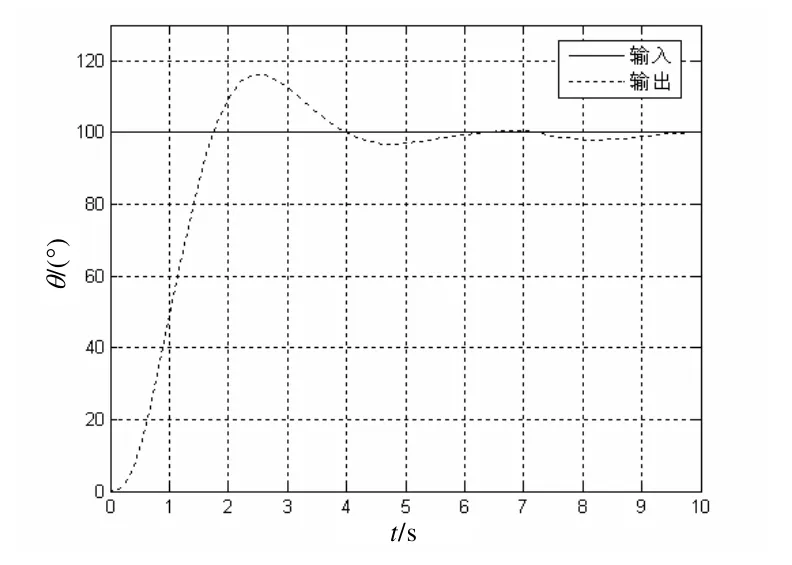
圖7 傳統PID 控制器下負載干擾階躍響應曲線

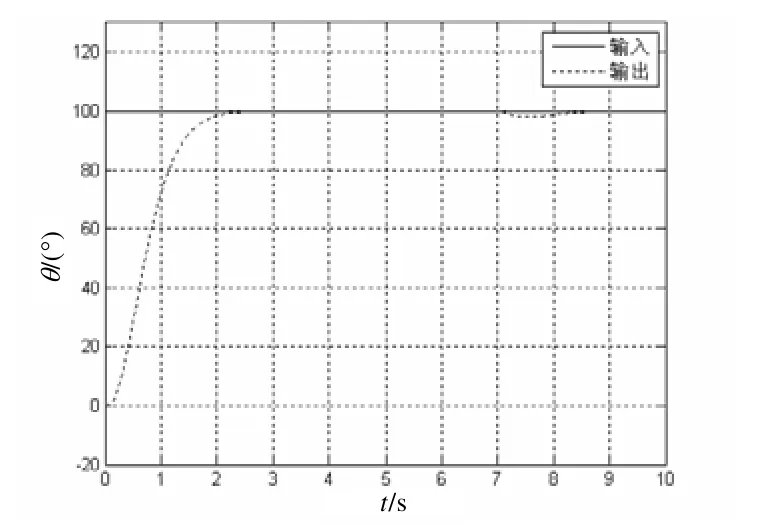
圖8 基于模糊神經網絡的智能PID 控制器 負載干擾階躍響應曲線

4 結論

本文將模糊控制、神經網絡及傳統的PID 控制相結合，根據某型導彈發射裝置的隨動系統模型，設計了模糊神經PID 控制器。通過和傳統PID 控制器的仿真對比看出，在該隨動系統中用模糊神經PID 控制器，其動態性能和魯棒穩定性有顯著改善。

[1] 姬偉, 李奇. 自適應模糊PID 控制器在跟蹤瞄準線穩定系統中的應用[J]. 控制理論與應用, 2008,25(2): 278-282.

[2] 李曉強, 王丹, 黃加亮, 等. 一種非線性時滯系統的魯棒性模糊自適應控制[J]. 控制與決策, 2010,25(7): 1045-1049.

[3] SHAYANFAR H A, JALILI A. Multi-stage fuzzy PID power system automatic generation controller in deregulated environments[J]. Energy Conversion and Management, 2006,47:2829-2845.

[4] 姜峰, 段鎖林. 基于CMAC 的PD 控制在電液伺服系統中的應用[J]. 計算機仿真, 2011,28(4):152-155.

[5] 王軍, 張幽彤, 王憲成, 等. 神經網絡結構PID 方法在電液供油提前器中的應用研究[J]. 兵工學報, 2008,29(10):1163-1166.

[6] YE JUN. Adaptive control of nonlinear PID-base analog neural networks for a nonholonomic mobile robot[J]. Neurocomputing, 2008,71:1561-1565.

[7] 程啟明, 程尹曼, 鄭勇, 等. 基于模糊徑向基函數神經網絡的PID 算法球磨機控制系統研究[J]. 中國電機工程學報, 2009,29(35):22-28.

[8] 王天輝, 趙修平, 徐廣. 某型導彈發射裝置伺服系統的滑模控制器設計與仿真[J]. 艦船電子工程, 2011, 31(6):189-191.

[9] LIN F J, WAI R J, LEE C C. Fuzzy neural network position controller for ultrasonic motor drive using push-pull DC-DC converter[J]. IEEE Proceedings Control Theory Application, 1999,146(1):99-107.

[10] 王瑞明. 交流伺服驅動系統新型控制策略研究[D]. 杭州: 浙江大學, 2005.

[11] 尹霞, 黎亞元, 萬志偉．數控伺服系統模糊PID 控制仿真研究[J]. 裝備制造技術, 2008(10):103-104.

[12] 陳時伯. 電力拖動自動控制系統[M]. 北京: 機械工業出版社, 2010:21-35.