艦空導彈發射時間窗解算模型仿真

周紹磊，尹高揚，張文廣

（海軍航空工程學院 a.控制工程系；b.研究生管理大隊，山東 煙臺 264001）

Khosla在用一種混合遺傳算法來解決動態武器目標分配問題時，提出了“時間窗(Time Window)”的概念以描述時間約束[1-2]。蔡懷平將時間窗口概念引入武器目標分配(Weapon Target Assignment，WTA)模型，建立了動態 WTA的約束滿足問題(Constraint Satisfaction Problem，CSP)模型[3]。在WTA中，每個“武器目標對(Weapon-Target Pair)”都存在一個武器射擊時間窗口，它定義了該武器對該目標射擊的最早和最遲時間，產生該武器目標分配的時間要早于最遲發射時間。

本文在文獻[4]的基礎上，同時考慮了目標機動的影響，建立了艦空導彈發射時間窗解算模型，并運用計算機技術對模型進行仿真模擬，驗證了模型的合理性和有效性。

1 問題描述

設目標到達武器單元的發射區遠界、近界的時間分別為ty、tj。目標在武器單元發射區的停留時間，即為武器單元對目標的打擊時間窗口，

對艦空導彈的發射時間窗的解算可以按以下步驟來進行：

① 武器單元發射區遠近界解算；② 反艦導彈目標以比例導引朝武器單元機動飛行；③ 目標飛臨武器單元發射區遠近界的時間解算。

2 艦空導彈發射時間窗解算模型

2.1 艦空導彈武器單元發射區解算

目標到達武器單元的發射區遠界、近界的時間是發射時間窗口計算的基礎。艦空導彈發射區，就是在發射導彈瞬間，能使導彈在殺傷區內與目標相遇的所有目標位置點所構成的空間區域。即只有目標處在發射區內發射導彈，才能保證導彈有效地殺傷目標(給定殺傷概率范圍)。艦空導彈發射區是在殺傷區的基礎上確定的。殺傷區是指防空導彈發射后，能以不低于某一給定概率殺傷空中目標的空域，是防空導彈武器系統戰斗綜合性能的重要指標之一，它決定了武器系統的使用射程、高度和航路捷徑。表征殺傷區的主要參數有高界Hmax、低界Hmin、遠界 Rsy、近界 Rsj和側近界 Rs'j。發射區的大小和形狀與目標的速度和運動軌跡、殺傷區的大小和形狀、導彈飛到殺傷區的時間等因素有關。對于每種型號的艦空導彈都有其戰技指標，其殺傷區大小和形狀是確定的。

研究發射區的目的，就是為了確定艦空導彈的發射時機。發射區通常以遠界 Rfy、近界 Rfj、高界Hmax、低界Hmin和側近界 R'fj來表示。確定發射區的方法是：從殺傷區任一點出發向目標飛行的相反方向移動一段距離(導彈飛至遭遇點時間內目標運動的距離)就得到此點在發射區所對應的點。為了研究方便，用航路捷徑為零的鉛直平面切割發射區，得到艦空導彈的垂直發射區，垂直發射區如圖1所示。

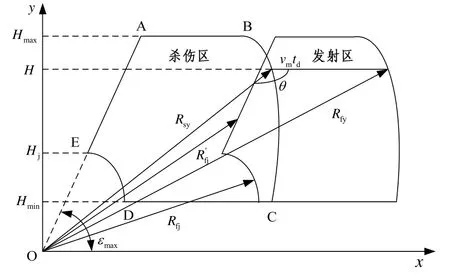
圖1 垂直發射區

對艦空導彈武器系統而言，能夠實時影響艦載防空導彈發射區的參數主要是空中目標的速度 vm、高度Hm、航路捷徑Pm等飛行諸元、殺傷區的大小和形狀(遠界 Rsy、近界 Rsj、最大高低角 εmax、最大航路角 qmax)和艦載防空導彈飛至遭遇點的時間 td。即艦載防空導彈武器的發射區遠界和近界斜距是空中目標諸元和艦載防空導彈特性的函數：

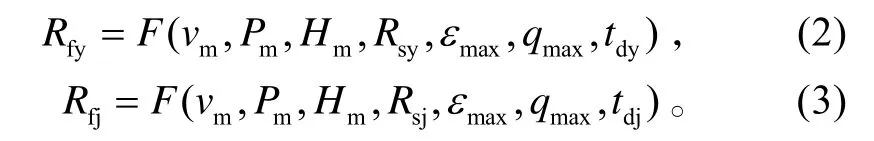
假設目標以航向 Cm、速度 vm、航路捷徑Pm、高度Hm來襲，態勢如圖2所示。

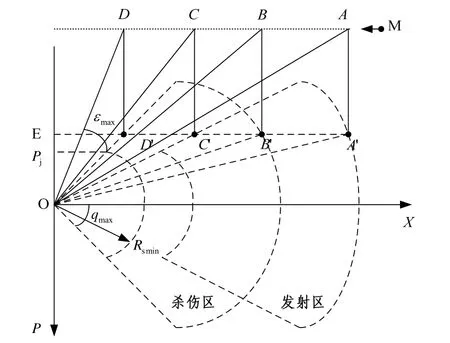
圖2 水平發射區

圖2中，A為發射區遠界點，B為殺傷區遠界點，C為發射區近界點，D為殺傷區近界點，(A',B ',C ',D ')為(A,B,C,D)在水平面上的投影。艦空導彈的平均速度為vd。

在△O BB'中，殺傷區遠界在水平面上的投影距離為：

艦載防空導彈飛至殺傷區遠界遭遇點的時間為：

在△O B ' A'水平殺傷區上求得發射區遠界的投影距離為：

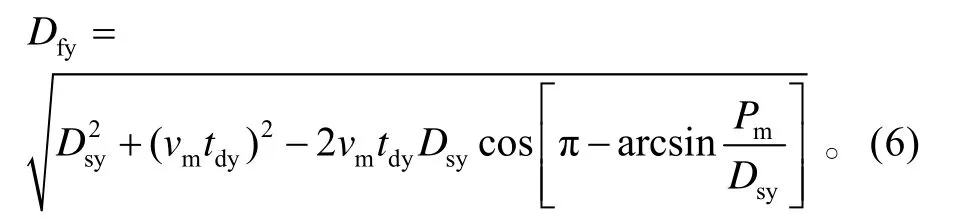
在△O AA'中，發射區遠界為：

從垂直殺傷區中可知，Hj是殺傷區最近界對應的最大高度。

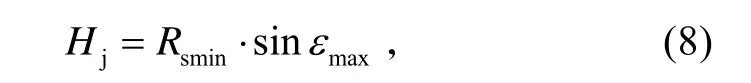
式中，Rsmin為殺傷區最近界斜距。從圖2可知，Pj是殺傷區最近界對應的最大航路捷徑。

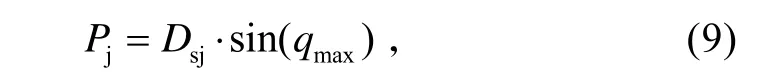
式中，Dsj為殺傷區近界在水平面上的投影距離。

1) Hm＜Hj時。

①當Pm＞Pj時，殺傷區近界值取側近界，近界在水平面上的投影距離為：

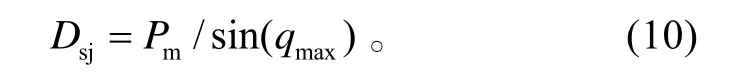
艦載防空導彈飛至殺傷區側近界遭遇點的時間為：

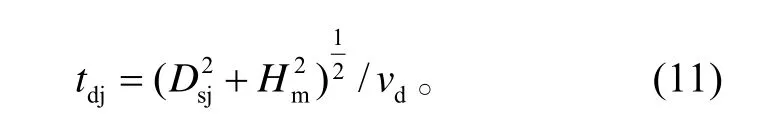
在△O D 'C 中求得發射區側近界的投影距離為：

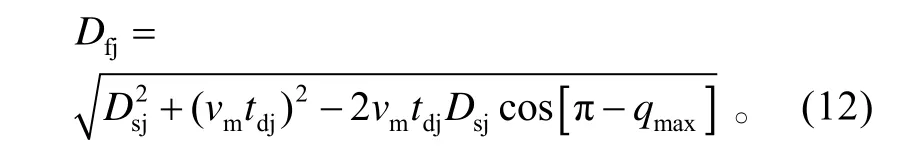
在△O CC'中求得發射區側近界為：

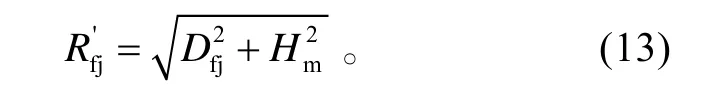
②當Pm≤Pj時，近界在水平面上的投影距離為：

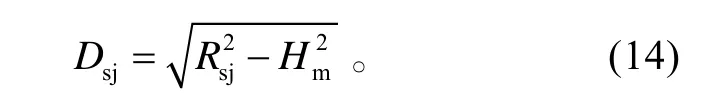
艦載防空導彈飛至殺傷區最近界遭遇點的時間為：

在△O D 'C 中求得發射區近界的投影距離為：

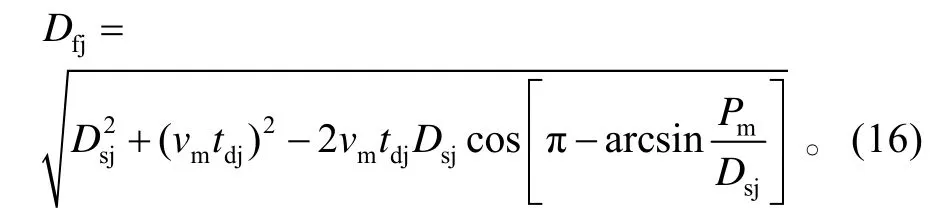
在△O CC'中求得發射區近界為：

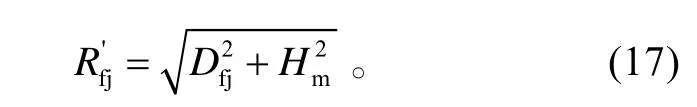
2) Hm≥ Hj時。

殺傷區近界值取側近界，殺傷區近界斜距為：

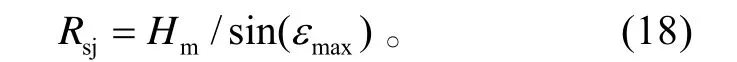
艦載防空導彈飛至殺傷區側近界遭遇點的時間為：

近界在水平面上的投影距離為：

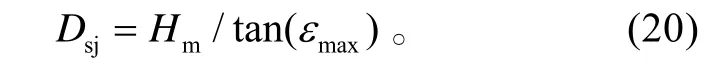
在△O D 'C 中求得發射區側近界的投影距離為：

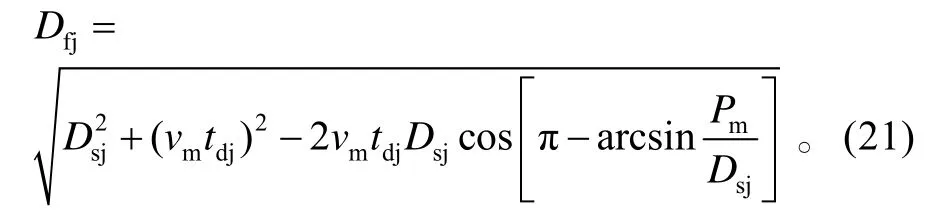
在△O CC'中求得發射區側近界為：

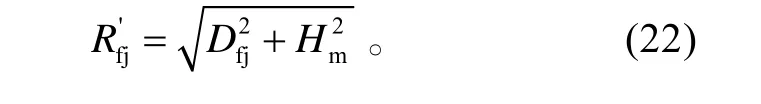
2.2 艦空導彈發射時間窗解算

圖3中，A為發射區遠界點，C為發射區近界點，K為目標當前位置點，(A',C ',K ')為(A,C,K)在水平面上的投影。其中 AA'=KK '=Hm，O A=Rfy，OA '=Dfy，OC=Rf'j，目標當前距離OK=L。目標距離艦艇的水平距離為OK '=DL。

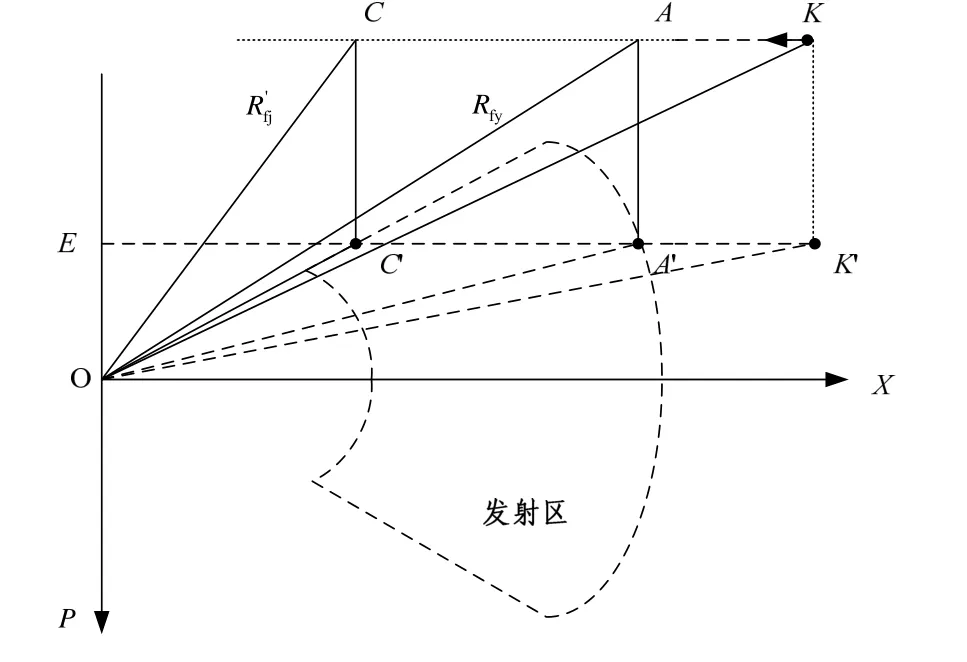
圖3 時間窗解算

確定目標到達武器單元的發射區遠界、近界時間的方法是：從艦載雷達生成某時刻目標的航向數據，沿著目標航向角方向出發向武器單元的發射區遠、近界移動一段距離(來襲導彈目標從當前位置飛至發射區遠近界的時間內目標運動的距離)，直到與之相交。目標飛至發射區遠近界交點的時間差即為對于該目標艦空導彈的發射時間窗。為了便于計算，先假設目標沿水平直線飛行。

目標從當前位置飛至艦空導彈發射區遠界的距離在水平面的投影：

在△O A' E中，

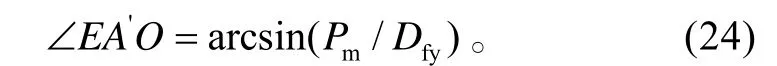
在△O A' K '中，

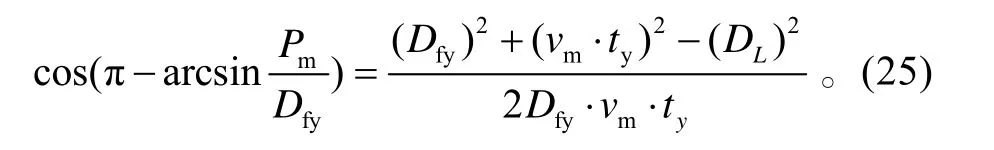
解上式，即可求得目標飛至艦空導彈發射區遠界的時間 ty。

目標從當前位置飛至艦空導彈發射區近界的距離在水平面的投影：

在△O C 'E中，

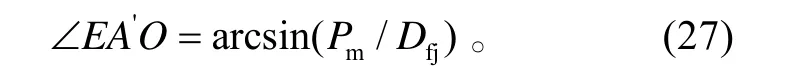
在△O C 'K '中，

解上式，即可求得目標飛至艦空導彈發射區遠界的時間 tj。則目標在武器單元發射區的停留時間，即武器單元對目標的打擊時間窗口為：

2.3 目標機動情況下發射時間窗解算

在2.2節中，目標是從當前位置開始，按目標航向水平直線飛行。在實際作戰中，來襲反艦導彈的航向角、高度和速度等都是時刻改變的。因此，應根據目標實際進入艦空導彈發射區遠、近界的時間，來得到對目標的打擊時間窗。

圖4描述了來襲導彈目標與艦艇之間的相對運動關系[5-8]。

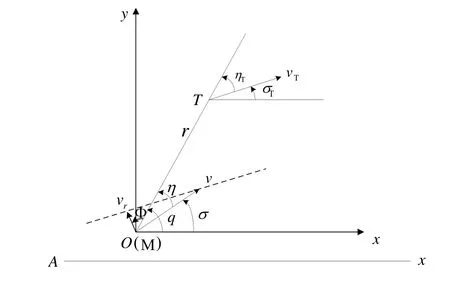
圖4 來襲導彈與艦艇的相對運動關系示意圖

相對運動方程為：

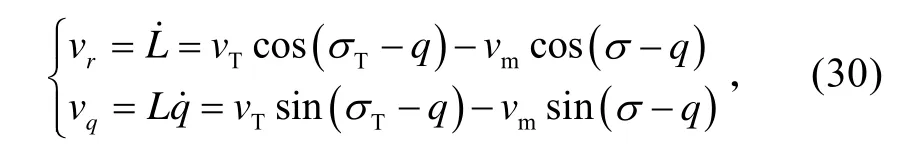
式中：vr、vq分別為來襲導彈目標與艦艇的接近速度和視線法向速度；vm、vT分別為導彈速度和艦艇速度；q是艦艇目標線與基準線之間的夾角；σ、Tσ分別為導彈、艦艇速度矢量與基準線之間的夾角。

假設目標以比例導引的方式襲來，比例導引關系方程為：

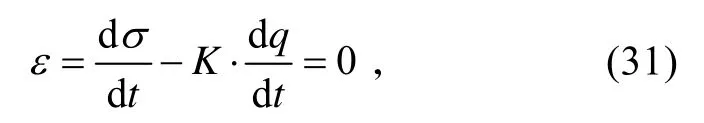
式中，K為比例系數[9]。

艦載雷達系統以時間周期T 更新目標信息。通過對幾個周期內目標信息的擬合，可以得到目標的來襲軌跡，估計目標的比例導引系數，并對未來航跡進行預測。得到目標的預測航跡后，即可計算目標與艦空導彈發射區遠近界的交點和飛至遠近界交點的時間，從而解算武器單元對目標的打擊時間窗口。

3 仿真實例

目標初始數據見表1，基于2.2節中目標保持初始航向水平直線飛行直接計算得到的發射時間窗解算見表2。

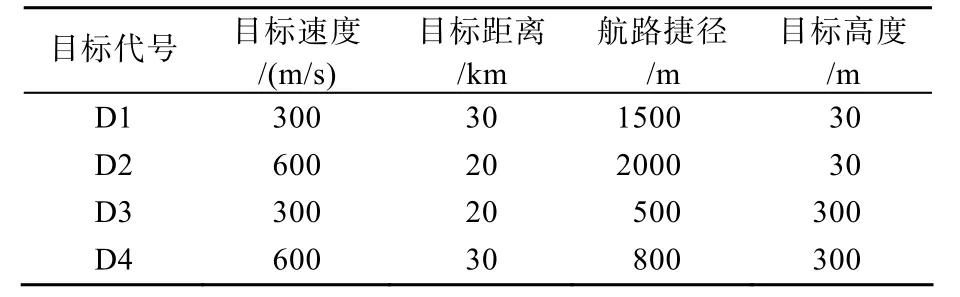
表1 目標初始數據

表2 解算結果

基于2.3節中考慮目標機動飛行計算得到的發射時間窗解算見表3。

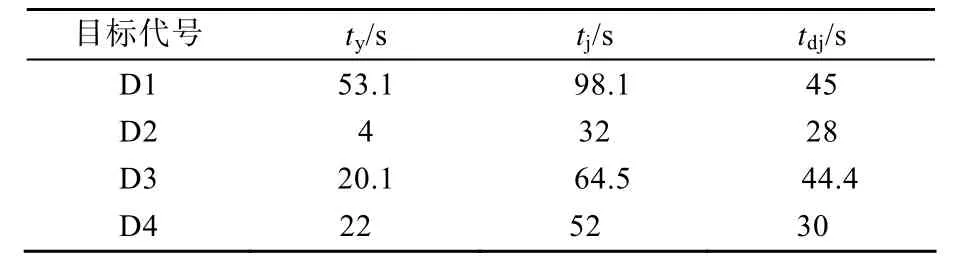
表3 解算結果

用Matlab 進行編程計算，目標飛行預測軌跡如圖5所示：

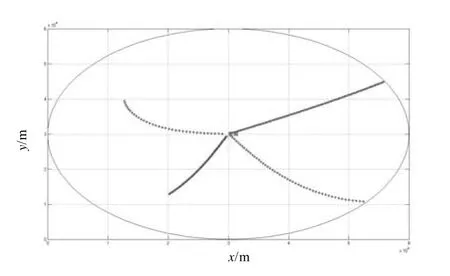
圖5 來襲導彈預測軌跡

由表2和表3可知，目標保持初始航向水平直線飛行穿過艦空導彈發射區遠近界的時間較短，目標機動飛行穿過艦空導彈殺傷區的時間稍長。目標機動飛行到達艦空導彈殺傷區遠界時，導彈已經鎖定了艦艇目標，以極小的航路捷徑朝艦艇襲來，由圖3和圖5可知，目標斜穿發射區遠近界的時間要長于水平直線穿過的時間，仿真計算結果合理客觀。

4 結束語

研究艦空導彈的發射時間窗可以確定艦空導彈的發射時機和計算艦空導彈攔截次數，同時在進行動態目標分配時，將時間窗作為時間約束，可以增強目標分配的合理性和實時性。從仿真結果可知，所建模型合理，所得數據可作為艦空導彈的威脅評估和目標分配的依據，并用于確定艦空導彈的發射時機，指導防空作戰指揮決策。由于根據艦載雷達的周期性數據預測目標的航跡具有一定的誤差，有待進一步研究。

[1]KHOSLA D.Hybird genetic approach for the dynamic weapon-target allocation problem[C]//Proceeding of SPIE.2001,4396∶248-263.

[2]劉傳波,邱志明,吳玲.動態武器目標分配問題的研究現狀與展望[J].電光與控制,2010,17(11)∶12-15.

[3]蔡懷平,陳英武,刑立寧.SVNTS算法的動態武器目標分配問題研究[J].計算機工程與應用,2006,17(3)∶559-565.

[4]鐘志通,徐德民,周州.艦載防空導彈發射區解算模型[J].火力與指揮控制,2009,34(5)∶53-57.

[5]萬自明,溫羨嶠.地空導彈武器系統的威脅判斷及火力分配模型[J].系統工程與電子技術,1988,10(3):80-83.

[6]徐品高.點防空導彈武器系統攔截方案與火力分配[J].戰術導彈技術,1993(1):7-17.

[7]韓松臣.導彈武器系統效能分析的隨機理論方法[M].北京:國防工業出版社,2001:200-205.

[8]陳立新.防空導彈網絡化體系效能評估[M].北京:國防工業出版社,2007:218-220.

[9]楊軍.導彈控制原理[M].北京:國防工業出版社,2010:123-125.