5000m特大跨度懸索橋空氣動力穩定性能理論研究

邵亞會，葛耀君，柯世堂，楊詠昕

（1.合肥工業大學土木與水利工程學院，合肥 230009；2.同濟大學土木工程防災國家重點實驗室，上海200092）

0 引 言

二維顫振分析基于片條理論，用廣義質量模擬全橋真實狀態的質量系統，用節段模型在氣動力和自身重力作用下的受力狀態和運動方式模擬全橋真實的受力狀態，不考慮風荷載和結構的三維效應。為考察三維效應，有必要引入三維橋梁顫振分析。1989年，Agar［1］基于Scanlan的線性自激力模型和顫振分析理論，提出了將顫振問題簡化為求解非對稱實矩陣的特征值問題，采用雙參數搜索迭代求解；Beith也提出了相同的方法［2］。1992年，Namimi［3］提出了顫振分析的PK－F法，同濟大學程韶紅、張新軍等人沿用了此法。1994年，陳政清［4］提出多模態單參數搜索顫振分析方法，將顫振問題轉化為求解復矩陣的廣義特征值問題，且認為橋梁顫振中高階模態的參與具有有利與不利雙重效果，該方法能方便地求解顫振臨界風速和頻率，但不能描述顫振發生的全過程。1996年，Jain［5］也將顫振問題轉化為求解矩陣特征值問題，側重于求解特征多項式的實部和虛部方程。1995年，Miyata［6－7］和Yamada首次提出了顫振全模態分析方法，但沒有考慮結構阻尼的影響。Dung［8］在1998年發展了該方法，仍無法有效考慮結構阻尼的影響。2000年，葛耀君［9］提出了大跨度橋梁三維顫振分析的全模態方法，考慮了結構阻尼的影響，同時也將顫振頻域分析方法提高到了一個新的高度，自此之后關于顫振頻域方面的研究多是基于此的細化和延伸。2000年之后，國內外諸多學者繼續對大跨度橋梁的顫振問題進行了大量研究［10－13］，通過自主研發軟件和嫁接商業軟件進行二次開發，豐富了大跨度橋梁三維顫振研究，不同之處在于針對不同的研究對象，考慮了不同的求解過程和技巧。

已有文獻多是針對跨度在1500m以下的大跨度懸索橋進行氣動穩定性研究，而對于跨度超過1500m，甚至達到5000m的特大跨度懸索橋研究成果較少，可供參考的結論不多。為此，將在已有三維頻域全模態顫振分析方法基礎上，進行細化和拓展，考慮三方向氣動導數的影響、靜風荷載非線性的影響、幾何非線性的影響、各種風荷載隨高度的梯度影響等因素，研究5000m特大跨度懸索橋的三維空氣動力穩定性能，并與風洞試驗結果和二維顫振分析結果進行對比，從三維顫振穩定、三維靜風穩定的角度，進一步論證特大跨度懸索橋在5000m跨度范圍的可行性。

1 全模態顫振分析方法

1.1 顫振基本方程

處于風環境中的橋梁結構的動力平衡方程可以表示為：

［Ms］結構總體剛度矩陣；［Cs］結構總體阻尼矩陣；［Ks］結構總體剛度矩陣，［Ks］＝［Ke］＋［Kg］，為彈性剛度矩陣和幾何剛度矩陣的和；｛F｝自激氣動力等效荷載，｛F｝＝｛Fd｝＋｛Fs｝＝［Ca］＋［Ka］｛Y｝；｛Fst｝為靜風荷載；｛Fa｝為慣性力；｛Y｝結構位移向量。

在進行顫振分析時，將結構自身重力和靜風荷載的作用等效為懸索橋結構的預應力，進行有預應力的模態分析，將各參數帶入（1）式后，可以得到：

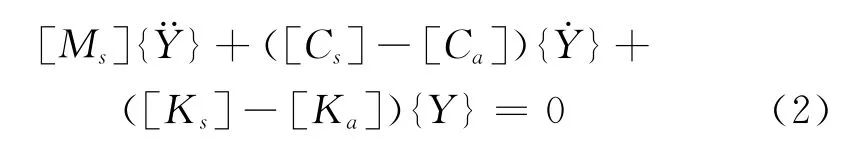
令｛Y｝＝｛φ｝eet，則有：

只有當方程左端的矩陣非奇異時方程（2）才具有非平凡解。實際上這就是一個n次特征值問題。求解該方程將得到2n個特征值和對應的特征向量。方程（2）的通解可以表達為2n個解的疊加：

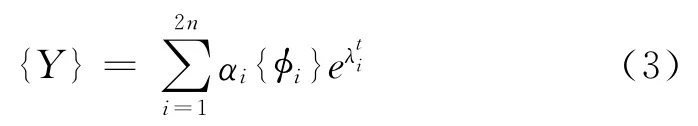
對應復共扼特征值對的分量為：

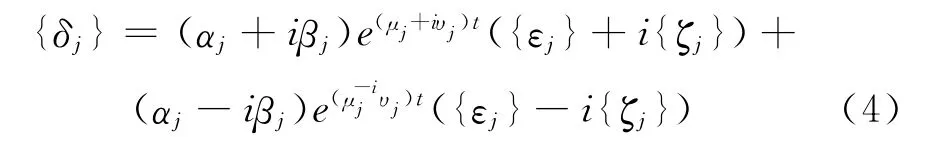
如果所有特征解復共扼成對的，則式（4）可以寫成如下形式

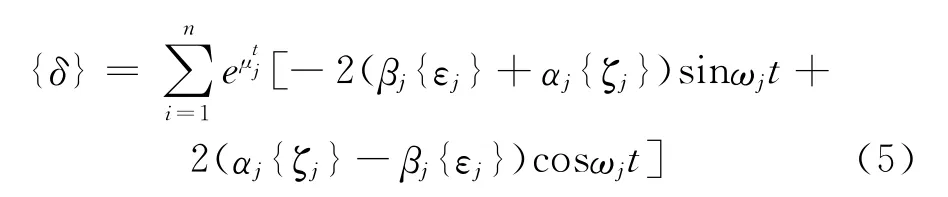
式中，當ui為負時表明系統振動收斂。當ui為正時表明系統顫振發散，此時顫振的圓頻率為Wj。

1.2 風荷載的處理

Scanlan建立了橋梁結構的分離流扭轉顫振理論，建議用6個實函數的顫振導數表示鈍體氣動自激力的公式。近年來，人們逐漸注意到橋梁斷面側向位移對其氣動性能的影響，為此，Sarka和Jones［5］將該氣動力模型予以推廣，考慮了橋梁斷面側向位移對其氣動性能的影響，提出了用18個顫振導數表示的氣動力公式。在無風洞試驗結果的情況下，按照擬靜力理論得到的側向導數如下［14－16］：

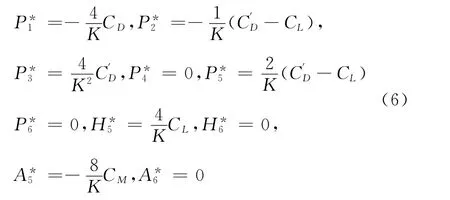
對于纜索氣動力，考慮了主纜和吊桿的自激氣動力、靜風荷載，以及自激氣動力和靜風荷載隨高度的變化，如圖1所示。纜索所受的氣動力表現為正的氣動阻尼，顫振導數只與阻力系數有關，對圓形纜索的阻力系數均取為0.7，纜索的孔隙率取為20%，即在纜索凈截面面積的基礎上考慮20%的面積放大系數。

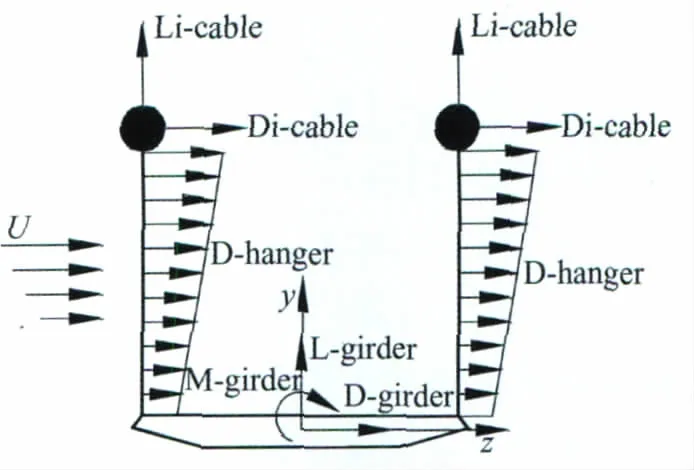
圖1 纜索和吊桿風荷載示意圖Fig.1 Wind loads on cable and hangers

結構阻尼的處理，按照經典瑞利阻尼來考慮，如式（7～8）所示。

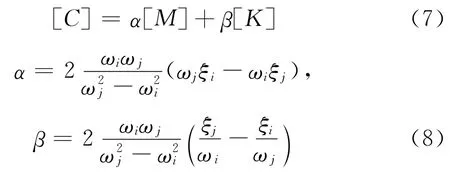
其中，［C］為結構阻尼矩陣，［M］為結構質量矩陣，［K］為結構剛度矩陣，α、β分別為瑞利阻尼系數；ωi、ωj分別為結構第i階和第j階振動圓頻率，ξi、ξj分別為結構第i階和第j階振動阻尼比。

基于上述顫振基本方程和風荷載處理方式，實現了特大跨度懸索橋三維頻域顫振的全模態分析方法。該方法有以下重要特點：（1）可以同時考慮豎向導數、側向導數和扭轉向導數對顫振的影響。側向導數的取值法則如前文所示，按照準定常原則取值。（2）可以同時考慮加勁梁和纜索系統的靜風荷載，并考慮風荷載隨高度變化的梯度變化。（3）精細化地考慮了主纜和加勁梁吊桿的自激力和靜風荷載，主纜和吊桿的受力面積按照毛截面面積取值，主纜的孔隙率為20%。（4）可以同時考慮特大跨度懸索橋的幾何非線性，靜風荷載的非線性。

2 5000m懸索橋顫振性能分析

2.1 顫振風速與頻率

采用三維全橋全模態頻域顫振分析方法，和風洞試驗識別的顫振導數以及三分力系數，對兩種加勁梁方案的特大跨度懸索橋進行了三維全橋顫振分析，每種方案各計算了4種矢跨比的分方案。以窄開槽方案為例，主要分析結果如表1所示，需要說明的是風洞試驗表明，上穩定板的顫振控制效果最好，這里只給出此方案的三維分析結果。顫振計算過程中考慮的主要因素包括：（1）豎向導數、側向導數和扭轉向導數；（2）加勁梁和纜索系統的靜風荷載，并考慮風荷載隨高度變化的梯度變化，以及由靜風荷載引起的初始迎角；（3）加勁梁和纜索系統的自激力荷載；（4）顫振導數隨風迎角的非線性變化；（5）分別搜索了加勁梁正對稱和反對稱扭轉顫振的顫振臨界風速和顫振形態，以期對特大跨度懸索橋的顫振性能有更為全面的認識和把握。

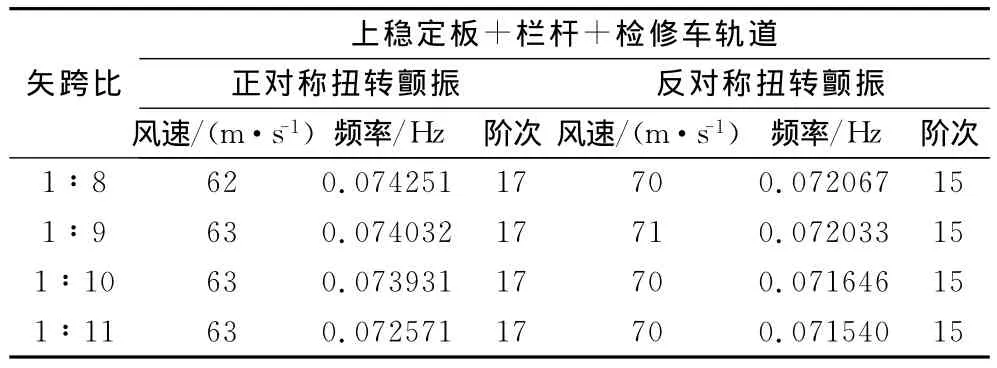
表1 窄開槽方案三維顫振分析結果Table 1 Three dimensional flutter analysis for narrow slotted scheme

研究發現：

（1）對于上水平穩定板、防撞護欄和檢修車軌道組合方案的窄開槽加勁梁懸索橋方案，加勁梁正對稱扭轉顫振的臨界風速為63m／s，反對稱扭轉顫振臨界風速為70m／s，與矢跨比無明顯關系。

（2）顫振頻率隨矢跨比減小而降低，這與二維顫振分析的結論一致；反對稱扭轉顫振頻率均低于同矢跨比的正對稱扭轉顫振頻率；正對稱扭轉顫振發生的模態均為第17階復模態，反對稱扭轉顫振發生的模態為第15階復模態，與矢跨比無關。

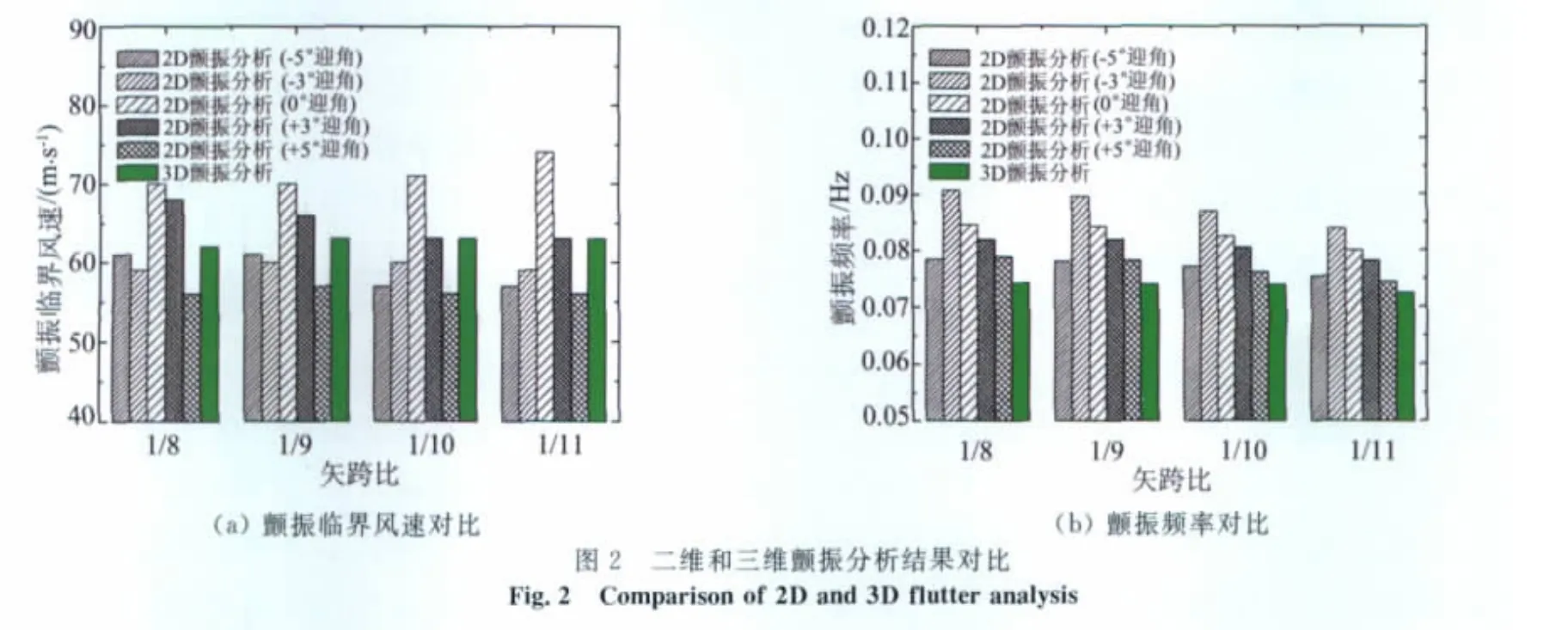
（3）二維和三維顫振分析結果的對比發現，如圖2所示，二維顫振分析在不同迎角時的顫振臨界風速和頻率離散度較大，三維顫振分析中自動考慮了靜風引起的附加迎角的變化，其顫振臨界風速大于60m／s，0°迎角時的二維顫振臨界風速與三維顫振臨界風速較接近。

（4）風洞試驗、二維和三維顫振分析結果均證明矢跨比對顫振分析結果的影響較小，因此在設計跨度為5000m的懸索橋時，不必刻意選擇矢跨比。

同理，研究證明寬開槽加勁梁方案的顫振臨界風速均大于80m／s，顫振形態的變化規律與窄開槽方案類似，在此不詳述。

2.2 顫振形態

圖3為窄開槽方案三維全橋顫振分析獲得的顫振形態，以矢跨比1∶10和1∶11為例，其余矢跨比的顫振形態與其相似，在此予以省略。

研究發現：

（1）顫振形態：最先出現的顫振形態均為加勁梁第一階正對稱扭轉為主、豎彎向自由度強烈參與的顫振形態，加勁梁側向振動參與程度較小，反對稱扭轉顫振晚于正對稱扭轉顫振出現，這種現象與矢跨比的變化無關。

（2）反對稱扭轉顫振形態：反對稱扭轉顫振形態以加勁梁的第一階反對稱扭轉振動為主，矢跨比為1∶8，1∶9，1∶10時，主要參與的豎向振動為加勁梁第一階反對稱豎彎振動，矢跨比為1∶11時，主要參與的豎向振動為加勁梁第二階反對稱豎彎振動。

（3）主纜振動形態：顫振臨界狀態時，主纜的豎向振動幅值遠大于加勁梁，說明對于特大跨度懸索橋，主纜的振動幅值很大，需要引起注意。另外，主纜沿橋梁軸向振動的幅值也較大。

3 二維和三維顫振分析結果的解釋

通過對特大跨度懸索橋二維和三維顫振分析的對比研究，不難發現無論從顫振臨界風速還是顫振頻率來看，5000m特大跨度懸索橋的二維和三維顫振分析結果相差均較小，有較大程度的可比性，這有悖于人們對于特大跨度懸索橋的傳統認識。這種現象可以從以下幾個角度來解釋：

（1）三維顫振臨界狀態時，加勁梁的顫振形態是以扭轉為主的耦合顫振，豎彎振動在顫振運動中有較大程度的參與，加勁梁的側向振動模態雖然也參與了顫振運動，但是參與程度較小，不是導致顫振發散的主要模態。而二維顫振臨界狀態時，也是以加勁梁的扭轉為主的耦合顫振，豎向自由度參與較為強烈。從這點來看，兩者是統一的，只不過對于三維顫振分析，還有其它高階模態參與進來，高階模態的參與會有正負效應，可能會升高或者降低顫振臨界風速值。

（2）三維顫振分析時，計入了纜索系統的荷載，包括自激力和靜風荷載，且考慮了這些荷載沿著高度的梯度變化。計入纜索系統的風荷載相當于增加了系統的氣動阻尼，可以提高顫振臨界風速和降低顫振頻率，據已有文獻記載，江陰大橋顫振臨界風速可以提高0.8%。

（3）三維顫振分析時，考慮了纜索系統的振型，這可以提高顫振臨界風速，索橫弦向位移的參與，減小了顫振振型中主梁扭轉位移的比重，使橋梁吸收氣動阻尼的能力增加，而吸收氣動負阻尼的能力降低。這種因素導致懸索橋顫振臨界風速提高，但是效果不明顯。

（4）三維顫振分析時，考慮了側向導數的影響，雖然只是按照擬靜力理論來擬合的側向氣動導數，但在一定程度上反映了側向導數對特大跨度懸索橋顫振性能的影響。有研究表明［16－17］，側向導數對某些加勁梁斷面的懸索橋有較大的影響。而在二維顫振分析中，沒有考慮側向導數的這種影響，這導致了二維和三維顫振分析結果的差異。

4 動力和靜力穩定性能的關系

三維靜風穩定性能分析主要考慮氣動力非線性、結構幾何非線性和材料非線性。隨風速的增大，懸索橋自身風荷載呈非線性增長，懸索橋整體剛度不斷發生變化；而當風速不變時，由于振動姿態（風迎角、迎風面積）的變化，導致結構構件的靜風力、力矩、位移等沿橋梁軸線不均勻分布，也會導致結構的風荷載和剛度發生變化，帶來風荷載的非線性變化，即氣動力的非線性效應。幾何非線性表示結構有大變形發生，荷載和位移不服從線性關系，剛度矩陣在求解過程中不斷發生變化，不是固定的。懸索橋具有明顯的幾何非線性特征：首先懸索橋的主纜為幾何可變體系，主要依靠自重和加勁梁恒載獲得結構剛度以抵抗變形，纜索受力狀態表現出明顯的幾何非線性性質；其次懸索橋的加勁梁相對纖細和輕柔，結構在外荷載的作用下較易產生大變形，整體平衡方程不是基于初始平衡位置建立，而是應基于變形后的位置建立；長大的懸索橋主纜同時具有垂度效應，這也帶來了懸索橋的幾何非線性。隨著懸索橋跨度的不斷增加，其幾何非線性效應必將越來越顯著。材料非線性就是材料的本構關系不是線性的，按照鋼材的理想彈塑性曲線進行計算輸入。按照桿系結構的空間穩定理論，懸索橋結構靜力失穩的問題可以表述為下述三重非線性（幾何、材料和風荷載）方程［18］：

其中：

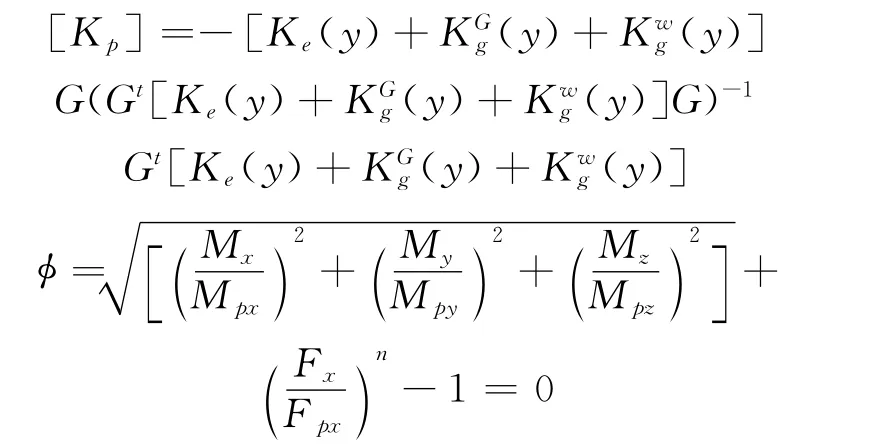
［Ke］為結構彈性剛度矩陣；［］為重力引起的結構幾何剛度矩陣；［］為風荷載引起的結構附加幾何剛度矩陣；［Kp］為結構塑性剛度矩陣；G為結構屈服面上的梯度矩陣；Mi為屈服面上的彎矩；Fi為軸向塑性力。

為研究5000m超大跨度懸索橋方案的靜風穩定性能，對兩種加勁梁方案的懸索橋分別進行了矢跨比為1∶8、1∶9、1∶10、1∶11的三維三重非線性靜風穩定全過程仿真模擬。計算獲得的靜風失穩臨界風速如圖4所示，并與三維顫振分析獲得的顫振臨界風速相互對比，研究發現：5000m特大跨度懸索橋的顫振臨界風速小于靜風失穩臨界風速，空氣動力失穩是控制設計的關鍵因素；對于寬槽加勁梁方案，靜力扭轉發散臨界風速與顫振失穩臨界風速大小相當，在同一量級上，對空氣動力失穩與靜力失穩的極限分析應置于同等重要的位置。

圖4 顫振與靜風失穩臨界風速的對比Fig.4 Comparison of critical flutter wind speed with aero static stability critical wind speed

5 結 論

從三維顫振穩定性和三維三重非線性靜風穩定性的角度，對5000m特大跨度懸索橋的空氣動力穩定性能進行了仔細研究，得出如下結論：

（1）開槽加勁梁方案的最低顫振臨界風速大于60m／s，最高達到74m／s；靜風失穩臨界風速大于120m／s，顫振發散先于靜風失穩出現；顫振和靜風失穩臨界風速都隨著矢跨比的減小有所升高；

（2）寬開槽加勁梁方案的最低顫振臨界風速大于80m／s，最高達到89m／s，靜風失穩臨界風速最低為83m／s，最高為94m／s。顫振發散和靜風失穩在相同的風速數量級出現，顫振失穩臨界風速略大于靜風失穩臨界風速；顫振和靜風失穩臨界風速都隨著矢跨比的減小有所升高；

（3）從顫振穩定性能的角度看，寬開槽加勁梁斷面優于窄開槽加勁梁方案。但是從靜風穩定性能的角度看，寬開槽加勁梁斷面次于窄開槽加勁梁方案，綜合考慮，寬開槽加勁梁方案在5000m特大跨度懸索橋的設計中優于窄開槽加勁梁斷面；

（4）從三維空氣動力穩定性能的角度證明：寬開槽和窄開槽加勁梁方案能給跨度達5000m的懸索橋提供足夠高的顫振失穩與扭轉發散臨界風速，并能滿足世界上絕大多數臺風區的要求。

［1］ AGAR T.Aerodynamic flutter analysis of suspension bridges by a modal technique［J］.Engineering Structures，1989，11（2）：75－82.

［2］ BEITH J.A practical engineering method for the flutter analysis of long span bridges［J］.Journal of Wind Engineering and Industrial Aerodynamics，1998，77：357－366.

［3］ NAMINI A，ALBRECHT P，BOSCH H.Finite element－based flutter analysis of cable－suspended bridges［J］.Journal of Structural Engineering，1992，118（6）：1509－1526.

［4］ CHEN Z.The three dimensional analysis and behaviors investigation on the critical flutter state of bridges，1994.

［5］ JAIN A，JONES N，SCANLAN R.Coupled flutter and buffeting analysis of long－span bridges［J］.Journal of Structural Engineering，1996，122（7）：716－725.

［6］ MIYATA T，YAMADA H，KAZAMA K.On a application of the direct flutter FEM analysis for long－span bridges，1995.

［7］ MIYATA T，YAMADA H，KAZAMA K.Discussion on aeroelastic detail and control in the flutter occurrences of long－span bridges［J］.Journal of Wind Engineering and Industrial Aerodynamics，1997，69：839－849.

［8］ DUNG N.Flutter responses in long span bridges with wind induced displacement by the mode tracing method［J］.Journal of Wind Engineering and Industrial Aerodynamics，1998，77：367－379.

［9］ XIANG H，GE Y.Refinements on aerodynamic stability analysis of super long－span bridges［J］.Journal of Wind Engineering and Industrial Aerodynamics，2002，90（12－15）：1493－1515.

［10］HUA X，CHEN Z.Full－order and multimode flutter analysis using ANSYS［J］.Finite Elements in Analysis and Design，2008，44（9－10）：537－551.

［11］DING Q，CHEN A，XIANG H.Coupled flutter analysis of long－span bridges by multimode and full－order approaches［J］.Journal of Wind Engineering and Industrial Aerodynamics，2002，90（12－15）：1981－1993.

［12］ZHANG X，XIANG H，SUN B.Nonlinear aerostatic and aerodynamic analysis of long－span suspension bridges considering wind－structure interactions［J］.Journal of Wind Engineering and Industrial Aerodynamics，2002，90（9）：1065－1080.

［13］CHEN A，HE X，XIANG H.Identification of 18flutter derivatives of bridge decks［J］.Journal of Wind Engineering and Industrial Aerodynamics，2002，90（12－15）：2007－2022.

［14］CHEN X，MATSUMOTO M，KAREEM A.Aerodynamic coupling effects on flutter and buffeting of bridges［J］.Journal of Engineering Mechanics，2000，126：17.

［15］ZHANG X，SUN B，PENG W.Study on flutter characteristics of cable－supported bridges［J］.Journal of Wind Engineering and Industrial Aerodynamics，2003，91（6）：841－854.

［16］MIYATA T，TADA K，SATO H，et al.New findings of coupled flutter in full model wind tunnel tests on the Akashi Kaikyo Bridge［C］.Proceeding of the Symposium on Cable－Stayed and Suspension Bridges，Deauville，France，1994：163－170.

［17］YASUI H，MARUKAWA H，GATAGIRI J，et al.Study of wind－induced response of long－span structure［J］.Journal of Wind Engineering and Industrial Aerodynamics，1999，83（1－3）：277－288.

［18］BOONYAPINYO V，LAUHATANON Y，LUKKUNAPRASIT P.Nonlinear aerostatic stability analysis of suspension bridges［J］.Engineering Structures，2006，28（5）：793－803.