導引頭二軸穩(wěn)定平臺的軸角關系和簡化

吳 曄， 朱曉峰， 陳峻山

（上海無線電設備研究所，上海200090）

0 引言

采用俯仰和偏航二軸框架結構的穩(wěn)定平臺，具有結構簡單緊湊、兩通道相互耦合小、物理含義清晰、信息處理簡單等優(yōu)點，廣泛應用于紅外、激光、雷達等各種體制的導引頭，滿足單點式或成像式導引頭截獲和跟蹤的需要［1］。該類穩(wěn)定平臺在結構上將俯仰框裝于偏航框上，但實際使用時卻常將俯仰和偏航分為相互獨立的通道分別設計［2］，并在工程中得到成功應用，查找文獻未見原因說明。

隨著捷聯(lián)慣導、捷聯(lián)導引頭等技術的發(fā)展以及導彈的功能和性能越來越高的要求，從事導引頭、彈體控制、導彈武器系統(tǒng)的研究人員對導引頭探測器相關的軸角關系越來越關注，用于解決導引頭交班、信息處理等問題［3-5］，因此研究傳統(tǒng)俯仰和偏航二軸穩(wěn)定平臺的各轉角關系及簡化方式，對新技術、新要求的應用具有研究參考價值。

本文基于導引頭相關坐標系，應用源于歐拉（Euler）定理的歐拉法［6］，推導了雷達導引頭俯仰和偏航二軸穩(wěn)定平臺的失調角、框架角、姿態(tài)角、視線角等角度之間的幾何關系，結合工程實際應用，提出角度間的簡化公式，將俯仰和偏航分離為相互獨立的兩個通道，并分析簡化后的引入誤差。為簡化問題分析，本文僅討論“十-十”氣動布局的導彈情況。

1 與導引頭有關的坐標系

與導引頭有關的坐標系有彈上參考坐標系Oxyz、彈體坐標系Ox1y1z1、導彈視線坐標系Oxsyszs、彈上測量坐標系Oxmymzm［7］，其中彈上參考坐標系的方向相對慣性坐標系不變，彈體坐標系用于研究彈體姿態(tài)偏航角ψ、俯仰角? 和滾動角γ，導彈視線坐標系用于研究彈上視線方位角qH和高低角qB，彈上測量坐標系用于研究導引頭天線等探測裝置的自身運動和目標探測。

彈上測量坐標系Oxmymzm建在導引頭天線上，其原點為天線旋轉中心，考慮到彈目距離遠大于彈體長度，彈體又具有足夠剛度，為討論簡單，將該坐標系原點也轉移到其它三個坐標系的原點，則在平臺零位狀態(tài)時彈上測量坐標系Oxmymzm與彈體坐標系Ox1y1z1重合。

2 平臺中軸角關系和簡化

2.1 框架角

依次轉動偏航框架角ψa 和俯仰框架角?a后，測量坐標系Oxmymzm的Oxm軸與彈體坐標系Ox1y1z1的Ox1軸的夾角為φa，如圖1所示。

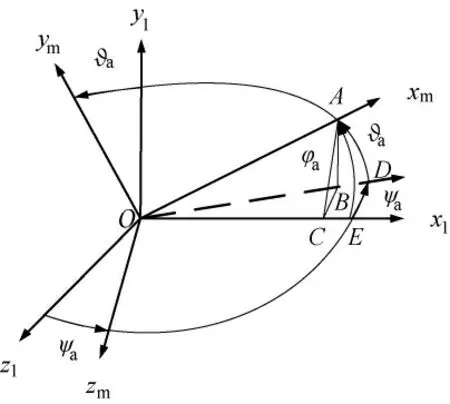
圖1 彈上測量坐標系與彈上執(zhí)行坐標系之間的關系

由AB ⊥OB，BC ⊥OC，得到OC ⊥AC，因此φa與ψa、?a的關系為

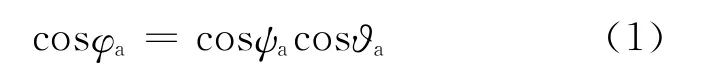
角度φa、ψa、?a均較小時，認為OA ＝1≈OB≈OC，則近似得到

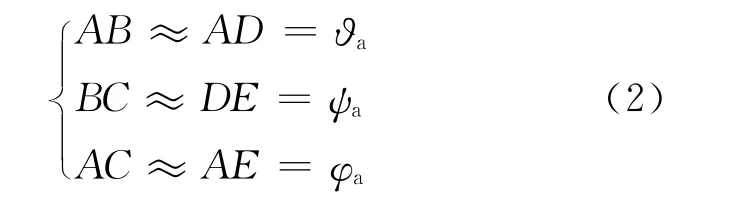
由AB2+BC2＝AC2得到

取

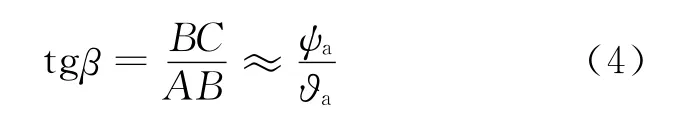
則得到簡化方式為

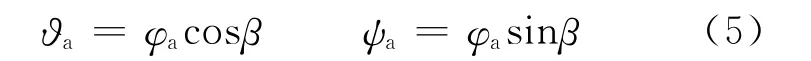
通過式（5）將圖1表示的空間幾何關系轉化為圖2表示的平面角度矢量關系，即偏航框架角ψa和俯仰框架角?a相互正交獨立，測量裝置敏感軸Oxm相對彈體坐標系Ox1軸的轉動角φa 由ψa和?a矢量相加而合成。

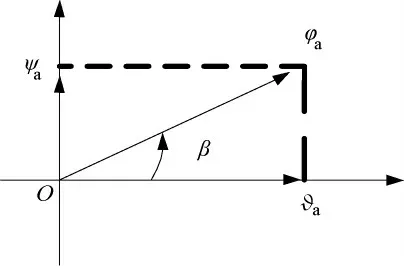
圖2 框架角的簡化平面矢量圖

2.2 角預定

角預定的目的是將導引頭天線指向預先對準目標或前置一個角度，以便目標回波信號能準確落在導引頭回波天線波束范圍內，保證導引頭截獲目標。角度預裝由彈上計算機給出角預定信號，提供給導引頭角預定回路來執(zhí)行。角預定回路是位置伺服回路，裝在穩(wěn)定平臺內外框二個執(zhí)行軸上的電位器測量框架角信號，當該信號與預定信號平衡時，預定功能完成。

當彈上計算機給出導彈視線預裝的方位角qH和高低角qB后，則預裝的視線指向Oxs軸在參考坐標系Oxyz中確定。在導彈偏航角ψ、俯仰角?和滾動角γ已知時，由參考坐標系Oxyz依次轉動偏航角、俯仰角和滾動角得到彈體坐標系Ox1y1z1，再通過穩(wěn)定平臺轉動偏航框架角ψa 和俯仰框架角?a將彈上測量坐標系Oxmymzm的Oxm軸與Oxs軸重合，完成角預定。

設導彈視線坐標系Oxsyszs中預裝的目標在Oxs軸上有單位矢量，得到該矢量在參考坐標系Oxyz 上的坐標點為

同理，當完成角預定后，該矢量落在Oxm軸上，得到該矢量在參考坐標系Oxyz 上的坐標點為

由Oxs軸上單位矢量在參考坐標系Oxyz 上的坐標點與Oxm軸上單位矢量在參考坐標系Oxyz 上的坐標點相等，計算得到偏航框架角ψa和俯仰框架角?a。導彈通常能夠獲取預裝目標在參考坐標系上的坐標（x，y，z），通過歸一化使x2+y2+z2＝1，則利用上兩式也可得到偏航框架角ψa 和俯仰框架角?a。

若無導彈姿態(tài)角的影響，即ψ＝?＝γ＝0°條件下，則由式（6）和式（7）相等得

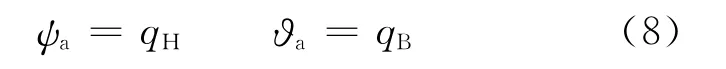
即視線預裝分別由對應通道轉動相應框架角來實現(xiàn)。

若姿態(tài)角較小，即設γ＝0°，ψ 和? 較小，則得

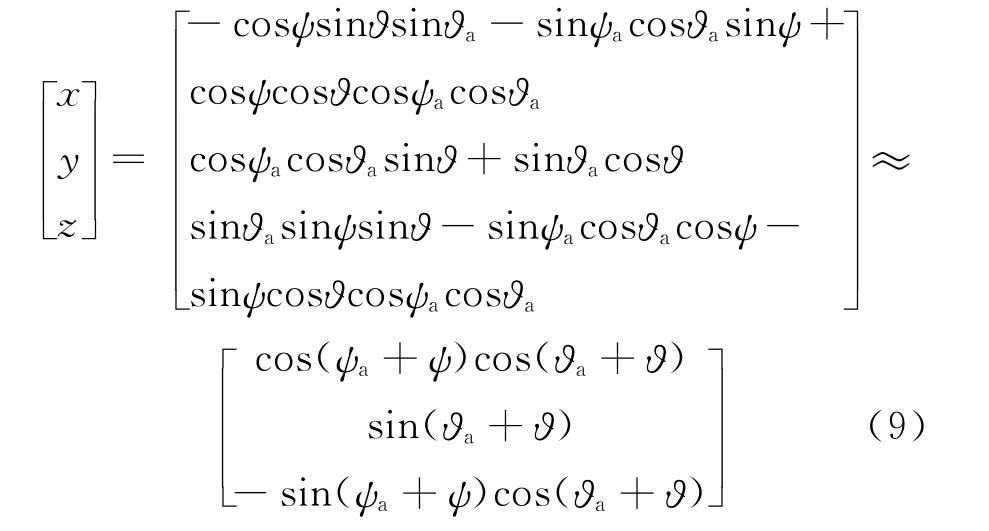
將上式與式（6）比較得到簡化公式：

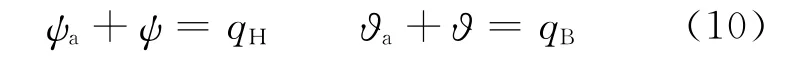
因此在彈體姿態(tài)變化時，視線預裝分別由對應通道轉動相應框架角和補償姿態(tài)角來實現(xiàn)。

2.3 視線穩(wěn)定

由式（6）可知，導彈視線坐標系Oxsyszs由參考坐標系旋轉導彈視線方位角qH和高低角qB得到。當導引頭跟蹤目標時，彈上測量坐標系Oxmymzm的Oxm軸與Oxs軸重合，為隔離彈體姿態(tài)角對視線的影響，在彈上測量坐標系Oxmymzm的Oym軸和Ozm軸上分別安裝了偏航和俯仰速率陀螺，即兩個陀螺與天線固聯(lián)在一起。這樣，在角預定后導引頭截獲目標前，接通陀螺反饋構成穩(wěn)定回路，形成簡易穩(wěn)定平臺，使測量軸Oxm在參考坐標系內保持不變。

設穩(wěn)定回路接通時刻偏航框架角為ψa0 和俯仰框架角?a0，對應的彈體姿態(tài)角分別為偏航角ψ0、俯仰角?0和滾動角γ0，則彈上測量坐標系Oxmymzm在天線指向上單位矢量在參考坐標系Oxyz 的值為

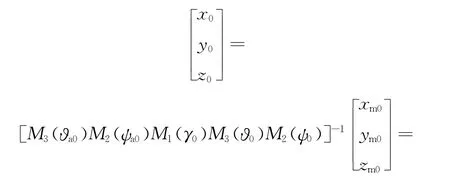
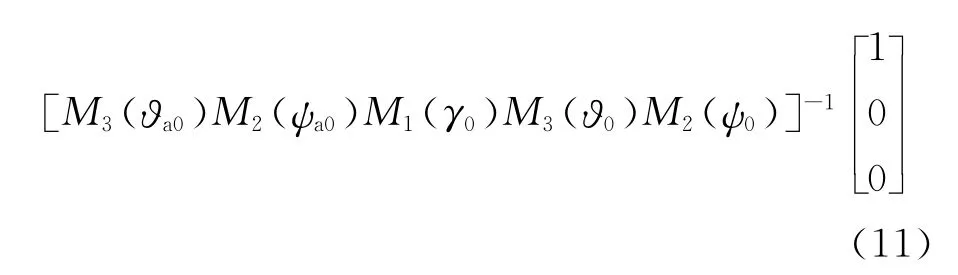
當彈體坐標系Ox1y1z1變化時，彈體姿態(tài)角變化到偏航角ψ1、俯仰角?1和滾動角γ1，在穩(wěn)定回路的理想作用下，天線指向在參考坐標系內仍保持不變，則彈體變化使穩(wěn)定平臺偏航框架角變?yōu)棣譨1和俯仰框架角變?yōu)?a1，其值可由下列公式求得

參照式（10）處理方法，在姿態(tài)角較小時，可近似得

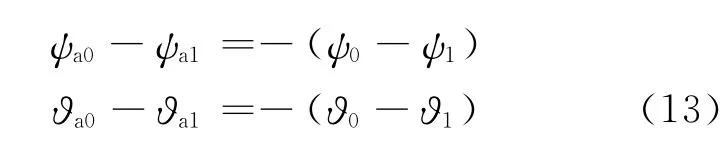
由上式看到，在穩(wěn)定回路的理想作用下，彈體姿態(tài)角的變化只引起穩(wěn)定平臺兩個通道框架角的變化，視線穩(wěn)定由兩個通道隨對應彈體姿態(tài)變化分別反轉相應框架角來實現(xiàn)。

2.4 失調角

采用單脈沖測角方式的雷達導引頭，通過天線和接收機測得視線與天線電軸失調角ε 在偏航、俯仰兩個測量通道的分量εy、εz，這兩個失調角分別是彈目標視線在彈上測量坐標系Oxmymzm兩個正交平面xmOzm和xmOym的投影與Oxm軸的夾角，如圖3所示，圖中T 為目標，φε為平面TOA 和xmOym的夾角。

由圖3得

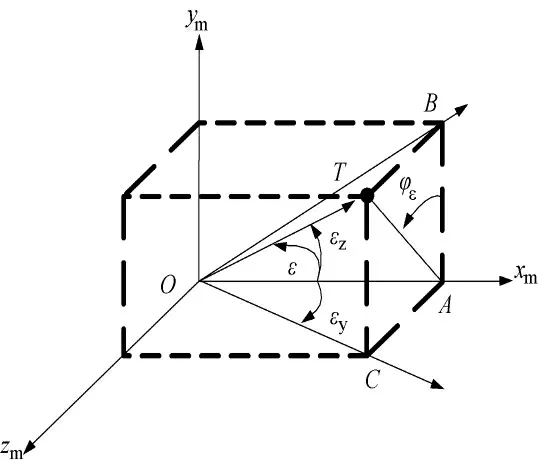
圖3 視線在彈上測量坐標系的測量值

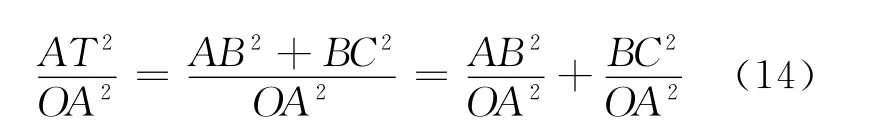
即

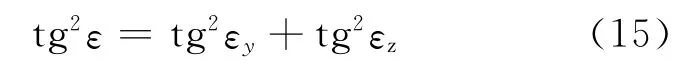
實際使用過程中，尤其在跟蹤狀態(tài)時，失調角ε、εy、εz均較小，設OT 長度為R，則OA、OB、OC長度均近似為R，即AT＝Rε，AC＝Rεy，AB＝，得

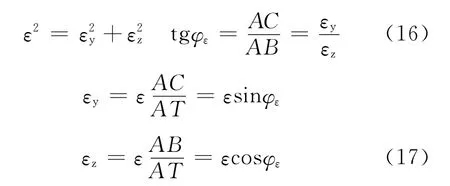
通過式（17）將圖3表示的空間幾何關系轉化為圖4表示的平面角度矢量關系，即偏航、俯仰兩個相互正交獨立測量通道的分量εy、εz合成了視線與天線電軸失調角ε。

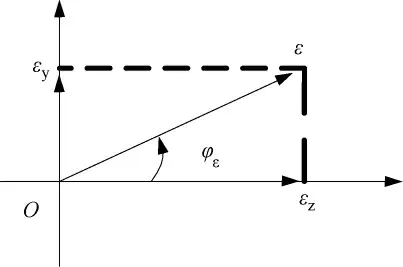
圖4 失調角的簡化平面矢量圖

2.5 角跟蹤

通過角度預裝將導引頭天線指向目標附近，此時導引頭截獲，按圖3測量得到視線與天線電軸失調角ε在偏航、俯仰兩個測量通道的分量εy、εz，這兩個分量控制穩(wěn)定回路減小失調角，試圖將彈上測量坐標系Oxmymzm的Oxm軸與視線重合，也即與導彈視線坐標系Oxsyszs的Oxs軸重合。

在無彈體姿態(tài)影響時，偏航需轉動框架角Δψa，俯仰需轉動框架角Δ?a，才可使天線電軸與視線重合，如圖5所示。

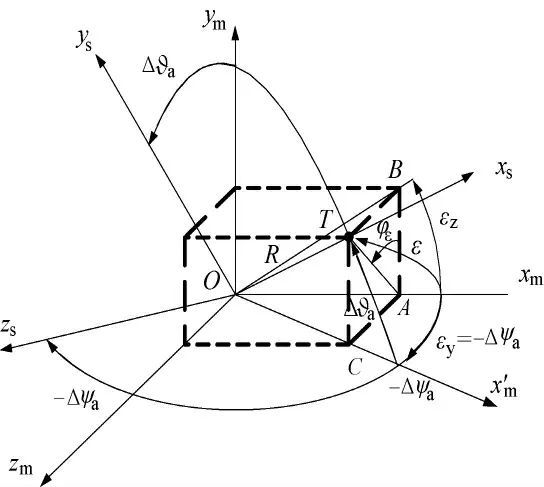
圖5 失調角與框架角的關系

由圖得到

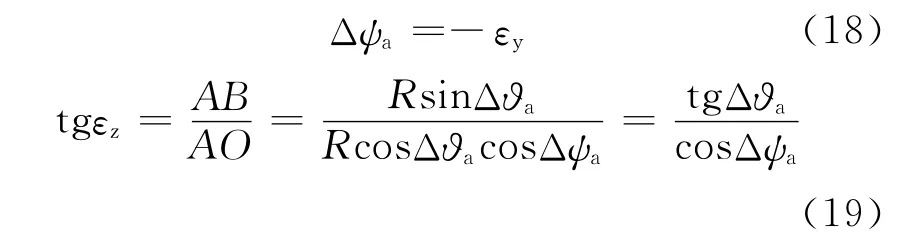
在跟蹤狀態(tài)時失調角εy較小，由cosεy＝cosΔψa ≈1，得

由式（18）和式（20）可知，在無彈體姿態(tài)影響時，測得偏航、俯仰各自失調角分量分別轉動對應通道的框架角即可實現(xiàn)角跟蹤。存在彈體姿態(tài)變化時，則還需按式（13）由穩(wěn)定回路轉動相應框架角來消除彈體姿態(tài)的影響。

2.6 各軸角間的簡化關系

按照框架角、角度預裝、視線穩(wěn)定、失調角和角跟蹤中提到的軸角關系，采用簡化公式后，可以將俯仰和偏航兩個正交通道相互獨立開來。以俯仰通道為例按單通道工作整理各軸角關系，并簡化符號為失調角ε、框架角φ、姿態(tài)角?、視線角q。參照角度預裝的分析方式，可以得到天線電軸相對參考坐標系轉角θ的簡化關系為

再參照角跟蹤分析，可以得到

得到俯仰通道各軸角的一維簡化關系圖如圖6所示，將帶正余弦的復雜關系簡化為線性關系。

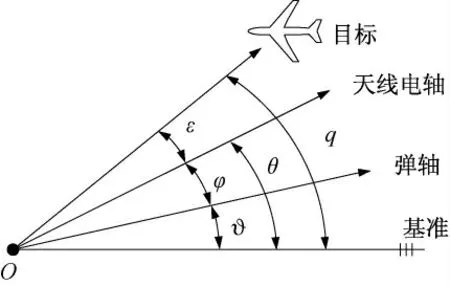
圖6 導引頭角度關系簡化示意圖

圖中基準為參考坐標系的Ox 軸，彈軸為彈體坐標系的Ox1軸，天線電軸為彈上測量坐標系的Oxm軸，目標為導彈視線坐標系的Oxs軸。

3 簡化引入的誤差

3.1 框架角簡化的誤差

由式（5）選取不同的φa，隨著β（0°～90°）變化，精確式（1）與簡化式（3）得到的合成角誤差曲線如圖7所示。

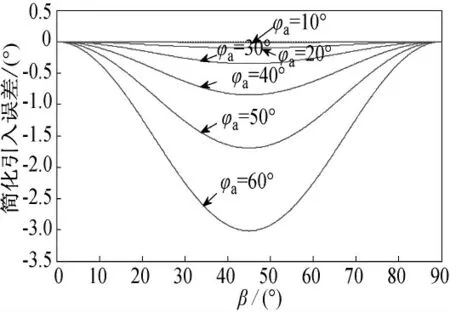
圖7 框架角簡化公式的誤差曲線

由圖看到，φa 越大簡化公式的誤差越大；φa 不變則β＝45°時，ψa ＝?a，簡化公式的誤差最大；φa＝60°時簡化公式的誤差最大為3°。由于結構空間的限制，俯仰和偏航二軸穩(wěn)定平臺的框架角很難突破±60°，因此采用簡化式（5）引入的誤差不會大于3°。在實際進行角預定時，彈上計算機應根據(jù)具體指標要求并結合式（10）來確定視線預裝角。

3.2 失調角簡化的誤差

由式（17）選取不同的ε，隨著β（0°～90°）變化，精確式（15）與簡化式（16）得到的合成角誤差曲線如圖8所示。

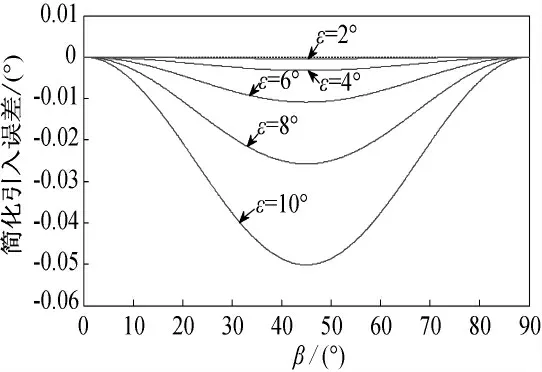
圖8 失調角簡化公式的誤差曲線

由圖看到，ε越大簡化公式的誤差越大；ε不變則β＝45°時，εy＝εz，簡化公式的誤差最大。在實際使用中，一般ε均小于10°，簡化式（17）引入的誤差不會大于0.05°，滿足導引頭的使用要求，因此實際應用時，直接由各自通道測得的失調角分量形成視線角速度去控制彈體對應通道的舵機。

4 結束語

本文應用歐拉法推導了雷達導引頭俯仰和偏航二軸穩(wěn)定平臺中各角度之間的關系，為導引頭天線位置控制提供了依據(jù)，在此基礎上應用方向余弦法、四元數(shù)法等無奇點算法，可開展更深入、更廣泛的研究工作，對于捷聯(lián)導引頭的信息處理也有一定的參考價值。在誤差允許的條件下，采用簡化公式可以將俯仰和偏航兩個通道相互分離，簡化了二軸穩(wěn)定平臺的分析研究，使實際工程應用更方便。

［1］ 穆學楨，周樹平，趙桂瑾.AIM-9X 空空導彈位標器新技術分析和評價［J］.紅外與激光工程，2006，35（4）：392-394.

［2］ 穆虹.防空導彈雷達導引頭設計［M］.北京：宇航出版社，1996.

［3］ 趙洪亮，毛士藝，李少洪.空空導彈導引頭角預定精度研究［J］.火力與指揮控制，1999，24（1）：15-19.

［4］ 丁赤飆，毛士藝.主動尋的末制導的截獲性能分析［J］.航空學報，1997，18（4）：473-476.

［5］ 李秋生.相控陣雷達導引頭捷聯(lián)去耦技術研究［J］.制導與引信，2005，26（2）：19-22.

［6］ 董秋泉，肖尚彬，蔡泰信.陀螺系統(tǒng)［M］.西安：西北工業(yè)大學，1984.

［7］ 彭冠一.防空導彈武器制導控制系統(tǒng)設計（上）［M］.北京：宇航出版社，1996.