基于線性互補理論求解絕對值方程

鄧永坤，張萍，曹蘇玉

（中國礦業大學理學院，江蘇徐州 221000）

基于線性互補理論求解絕對值方程

鄧永坤，張萍，曹蘇玉

（中國礦業大學理學院，江蘇徐州 221000）

針對絕對值方程Ax-|x|=b的求解問題.在假設1不是矩陣A的特征值時，絕對值方程可轉化為線性互補問題，然后將線性互補問題轉換為非光滑方程組的形式進行求解，進而求得原絕對值方程的解.

絕對值方程；線性互補問題；非光滑方程組

1 引言

考慮以下形式的絕對值方程

其中A∈Rn×n，b∈Rn，絕對值依分量而取.

絕對值方程首次由Rohn于1989年在文獻[1]中研究區間線性方程組問題時提出，此后許多學者對其理論及數值求解進行了廣泛的研究.Mangasarian等人在文獻[2]中對絕對值方程（1）進行了詳細的理論研究，證明了當1不是矩陣A的特征值時，絕對值方程（1）可以轉換為線性互補問題，給出了方程有解、無解、唯一解、非負解及2n個解的充分條件等.文獻[3]中，Mangasarian用廣義牛頓法對絕對值方程（1）進行求解，并且證明了在適當條件下該算法具有線性收斂速度.文獻[4]用一個光滑函數代替絕對值函數后給出了求解該絕對值方程的一個光滑牛頓法，并證明了該算法具有二次收斂性.文獻[5-6]結合區間算法相關知識，給出了求解絕對值方程（1）的區間算法.文獻[7-8]基于極大熵函數光滑化處理，給出了求解絕對值方程（1）的極大熵自適應微粒群混合算法及和聲搜索算法.

當絕對值方程（1）中矩陣A是對稱矩陣時，文獻[9]結合優化技術給出了求該絕對值方程的一種迭代算法，緊接著文獻[10]利用一種改進的Gauss-Seidel算法對其進行了求解，并且文章最后理論分析與數值實驗均證明了此算法計算速度要明顯快于文獻[9]中的迭代算法.

目前絕對值方程的現有算法多是基于半光滑或光滑化處理技術下的有效算法，在計算過程中分別利用了絕對值方程的廣義梯度及近似逼近.然而很少有文章通過將絕對值方程等價轉化為其他相關問題進行求解，本文正是基于這一點同文獻[11]的基本思想一致，首先將絕對值方程（1）等價轉化為線性互補問題，然后利用互補理論的相關知識來求解.現階段線性互補理論與算法已經十分成熟，由此可見此方法對于求解絕對值方程問題是十分有效的.

2 等價性轉化

定義2.1[12]設M∈Rn×n是一n×n實矩陣，q∈Rn是一n維矢量，F:Rn→Rn為連續可微的向量值函數，且F=Mx+q，則線性互補問題（linear complementarity problems）記為LCP（F），是指：求x∈Rn滿足

即xi≥0，Fi(x)≥0，xiFi(x)=0，i=1,2,…n.

定義2.2[12]函數ψ:R2→R1被稱為“NCP函數”，如果對任意(a,b)T∈R2，ψ(a,b)=0當且僅當a≥0，b≥0，ab=0.

從事優化理論與算法研究的學者提出了許多不同的NCP函數，其中較為常用的有以下兩個NCP函數：

1.Fischer-Burmeister函數：

2.min函數：

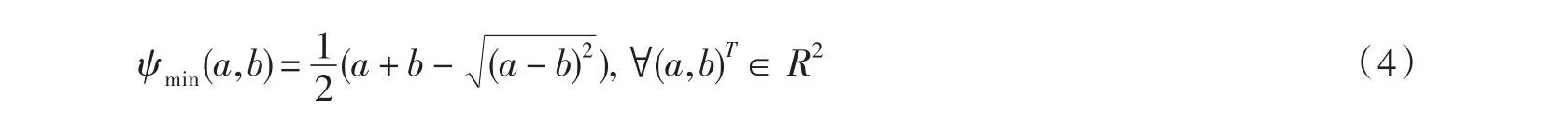
由定義2.1[12]及定義2.2[12]可知，對于任意的NCP函數ψ，LCP（F）可等價地轉化為方程組：

引理[2]假設1不是矩陣A的特征值，則絕對值方程Ax-|| x=b可等價轉化為以下線性互補問題

其中：M=(A+I)(A-I)-1，z=(A-I)x-b，q=((A+I)(A-I)-1-I)b，I為n×n的單位矩陣.

由式（5）、（6），絕對值方程（1）可以等價轉化為以下方程組：

其中：F(z)=Mz+q，M、z、q、I如引理[2]所示.

（7）式中NCP函數ψ假如取Fischer-Burmeister函數（或min函數），則絕對值方程（1）可等價轉化為以下非光滑方程組：

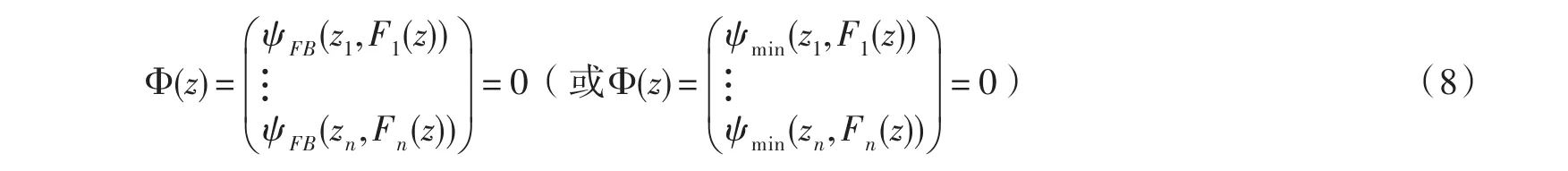
至此，絕對值方程（1）的求解問題轉化為了非光滑方程組（8）的求解問題.通過求解，非光滑方程組（8）求得解z*，再求解線性方程組z*=(A-I)x-b，求得x*即原問題絕對值方程（1）的解.

接下來構造非光滑化方法、光滑化方法及優化方法三類較為有效且常用的方法對非光滑方程組（8）進行求解.

3 算法構造

3.1 非光滑化方法

非光滑化方法的基本思想是利用基于Clarke[13]意義下的廣義Jacobian矩陣進行求解非光滑方程組（8），從而得到原互補問題及絕對值方程（1）的解.該方法始于20世紀90年代早期，隨著眾多學者對非光滑研究的不斷深入，非光滑化方法得到了迅速的發展，并成為當時最優化研究中極為活躍的領域之一.

定義3.1[14]向量值函數H:Rn→Rn在點x∈Rn局部Lipschitz連續，即存在ε＞0，L＞0使

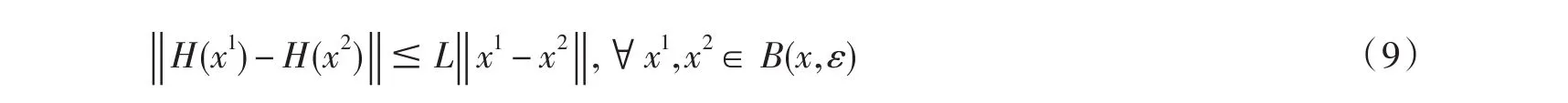
定義3.2[14]H為局部Lipschitz函數，稱矩陣集

為H在x的B-次微分.稱B-次微分的凸包為H在x的Clarke[13]意義下的廣義Jacobian矩陣集，記為

基于Clarke[13]意義下的廣義Jacobian矩陣集（11），非光滑方程組（8）可以利用文獻[12]中De Luca，Fac?chinei和Kanzow[15]給出的半光滑牛頓法求解，并且該算法具有大范圍和局部收斂性質；也可以利用文獻[12]中給出的Yamashita-Fukushima算法進行求解，該算法搜索方向僅需求解一次擾動Newton方程即可，進一步減小了計算量.

在絕對值方程問題的求解中，文獻[3]基于廣義的Jacobian矩陣給出了求解絕對值方程（1）的廣義牛頓法；文獻[16]利用廣義的Jacobian矩陣及廣義牛頓法求解了絕對值方程（1）的一種廣義形式Ax+B|x|=b，并且證明了該方程與二階錐互補問題的等價性，進而延伸到求解二階錐互補問題.可見非光滑化方法對于求解絕對值方程是十分有效的方法之一.

3.2 光滑化方法

光滑化方法的基本思想是對非光滑方程引進光滑逼近方程，然后利用光滑化方法求解光滑逼近方程，進而求得原非光滑方程的解.

定義3.3[12（光滑逼近函數）給定函數H:Rn→Rn，稱光滑函數Hμ(·):Rn→Rn（μ＞0）為H的光滑逼近函數，如果對任意的x∈Rn，存在κ＞0，使得

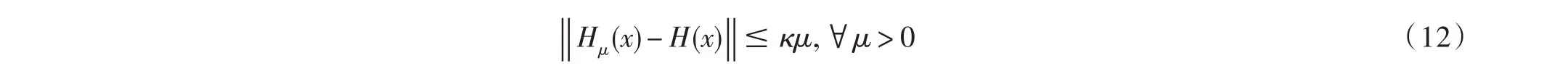
如果κ不依賴于x，則稱Hμ(·)為H的一致光滑逼近函數.

為求解非光滑方程組（8），文獻[12]引進以下光滑函數：

1.Fischer-Burmeister函數的光滑函數：

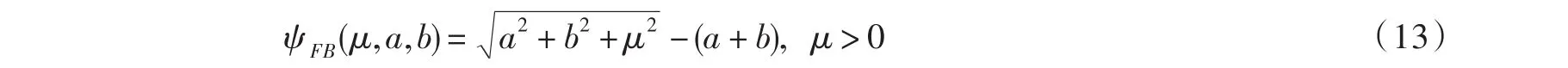
2.min函數的光滑函數：

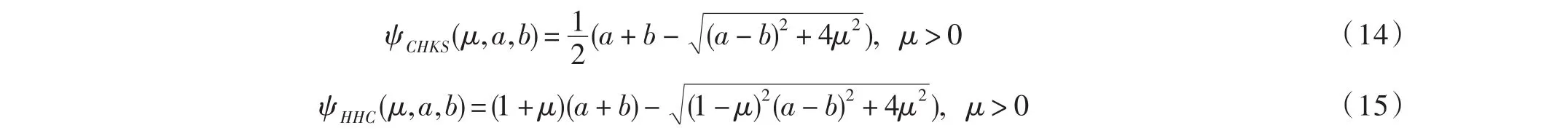
由光滑函數（13）、（14）、（15）可以得到非光滑方程組（8）的光滑逼近方程組：

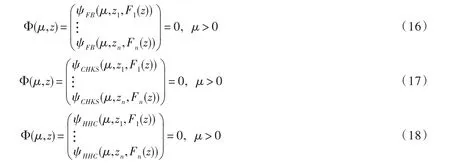
至此，我們通過引進光滑函數構造光滑逼近方程將非光滑方程組（8）進行了光滑化處理，得到對應的光滑逼近方程組（16）、（17）、（18），然后就可以利用光滑函數的相關算法來求解（16）、（17）、（18），進而求得非光滑方程組（8）即絕對值方程（1）的解.

在絕對值方程問題的求解中，文獻[11]利用了ψCHKS(μ,a,b)光滑化函數進行光滑逼近，然后利用非內部連續化算法進行求解取得了較好的研究成果，可見該光滑化方法對于求解絕對值方程問題也是十分有效的.此外還有許多學者的研究文獻[4-5，7-8，17]直接對非光滑的絕對值|| x進行了光滑化處理，然后進行相關求解，也取得了非常好的成果.

3.3 優化方法

優化方法的基本思想是基于第一部分中絕對值方程（1）等價轉化為非光滑方程組（8），然后將非光滑方程組（8）進一步轉化為無約束優化問題，接著用無約束優化類方法對其進行求解，進而求得絕對值方程（1）的解.

非光滑方程組（8）可轉化為求解以下無約束優化問題的全局最優解：

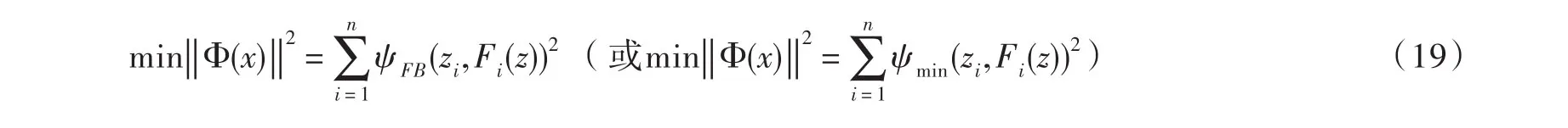
且此無約束優化問題的最優值為零.

現階段對無約束優化理論及其算法的研究工作已經十分成熟，基于這一點，將絕對值方程（1）通過一系列轉化為無約束優化問題（19）進行求解不失為一種十分有效的計算方法.

4 結束語

本文基于線性互補理論利用兩種不同的NCP函數（Fischer-Burmeister函數或m in函數）將絕對值方程（1）等價轉化為非光滑方程組，然后構造了求解該非光滑方程組的非光滑化方法、光滑化方法及優化方法，該三類方法也是大家較為熟知且常用的方法，不僅算法復雜度相當而且均可以間接求得絕對值方程（1）的解，可否利用其他更好的等價性理論對絕對值方程進行等價性轉化及求解將是我們下一步要做的主要工作.

[1]Rohn J.Systems of linear intervalequations[J].Linear A lgebra and Its Application,1989,126(11):39-78.

[2]Mangasarian O L,Meyer R R.Absolute value equations[J].Linear Algebra and Its Application,2006,419(5):359-367.

[3]Mangasarian O L.A generalized Newtonmethod for absolute value equations[J].Optimization Letters,2009,3(1):101-108.

[4]Caccetta L,Qu B,Zhou G L.A globally and quadratically convergentmethod for absolute value equations[J].Computation Optim iza?tion Application,2011,48(1):45-58.

[5]王愛祥，王海軍.絕對值方程的區間算法[J].貴州大學學報，2010，27（2）：7-10.

[6]Wang A X,Wang H J,Deng Y K.Interval algorithm for absolute value equations[J].Central European JournalMathematics,2011,9 (5):1171-1184.

[7]雍龍泉，孫培民，高凱.極大熵自適應微粒子群混合算法求解絕對值方程[J].計算機應用研究，2011，28（7）：2479-2481.

[8]雍龍泉.基于凝聚函數的和聲搜索算法求解絕對值方程[J].計算機應用研究，2011，28（8）：2922-2926.

[9]Noor M A,Iqbal J,Al-Said E.On an iterative method for solving absolute value equations[J].Optimization Letters,2012,6(5): 1027-1033.

[10]NoorM A,Iqbal J,KhattriS,etal.A new iterativemethod for solving absolute value equations[J].International Journalof the Phys?ical Sciences,2011,6(7):1793-1797.

[11]封京梅.求解一類絕對值方程組的非內部連續化算法[J].陜西科技大學學報，2011，29（2）：165-169.

[12]韓繼業，修乃華，戚厚鐸.非線性互補理論與算法[M].上海：上海科學技術出版社，2006.

[13]Clarke FH.Optimization and Nonsmooth Analysis[M].Philadelphia:SIAM,1990.

[14]白梅花，翟麗麗，章樹玲，等.非線性互補問題轉化為無約束優化問題的方法[J].陰山學刊，2008，22（2）：5-7.

[15]De Luca T,Facchinei F,Kanzow C.A semismooth equation approach to the solution of nonlinear complementarity problems[J].Math Programming,1996,75:407.

[16]Hu S L,Huang Z H,Zhang Q.A generalized Newton method for absolute value equations associated with second order cones[J]. ComputationalOptimization and Applications,2011,235:1490-1501.

[17]鄧永坤，張萍.絕對值方程的光滑牛頓算法[J].黑龍江科技學院學報，2011，26（6）：499-502.

Solving Absolute Value Equations Based on Linear Complementarity Theory

DENG Yong-kun,ZHANG Ping,CAO Su-yu
(School of Sciences,China University of Mining and Technology,Xuzhou 221000,China)

Aimed at the solution to the absolute value equations,the absolute value equations can be transformed into linear complementarity problems under the condition that one is not an eigenvalue of,and then the linear complementarity problems can be reformulated as a nonsmooth system of equations.The authors of this paper find the solution to absolute value equations by solving the nonsmooth system of equations.

absolute value equation;linear complementarity problems;nonsmooth system of equations

O24

A

1008-2794（2012）08-0008-05

2012-07-07

鄧永坤（1988—），男，山東青州人，中國礦業大學理學院2010級碩士研究生，研究方向：計算數學.