用文字概率衡量不確定性:特征和問題

杜雪蕾 許潔虹 蘇寅 李紓

摘要文字概率是衡量不確定性的方式之一，即人們使用諸如“也許”、“未必”的詞匯來描述特定事件發生的可能性。文字概率不同于數字概率，主要體現在文字概率的模糊性、非概率運算性和語義特性上。這使得相對于數字概率，用文字概率衡量不確定性既有優勢也有問題，進而對人們的不確定信息溝通和風險決策造成影響。雖然文字概率與數字概率存在特征上的差異并且人們在日常交流中偏愛文字概率，但是大部分風險領域的研究卻僅局限于數字概率，今后有必要研究使用文字概率測量的風險決策。在已有文字概率特征研究的基礎上，還可以進一步探究其不同于數字概率的其它特征(文字／數字概率與雙系統模型的聯系、文字概率的跨文化差異等)及其對風險決策的影響。

關鍵詞文字概率；數字概率：模糊性；非概率運算性；語義特性

分類號B849：C93

我們生活在一個不確定的世界之中，“天有不測風云，人有旦夕禍福”，為求生存幾乎每天都需要接收和傳達各種不確定的信息，比如“明天的天氣如何”、“未來股票走勢如何”等等。這些關于未來的不確定信息構成了我們制定計劃、做出決策的基礎，有時甚至是“唯一的救命稻草”。人們在表征不確定信息時通常使用概率形式，即為不確定事件的每個結果附加一個“可能性”的描述，例如“明天很有可能下雨”。“很有可能”是衡量概率的一種文字形式，屬于文字概率(verbal probability／linguistic probability／probability phrase)；另外一種常見的表達概率的形式是數字概率(numericalprobability)，如40％，60％-80％等。

風險決策領域的研究者們比較偏愛使用數字概率，因為數字概率客觀易量化；但是調查卻發現人們在日常交流中比較偏愛使用文字概率，因為文字概率自然易理解(Budescu，Weinberg，&Wallsten，1988)。這種差異使研究者們意識到，要了鰓人們不確定信息溝通和風險決策的過程，還需要對文字概率進行研究。因此，有研究者們開始關心文字概率在不確定信息溝通和風險決策中的作用及其與數字概率的差異，試圖回答這樣兩個問題：“文字概率是否能更有效地溝通不確定信息?文字概率是否能引導人們在風險情境下做出更有利的決策?”于是，一系列的研究開始聚焦于文字概率和數字概率的特征比較，探索它們對推理和決策等認知過程的不同影響(Budescuet al.，1988，)，或者它們在諸如會計、醫療、氣象預報等實際應用領域中的不同效用(Handmer&Proudley,2007；Juanchich，Teigen，&Villejoubert，2010；Welkenhuysen，Evers-Kiebooms，&d''Ydewalle，2001)。分析前人的研究結果可以發現，對于上述兩個問題的回答沒有一個簡單明確的答案。也許這并不是一個“好或壞”的問題，而是一個“好在哪里與壞在哪里”問題。用文字概率衡量不確定信息有其獨有的特征，既能為人們的不確定信息溝通和風險決策帶來益處，也能帶來困擾和問題。

雖然同為衡量不確定性的方式，文字概率和數字概率卻溯源于不同的系統，前者主要隸屬于語言體系，后者則發展自數學體系。這種背景差異導致文字概率相對于數字概率在表達不確定性時表現出獨特的特征，了解這些特征有助于回答文字概率“好在哪里與壞在哪里”的問題，也可以幫助研究者深入理解人們在日常交流中偏愛文字概率的原因(不僅是自然易理解)，還可以發現目前使用數字概率表征風險的實證研究對人們風險決策中某些特點的忽視。因此本文沒有對關于文字概率的所有研究進行總結評論，而是重點關注文字概率衡量不確定性時的特征和問題，主要針對文字概率和數字概率的區別展開評述，總結討論相對于數字概率，文字概率具有哪些特征，以及這些特征會對人們的不確定信息溝通和風險決策發揮哪些優勢和帶來哪些問題。同時，在總結文字概率的特征和問題的基礎上，本文將探討文字概率可能存在的其它區別于數字概率的特征，并對未來的研究進行方向性的展望。

1文字概率的模糊性

文字概率的模糊性(vagueness)最初是由Wallsten等人(1986)提出的，主要指相對于數字概率而言，文字概率所代表的不確定性水平具有更大的跨度，而且這種跨度沒有明確的界限，從而在解釋文字概率時，其意義具有更大的被試間和被試內變異，也就是說文字概率的意義會因被試不同、時間不同、情境不同而發生變化。需要注意的是，Budescu等(1988)認為模糊性的意思不同于模棱兩可(ambiguity)。后者指某種事物能夠被理解成兩種或兩種以上的意義，但是每種意思都是精確(precise)的，而前者是指某種事物的意義不能夠被精確(imprecise)地定義或者理解。

文字概率的模糊性是相對于數字概率的精確性而言的，所以考察模糊性的最直觀方式就是將文字概率映射到數字概率的標尺上，測查其代表的數字概率范圍大小和因外界條件變化而產生的各種變異。這種研究視角最早得到研究者的認可和關注，一批早期研究文字概率的實驗也通過這種“文字概率的數字轉換”范式發現了文字概率的一些不同于數字概率的特性(Clark，1990；Clarke，Ruffin，Hill，&Beamen，1992；Mosteller＆Youtz，1990；Reagan，Mosteller,&Youtz，1989；Wallsten etal.,1986)。在這些早期研究中，Wallsten等人對文字概率的模糊性進行了比較系統的測量，并且提出了文字概率的代表性函數(membershipfunction)。因此本部分主要對代表性函數所體現出來的模糊性進行詳細的介紹，然后再評述一下文字概率模糊性在不確定信息溝通中的作用以及由此帶來的問題。

1.1模糊性的體現：代表性函數(membership function)

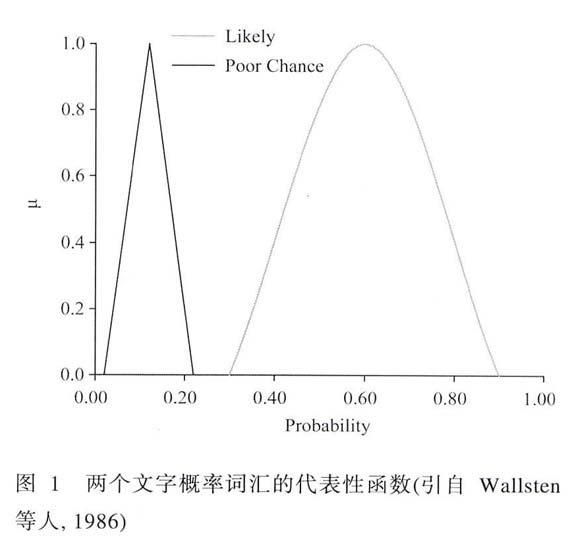
1986年，Wallsten等人利用成對比較方法(apair-comparison method)構建出文字概率的代表性函數，用以表征文字概率在轉換成數字概率時其意義的模糊性。所謂的代表性函數如圖1所示。每一個文字概率詞都有自己的代表性函數，橫軸表示相應的數字概率，定義域為[0.0，1.0]中的一段；縱軸表示某個數字概率(如50％)能夠被該文字概率詞表征的程度，取值為[0.0，1.0]，0.0指該文字概率完全不能被解釋成某數字概率值，1.0指該文字概率絕對能夠被解釋成某數字概率值。代表性函數表明當將文字概率映射到數字概率的標尺上時，其代表的是一段數字概率區間，并且區間中不同數字概率的代表程度不同。

通過對大部分文字概率的代表性函數的觀察和分析，Wallsten等人(1986),總結出文字概率模糊性的三種表現水平。首先是個體水平上，在他們的實驗結果中，除“toss-up”(擲硬幣，表示勝負各半)和“doubtful”，其他文字概率詞匯的代表性函數均存在非常大的個體差異。即對于同樣的文字概率詞匯，不同的被試具有不同的代表性函數，這種不同不僅表現在函數值的大小上，而且表現在函數圖像的類型上，有的是單峰函數(如圖1)，而另一些則是單調函數(monotonic function)。其次是情境水平(context level)上，同一個文字概率詞匯的代表性函數圖像會隨著所處情境的變化而發生相應改變。例如，同樣是用“likely”形容“玩足球時腳踝被扭傷了而非骨折了”的可能性和“手背上被切除的肉瘤會在三個月后重新長出來”的可能性，被試會對這兩種情境中的“likely”賦予不同的數字概率值或區間。對此的一種解釋是事件本身的基礎率(base rate)水平會影響到被試的賦值(Viiiejoubert，Almond，＆Alison，2009；Wallsten，Fillenbaum，&Cox，1986；Weber&Hilton，1990)；另一種解釋是事件本身的代表性(representativeness)對被試的文字，數值轉換發揮作用(Windschitl&Weber，1999)。但是由于基礎率和代表性經常相互聯系，基礎率大的事件通常也有很強的代表性，所以還沒有很完善的實驗設計能夠完全區分這兩種解釋。而除了基礎率和代表性，事件的嚴重性(severity，如疾病致命與否)或危險陛(dangerousness)同樣影響到被試對文字概率詞匯的數值轉換(Weber&Hilton，1990；Viilejoubert，Almond，&Alison，2009；Harris&Corner,2011)。最后是詞匯水平上，不同概率詞匯的代表性函數的圖像類型雖然有很大差異，但是卻表現出一定的規律性，靠近數字概率極值端(如0.0或1.0)的文字概率詞匯的代表性函數多為單調函數，而位于數字概率中間部分的文字概率詞匯的代表性函數多為單峰函數。這三種表現水平說明文字概率的意義具有個體差異和情境差異，同時也反映出一定的規律性。

1.2模糊性的作用和問題

文字概率的模糊性對于人們在風險溝通中表達“不確定性”具有一定的輔助作用。當人們需要傳達不確定信息的時候，有兩方面的不確定信息需要表達：一種是事件發生與否的概率(代表性函數的橫軸)，另一種是對事件發生概率的不確定性(代表性函數的縱軸)。數字概率只能表達前一種不確定信息，如“事件發生的概率是0.5-0.8”，而文字概率能夠將兩種不確定信息均包含在內。同時，由于文字概率沒有明確的解釋邊界，所表達的這兩種不確定信息可以動態變化，所以當人們面對瞬息萬變的不確定情境時，這種可變性使文字概率受到青睞。這種青睞可以從人們的概率表達偏好上體現出來。調查顯示人們在日常交流中比較偏愛使用文字概率(Budescu et a1，，1988)，除了文字概率自然易理解之外，能夠充分表達出不確定性也是偏愛的原因之一。另外，有研究發現數字概率中“50％”的使用頻率要遠遠高于文字概率中“toss-up”的使用頻率；當要求人們對事件發生的不確定性做出數字概率判斷的時候，“50-50chance”的過度使用現象非常普遍(Bmine de Bruin，Fischhoff,Millstein，&Halpern-Felsher，2000)。這都表明當使用數字概率表達不確定時，其模糊性的匱乏使得人們不得不選擇模糊性相對較強的“50％”，特別是在缺乏具體的信息支持概率大于50％或小于50％時。而使用文字概率時，則不存在這種顧慮，所以Wallsten等人認為，從某種意義上來說文字概率能使人們更誠實地表達出心理的不確定性水平，而不過分依賴"toss-up"。

雖然文字概率的模糊性有利于人們對不確定水平的全面表達，但是也會導致不少問題。首先，人們在解釋文字概率的意義時存在比較大的不一致性，因而使用文字概率傳遞不確定信息不能保證溝通雙方對概率意義的解釋是相同的。而且Piercey(2009)發現人們對自己做出的文字概率判斷的解釋會隨著行為動機(如以“符合上司的判斷偏好”為動機)和行為結果(如“被判斷事件的實際情況”)的變化而發生改變。他在實驗中要求被試扮演會計的角色以審計某公司的財務狀況，并用文字概率的形式對該公司存在財務問題的可能性做出評估，然后請被試將自己所選擇的文字概率轉換成數字概率表征的代表性函數。結果發現，當被試得知上司的審計風格傾向于“樂觀”時(不輕易做出“財務存在問題”的評估)，他們對文字概率的解釋(代表性函數)不同于當得知上司的審計風格傾向于“悲觀”時，前者的代表性函數峰值所對應的數字概率要明顯小于后者的，即前者存在財務問題的可能性更小。當被試知道了某權威部門對該公司的財務審計結果為“存在財務問題”時，他們對文字概率的解釋也會變得更接近權威部門的審計結果。這說明文字概率容易引發人們不誠實和找借口的行為表現，即為了使自己的概率判斷更接近事實或者更符合別人的預期，人們會經常改變對文字概率的意義解釋。

其次，雖然文字概率的模糊性使人們在表達風險信息時偏愛使用文字概率；但是也正是這種模糊性使人們在接收風險信息時卻更愿意接收數字概率，因為接收信息時，文字概率中兩種不確定信息的疊加以及文字概率解釋的個體和情景差異使得人們對文字概率的加工更加復雜，遠遠超過對簡單的數字概率值的加工難度。這就導致了“溝通模式偏愛悖論”(communication ModePreference Paradox，CMPP)的存在，即在傳達信息時更偏好文字概率，而在接收信息時則更偏好數字概率(Erev&Cohen，1990；Wallsten，Budescu，&Zwick，1993；許潔虹，2009)。Xu，Ye和Li(2009)發現：CMPP悖論在中國被調查者中的比例高達58.7％。即，與美國人相比，更多的中國人喜歡聽到用數字概率明確表示的有關可能性的信息，同時卻傾向于用比較模糊的文字概率方式來傳達這些信息。在“溝通模式偏愛悖論”基礎上，李紓，許潔虹，葉先寶(2011)發現了一種新的溝通悖論，即“下情上達評價悖論”(communicationPerformance Assessment Paradox，CPAP)o他們請被調查者對“下情上達”情境下的4類管理者(2類“傳聲筒型”管理者：聽取下級的文字概率信息并向上級匯報文字概率信息：聽取下級的數字概率信息并向上級匯報數字概率信息；以及2類“信息轉化型”管理者：聽取下級的文字概率信息卻向上級匯報數字概率信息；聽取下級的數字概率信息卻向上級匯報文字概率信息)進行績效評價，發現：同樣面對忠實的“傳聲筒型”管理者，被調查者認同數字概率“傳聲筒”、而不認同文字概率“傳聲筒”；同樣面對權變的“信息轉化型”管理者，被調查者認同將數字轉化成文字概率的管理者、而不認同將文字轉化成數字概率的管理者。這兩類悖論的存在表明，文字概率的模糊性給人們的不確定信息溝通帶來了問題，導致信息傳遞方和信息接收方產生了非對稱的偏愛方式，以及導致人們對使用相同信息傳遞方式(傳聲筒或信息轉化型)的管理者產生了非理性的績效評價。

2文字概率的非概率運算性

正如之前所言，數字概率發展自精細的數學體系或概率論體系，有一套強大且嚴密的公式法則作為支撐，從而數字概率可以進行各種數學運算以滿足決策分析領域的要求。所以用數字概率表達不確定信息顯得更加精確(precise／accurate)，更加具有科學信度(scientific credibility)(Lipkus，2007)。相反，文字概率發展自語言體系，僅僅是一種對心理狀態的描述，不受數學公式和概率論法則的約束，具有非概率運算性(noll probabilisticoperation)。同時，Windschitl和Wells(1 996)研究發現，數字概率傾向于引發個體的審慎推理(deliberate reasoning)和基于規則的推理(rule—based reasoning)，文字概率傾向于引發更加聯想式(associative)、直覺式(intuitive)的思維方式，這也表明人們在使用和加工文字概率時不會考慮各種概率運算法則。目前的研究發現，文字概率的非概率運算性主要表現在“框架效應”(framingeffect)和“等概率效應”(equiprobability effect)上。

2.1框架效應

框架效應指對同一問題的不同描述會導致個體的不同反應。預期理論(prospect theory)假設人們當面對兩個收益選項時傾向于風險規避而選擇確定選項，當面對兩個損失選項時傾向于風險偏愛而選擇風險選項，盡管這兩種情況下所描述的問題本質是相同的(Kahneman&Tversky,1979)。當問題的背景換成是某種疾病是否具有感染威脅時，這種框架效應可以發生反轉。即告知被試感染疾病的可能性(損失)會導致更多的人選擇采取治療或預防措施，表現出風險規避；告知被試不感染疾病的可能性(相對性的收益)會導致更多的人選擇容忍一定水平的風險(McNeil，Pauker，Sox，&Tversky，1982)。

有研究者將感染疾病與否的正反概率和文字，數字概率表達方式結合起來，探究框架效應和文字／數字概率表達的交互作用(Welkenhuysen et al.，2001)。實驗發現，只有文字概率的表達方式出現了預期方向的框架效應。當給兩組被試分別呈現使用文字概率描述的積極信息(告知被試胎兒不會遺傳某種疾病的概率)和消極信息(告知被試胎兒遺傳某種疾病的可能性)時，得到消極信息的被試比得到積極信息的被試更愿意進行針對此遺傳疾病的產前檢查。但是當給兩組被試分別呈現使用數字概率描述的積極信息和消極信息時，得到消極信息的被試和得到積極消息的被試在進行產前檢查的意愿上沒有表現出顯著差異。Welkenhuysen等人認為這是因為對于數字概率，人們很容易進行“p”和“1-p”之間的數學運算，所以即使被告知有75％的概率不發生遺傳病，人們還是很容易就轉換成有25％的概率會發生遺傳病，因此框架效應并不顯著。但是對于文字概率，告訴人們有“a high chance''(經預實驗驗證，人們將a high chance和75％等價)不發生遺傳病，人們不容易轉換成有“a moderate chance''(同樣經預實驗驗證，人們將a moderate chance和25％等價)仍然發生遺傳病，因此表現出框架效應。這也說明文字概率更反映出人們的直覺性思維，人們不會像對待數字概率那樣做各種形式的符合規則的概率運算，表現出非概率運算特性。

2.2等概率效應

古典概率論中，等可能事件的概率計算法則是受到普遍認可的。其概率模型叫做古典概型，主要特征是試驗中所有可能的結果有限(n個)，并且每個可能的結果出現概率是相同的。例如拋一枚硬幣，可能結果只有兩個——正面或反面，而且出現正面和出現反面的可能性相同，所以出現正面的概率就應該是1／2(1，n)。

當使用數字概率進行上述概率判斷時，個體會遵守等可能事件的概率計算法則，但是當使用文字概率時，被試經常會忽視這種計算法則(Windschitl&Wells，1996；Teigen，2001)。Windschitl和Wells的實驗中讓被試分別對兩種情境進行概率判斷，情境A是“盒子中裝有10張彩票，其中有一張會中獎”，請被試判斷某人抽出一張中獎的概率，情境B是“盒子中裝有1000張彩票，其中有100張會中獎”，請被試判斷某人抽出一張中獎的概率。當被試使用數字概率量表分別對情境A和B中獎的可能性做出概率判斷時，A、B情境數字概率判斷的結果基本一致；但是當被試使用文字概率量表對情境A和B中獎的可能性做出判斷時，A、B情境的結果差異較大，B情境中獎的可能性要大于A情境中獎的可能性。而且使用數字概率和使用文字概率的差異在統計水平上是顯著的。無獨有偶，Teigen的實驗中也發現這種效應，被試被告知有三個人應聘某個職位，三個人的條件差不多，然后判斷其中某個人獲得這個職位的概率，當被試使用數字概率時，大部分人的回答是33％，但是當使用文字概率時，大部分人會認為“good chance"，“not improbable"，“entirely possible”更合適，而這些詞匯在控制組被試中被轉換成50％VA&的數字概率。Teigen將文字概率的這種效應叫做等概率效應(equiprobability effect)，它違法了等概率原則(equiprobability principle)。這也證明，人們在運用文字概率進行思考的時候，更傾向于直覺性的思維，而不會局限于概率論的公式法則。

2.3非概率運算性的作用和問題

非概率運算性表明文字概率不受數學規則約束，能引發更多的聯想式和直覺式思維，這對于預測個體的偏好和行為意圖有一定的作用，特別是當人們的決策行為不是經過審慎的分析式推理而產生的時候。例如，Windschitl和Wells(1996)的研究中，他們請被試閱讀一段情境：“假設你收到一封來自某兌獎中心的信，告知你贏取了一臺電視機和一臺錄像機。你的一個經驗豐富的朋友告訴你，這樣的兌獎信息5次中3次是真的，另外2次會強迫你在領獎前先高額消費。”閱讀之后請被試用文字量表或者數字量表預測他(她)真得贏取了免費的電視機和錄像機的可能性，然后請被試估計他們為了領獎最遠愿意花費多少路程(從30，60，120，240，480英里中選擇)。理論上講，被試預測免費獲獎的可能性越大，愿意花費的路程就越遠。研究者比較了兩種概率形式對愿意行駛的最大路程的預測程度，發現文字概率比數字概率更能預測人們的行為意愿。因此，在不確定信息溝通和風險決策中，他人使用的文字概率或許能比數字概率更有效地幫助我們推斷出他人的偏好和意圖。

非概率運算性也會給人們的不確定信息溝通和風險決策帶來一定的問題。因為人們在使用文字概率時不會進行各種概率運算，這使得概率判斷和風險決策更容易受到問題框架的影響，更容易表現出各種非理性的判斷。例如，等概率效應表明，當n個相似水平的應聘者競聘某一職位時，人們傾向于使用“good chance"、“not improbable”這樣一般被解釋為50％以上的文字概率詞匯來描述某個應聘者成功的可能性。如果某個應聘者得到如此預測的文字概率，并將其解釋為50％以上(實際上，他成功的可能性只有1／n，)，這將可能引起判斷上的過分自信等一系列問題。這樣看來，似乎放棄使用文字概率表達不確定性對人們的決策行為會更有利，但是究竟是直覺性的思考對個體決策更有利還是分析性的思考能產生更好的結果，這也是一個有爭議性的問題。Hastie和Dawes(2009)認為運用概率分析(主要使用數字符號和計算原理)進行決策，能夠使人們用分布的視角審視情境，并幫助人們定義出一個包括所有可能事件的樣本空間以及理清這些集合成員的邏輯關系。這種理性分析能夠避免思維被直覺拖入一個有限的、有系統偏差的可能事件的子集。但是Dane和Pratt(2007)在分析前人關于直覺性思考的實證研究后指出，個體進行直覺決策時其所用圖式的復雜程度和領域相關程度會影響決策結果的優劣，復雜的領域相關的“專家”圖式比簡單的領域獨立的啟發式會使直覺性決策更有效；待解決問題的結構也會影響直覺性決策的效用，問題結構比較模糊時直覺性決策會更有效，如道德判斷、藝術鑒定、企業并購等問題。由此推測，當個體面臨一個結構界定模糊的任務時，若其具有該領域的“專家”圖式，使用文字概率引發直覺性思考也許會得到更有利的結果。當然，這種推測還有待實證研究予以證實。

3文字概率的語義特性

正如數字概率那樣，文字概率可以作為衡量不確定性水平的一種量化工具。不過，從本質上來說它更是一組具有言語特征的詞匯，所以文字概率能夠表達豐富的語義信息，給不確定性的表達帶來“質”上的區別。

3.1方向性(directionality)

以往在研究文字概率時，研究者會不加區分地將 “possible”和“impossible”進行一些數值轉化，或是直接研究它們與數字概率的區別。Teigen和Brun(1999，2000)認為這樣的研究忽視了文字概率的一個很重要的語義特征——方向性(directionality)。所謂的方向性是指，文字概率可以分成兩類，一類聚焦于事件發生的可能性，如“possible”、“likely”，屬于積極詞匯(positive，)；另一類聚焦于事件發生的不可能性，如“impossible”、“unlikely”，屬于消極詞匯(negative)。這種方向性與文字概率的數值大小沒有直接的聯系，比如，同樣表示概率較低的情況，既有積極詞匯"somepossibility”，又有消極詞匯“quite uncertain”(兩者轉換成數字概率均為30％左右)。

經研究證實，大部分的文字概率具有明確的方向性，典型表現為當要求被試將句子“It is somepossibility for the operation to be successful，because……”補充完整時，絕大部分都填寫積極的理由，即解釋為什么前半句中的事件會發生；而當要求被試補充完整句子“It is quite uncertain thatthe operation will be successful，because……”時，絕大部分都填寫消極的理由，即解釋為什么前半句中的事件不會發生。而對于數字概率則不是如此，數字概率的方向性更加地模糊，且會隨著概率大小、期望水平和事件性質等情境的改變而發生變化(Teigen&Brun，1995，1999，2000)。

3.2文字概率的內／外不確定性

不確定性可以分為兩種，一種是內部的不確定性，即人們自身對“事件發生與否”或“事件是否真實”的內部評定狀態，而另一種是外部的不確定性，即客觀事件本身所具有的各種可能性(Hacking，1975)。有研究者認為，內部不確定性可以使用類似“I am uncertmn……”的句式表達，而外部不確定性可以使用類似“It is uncertain……”的句式表達(Teigen&Brun，1999)。即，通過改變文字概率前面的主語可以分別表示不同類型的不確定性。有研究者曾發現被試用文字概率表達內部不確定性時能夠比表達外部不確定性激發出更大的責任感和確信感(Fox&Irwin，1998)。有研究者(Dieckmann，Mauro，&Slovic，2010)認為數字概率也可以通過不同的句式結構表達內部不確定性或外部不確定性(如，“The probability that…is 10％”)，但是在他們的實驗中，這種操作沒有對可能性判斷、危害知覺和信息來源可信度等造成影響。不過，目前針對文字概率和數字概率的內／外不確定性的研究還不多，這種特性是否只在文字概率上體現還需要進一步驗證。

3.3文字概率的自身／他人區別

研究者們發現，在預測未來事件時，人們傾向于認為正性事件更可能發生在自己身上，而負性事件更可能發生在別人身上，這種現象被稱為“不切實際的樂觀(unrealistic optimism)”(Weinstein，1980；Weinstein&Klein，1996)、“比較性樂觀(comparative optimism)”或者“自我服務(self-serving)”。正如《周易》震卦上六辭曰：“震不于其躬，于其鄰；無咎。”指的就是“雷不擊自身，而擊鄰人”。Smits和Hoorens(2005)發現，人們在使用文字概率時會表現出“不切實際的樂觀”；同一個文字概率詞(如“likely”)，當分別用來形容自身或者他人未來發生某事的可能性時，會出現解釋偏差，即分別將這兩種情境中的“likely”解釋成不同水平的數字概率值。具體來說，當讓被試預測自身將遭遇某種“不幸”的可能性時，預測結果相對較小；當讓被試預測他人將遭遇某種“不幸”的可能性時，預測結果相對較大。但是，當預測事件變成“幸運”時，預測結果發生反轉。這表明當用文字概率預測未來事件發生的可能性時，預測自我還是他人會對預測結果的解釋造成影響。

3.4文字概率的運動特性

在研究文字概率的語義特性時，我們注意到它還具有第4個特性——運動特性，即，文字概率更適合表達“變化”的不確定性，而數字概率更適合表達“不變”的不確定性(許潔虹，2009)。“變化”的不確定性和“不變”(predetermined)的不確定性是兩種看待不確定性的觀點，在不同的宗教思想和不同的預測理論中可見一斑。“變化”的觀點認為不確定性或可能性是在不斷變化發展的。佛教講究的“因果輪回”就在強調世人的命運是隨著自己種下的“業”發生變化的，所謂“放下屠刀，立地成佛”；古老預測理論的經典《周易》在指導人們預測未來事件時也特別注重采用變化的視角，子日：“知變化之道者，其知神之所為乎”(《系辭上傳》)。“不變”的觀點認為不確定性或者可能性是被某些力量或規則所決定的。基督教的教義強調是上帝創造并決定著一切，希波主教奧古斯丁認為“人注定要犯罪并且活在罪中，無法自拔自救，因為他們一生一世擁有原罪”；現代的概率理論認為事件的可能性遵循著某種數學規律(等可能原則、貝葉斯定理等)，其概率分布函數可被事先決定。這種基督教思想和概率預測理論都暗示著不確定性是不可改變的。在許潔虹的實驗中發現，當請個體預測有生命物發生某事的可能性時，其更偏好使用文字方式，而當請個體預測無生命物發生某事的可能性時，其更偏好使用數字方式；當給個體呈現文字方式的預測時，其認為被預測的主體更可能是有生命物，而當給個體呈現數字方式的預測時，其認為被預測的主體更可能是無生命物。即被試將“文字概率”與“生命”連在一起，而將“數字概率”與“非生命”連在一起。因為生命比非生命更具有運動性和變化性，可以看作是“運動”和“變化”的某種代理(proxy)，所以該實驗結果意味著，文字概率除了具有以上3種語義特性外，它還具有運動特性，更適合表達“變化”(changeable)的不確定性。

3.5語義特性的作用和問題

文字概率的語義特性對人們不確定信息的交流和風險決策起到一定的輔助作用，能夠提供額外的“質”性信息。Teigen和Brun(1999)指出，當我們把文字概率向數字概率轉換的時候(如代表性函數)，文字概率是被放在“量”的維度上進行測量，此時文字概率表現出模糊性。但是當我們從更“質性”的角度研究文字概率時，那么文字概率會比數字概率表現得更為精確。首先，從對文字概率方向性的介紹來看，文字概率能夠精確地指示出表達者所強調的重點是在于事件的發生還是不發生。其次，人們可以通過文字概率區分出“內部不確定性”和“外部不確定性”。再次，文字概率的運動特性能夠傳達出所預測的不確定性或概率仍然處于動態變化中的信息。最后，不同方向性的文字概率詞匯的選擇能夠反映出人們是在進行上行比較還是下行比較。Juanchich等(20io)的研究發現，人們選擇哪種方向性的文字概率詞匯主要取決于人們是在上行比較還是下行比較。上行比較指先呈現可能性小的情境，再呈現可能性大的情境，然后請被試選擇某個文字概率詞匯以表達后者的不確定性水平，此時人們更傾向于選擇積極性詞匯(如likely)；而下行比較指先呈現可能性大的情境，再呈現可能性小的情境，然后同樣請被試選擇某個文字概率詞匯以表達后者的不確定性水平，此時人們更傾向于選擇消極詞匯(如unlikely)。

但是文字概率的語義特性也能夠給不確定信息溝通和風險決策造成一定的問題。其一，因為相同的文字概率用在自己和他人身上的意義不盡相同，所以使用文字概率預測自我和他人的不確定性時，預測結果的變異性增加，做出客觀解釋的難度也增大。其二，通過操縱不同方向性的文字概率詞匯的選擇，信息的發布者能將人們對風險和不確定性的感知導向預想的方向，有時甚至偏離真實客觀的可能性，這會對人們決策和預測造成干擾。首先，文字概率的方向性會影響人們的風險決策行為。例如，在醫療決策中，人們經常要根據醫生對療效的描述來決定是否接受某種治療措施。實驗發現，如果分別使用“somepossibility”和“quite uncertain"形容某種療法的有效程度，接受前一描述方式的被試有90.6％的人愿意采用那種治療措施，而接受后一描述方式的被試僅有32.4％愿意采用(Teigen&Brun，1999)。其次，文字概率的方向性會影響人們對他人風險決策行為的預測。例如，在實驗情境中給被試呈現三個試圖戒掉煙癮的人對各自戒煙成功可能性的描述，分別使用“a slight hope”、“a littledoubtful”和“40％”，然后請被試預測這三人是否會參加相應的戒煙課程。結果顯示，當使用“40％”或“a slight hope”時，有70％的被試認為此人會參加戒煙課程，而使用“a little doubtful”時，只有20％的被試認為此人會參加戒煙課程，盡管“aslight hope”和“a little doubtful"被控制組的被試分別轉換成數字概率“42.2％”和“38.2％”0Teigen&Brun，1999)。

4總結與展望

綜上所述，文字概率相對于數字概率具有模糊性、非概率運算性和語義特性等特征，這些特征使得人們在選擇和使用文字概率時不同于數字概率，進而對人們的不確定信息溝通和風險決策產生不同的影響。整體上說，數字概率是一種更精確的風險表達方式，在風險溝通時人們對其能比較客觀地傳遞、解釋和利用，這也是某些研究者提倡使用數字概率溝通風險的原因。但是，文字概率由于各種語義特性的存在，使其在表達風險水平的同時，還能夠表達額外的信息，如傳達者的主觀不確定性、不確定信息的方向性、不確定信息的變化性等等，這些額外信息會對人們的決策產生影響，成為風險溝通中一種可以操縱個體風險意識和風險判斷的有效手段。當然，文字概率的上述特征也為預測事件的不確定性以及風險溝通和風險決策帶來一定的問題，如：模糊性會影響文字概率在不同個體、不同情境之間傳遞時的意義解釋，甚至帶來兩類溝通悖論；非概率運算性會使人們表現出諸如框架效應之類的非理。積極文字概率詞匯所對應數字概率均值略高于消極文字概率詞匯，但是這種差異不具有跨情境和跨詞匯一致性，而且這種差異很小，不足以解釋被試所做預測的差異量(70％vs 20％)。性行為；某些語義特性(如方向性、自身／他也人特性)會使預測和表達不確定性時的客觀性受到一定程度的損害。是否使用文字概率作為不確定信息溝通的方式以及風險決策的信息基礎，還需要結合具體的行為目標，在不同的任務情境中具體分析。

在以往的風險決策研究中，大多數使用數字概率來測量人們對風險或不確定性的判斷，使用文字概率的研究非常少。既然文字概率和數字概率具有許多不同的特性，那么有理由推測，使用文字概率測量的風險決策研究應該會發現一些與數字概率不同的實驗結果：譬如上文所提到的“框架效應”；另外，Honda和Yamagishi(2009)在測量文字概率的方向性時也發現，當使用數字測量不確定性時，文字概率在控制其“代表性函數”的峰值之后，其方向性沒有對感知到的不確定性造成影響，但是當使用文字標識的量尺測量不確定性時，文字概率的方向性表現出系統性的影響，這說明實驗結果有時會隨著測量方式的改變而發生變化。文字概率在人們日常生活中被更廣泛更自然的使用，所以研究涉及文字概率的風險決策更能揭示出人們在日常生活情境中是如何處理風險的，并為人們的風險決策提出更切實可行的建議。不過，使用文字概率測量風險的弊端是不易進行量化統計分析，而且被試之間選擇的文字概率也不一定具有一致性。對此的解決方式之一是構建每個被試的文字概率等級順序列表(Wallstenet al.，1993；Dhami&Wallsten，2005)，即讓被試自己選出能夠覆蓋0—100％的文字概率詞匯，并將其排序使之與特定數字概率或數字等級相對應。此外，不同的文字概率詞匯具有不同的使用頻率，因此在用文字概率測量人們對風險或不確定性的判斷時，還要特別注意詞匯頻率的匹配和控制等問題。

文字概率和數字概率在進化歷史上出現時間不同，隸屬的發展領域(語言和數學)也不同，所以其特征上的差異可能不止于以上所述。例如文字概率的非概率運算性表明，人們傳達或接收文字概率表征的信息時不會按照概率規則進行審慎地運算，文字概率更多地引發直覺式思考，數字概率更多引發分析式思考。這與近些年來研究者們一直關注的“雙系統模型”(Mukheriee，2010；Strack&Deutsch，2006)非常相似。在雙系統模型中，一種系統的加工過程表現為直覺性的，自動化的，自然的，描述性的，體驗式的；而另一種的加工過程表現為分析式的，文字的，審慎的，理性的。Mukherjee將前者叫做基于情感的聯想式模型(associative affect-based mode，A模型)，將后者叫做基于規則的審慎式模型(deliberativerule-based mode，D模型)。很有可能文字概率與A模型聯系得更為緊密，反映出個體對風險的直覺性情緒性評估，而數字概率與D模型聯系得更為緊密，反映出個體對風險的分析性規則性評估。未來的研究可以考慮以雙系統模型為基礎，探索文字概率和數字概率在不確定性預測和風險決策中的獨特作用。其次，在神經經濟學的研究中，決策行為的皮層表征受到越來越多的關注，尤其是涉及概率的風險決策的腦區，例如有研究中發現，皮層下腦區(古老系統)主要表征決策中的情感成分，而皮層腦區(新皮層)主要表征數字概率成分。同樣作為概率的表征形式，文字概率和數字概率是被不同的腦區表征，還是被相同的腦區表征呢?對于這個問題的回答有助于加深對“概率”和“風險”的神經機制的理解，如果文字概率和數字概率能夠被相同的腦區表征，那么說明在大腦中存在某個區域主管對“概率”和“風險”的知覺和加工；如果文字概率和數字概率沒有重合的表征腦區，那么說明大腦并沒有對“概率”和“風險”形成模塊化的表征區域，也許只是彌散地分布于其他的認知加工功能之中。

隨著世界一體化、全球化的發展，風險溝通越來越多地在不同文化背景的群體間進行，如何促進這種跨文化風險溝通的效果對國際間的合作、沖突解決有重要的指導意義。因此，不同文化背景的個體表征文字概率和數字概率的認知特點(Cohn，Cort6s Vazquez，＆Alvarez，2009；Doupnik＆Richter,2004；Salleh，Gardneg Sulong，&McGowan，2011；許潔虹，2009；許潔虹，李紓，2007)成為研究者們關注的問題之一。上文所述的文字概率的各種特征和問題主要是基于英語概率詞匯研究所得到的結果，對于其他語言文字中的概率詞匯來說，是否具有相同的認知加工特點仍是一個值得探討的問題。

文字概率和數字概率同樣作為不確定性的表達方式，在人們的風險溝通和決策中發揮著重要的作用，但是似乎之前的研究過分偏重于對數字概率，使得文字概率的特征和應用沒有被充分重視和推廣，特別是對于中文的文字概率詞匯的研究更是少之又少。今后的研究還需要給予文字概率更多的關注，使其成為研究人們在不確定情況下的決策規律的另一個重要的突破口。