含無序量測的多傳感器目標跟蹤濾波算法

蔣春蕾

西昌學院汽車與電子工程學院，四川西昌 615013

在飛行器的分布式多傳感器融合跟蹤系統中，由于通信鏈路隨機時間延遲，以及各傳感器的量測預處理時間不同，多傳感器量測數據通過多條數據鏈路傳輸到中心處理器時，常會發生多傳感器量測數據不按正常時序到達融合中心的情況，即出現所謂的無序量測現象(Out Of Sequence Measurement, OOSM)。目前針對此問題主要的處理方法分為4類[1]：重新濾波法、數據緩存法、丟棄滯后量法和直接更新法。其中，重新濾波法、數據緩存法的計算量較大，影響了飛行器跟蹤系統的實時性；丟棄滯后量法容易造成大量有用信息的丟失，導致跟蹤系統的精度嚴重下降；直接更新法的存儲量和計算量都很小，濾波輸出沒有滯后，而且具有潛在的高精度濾波性能，是實時多傳感器組合跟蹤系統的最佳選擇。本文在直接更新法的基礎上，提出一種新的飛行器跟蹤濾波方法，解決分布式多傳感器目標跟蹤濾波中的無序量測問題，實現對飛行目標的高精度跟蹤。

1 描述飛行器空間狀態的常用坐標系

用于測量飛行器狀態需要用到的坐標系主要有：地心慣性坐標系、星體坐標系等。坐標系的3個基本要素是坐標原點、基本平面(x軸和y軸所在平面)及正法向(右手系)，基本平面上的主方向(z軸方向)。

1.1 地心慣性坐標系

該坐標系的坐標原點為地球質心Oe，其x軸指向標準歷元2000.0(即2000年1月1日12時)的平春分點，基本平面為該標準歷元時刻的平赤道面，z軸與x軸垂直，并指向該標準歷元時刻的平天極，z軸在基本平面內與x軸、y軸構成右手系。

1.2 星體坐標系

在該坐標系中，坐標原點Os為觀測衛星的質心，基本平面為觀測衛星的軌道面，z軸從坐標原點Os指向地球質心Oe，x軸在基本平面內與z軸垂直并指向衛星運動方向，z軸垂直于基本平面并與x軸、y軸構成右手系。

1.3 坐標系的相互轉換

地心坐標系與星體坐標系的坐標轉換可分2步進行。首先進行坐標平移，將地心慣性系中的坐標平移到以觀測衛星質心Os為原點的空間坐標系；其次進行坐標旋轉，將以觀測衛星質心Os為原點的空間坐標系的坐標轉換到相應的星體坐標系。具體轉換方法詳見文獻[2]。

2 飛行器運動狀態模型和測量模型

2.1 飛行器運動狀態模型

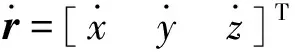
(1)

則飛行器運動的狀態微分方程為：

(2)

其中F(·)表示狀態變量X的非線性變換。

μ

(3)

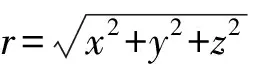
2.2 飛行器姿態測量模型

觀測模型描述了目標的三維空間位置到目標像平面位置的映射過程。設地心坐標系下的目標位置為r=[xyz]T，衛星位置為rs=[xsyszs]T，(·)T表示矩陣轉置，則將目標位置r映射到像平面位置需要經過一系列坐標系轉換，依次為地心坐標系?軌道坐標系?星體坐標系?傳感器坐標系?像平面坐標系。

根據成像模型的逆過程計算出目標飛行器所在的方位角βk和俯仰角εk，其定義分別如下：

(4)

(5)

將測量矢量定義為Z(k)=[βkεk]T，則測量矢量可以表示為狀態變量X的非線性函數：

Z(k)=H(X(k))+n(k)

(6)

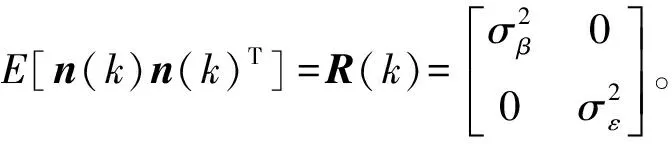
3 跟蹤濾波算法與仿真

3.1 擴展卡爾曼濾波算法

由于目標飛行器中段的狀態方程是非線性連續方程，測量方程是非線性離散方程，這里采用擴展卡爾曼濾波(Extend Kalman Filter, EKF)方法[3]來估計目標飛行器的狀態，首先需要對狀態方程和測量方程進行離散化和線性化，其處理過程如下：

對目標飛行器的狀態微分方程(2)式進行離散化，可得：

(7)

當時間間隔tk+1-tk=T足夠短時，F(X(t))可以在tk附近展開為Taylor級數：

F(X(t))≈f(X(k))+A(X(k))·

F(X(k))·(t-tk)

(8)

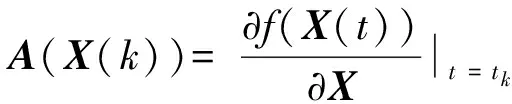
X(k+1)=X(k)+F(X(k))·T+

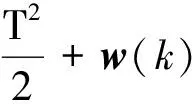
(9)

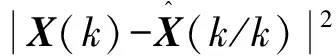
由(2)式及矢量微分法則[4]，A(X(k))可以表示如下：

(10)

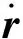
//(k/k))·T+

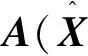
(11)

根據狀態轉移矩陣Φ(t,tk)的定義[5]，可以將其在tk附近展開為Taylor級數：

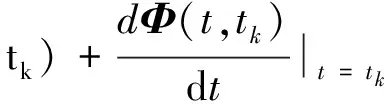
(t-tk) +O(t-tk)

(12)

根據狀態轉移矩陣的性質可得：

Φ(tk,tk)=I

(13)

(14)

將上兩式分別代入(12)式，可表示為：

Φ(t,tk)=I+A(X(k))·(t-tk)+O(Δt)

(15)

同樣地，對連續狀態轉移矩陣進行離散化后可得：

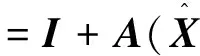
(16)

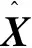
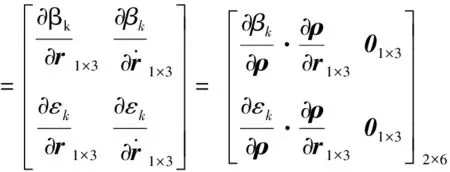
(17)

由式(4)和(5)及文獻[2]中的坐標轉換公式ρ=GT(rT-ρO)，可得：

(18)

(19)

(20)

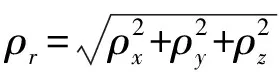
將狀態方程和測量方程線性化、離散化后，即可將其代入如下所示的擴展卡爾曼濾波公式進行迭代計算。為便于表示，這里將遞推的時刻轉換為矩陣的下標來表示。

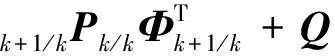
(21)

在這里Q矩陣表示由于非線性狀態方程線性化時引入的誤差，一般可通過經驗選取為較小的常數矩陣[6]。

計算濾波增益矩陣：

(22)

計算狀態濾波更新及相應的協方差矩陣：

(23)

Pk+1=(I-Kk+1Hk+1/k)Pk+1/k

(24)

3.2 多步滯后無序量測處理算法

觀測衛星系統在下傳角軌跡數據時，可能由于傳輸距離或者預處理時間的不一致，導致較早的測量數據反而較晚到達數據融合中心的現象，即所謂的無序量測現象，該情況如圖1所示。

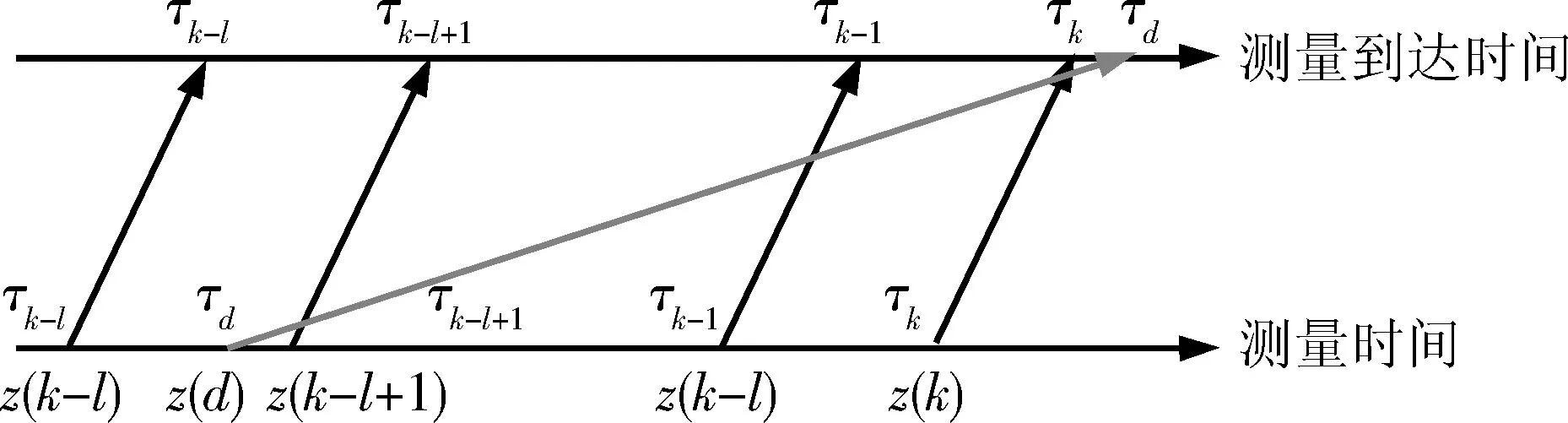
圖1 無序測量示意圖

目標飛行器的中段運動模型可視為二體運動模型，其狀態方程和測量方程可表達式為：

X(k+1)=f(X(k),k)+w(k)

(25)

Z(k)=h(X(k),k)+n(k)

(26)

其中噪聲協方差為：

E[w(k,j)w(k,j)T]=Q(k,j)

E[n(k)n(k)T]=R(k)

(27)

在無序量測Z(d)到達之前，系統狀態已經更新到t(k)狀態。根據3.1節中擴展卡爾曼濾波算法得到最新的預測估計狀態和協方差：

E[X(k),Zk]

(28)

P(k|k)cov[X(k),Zk]

(29)

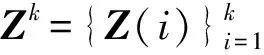
Z(d)=h(X(d),d)+n(d)

(30)

計算從t(d)時刻到t(k)時刻的預測方程和預測協方差：

E[X(k),Zd]

(31)

P(k|d)cov[X(k)|Zd]

(32)

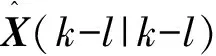
P(d|k-l)=(Φ(k-l))P(k-l|k-l)

(Φ(k-l))T+Q(d,k-l)

(33)

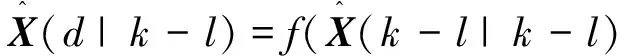
(34)

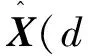
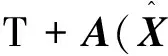
(35)

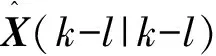
下面給出多步無序量測的計算步驟：

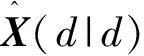
P-1(d|d)=P-1(d|k-l)+

(H(d))TR-1(d)(H(d))

(36)

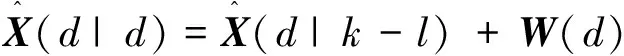
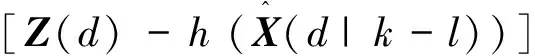
(37)

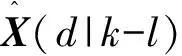
(H(d))TR-1(d)Z(d)

(38)

Step 2：計算從t(d)到t(k)預測狀態方程及協方差：

P(k|d)=(Φ(d))P(d|d)(Φ(d))T+Q(k,d)

(39)

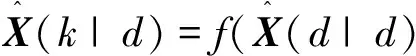
(40)

假設P(k|d)和P(k|k)不相關可得等式：

P-1(k|k,d)=P-1(k|k)+P-1(k|d)

(41)

但是P(k|d)和P(k|k)根據相同的預測模型分享共同的歷史數據(如P(k-l|k-l))，所以兩者是具有相關性的，為了得到獨立的信息，就得去除無關的信息。

P-1(k|d)D=P-1(k|d)-P-1(k|k-l)

(42)

(43)

Step 4：計算狀態濾波更新及相應的協方差矩陣：

P-1(k|k,d)=P-1(k|k)+P-1(k|d)D

(44)

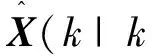
(45)

3.3 算法的仿真分析

仿真場景設置：采用2顆衛星同時對目標飛行器進行觀測，采樣時間間隔為4s，取飛行器在空間飛行的500～600s弧段作為觀測時間段，視線誤差為100μrad。仿真分單步延遲量測、兩步延遲量測和多步延遲量測3種情況進行討論。

(1)單步延遲量測

衛星1的量測數據按正常時序到達中心處理器，衛星2的量測數據固定作單步延遲，圖2為衛星測量時間與到達時間的時序關系描述。

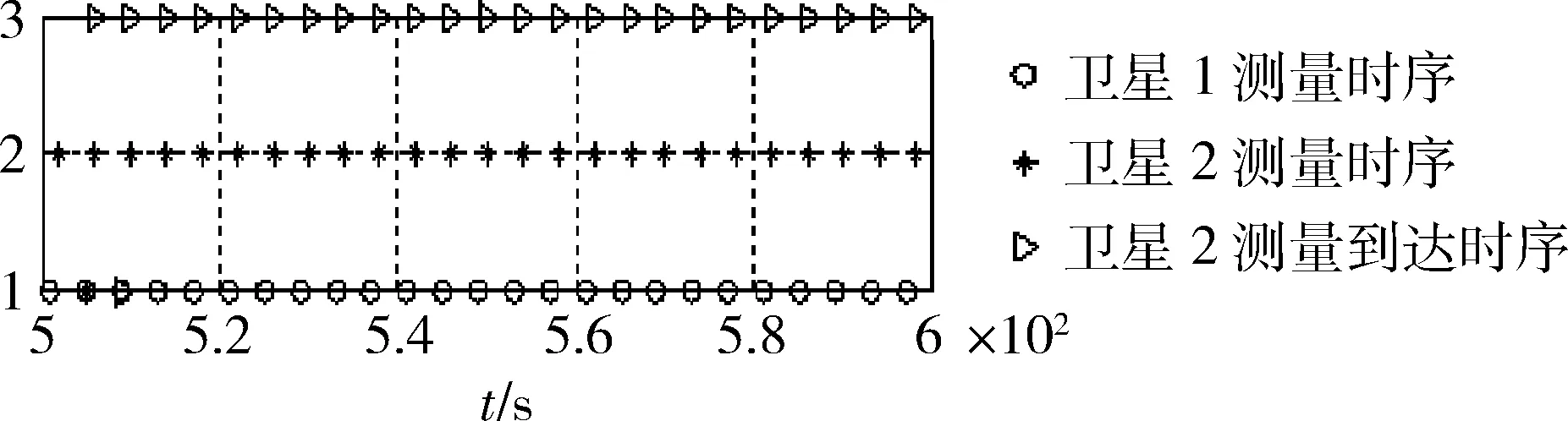
圖2 衛星的測量時間和到達時間描述圖

為了簡化描述，將擴展卡爾曼濾波算法簡稱為EKF，基于擴展卡爾曼的前向預測多步滯后無序量測處理算法稱為EKF-OOSM，CRLB為克拉美羅下限。將本文的EKF-OOSM算法與傳統的丟棄算法、EKF算法進行對比，各算法的仿真結果如圖3所示。

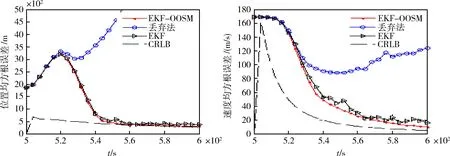
圖3 單步延遲情況的位置速度均方根誤差

(2)兩步延遲測量

將衛星2的測量數據作兩步固定延遲，其它參數設置與單步延遲相同，各算法的仿真結果如圖4所示。

(3)多步延遲測量

將衛星2的測量數據作多步固定延遲，其它參數設置與單步延遲相同，各算法的仿真結果如圖5所示。

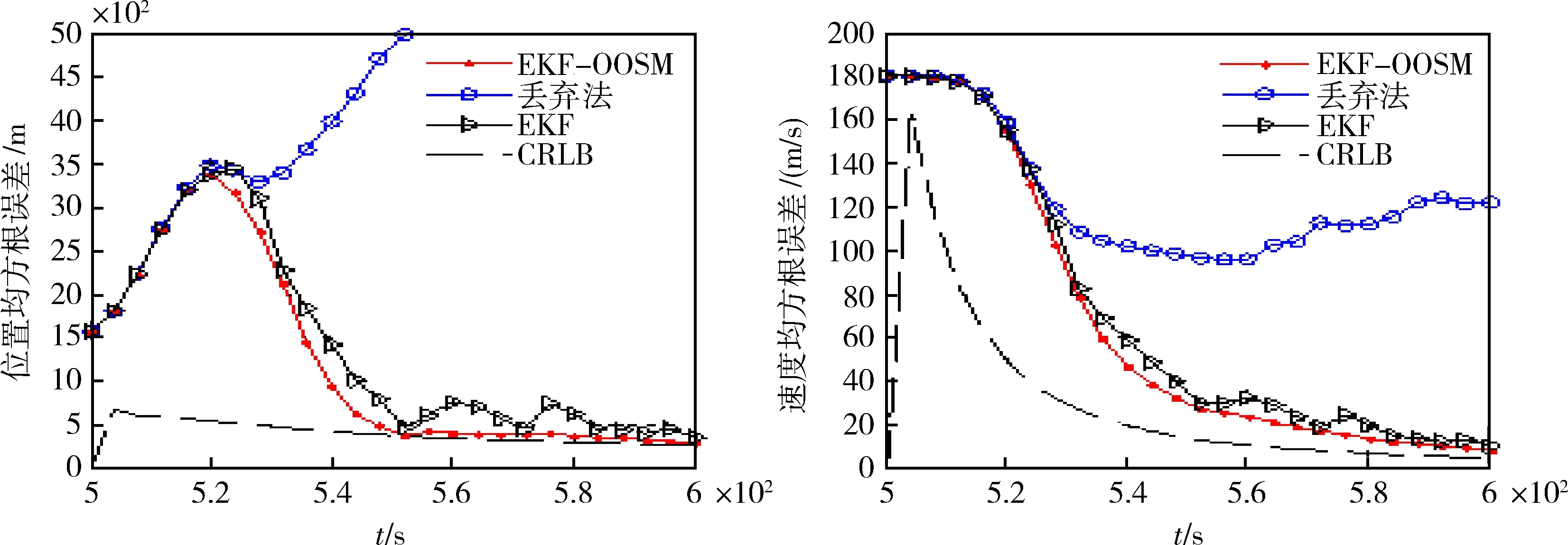
圖4 兩步延遲情況的位置速度均方根誤差

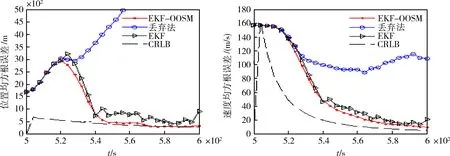
圖5 多步延遲情況的位置速度均方根誤差

從圖3、圖4和圖5的仿真結果可以看出，丟棄滯后量數據的濾波算法(即丟棄算法)的濾波效果很差，測量目標飛行器時得到的位置誤差和速度誤差與克拉美羅下限CRLB相差太大，特別是位置誤差還有可能導致濾波結果不收斂。擴展卡爾曼濾波算法EKF在整個觀測時間內，測得的位置誤差和速度誤差有抖動，濾波效果不平滑，有起伏現象，測量精度不高，其測量的位置誤差、速度誤差較大。與丟棄算法、擴展卡爾曼濾波算法EKF相比，采用EKF-OOSM濾波算法得到的目標飛行器的位置誤差、速度誤差較小，接近理想狀態的克拉美羅下限，而且在整個觀測時間內，濾波結果較為平滑，測量誤差收斂性較好，能夠滿足對目標飛行器數據的精確處理要求。

4 結束語

本文提出了一種針對無序量測數據的多傳感器目標跟蹤處理算法。首先針對多傳感器系統對目標飛行器的跟蹤測量問題，介紹了地心慣性坐標系和星體坐標系的定義及轉換公式，在此基礎上給出目標飛行器的運動狀態方程和測量方程，然后結合擴展卡爾曼濾波算法，推導了基于擴展卡爾曼濾波的前向預測多步滯后無序量測處理算法，最后分別對不同時間步長滯后的情況下目標飛行器跟蹤測量問題進行了仿真分析，仿真結果表明采用該算法處理目標飛行器的位置和飛行速度，得到的誤差較小，在整個觀測時間內，測量誤差的收斂性較好，可以實現對目標飛行器的精確測量和跟蹤。

參 考 文 獻

[1] 韓崇昭, 朱洪艷, 段戰勝. 多源信息融合[M].北京: 清華大學出版社,2006:25-35.

[2] 肖業倫.航天器飛行動力學原理[M].北京:宇航出版社,2005:203-205.

[3] 李強.單星對衛星目標的被動定軌與跟蹤關鍵技術研究[D].長沙:國防科技大學,2007.

[4] 葉其孝,沈永歡.實用數學手冊(第2版)[M].北京:科學出版社,2006.

[5] Steven M. K. Fundamentals of Statistical Signal Processing Volume I: Estimation Theory [M].Pearson Education, Inc, 1993.

[6] 盛衛東，林兩魁，安瑋，周一宇.基于全局最優的被動多傳感器多目標軌跡關聯算法[J]. 電子與信息學報,2010,37(7):1621-1625.(Sheng Wei-dong,Lin Liang-kui,An Wei,Zhou Yi-yu.A Passive Multisensor Multitarget Track Association Algorithm Based on Global Optimization[J].Journal of Electronics and Information Technology,2010,37(7):1621-1625.)