基于數據挖掘技術的網絡流量分析預測系統研究

車旭民

(南京曉莊學院，江蘇 南京 211171)

0 引言

隨著全球信息化進程的加快，網絡尤其是Internet作為現代信息社會最重要的基礎設施之一，已滲透和影響到社會的不同領域，成為社會進步和國家發展的基本需求，是未來知識經濟的基礎載體和支撐環境。信息社會和正在逐漸形成的全球化知識經濟形態對信息網絡管理提出了很高的要求，但Internet網絡在管理方面逐漸暴露出許多缺陷。［1－3］

本文就是在這樣的背景下，研究了網絡流量分析與預測原型。由于該模型采用了數據挖掘技術，且系統能夠通過自學習，對網絡流量數據進行分析，然后進行特征提取，擴大樣本知識庫，不斷提高流量采集的能力。它具有自適應、分布式和面向網絡業務的特點，可以有效地解決現有的許多流量采集系統中的問題。

1 網絡流量及其預測概述

1.1 網絡流量的數據采集

網絡流量數據采集方法主要分為基于網絡探針的網絡流量采集方法和基于網絡流(Netflow)的網絡流量采集方法。在不同的考察層面，兩者具有不同的特性。

1.2 網絡流量的理論分析

當前，廣為流行的網絡體系結構 OSI［4－6］結構系統，采用了7層的層次結構，每層各負責不同的通信功能，所有協議的分層結構如圖1所示。

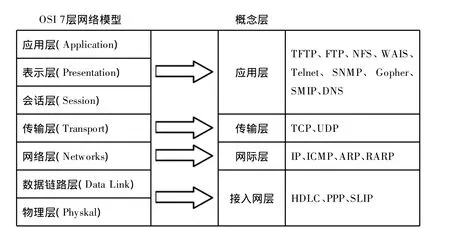
圖1 網絡層次化結構模型示意圖

按照圖1的參考模型，以及數據包的傳輸過程，可以構造一個合適的數據結構，來保存需要的信息。以下根據圖2對協議網絡流量數據封裝和分解進行分析。

圖2 協議網絡流量數據封裝和分解示意圖

2 網絡流量行為預測的具體實現

2.1 k-means聚類算法的改進

針對 k-means聚類算法［7－8］存在的問題，可以考慮采用分層聚合的形式避免這些問題。也即在初始化數據時，將數據集中的每個樣本設置為1個類;計算現有的所有類兩兩之間的距離(相似度)，找出其中距離最近(相似度最大)的2個類;將最近的2個類合并為1個新類，總類數減1;若所有樣本數據合并為1個類或滿足所設定的終止條件時，結束算法;否則，返回計算現有的所有類兩兩之間的距離。

本文研究的k-means聚類改進算法的核心思路如下:

1)以分層聚合的方式，求出最合適的聚類個數k，并找出每個簇中心，如此便可獲取第2步劃分聚類的初始值。

2)利用k-means聚類算法進行迭代重定位運算來優化改進，直到出現較好的聚類結果。

之所以利用此方法，是因為在分層聚合開始時，將每1個數據對象看作是1個簇，因此，對初始聚類中心無特殊要求，如此可以彌補k-means聚類算法對聚類中心的依賴。同時，通過k-means聚類算法的反復優化又對分層聚合所存在的“不可逆轉”的缺陷進行了一定補償。

在實際的網絡流量分析與預測中，可以利用上述算法，依據首重宏觀，由面及點的原則，進行逐步深入的分析。所謂的逐步深入的分析，即采用從網絡到主機逐級細化的分析步驟來對流量數據進行剖析，從宏觀入手了解網絡上流量的變化趨勢開始，逐級細化到掌握主機上流量的狀態。該分析技術主要分為以下步驟［9－10］進行:

第1步，面向網絡的分析，該步驟屬于粗粒度的分析，即了解網絡上整體的、宏觀的流量分布狀況。首先對時間維上的流量數據進行分析，篩選出可能的異常時間點，每1條數據的屬性代表該時刻整個網絡上流量的分布情況，即以P維列向量來描述。本文選取源IP地址、目的IP地址、端口號作為表示流量的特征參數。通過獲取這些特征參數的信息熵，即可以用一個特征向量來表示當前時刻的網絡流量狀態。通過該算法的分析，便可以靈活、準確地區分出網絡中存在的不同流量分布狀態，從而對網絡的流量情況進行總體的、宏觀的把握。

第2步，面向主機的分析，該步驟屬于細粒度的分析，即了解網絡流量狀態在各個主機上的分布情況。針對第1步分析中分離出的可能存在于異常時段內的數據點，進行進一步的分析。此時每1條數據代表該時刻該主機的網絡流量狀態情況，通過選取傳輸層協議(TCP、UDP)的分布情況、平均丟包率以及平均包大小等表征主機流量狀態的參數進行分析，便可以準確定位到可能存在異常的主機，從而為后續的策略制訂及所需采取的措施提供依據。

在進行分析之前，需要對網絡流量數據集Traffic進行標準化，即通過將屬性數據按比例縮放，使之落入一個小的特定區間。對于本文所使用的這種基于距離的算法，規范化可以幫助防止具有較大初始值域的屬性與具有較小初始值域的屬性相比(如，在一個局域監測范圍內，網絡端口的數量要遠遠大于IP地址的數量)，顯得權重過大。由于本文所選取流量特征熵的取值在［0，log2N］之間，這里的N或為IP地址數，或為網絡端口數，其最大最小值均為已知數據，因此，可以采用最小—最大規范化的方法對原始數據進行線性變化。實驗結果如表1所示。

根據表1可以看出，改進后的算法能夠得到較高且穩定的準確率，針對數據集 Iris、Wine、Traffic均可以得到接近最高準確率的聚類結果。產生這種結果的原因是改進后的算法首先利用分層聚類的方法來確定初始聚類中心，而分層聚類對于初始聚類中心是沒有要求的，因而產生的初始聚類中心比較符合數據實際分布，也就更適用于對實際數據的聚類。

2.2 網絡流量行為預測的實現

令k為改進的k-means聚類算法的輸入參數，其含義為該算法分割并計算網絡流量數據集后輸出的聚類的數量。網絡流量數據集由n個模式(Patterns)組成。在本文算法中，使k=3，在進行初始化時，根據k隨機地從n個模式{i1，i2，…，in}中找出 k 個原型(Protypes){W1，W2，W3，…，Wk}，故:

初始化{W1，W2，W3，…，Wk}，其中，Wj=ii，j∈{1，2，…，k}，i∈{1，2，…，n}

使每個聚類Ci與原型Wj對應

Repeat

For每一個輸入向量 ii，其中 ii屬于{1，2，…，n}do

將ii分配給最近的原型Wj所屬的聚類Cj。即:

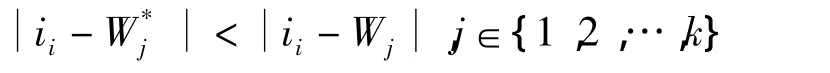
For每一個聚類 Cj，其中 j屬于{1，2，…，k}do

將原型更新為當前的Cj中所有樣本的質心點，并計算錯誤函數

Until E不再明顯地改變或者聚類的成員不再變化

End

其中Cj是第jth個聚類，其值是輸入模式互不相交的子集。

錯誤函數確定聚類的質量。如何選擇恰當的k值，通常來說是一個比較困難的問題。一般來說，k值的選擇和問題域有關，用戶需選擇不同的k值進行實驗。設有n個模式，每1個模式的維數為d，則1個直接k-means改進算法的每1個循環的計算代價可以分解為以下幾部分:

1)以上算法中的第1個For循環所需的時間復雜性。

2)計算質心點的時間復雜性。

3)計算錯誤函數的時間復雜性。

循環的次數與輸入模式的數量及輸入數據有關，可以從幾次到上千次不等。故，k-means改進算法的時間復雜性可以精確地計算出來，這對數據挖掘應用于網絡流量數據大量的模式向量來說尤其重要。

利用k-means改進算法，把采集到的網絡流量數據進行聚類，最終生成如下屬性，如表2所示。

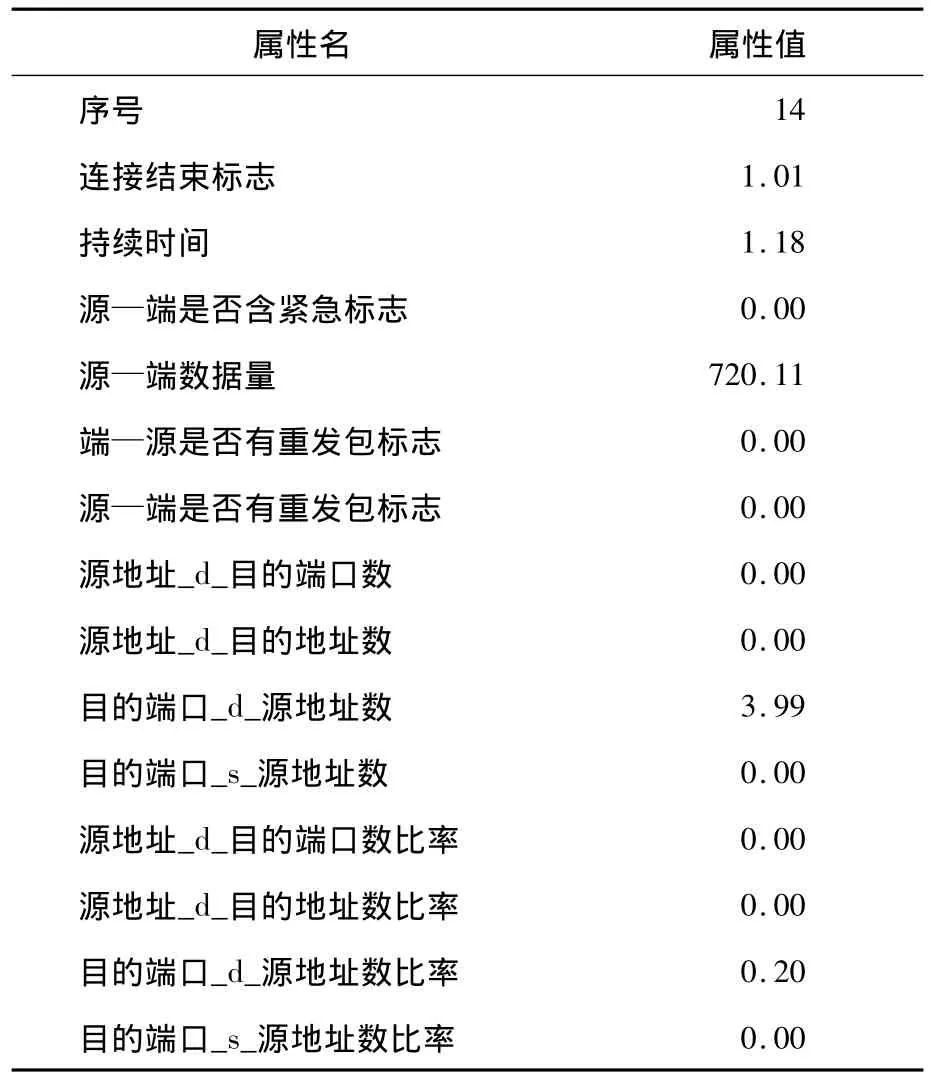
表2 網絡流量數據分流后的屬性表

3 結語

改進的k-means算法相比經典的k-means算法在時間復雜度和聚類準確率上均具有較大的優勢，對于網絡流量數據大量的模式向量，k-means改進算法的時間復雜性可以精確地計算出來，通過仿真實驗表明，該算法達到實際應用需求。

［1］何榮毅.網絡流量監測管理系統的研究與實現［J］.硅谷，2008，4(9):12 －14.

［2］周小勇，胡寧，向楊蕊，等.基于數據流的實時網絡流量分析系統設計與實現［J］.計算機應用研究，2007，8(10):34 －36.

［3］程斌，魏國強，何光營.基于應用層的校園網網絡流量監測與分析［J］.上海電力學院學報，2010，9(1):89 －91.

［4］劉穎秋，李巍，李云春.網絡流量分類與應用識別的研究［J］.計算機應用研究，2008，12(5):39 －42.

［5］匡琳.P2P網絡流量監控技術探討［J］.科技廣場，2008，7(12):45－48.

［8］周宏.校園網上netflow流量監控分析系統的設計與實現［J］.西南民族大學學報:自然科學版，2005，7(3):22－25.

［9］周向軍.校園網流量識別與控制系統的建設［J］.電腦知識與技術，2009，8(14):70 －72 .

［10］黃茹芬.校園網流量測試與分析［J］.福建電腦，2006，32(11):90－92.