汽車驅動橋準雙曲面齒輪齒面測量誤差精確計算

鄧效忠 李天興，2 李聚波 周廣才

1.河南科技大學，洛陽，471003 2.西北工業大學，西安，710072 3.江蘇大學，鎮江，212013 4.哈爾濱精達測量儀器有限公司，哈爾濱，150078

0 引言

汽車驅動橋齒輪作為汽車動力傳動系統中的關鍵零件，普遍采用螺旋錐齒輪中最為復雜的準雙曲面齒輪。準雙曲面齒輪傳動平穩、噪聲低，尤其是其主動輪軸線相對于被動輪軸線的偏置在汽車制造工業中具有特殊的優越性，能使汽車的車身增高或降低，從而提高汽車的越野性能和穩定性。在使用上的諸多優點，使得人們對汽車驅動橋齒輪的嚙合傳動性能要求愈來愈高，其高精度、高速度、低噪聲等高品質性能目標對齒面幾何精度及嚙合傳動質量控制也提出了更高的要求［1－2］。

從外觀上看，汽車驅動橋齒輪與一般弧齒錐齒輪很相似，但是其齒面幾何拓撲結構更加復雜，輪坯的設計計算、制造工藝及機床調整加工等比一般弧齒錐齒輪要繁瑣和困難，與之相應的齒面展成技術、齒面檢測技術以及齒面修正理論都較為落后，丞待進行深入研究。

在美國、日本及德國等汽車制造大國，汽車驅動橋齒輪的數字化閉環制造已經替代傳統制造模式［3－6］，齒面檢測技術已成為加工過程中不可或缺的重要環節，其齒輪產品的幾何精度和嚙合質量等綜合性能非常優越，甚至達到了可互換的程度［7－10］。而在國內，目前廣泛以理論齒面的 TCA分析作為汽車驅動橋齒輪的設計評價方法，以傳統的滾動檢驗作為輪齒嚙合質量檢驗的主要手段，存在切齒調整復雜、質量不穩定、生產效率低下等缺點，這些缺點導致汽車后橋傳動系統嚙合質量、振動噪聲及使用壽命等問題日益突出［2，11］。國內汽車齒輪的配套生產廠家為了提高齒面精度，縮短加工周期，也一直致力于齒輪幾何結構和嚙合性能的改善與提高，除了引進國外先進設備外，大批的國產設備也逐漸應用到汽車生產線中，但齒面精度及接觸區控制效果不佳。問題就在于在檢測過程中對測量隨機誤差源的研究不夠深入，檢測后的數據補償處理及齒面誤差計算不正確或不精確，使得最終得到的齒面誤差失真，從而對實際齒面接觸區調整與修正起到了誤導作用。所以，通過測量模型的正確構建與齒面誤差的精確計算，獲取實際加工齒面的真實誤差，對汽車驅動橋齒輪齒面精度的數字化控制具有重要的現實意義。

鑒于此，本文針對汽車后橋齒輪齒面誤差的計算原理及精確計算方法展開研究，通過對齒面數控展成與檢測的深入分析，基于國產齒輪測量中心的檢測數據，提出了一種汽車后橋齒輪齒面誤差的精確計算方法。該方法有助于準確完成齒面檢測，有效減小測量隨機誤差，從而獲取實際齒面的真實誤差，為改善汽車后橋齒輪齒面幾何精度，提高其嚙合質量提供理論和方法指導。

1 齒面的數控展成與誤差檢測

與一般錐齒輪相比，汽車驅動橋齒輪主動輪的上下偏置以及其螺旋角遠遠大于被動輪螺旋角的特殊性增加了齒輪嚙合的重疊系數，提高了運動的均勻性和平穩性。同時，主動輪齒形曲率變化大和齒面幾何拓撲結構的復雜性［12－13］使得輪齒的齒面解析表達、切齒加工調整及齒面誤差檢測等更加困難。而其特殊的用途與優越的嚙合性能對齒面幾何精度和嚙合性能要求又十分苛刻，因此汽車驅動橋齒輪齒面的數控展成和數字化檢測就成為提高齒面幾何精度及嚙合性能的重要技術手段［14］。

圖1所示為汽車驅動橋齒輪的數控展成模型。在齒輪加工過程中，通過控制3個直線軸（X、Y、Z軸）和2個旋轉軸（A、B軸）的相對位置和運動軌跡（即機床運動參數：X＊、Y＊、Z＊、A＊、B＊等）來確保齒面展成運動的準確性。該數控展成模型中，坐標系Sf（OfXfYfZf）與床身固連；St（OtXtYtZt）和Sw（OwXwYwZw）分別與刀盤和 齒 輪 固 連；Sh（OhXhYhZh） 和Sm（OmXmYmZm）與坐標系Sf平行，分別固連于Y方向滑臺和Z方向滑臺；Oh在Sf中的位置用坐標（X＊，Y＊，0）表示，用以描述X 軸和Y軸自由度；Om在Sf中位置用坐標（0，0，Z＊）表示，用以描述Z軸自由度；St繞坐標軸Zh轉動，轉角為φ；Sp（OpXpYpZp）為輔助坐標系，原點Op位置由機床常數H 和轉角γ（輪坯根錐角）確定，轉角γ描述B軸旋轉自由度；坐標系Sw繞坐標軸Xp旋轉的角度θ描述A軸旋轉自由度。

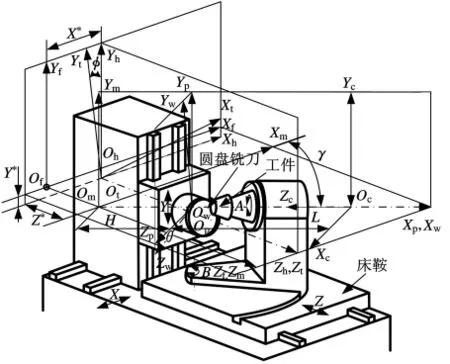
圖1 齒面的數控展成模型

在加工過程中，數控銑齒機的各數控軸聯動，靈活控制被加工齒輪與銑刀盤在空間中的位置和運動，然后通過復合空間運動可完成實際展成運動形成加工齒面。一個齒槽切削完畢，各數控軸返回到初始位置，工件箱后退，同時被加工齒輪轉過一定的分齒角度，進入下一個切齒循環。反復進行即可完成所有齒面的加工。

數控展成的實際齒面只有與理論設計齒面幾何結構相一致才能確保齒面嚙合性能最優。這就需要在齒輪測量中心上通過對齒面進行檢測來獲取實際加工齒面偏離理論設計齒面的法向偏差。圖2所示為汽車驅動橋齒輪齒面誤差的檢測模型。在該模型中，Sw（OwXwYwZw）為在數控展成中與輪坯固連的工件坐標系，測量坐標系Sc（OcXcYcZc）為左手坐標系，固連于齒輪測量中心上，原點Oc位于測量中心回轉工作臺中心，坐標軸Xc和Yc分別與Sp的坐標軸Yp和Zp平行，Zc與Xp反向。直線位移L與角位移θ分別確定了被測齒輪和被測齒面在坐標系Sc中的具體方位，二者可在測量過程中通過間接測量或計算得到。

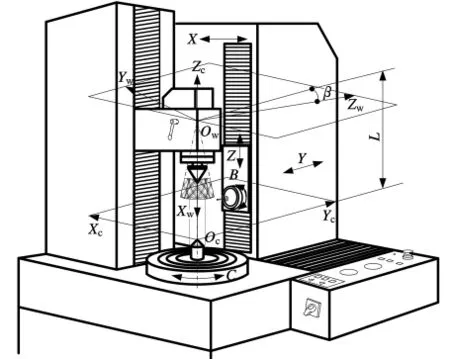
圖2 齒面的數字化檢測及模型

齒輪測量中心采用坐標測量原理，實際上是圓柱（極）坐標測量機［4］。在齒輪測量過程中，中心計算機根據被測齒輪齒面的理論數據控制各直線軸（X、Y、Z軸）和旋轉軸（C軸）的運動，同時齒輪不斷轉動使每個被測點法線方向的Y軸分量接近于0。與一般錐齒輪的齒面檢測相比，由于汽車驅動橋齒輪齒面曲率很大，因此需要控制B軸旋轉一定角度，保證一維測頭始終沿著被測點的法線方向與齒面靠近、接觸。在測頭沿齒輪齒面運動的過程中，計算機不斷采集各坐標軸的實際位置，并存儲起來，這些數據記錄了被測齒輪實際加工齒面的數據，由計算機與理論齒面進行比較處理后得出實際齒面的齒面誤差。

2 測量齒面的數字化處理

由齒面展成與檢測的運動分析可知，汽車驅動橋齒輪的齒面幾何完全取決于數控機床和齒輪測量中心運動時的自由度參數。根據齒輪嚙合理論和微分幾何學原理，齒輪齒面與刀具切削面是一對共軛曲面，通過齒面展成的運動關系和嚙合方程，可以確定理論齒面的解析表達式。

假設機床運動參數Φj（j為機床運動參數個數，j＝1，2，…，m）已知，經過一系列的空間坐標變換與推導過程［11］，可以得到工件坐標系Sw下的理論齒面H0和單位法矢n0：

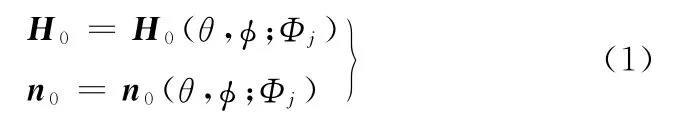
為了便于齒面的精密測量與數據處理，需要對齒面點進行數字化處理，并確定各點的空間坐標和法線方向。根據美國齒輪制造商協會標準，一般取45個齒面點［11，13］，如圖3所示。

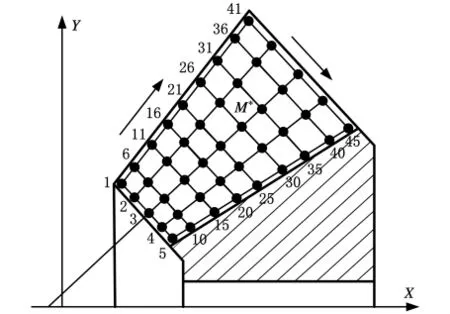
圖3 測量齒面的數字化

M＊為齒面上任一被測點。由齒面的平面幾何關系可確定M＊點在旋轉投影面中的坐標（x＊，y＊），該點與理論齒面H0上第i點（i為齒面測量點序號，i＝1，2，…，45）的坐標（xi，yi，zi）有如下關系：

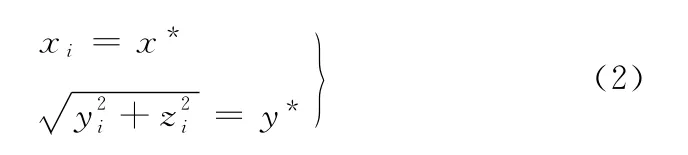
機床運動參數Φj已知，利用優化方法或數值迭代求解式（2），可得到各被測點的齒面參數θ和φ，將其代入式（1）即可得到Sw下的齒面理論坐標和法矢。

坐標系Sw下的理論齒面H0（θ，φ；Φj）和法矢n0（θ，φ；Φj）經過由Sw到Sc的空間轉換矩陣Mcw的變換，即可得到Sc下的理論齒面H（θ，φ；Φj）和單位法矢n（θ，φ；Φj）：

式中，β為坐標系Sc與Sw的轉角偏移量。

從理論上講，齒面檢測后得到的是測球球心的運動軌跡坐標，因此需要對理論齒面進行測頭半徑補償處理。假設測頭半徑為ρ，得到Sc下測頭的理論運動軌跡面He：

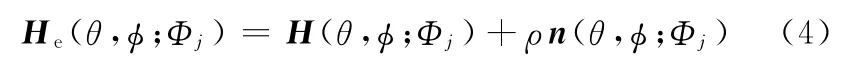
這就是齒面檢測所必需的理論數據，同時也是進行齒面誤差精確計算的基礎。齒輪測量中心可以根據此數據完成整個齒面檢測。

3 齒面誤差的精確計算

在汽車驅動橋齒輪的設計與加工過程中存在許多影響齒面精度的因素，如切齒計算的近似性、機床幾何及運動精度誤差、熱力變形、機床運動調整誤差及刀盤誤差等。這些因素的存在造成了實際加工齒面偏離理論設計齒面，產生齒面誤差。生產實踐和統計學原理證明，汽車驅動橋齒輪的這種齒面誤差是各種精度影響因素的綜合反映，具有一定的穩定性和重復性，能夠被測量和儲存，因此就可以在重復加工中進行修正補償來減小或消除。在實際的加工測量過程中發現，切齒計算誤差、機床幾何及運動精度誤差、熱力變形等影響因素的修正補償均可以通過機床運動參數和刀盤參數來予以轉化或替代，所以借助于機床運動參數和刀盤參數的修正可以達到消除或減小齒面誤差的目的［13］。因此，真實齒面誤差的獲取和精確計算就成為改善齒面幾何精度的前提條件。

如圖4所示，齒面誤差δ的計算原理大體分兩種。

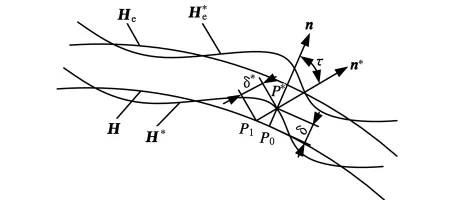
圖4 齒面誤差計算原理

（1）方法1。齒面誤差δ通常在H 的法線方向n上進行度量，定義為實際齒面H＊偏離理論齒面H 的法向距離［15］。對理論齒面H 上一點P0，過其法矢n，找到與P0對應的實際齒面H＊上的點P＊，計算這兩點之間的偏差即為齒面加工時在P0點所形成的齒面誤差δ：

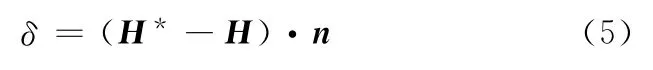
圖4中P0P＊是齒面誤差δ的幾何描述。

（2）方法2。齒面誤差的存在使得實際齒面H＊的法線方向n＊往往偏離理論法線n，以實際齒面點P＊為初始基準點，沿實際齒面法矢方向n＊找到理論齒面上與實際齒面點P＊對應的點P1，對應點之間距離P1P＊即為齒面誤差δ＊：

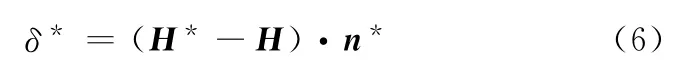
圖4中，P1P＊是齒面誤差δ＊的幾何描述。

令τ為法線n＊過P＊與n的微小夾角，即實際齒面法矢因齒面誤差的影響而在空間轉過的角度（圖4）。兩種齒面誤差計算方法的差異的數學描述為

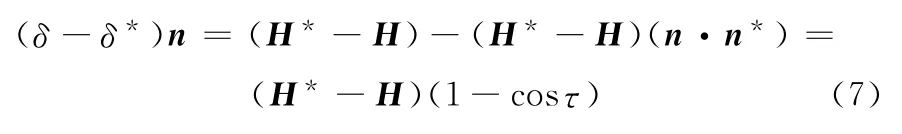
τ一般較小，將cosτ展開為級數并略去高次項，式（7）可表示為

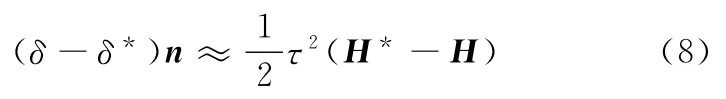
可以看到，兩種齒面誤差分析模型計算值的差異僅與τ和δ相關。τ決定于（n，n＊），δ決定于實際齒面精度。若齒面精度較高，τ和δ就較小，兩誤差模型的差異將十分微小，可忽略不計。但汽車驅動橋齒輪的齒面曲率變化較大，這種差異不容忽視。方法2由實際齒面點尋找理論齒面上對應點時，理論齒面已經解析表達，避免了齒面重構時的擬合誤差；方法1由理論齒面點尋找實際齒面上對應點時，需要對檢測數據進行曲面重構，這樣必然帶入擬合誤差，有可能掩蓋真實加工誤差，不利于齒面精度評價和機床參數反調。但是，在齒面測量過程中，采樣點的個數遠遠大于理論齒面測量點的個數，若采用非均勻有理B樣條對實際齒面測量點進行擬合，必有較好的保凸性，不會造成實際加工信息損失，有利于確保評定精度。另外，汽車驅動橋齒輪齒面在數控展成和誤差檢測中都是以理論設計齒面為基礎的，因此，無論是從誤差評定的準確程度，還是數控展成和誤差檢測的便捷程度，選用方法1來分析與計算齒面誤差將更加準確方便。

由式（5）可知，H上每一點均有唯一一個δ與之對應，因此，δ是H上點的函數，即曲面坐標（θ，φ）的函數，而（θ，φ）又由機床運動參數Φj決定，即Φj是δ的參變量。所以

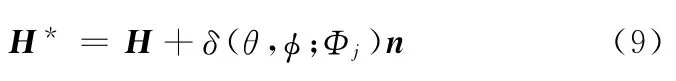
實際齒面的法線n＊造成了空間夾角τ的存在，會對齒面的測量產生一定影響，是測量誤差的來源之一。n＊可表示如下：

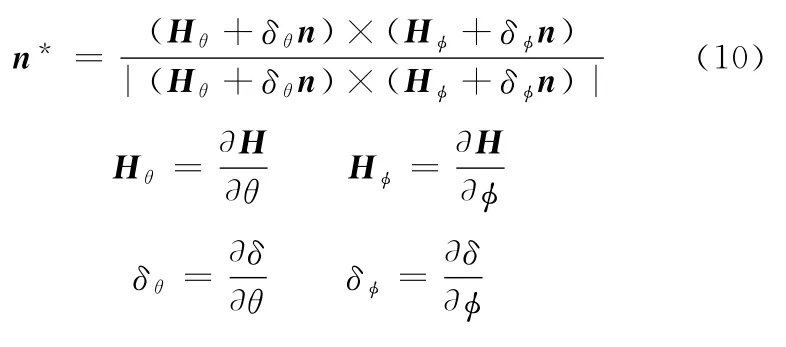
值得一提的是，在汽車驅動橋齒輪齒面這種復雜曲面的測量過程中，并不能做到實際加工齒面和理論齒面完全重合。為了減小或消除測量基準不重合誤差及齒距誤差，需要對測頭的實際運動軌跡面進行適當的平移和旋轉等坐標變換，使得變換后的與理論齒面充分吻合［15］。因此，利用參數曲面的幾何不變性，將與He進行曲面匹配后并作比較，得

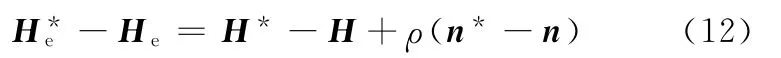
將式（9）代入式（12），得

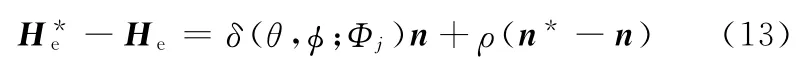
式（13）兩邊與法矢n作點積，得

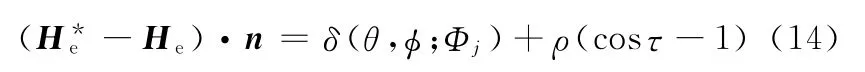
式（14）可寫為

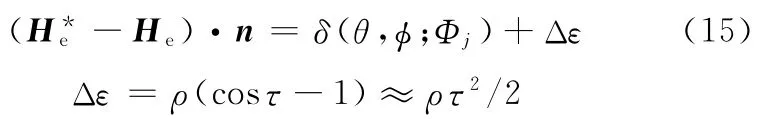
可以看出，Δε是關于ρ和τ的函數，而τ則與齒面誤差δ有直接聯系，δ越大，法線方向n＊和n的空間夾角τ越大。例如，測頭直徑ρ＝1.0mm，τ＝1′，則Δε＝0.14μm。由此可見，如果ρ或τ較大，Δε就是測量中的一項重要誤差源。因此，采用小直徑測頭是減小測量誤差的重要手段。

一般情況下，Δε較小，甚至可以忽略不計。忽略Δε則有

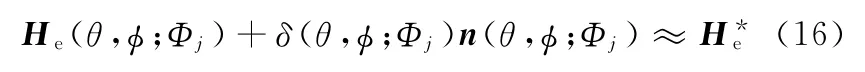
將式（4）代入式（16）整理得

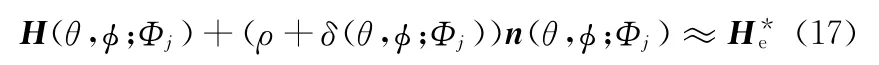
由于測頭直徑ρ和機床運動參數Φj為已知量，測頭實際軌跡面由齒面測量后進行曲面擬合得到，理論齒面H 和法矢n經理論計算確定。因此，式（17）是一個以δ、θ和φ為變量的非線性方程組，優化迭代求解即可得到真實齒面誤差。同樣，如果需要進行齒面誤差修正，則δ為已知量，以Φj、θ和φ為變量進行優化迭代，尋求最佳機床參數Φ＊使得δ趨于最小即可。由此可見，式（17）體現了齒面誤差計算與齒面修正的可逆求解過程，反映了齒面偏差δ與曲面參數θ、φ和機床運動參數Φj之間的映射關系。

4 實驗驗證

以一對汽車后橋齒輪為例來驗證其齒面誤差分析與精確計算的正確性與有效性。齒輪幾何參數如表1所示。被加工大輪在一次裝夾中用雙面刀盤同時銑削凹面和凸面；被加工小輪輪齒的凹面和凸面采用不同刀盤、不同機床運動參數分別加工。通過給定初始展成位置及插補步長，并結合測量齒面的數字化處理，即可得到展成時各聯動數控軸的瞬時運動軌跡位置，如表2所示。

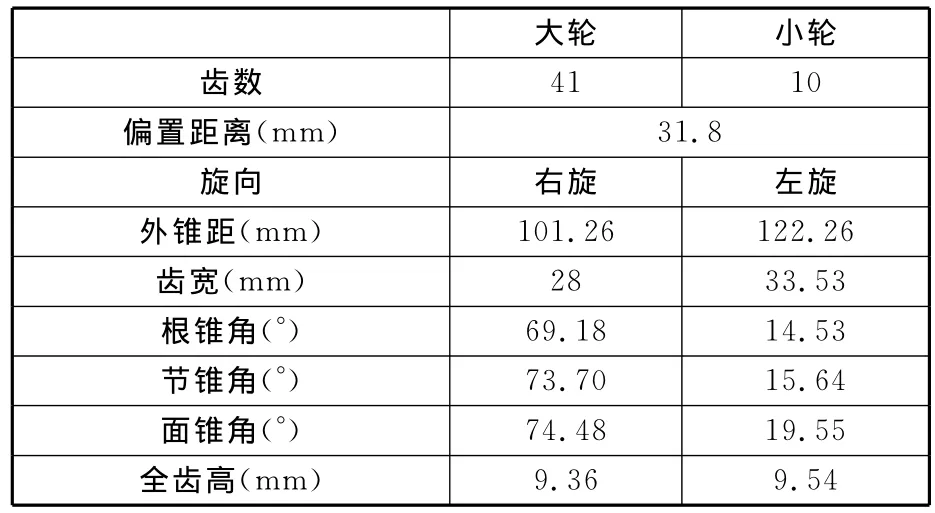
表1 齒輪幾何參數

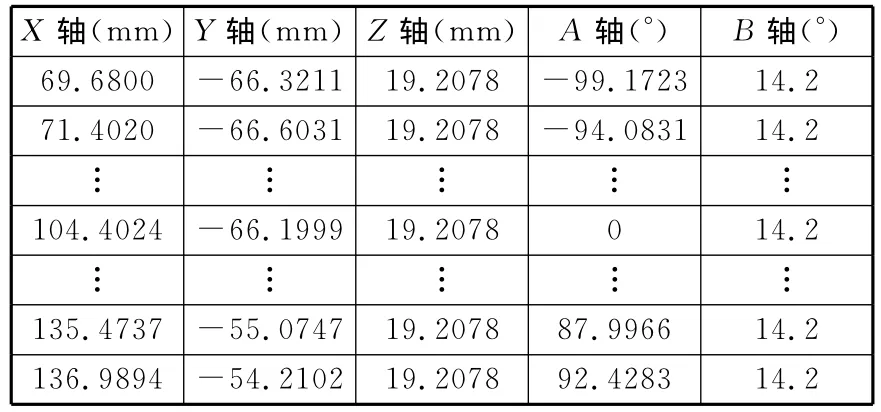
表2 機床運動參數

根據齒面展成與檢測的運動關系分析及測量模型，首先建立理論齒面及法矢方程，見式（1）。運用空間坐標轉換技術，進行理論齒面H的數字化處理；選取測頭直徑ρ＝1.5mm作測頭半徑補償處理，并根據式（4）得到齒面檢測所必需的測頭理論運動軌跡坐標；基于此坐標，采取點陣式接觸測量方法（圖3），測量定位基準面選取與設計基準一致，在JD45＋型齒輪測量中心上對試切后的小輪進行實際齒面檢測，獲取測頭實際運動軌跡坐標

采用JD45＋型齒輪測量中心檢測數據來驗證本文計算方法和實驗結果的有效性，該儀器的精度——齒形示值誤差、齒向示值誤差以及儀器示值變動性（重復性精度）分別 為 1.6μm、1.7μm 和0.6μm，符 合 國 家 標 準GB／T 22097－2008和企業標準 Q／HAD 001－2010。齒面檢測及規劃流程分別如圖5和圖6所示。

圖5 齒面誤差測量

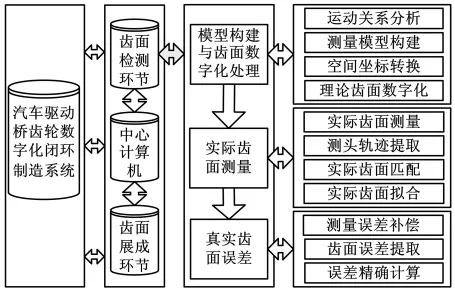
圖6 齒面誤差計算流程規劃

嚴格來講，實際齒面檢測后得到的是測頭中心的實際軌跡，因此實際加工齒面H＊的確定可以通過測頭半徑的第二次補償處理得到；另外，由于汽車齒輪的特殊性和復雜性，為確保齒面數據處理及修正的準確性，需要根據加工和檢測中的角位移θ，利用微分幾何原理進行坐標轉換，使得整個輪齒面處于測量前的初始位置，然后運用優化方法進行齒面的最佳匹配來補償輪坯安裝誤差、齒面定位誤差及隨機性誤差對測量結果的影響；最后進行實際齒面重構得到測頭實際軌跡面此時，測頭直徑ρ、機床運動參數Φj、測頭實際軌跡表達理論齒面H及法矢n均完全確定，進行測量誤差補償處理后并利用非線性方程式（17）即可精確計算齒面誤差值，如圖7所示。由齒面誤差分析可知，齒面誤差越大，則法矢n＊與n空間夾角τ越大。為了確定測量誤差對齒面誤差計算的影響大小，筆者提取了程序運行的中間變量，得到齒面誤差δ＝0.1900mm處的法矢n＊與 n 的 夾 角τ ＝0.025°，得 到 Δε ＝0.47μm。可見，測量誤差對精確計算齒面誤差產生了一定的影響，需要進行補償處理以確保計算誤差的真實性。

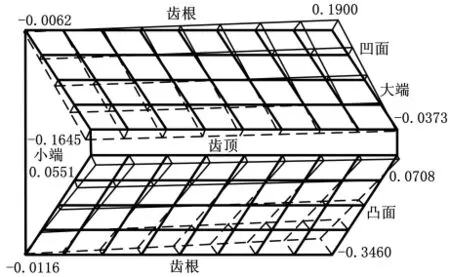
圖7 JD45＋型測量中心上檢測的小輪齒面測量誤差（單位：mm）

為了驗證齒面誤差計算方法的正確性并提高實驗結果的可比性，在使用三維測頭的 M＆M 3525測量中心上對同一輪坯的同一齒面也進行了測量，測量結果如圖8所示。

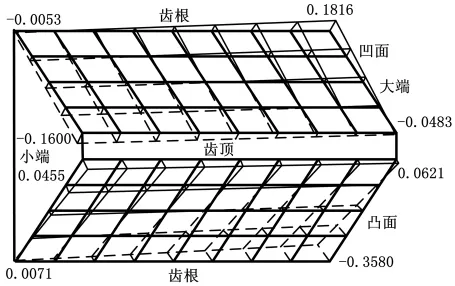
圖8 M＆M 3525型測量中心上檢測的小輪齒面測量誤差（單位：mm）

由圖7和圖8的齒面誤差拓撲圖可以看到，JD45＋型測量中心上測得的小齒面測量誤差的總體趨勢和M＆M3525型測量中心上測量結果保持一致，從而說明了所構建的測量模型和齒面誤差計算方法的正確性。從圖中還可以看到，齒面誤差最大差值在0.01mm以內。究其原因大致有：①三維測頭與一維測頭的工作原理、測量方法以及在齒面檢測過程中對法線方向和測球接觸位置等測量誤差的補償處理不同，使得測量數值存在微小差異；②測量過程中測量參考點的選取位置、測量區域大小及定位基準等因素可能導致差異；③測頭的球度也是影響測量結果重復性和準確性的重要因素之一。

為了更充分地驗證誤差計算方法的正確性，對配對的大輪也進行了齒面加工和測量，具體過程與小輪類似，測量結果如圖9和圖10所示。可以看到，大輪測量結果也是一致的，充分表明該模型和計算方法是正確有效的。

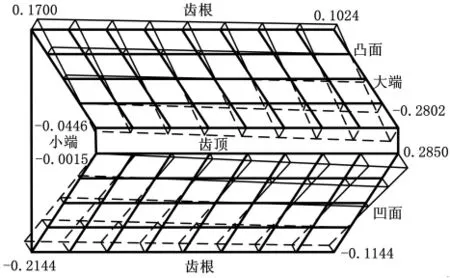
圖9 JD45＋型測量中心上檢測的大輪齒面測量誤差（單位：mm）

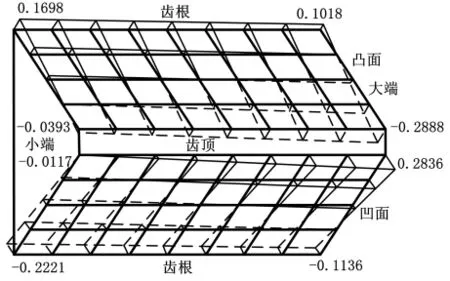
圖10 M＆M 3525型測量中心上檢測的大輪齒面測量誤差（單位：mm）

5 結語

汽車驅動橋齒輪加工測量實驗的結果表明本文所提出的齒面誤差精確計算方法是切實可行的，同時在汽車齒輪生產中大量的實際應用也證明了該方法的實用性和正確性。該方法不僅為汽車驅動橋齒輪的齒面精度改善及數字化閉環制造生產線的順利實施提供了技術支持，同時也為國內高品質的奧利康汽車齒輪制造提供了有價值的參考。

［1］ 汪中厚，周曉玲.汽車驅動橋錐齒輪齒面檢測與質量控制［J］.現代零部件，2005（11）：57－61.

［2］ 曾韜.汽車后橋螺旋錐齒輪制造的發展方向與對策［J］.世界制造技術與裝備市場，2006（6）：79－83.

［3］ 石照耀，張萬年，林家春.小模數齒輪測量：現狀與趨勢［J］.北京工業大學學報，2008，34（2）：113－119.

［4］ 石照耀，費業泰，謝華錕.齒輪測量技術100年—回顧與展望［J］.中國工程科學，2003，5（9）：13－17.

［5］ 劉慧玲，于水琴，曾韜.數字化閉環加工系統在螺旋錐齒輪制造中的應用［J］.機械工程師，2008（4）：103－105.

［6］ 郭曉東，張明德，張衛青，等.錐齒輪齒距及齒形偏差測量與分析方法［J］.工具技術，2009，43（11）：80－83.

［7］ 讓·德福，樊奇.格里森專家制造系統（GEMS）開創弧齒錐齒輪及雙曲面齒輪數字化制造新紀元［J］.世界制造技術與裝備市場，2005（4）：87－93.

［8］ Tobisawa K，Kano M，Saiki K，et al.Real Tooth Contact Analysis of Loaded Hypoid Gear Directly Using Measured Tooth Surfaces［J］.Review of Automotive Engineering，2006，27（2）：317－324.

［9］ Litvin F L，Zhang Y，Kieffer J，et al.Identification and Minimization of Deviations of Real Gear Tooth Surfaces［J］.Journal of Mechanical Design，ASME，1991，113（1）：55－62.

［10］ Litvin F L，Kuan C，Wang J C，et al.Minimization of Deviations of Gear Real Tooth Surfaces Determined by Coordinate Measurements［J］.Journal of Mechanical Design，ASME，1993，115（4）：995－1001.

［11］ 李天興，鄧效忠，魏冰陽.基于一維測頭準雙曲面齒輪齒面偏差的測量［J］.中國機械工程，2007，18（8）：958－962.

［12］ 曾韜.螺旋錐齒輪設計與加工［M］.哈爾濱：哈爾濱工業大學出版社，1989.

［13］ Litvin F L，Fuentes A.Gear Geometry and Applied Theory［M］.Cambridge：Cambridge University Press，2004.

［14］ 曹雪梅，王軍，張海英.弧齒錐齒輪齒面誤差檢測與 實 驗 驗 證 ［J］.中 國 機 械 工 程，2009，20（15）：1799－1801.

［15］ 石照耀，謝華錕，費業泰.復雜曲面測量模式與關鍵技術［J］.工具技術，2000，34（11）：31－34.