熱聲理論的研究進展

吳 鋒, 李 青, 郭方中，舒安慶

(1.武漢工程大學理學院，湖北 武漢 430074；2.中國科學院理化技術研究所，北京 100190；3. 華中科技大學能源與動力工程學院，湖北 武漢 430074)

0 引 言

熱聲系統是一個非常奇妙的能產生熱聲效應的系統，它既簡單又復雜.說它簡單，是因為系統中只是波(駐波、行波或混合波)在運行；說它復雜，是因為它的啟振模態、運行機理以及非線性行為等等仍有許多未解之迷.

所謂熱聲效應[1-3]，是在一定條件下，熱能與聲能相互轉換的現象.它是系統第一介質(可壓縮流體)的聲振蕩與第二介質(固體壁)之間由于熱相互作用而產生的時均能量效應.廣義的說，它是振蕩過程與擴散過程的相互作用與耦合；狹義的說，它是熱能與有序聲能的直接轉換.

1777年，Byron Higgins 最早記載了熱聲現象.在一根兩端開口大管中的適當位置放置燃燒著的氫火焰，可以激發出風琴管的聲音，被稱為“歌焰”.而對熱聲現象的系統研究則始于19世紀，但是直到近幾十年才取得突破性進展[4-6].熱聲熱機(制冷機)就是利用熱聲效應的能量裝換裝置.它最突出的特點是無運動部件，這一特點徹底改變了人們對動力機械的傳統觀念.熱聲熱機(制冷機)由于其結構簡單、壽命長、無污染、無運動部件、可利用太陽能及其它低品位能源等諸多優點而倍受動力工程領域和低溫工程領域的青睞.美國于20世紀70年代中開始研究熱聲熱機(制冷機)，日本于80年代末跟進.現在美國、日本等國都已開始應用研究階段.我國于60年代開始軍用斯特林制冷機研制，90年代初開始立項進行熱聲原理研究.在21世紀初，我國的小冷量、長壽命自由活塞斯特林制冷機已開始在航天器上試用，熱聲諧振管的研究也獲得很大進展，一些新的熱聲熱機和熱聲制冷機的實驗裝置不斷出現[7-8].

對熱聲理論的研究是從對熱聲回熱器的研究開始的.常用的理論有“定常流模型”、“交變流動模型”、“相移模型”、“線性熱聲模型”、“短板邊界層近似模型”、 網絡模型、非線性熱聲理論[9]等，常用的計算方法有Delta-E 程序[10]、CFD模擬[11-13]、格子氣自動機模型[14-15]等.本文擬對熱聲理論相關方面的研究狀況做一簡要介紹.

1 網絡模型

在對斯特林熱機回熱器的研究中，華中科技大學郭方中[16-18]教授的研究小組首次提出了等溫回熱器的網絡模型，運用流體網絡阻、感、容等概念以及熱動力學理論和網絡方法分析研究了回熱器中流體的流動特性.中科院低溫中心的肖家華[19-21]根據固體壁面與外熱源的熱接觸情況將熱聲效應劃分為“等溫熱聲效應”、“絕熱熱聲效應”和“一般情形熱聲效應”三種情況.肖家華提出了等溫熱聲效應和絕熱熱聲效應的物理模型并建立了對應的波動方程，構建了回熱式制冷裝置相關熱聲理論的定性框架，在國際上最早將熱聲理論應用于回熱器的研究工作中.鄧曉輝[22]通過引入熱聲“源”，建立了非等溫回熱器的網絡模型，為網絡模型在熱聲系統中的具體應用奠定了堅實的基礎.張曉青[23]建立了熱聲熱機系統集總參數網絡模型，研制設計出一種熱聲網絡計算軟件TANketwork.涂虬[24]采用熱動力學與聲學理論相結合的研究方法，建立了熱聲回熱器分布參數網絡模型，并用聲傳播常數和特性阻抗等來表述模型中的聲學參數.胡興華等[25]將熱聲系統視為由主動網絡與被動網絡組成的熱聲振蕩器，采用“負阻”和“反饋”分別建立了駐波和行波熱聲發動機的網絡模型，研究了二端口駐波和行波網絡的拓撲結構，并利用Nyquist穩定性判據得到了熱聲振蕩器的起振或運行條件.

網絡模型是熱聲熱機工程研究的強有力的工具，它可以把熱聲熱機(制冷機)系統各部件有機的聯立起來.李青[26]建立了分置式斯特林制冷機整機網絡模型，董凱軍[27]、涂虬[28]、鄒文徑[29]對熱聲系統各部件以及整機的網絡進行了描述.在熱聲系統網絡模型的研究中，關鍵環節之一是量化網絡，即確定網絡各矩陣元的值.量化網絡參數的有效方法是辨識.吳鋒[30]、丁國忠[31]等以毛細管數作為辨識參數，對網絡的H矩陣進行了系統辨識，張春萍[32]等利用實驗辨識方法，對熱聲回熱器的復流容進行了研究.

目前，網絡模型研究的最新進展是將辛群理論用于熱聲網絡中，探索熱聲系統的辛對稱特征.通過對熱聲系統網絡傳輸矩陣的分析，楊志春[33，34]證明了系統中等溫流體管道內工質運動的傳輸矩陣為辛矩陣，而存在溫度梯度的熱聲回熱器中氣體工質微團的傳輸矩陣可以通過變量代換，將傳輸矩陣轉換為辛矩陣，使整個熱聲系統網絡傳輸都可用辛矩陣傳輸來表示.

在辛數學中，辛對稱是一種“糾結”(entanglement)對稱，例如電和磁是一對“糾結”.有待進一步研究的問題是：既然熱聲系統可以用辛矩陣來表示，那么，聲和熱是否也是一對糾結？熱聲中的勢和流呢？在熱聲中，頻率ω與特征時間τ的乘積是一個很重要的參數，它們可能也是一對糾結，理想回熱器ωτ=1，“糾結”沒有了，于是要靠機械來調節相位.但熱聲疊使ωτ≠1，于是時(τ)與空(ω)得以借助諧振使無序的“熱”在溫差偏置的作用下成為有序的“聲”.因此同樣值得思考的是，時與空是否也是一對“糾結”呢？

辛數學的引入，不但可以加深對熱聲網絡模型物理意義的理解，而且可以將辛群的計算方法直接應用于熱聲系統網絡模型，從而對復雜熱聲網絡的計算起到促進作用.

2 參數諧振

物質以各種運動形態向人們展現著它的存在和演化，呈現出大自然的五彩繽紛和驚人魅力.“自激振蕩”就是一種奇妙的自然現象.電路中的電和磁自激振蕩，化學波中的化學振蕩，紅旗迎風飛舞，自來水管的遄流聲等都是常見的自激振蕩.自激振蕩有三個基本特點[35]：一是系統的自激振蕩與初始條件無關，只取決于系統的內稟性質；二是自激振蕩必定伴隨有能量耗散，外界必須給系統泵入能量才能維持系統振蕩；三是自激振蕩系統是一個自治系統.熱聲振蕩不是強迫振蕩，這是因為系統并不受周期性外力作用，而是來源于系統的非線性性質.為了維持自激振蕩，系統需要有能源以補償耗散，但它并不需要外加的激振源，而是靠系統的特性將能源調制成為頻率為ω的振蕩，所以供給的能源可以是非時變的恒定值，系統具有將得到的能量調制成周期性的能力.對于一個熱聲系統，雖然其運行機理仍在探索之中，但其自激振蕩的實質已無非議.自激振蕩系統的關鍵部件是所謂的非線性環節.例如，所有的熱機都利用工質的熱脹冷縮(即體積隨溫度的非線性變化)來形成偏置反饋特性，它和系統的流感、流容、流阻聯合起來，組成各種不同的非線性環節.熱聲熱機的非線性環節就是熱聲回熱器(熱聲疊).熱聲系統的這種非線性環節構成了它的一個顯著特點，不需要任何可動的機械組件就可實現能量轉換.

沿熱聲回熱器多孔填料行進的聲波與回熱器的溫度梯度同相，就會使聲功流加大，這個過程所用的是上一周循環儲存在填料中的熱量，它通過使流相工質加熱膨脹，把放大了的聲功正反饋給回熱器子系統，使它成為一個有源的器件.這個正反饋關系使回熱器成為斯特林熱機和熱聲熱機的非線性環節.它使熱聲系統能用環境所提供的“溫差”(溫度梯度)激發持續的熱聲振蕩形成熱聲循環.在電子器件中，放大電路的基極偏置電位能使集電極電流被放大.以此類似，熱聲系統的“溫差”就使聲諧振管中的聲流得到放大.

為解釋熱聲系統自激振蕩的機理，一些研究者提出了參數諧振理論[32，35，36].在電路中，通過周期性的改變電容值從而實現能量增益方式被稱為“泵送”，也稱參數激勵.熱聲回熱器內流體工質和其它熱力學系統一樣，總是充滿著熱力學起伏.正如我們大家都知道的那樣，這種熱力學起伏是頻帶很寬的噪聲，系統的本征頻率(系統任意一個本征頻率用ωi表示)必定存在于其中.顯然，具有本征頻率的振蕩分量出現的概率與其它頻率的振蕩分量出現的概率一樣.如果外界對系統持續輸入簡諧能量，且系統的本征頻率ωi和振蕩頻率ωp恰好滿足ωi=nωp/2(n=1,2,3,…)的關系時，系統將產生參數諧振.

既然熱聲系統的非線性流容可以作為系統自激振蕩的參數激勵，那么用三頻率參數網絡模型來描述一個熱聲諧振管系統就是順理成章的了.熱驅動的熱聲諧振管回熱器子系統由三個不同本征頻率的振蕩回路耦合而成[36].第一是頻率為本征聲頻率ω0的LC回路，它是諧振管所造成的縱向聲振蕩，可在回熱器中調制出橫向熵波；第二是熱聲振蕩回路，它是熵波調制過程在回熱器LC回路中所激發的，其頻率為取決于回熱器填料孔隙度、流道形狀及兩端溫差的回熱器本征頻率ωTA；第三是熱端換熱器所提供的熱聲發射譜中與本征聲頻ω0成整數(或分數)倍關系的諸頻段ωi.這三個頻率的合理耦合就構成了三頻率參數的網絡，可以使系統獲得壓力波幅最大的熱聲振蕩聲功流.Sugita[37]等報告的熱聲諧振管系統就是一種工作于自激振蕩的三頻率參數熱聲系統.它包括回熱器、諧振管和變容諧振腔兩個子系統，其中回熱器子系統的本征頻率是24.4Hz，諧振管和變容諧振腔的本征頻率是9.5 Hz，而整機輸出的聲功頻率范圍則是30.3～33.8 Hz.

熱聲自激振蕩和參數諧振是一個比較引人入勝的課題.凡是用周期地改變網絡無源參數的方法使非線性的負阻元件與諧振儲能元件形成正反饋的振蕩系統，讓它維持定常的自激振蕩，就稱為參數激勵.這種自激振蕩方法已經成功地用于電子技術和激光技術.既然有受激電磁幅射振蕩造成的光放大即激光，那么是否也可以有受激熱聲振蕩的聲放大？

3 特征時間

理論和實驗研究都表明，熱聲系統對特征時間的響應非常敏感[32，35].Zuber等[38]把時間變量引入包括信息量在內的熱力學系統的研究中.信息量是負熵，而熵是熱力學參數中的廣延量.從熱動力學觀點來看，ω是表征熱力學系統傳輸過程強度的時間尺度.Zuber等人的研究策略是用系統信息流程的熱力學過程方向(縱向)特征時間ω(相對時變率)和對環境開放的傳輸(橫向)特征時間τ的對比值ωτ來表征整個熱機系統的能量轉換效應.

對特征時間的研究，最有效的方法之一就是所謂的“時變率相似分析”. 熱機系統進行能量轉換的體積V是一個信息傳輸體積，它的表面積A是系統與環境交換質量、能量與信息的傳輸界面.描述系統經歷弛豫過程達到新的平衡的特征參數是λ=A/V.具有長度量綱的1/λ是宏觀系統的特征尺寸.傳輸界面A上所進行的環境與系統間的任何傳輸都是對系統的擾動而導致系統的響應.對這些響應，系統需要經歷弛豫過程才能達到新的平衡，它所經歷的時間就是弛豫時間.

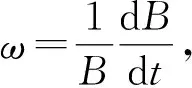
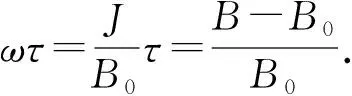
熱機系統有三個層次：宏觀、介觀和微觀.熱聲熱機橫向傳輸過程的特征尺寸是流體微團尺寸，它發生在受熱區子系統，屬于介觀層次；而其耗散過程應屬于微觀層次，此層次的特征時間τs可以通過系統動量變化的特征時間ωs(可測值)辨識出來.在此基礎之上，就可以確立宏觀的橫向傳輸的熱動力學相似關系.在宏觀層次上，這種熱動力學相似關系受幾何結構因素影響很大，因此必須提高研究層次，即深入到介觀層次及微觀層次，以便收集更多信息.介觀層次的特征尺寸是過程影響所及的微團尺寸，相應地有過程位移ξp和特征尺寸τp，由此可得相對效應量Ωp，即無量綱特征時間.在微觀層次，耗散過程是分子隨機行走所引起的擴散過程，描述參數是流動位移ξf，過程的模型已被還原為經典熱力學.我們可以通過所得到的介觀層次傳輸過程效應量Ωp=ωmpτp，辨識出微觀層次中耗散過程的特征量ωk，λk和τk，從而得到微觀層次的過程效應.

綜上所述，在熱聲自激振蕩系統中，可以把ω0τTA(ω0是聲系統本征頻率，τTA是橫向熵波弛豫時間)作為系統的熱聲特征時間(無量綱)，它決定回熱器(熱聲疊)的特征尺寸即侵入層厚度δ和諧振管的長度，因此是一個重要的設計參數.

4 熱力學優化

有限時間熱力學也稱“熱力學優化”，是現代熱力學理論的一個新的分支，是研究在有限時間內發生的帶有熱現象的過程的最優效果，在有限時間內運行的帶有熱現象的裝置和系統的最優性能的一門科學.

熱聲系統是一個開放的系統，利用有限時間熱力學對熱聲系統進行研究已取得一定的成果[39].武漢工程大學熱聲課題研究小組利用有限時間熱力學對熱聲系統的自激振蕩機理[40]、生態學優化性能[41]、火用效率優化[42]、回熱器熵產[43]、最優頻率特性[44]等進行了深入的研究.

在有限時間熱力學的研究中，非平衡量子統計理論是揭示開放系統不可逆本質規律的一個強有力的工具.吳鋒等[45]把非平衡量子統計理論引入到對熱聲微熱力學循環的研究中，認為熱聲系統氣體工質由熱聲子組成，建立了理想玻色系統的熱聲微熱力學循環，研究了量子熱聲微熱力學循環的最優性能.結果表明[39]：在弱簡并條件下，熱聲原動機量子微熱力學循環的輸出功率大于經典熱力學循環的輸出功率，熱聲制冷量子微熱力學循環的制冷率大于經典熱聲微熱力學循環的制冷率；在經典極限條件下，量子熱聲系統微熱力學循環回到經典的熱聲微熱力學循環.

目前有限時間熱力學進展較大的方面是所謂的“構型優化”. “構型”是相對于“分形”逆向思維的結果.自古到今，人們對自然界存在的各種形狀都感到好奇.為什么植物的葉子有經絡？為什么花兒有不同的花瓣？為什么魚兒具有流線型？等等.如何設計出合理的過程和結構，從而獲得最佳目標值，這就是構形理論.吳鋒等[46]根據構型理論對駐波型熱聲疊進行了優化設計，得到了一些有用的結果.他們的工作目前僅僅限于一級優化，根據推測，二級優化的聲通道應當是方型，三級、四級優化將會是什么結果呢？這些問題都有待于下一步的工作進展.

5 格子氣模擬和非線性熱聲理論

格子氣方法是20世紀80年代發展起來的現代熱流體計算方法，已經在兩相流、傳熱、聲波[47]等領域得到具體應用.直接從微觀角度和基本物理定律出發來模擬系統的物理過程是格子氣方法的最大優點.采用格子氣算法不用建立和求解復雜的微分方程，而且算法簡單并容易處理邊界條件和使用并行算法.在熱聲的研究中，可以從格子氣自動機演化方程恢復宏觀熱聲方程，從而采用相應熱格子氣模型模擬熱聲熱機系統的壓力場、溫度場和速度場[47].

隨著熱聲研究的深入，經典熱聲理論的局限性日顯突出.特別是熱聲系統的起振、聲流、諧波耗散等非線性現象，經典熱聲理論無法解釋.人們逐步認識到非線性效應才是時均非零熱能與聲能轉換的本質，而線性熱聲理論在小振幅條件下的預測只是一種近似.于是，自20世紀90年代初開始興起了對非線性熱聲理論的研究.

1992年，美國Los Alamos實驗室研究人員[48]在研究大尺度熱聲發動機時，定性解釋了他們所發現的一些與線性熱聲理論相背的現象.Gusev[49]通過建立非線性演化方程來描述熱聲發動機起振過程，并得到了對熱聲板疊頻譜特性的解析描述.Karpov S 等[50]建立了一個時域的、完全非線性的熱聲模型，并對其非線性行為進行了較為系統的研究.他們通過改變橫截面積、板疊位置和流體性質等參數，預測了熱聲系統的變化規律.他們的理論可以在小振幅情況下簡化為N.Rott的線性理論.Hamilton等[51]用攝動方法獲得了系統本征頻率的漸進表達式，建立了研究非線性熱聲效應的二維模型和數值方法.最近幾年，國內一些學者對非線性熱聲理論也進行了較為深入的研究[52].

6 展 望

熱聲熱機(制冷機)用熱聲諧振取代機械壓縮，使得熱機(制冷機)有可能變成無運動部件的換能器，熱功轉換過程的頻率大大提高，能源技術將有一個質的飛躍.熱聲裝置的工程研究分別沿著兩個方向發展.一是高頻率小型化，其重量和尺寸將主要取決于微機械加工工藝(MEMS)的水平；二是大振幅行波熱聲與熱氣機相結合，構建大型能量轉換平臺.為深入探尋熱聲機理，促進學科發展，以及為熱聲裝置的設計、調相、運行參數選擇等提供指導，未來幾年可能會在如下幾個方面形成理論研究的熱點.

a.熱聲自激振蕩來源于系統的非線性特征.隨著各種結構的高頻大振幅熱聲裝置的不斷推出，非線性熱聲理論必將成為研究重點之一，構建一個描述熱聲系統的非線性動力學理論并形成與之相應的計算方法勢在必行.

b.以時變率相似分析方法為基礎，把特征時間作為評價熱聲系統性能的重要指標來深入研究.在熱聲裝置的啟振或運行過程中，系統的特征時間起著何種作用？是否存在最優的特征時間？這些都需要在理論和實驗兩個方面來嘗試或探尋.

c.采用“相空間重構”、“時序分析”、“網絡分析”、“有限時間熱力學”等綜合分析方法，利用Delta-EC、CFD、格子氣等計算程序，對各種熱聲系統進行動態分析和模擬.

d.把熱聲系統作為大自然復雜系統的自組織歷程的一部分，利用復雜系統的形態(Pattern)動力學觀點，來揭示熱聲自激振蕩的本質，從而促進工程熱物理學科的發展；結合道家哲學來探究熱聲耦合的自然本源，例如，道家的“剛”對應熱聲中的“流感”，道家的“柔”對應熱聲中的“流容”，而“剛柔相濟”顯然就是“諧振”.

熱聲學是一門跨學科的科學，無論是理論研究還是工程化研究都極具挑戰性.它像一個極具生命潛質，又帶有眾多疑問的魔夾，以它特有的魅力吸引著人們不斷地探索和研究.

參考文獻：

[1] Rott N. Damped and thermally driven acoustic oscilla-

tions in wide and narrow tubes [J]. Z Angew Math Phys, 1969(20): 230.

[2] Rott N. Thermoacoustic [J]. Adv Appl Mech, 1988(20): 135-175.

[3] Swift G W. Thermoacoustic engine [J]. J Acoust Soc Am, 1988, 84(4): 1145-1180.

[4] Wheatley J C, Cox A. Natural engines[J]. Physics Today, 1985(38): 50.

[5] Olson JR, Swift G W. A loaded thermoacoustic engine[J]. J Acoust Soc Am, 1995, 98(5): 2690-2693.

[6] Backhaus S, Swift GW. A thermoacoustic-Stirling heat engine[J]. Nature, 1999(399): 335-338.

[7] 周遠, 羅二倉. 熱聲熱機技術的研究進展[J]. 機械工程學報, 2009, 45(3): 14-26.

[8] 趙忠明，李青，胡忠軍. 熱聲機械的研究現狀及展望[J]. 流體機械，2009，37(4)：79-82.

[9] Km'pov S,Prosperetti A. Nonlinear saturation of the thermoaconstic instability[J]. J Aconst Soc Am, 2000, 103: 3130-3147.

[10] Ward W C, Swift G W. Design environment for low amplitude thermoacoustic engines (DeltaE) [J]. J Acoust Soc Am, 1994, 95(6): 3671-3672.

[11] 余國瑤, 羅二倉, 胡劍英, 等. 熱聲斯特林發動機熱動力學特性的CFD研究——第一部分: 熱聲自激振蕩演化過程[J]. 低溫工程, 2006(4): 5-9.

[12] Florian Z, Jeffrey V, Laura S. CFD simulation of thermoacoustic cooling [J] International Journal of Heat and Mass Transfer, 2010(53): 3940-3946.

[13] 王軍. 熱聲部件聲特性的數值模擬研究[D]. 武漢：武漢工程大學，2010.

[14] 張曉青, 蔣華, 胡興華, 等. 熱聲振蕩的格子氣模擬[J]. 華中科技大學學報：自然科學版, 2007, 35(7): 85-88.

[15] 張曉青，吳迎文，張穩. 熱聲熱機聲場的格子氣分析[J].工程熱物理學報, 2010, 31(2): 185-188.

[16] GUO Fang Zhong. On the theory of cyclic flow cryogenic regenerator [C]//Proc Of INCONCRYO India, 1985: 227.

[17] GUO Fang Zhong, Chouym, Lee S Z. Flow characteristics of a cyclic flow regenerator [J]. Cryogenics, 1987(27): 152.

[18] 陳國邦. 最新低溫制冷技術[M]. 北京：機械工業出版社，1994.

[19] XIAO Jia Hua. Thermoacoustic theory for cyclic flow regenerators Part 1: Fundamentals [J]. Cryogenics, 1992, 32(10): 895-901.

[20] XIAO Jia Hua. Thermoacoustic heat transportation and energy transformation Part 1: Formulation of the problem [J]. Cryogenics, 1995, 35(1): 15-19.

[21] XIAO Jia Hua. Thermoacoustic heat transportation and energy transformation Part 3: Adiabatic wall thermoacoustic effects [J]. Cryogenics, 1995, 35(1): 27-29.

[22] 鄧曉輝. 回熱器的熱聲機理及熱聲熱機的設計理論[D]. 武漢：華中科技大學， 1994.

[23] 張曉青. 熱聲熱機系統的仿真與優化研究—仿真軟件的研制與實驗驗證[D]. 武漢: 華中科技大學, 2001.

[24] TU Qiu, Wu C, LI Qing, et al. Influence of Temperature Gradient on Acoustic Characteristic Parameters of Stack in TAE [J]. International Journal of Engineering Science, 2003(41): 1338-1349.

[25] 胡興華, 張曉青, 王惠齡, 等. 熱聲振蕩器的二端口網絡模型及起振條件[J]. 科學通報, 2008, 53(17): 2109-2115.

[26] 李青. 低溫動力機械的研制—熱機研制的系統動力學方法[D]. 武漢: 華中科技大學, 1996.

[27] 董凱軍. 熱聲系統的網絡模擬及其實驗研究[D]. 武漢: 華中科技大學, 2000.

[28] 涂虬. 熱聲器件的尋優及其與熱聲熱機系統的匹配[D]. 武漢: 華中科技大學, 2003.

[29] Zou Wenjing, Wu Feng, Shu Anqing, et al. Study on a new traveling wave thermoacoustic engine with external excitation[J]. Asia-Pacific Power and Energy Engineering Conference, 2009，3: 2555-2558.

[30] 吳鋒,郭方中，李端勇. 熱聲回熱器有源網絡的系統辨識. 應用科學學報[J]，2001，19(4)：67—69.

[31] DING Guozhong. An Identified Study on the Active Network of a Thermoacoustic Regenerator[J]. Engineering, 2009, 1, 1-54.

[32] 張春萍. 熱聲核特性參數實驗研究及高頻微型熱聲實驗裝置的研制[D]. 武漢: 華中科技大學, 2011.

[33] 楊志春，吳鋒，郭方中，等. 熱聲網絡的辛對稱特征[J]. 物理學報，2011，60(8)：084303.

[34] 楊志春. 熱聲系統網絡傳輸矩陣的理論和實驗研究[D]. 武漢: 海軍工程大學, 2011.

[35] 郭方中，李青. 熱動力學[M]. 武漢: 華中科技大學出版社, 2007.

[36] 陳熙. 熱聲諧振管參數激勵機理研究—整機動態特性與回熱器熱致聲諧振模態識別[D]. 武漢: 華中科技大學, 2004.

[37] Suigata H, Matsubara Y, Kushino A, et al. Experimental study on thermally actuated pressure wave generator for space cryocooler[J]. Cryogenics, 2004, 44:431-437.

[38] Zuber N.The effects of complexity, of simplicity and of scaling in thermal-hydraulics[J]. Nuclear Engineering and Design, 2001, 204: 1-27.

[39] 闞緒獻. 熱聲系統的熱力學分析與優化及外激勵熱聲發動機的研制和實驗研究[D]. 武漢: 海軍工程大學, 2010.

[40] LI Qing, WU Feng, GUO Fang-zhong. Thermodynamic analysis on thermoacoustic self-excited oscillation[J]. Open System and Information Dynamics, 2003, 10(4): 391-402.

[41] Chen Lingen, Wu Feng, Li Qing. Exergetic efficiency optimization of a thermoacoustic cooler[J]. Proceedings IMechE, Part C: Mechanical Engineering Science, 2007, 221(11): 1339-1344.

[42] Xuxian Kan, Feng Wu, Lingen Chen. Exergy efficiency optimization of a thermoacoustic engine with a complex heat transfer exponent[J]. International Journal of Sustainable Energy，2010, 29(4)：220-232.

[43] 余士成，吳鋒. 鋼絲型回熱器的不可逆熵產分析[J]. 吉林大學自然科學學報，1999(3)：52-56.

[44] 闞緒獻，吳鋒. 駐波熱聲熱機的最優頻率特性[J]. 低溫工程, 2008(4)：24-27.

[45] Wu F, Chen L， Li D, et al. Thermodynamic performance on a thermoacoustic micro-cycle under the condition of weak gas degeneracy[J]. Applied Energy，2009，86(7-8)：1119-1123.

[46] Feng Wu, Lingen Chen, Anqing Shu, et al.Constructal Design of Stack filled with parallel plates in Standing-wave Thermo-acoustic Cooler[J]. Cryogenics，2009，49: 107-111.

[47] 王勇，何雅玲，劉迎文，等. 聲波衰減的格子-Boltzmann 方法模擬 [J]. 西安交通大學學報, 2007, 41(1): 5-8.

[48] Swift G W. Analysis and performance of a large thermoacoustic engine [J]. J Acoust Soc Am, 1992, 92(3): 1551-1563.

[49] Guesv V. Asymptotic theory of nonlinear acoustic waves in a thermoacoustic Prime-mover [J]. Acustica, 2000(86): 25-38.

[50] Karpov S, Prosperetti A. A nonlinear model of thermoacoustic devices [J]. J Acoust Soc Am, 2002, 112(4): 1431-1444.

[51] Hamilton M F, Ilinskii Y A, Zabolot skaya E A. Nonlinear two-dimensional model for thermoacoustic engines [J]. J Acoust Soc Am, 2002, 111(5): 2076-2086.

[52] 高凡，劉迎文，何雅玲,等. 熱聲制冷機聲場中非線性效應[J]. 工程熱物理學報, 2008, 29(12): 1990-1992.