高層框架彎曲變形引起的側移與軸向變形引起的側移間的關系
薛明琛
(聊城大學建筑工程學院,山東聊城252059)
框架結構的側向位移主要是由水平荷載引起的,故一般情況下僅進行水平荷載作用下的側移計算。結構的位移由各桿件的彎曲變形、軸向變形和剪切變形引起(不考慮沉降和溫度變化的影響)。框架結構屬于桿系結構,截面尺寸相對其長度比較小,因而可以不考慮剪切變形的影響。因此,框架結構的側向位移由彎曲變形引起的側移和軸向變形引起的側移兩部分組成。
1 由梁柱彎曲變形引起的側移
由梁柱彎曲變形引。起的側移[1]如圖1所示,頂點側移量uM為各層層間側移之和,即

其層間位移:

式中:VFj為水平荷載在j層產(chǎn)生的層間剪力;Djl為第j層第l柱的抗側剛度。
計算層間位移常用的方法有反彎點法、D值法以及門架法。因為對于高層框架結構特別是考慮抗震要求要滿足強柱弱梁的條件,則梁柱的線剛度必定滿足ib/ic<3,此時要考慮桿件兩端的轉角,因此采用D值法。柱的抗側剛度[2]:D=,式中α為柱抗側移剛度修正系數(shù);E為彈性c模量;I為慣性矩;h為柱的計算高度
對于規(guī)則框架,各層框架的抗側剛度大致相等,而層間剪力自下而上逐層增加,因而層間側移自下而上逐層增加,整個結構的變形曲線類似懸臂構件剪切變形引起的位移曲線,因此框架結構的變形曲線稱為“剪切型”(圖1)。

圖1 梁柱彎曲變形
2 由柱軸向變形引起的側移
在水平荷載作用下柱的軸向變形引起的側移[1]如圖2所示,曲線呈“彎曲型”,即類似懸臂構件彎曲變形引起的位移曲線。桿件軸向變形引起的位移計算公式為:

式中:N1為頂點作用單位水平力時在柱子內(nèi)產(chǎn)生的軸力;NF為水平外荷載作用下的柱子軸力;A為柱子的截面面積。

圖2 柱軸向變形
框架在水平荷載作用下,一側的柱子產(chǎn)生軸向拉力,另一側的柱子產(chǎn)生軸向壓力;外側的柱子軸力大,內(nèi)側的柱子軸力小。為簡化,忽略內(nèi)柱的軸力,并近似取外側柱軸力為:

式中:M為上部水平荷載在任一高度產(chǎn)生的力矩;B為外側柱之間的距離。
將節(jié)點水平荷載化為分布荷載q(y),在高度z處,有:

將式(4)代入式(3)可得到柱軸向變形引起的頂點側移,側移與q(y)的形式有關。假定柱截面沿高度不變化,則對于框架受均勻分布水平荷載作用下,框架柱軸向變形引起的頂點側移為:
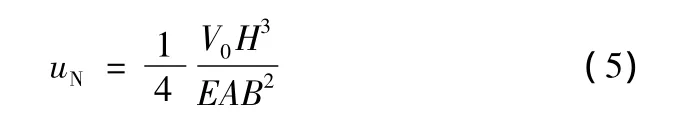
式中:V0為水平外荷載在框架底面產(chǎn)生的總剪力。
3 彎曲變形引起的側移與軸向變形引起的側移間的關系
兩種框架結構(10層~20層),每榀框架均為兩跨,均選取中間一榀框架,尺寸如圖3所示。框架的總寬度分別為:B1=11.4 m,B2=14.8 m,底層層高均為5 m,其余層高均為3.2 m,均采用C40混凝土。兩種框架結構的梁、柱截面尺寸均為:橫梁為250 mm×600 mm;中柱為700 mm×700 mm;邊柱-600 mm×600 mm。所受水平均布荷載標準值:3 kN/m。

圖3 兩種框架結構尺寸
兩種框架結構的總層數(shù)由10層至20層的高度(H)、底部剪力V0(kN)、彎曲變形引起的側移uM(mm)、軸向變形引起的側移uN(mm)以及uN/uM的值如表1和表2所示。uM和uN分別根據(jù)式(1)和式(5)計算得出。通過計算得出的層間移值滿足《建筑抗震設計規(guī)范》(GB 50011-2001)5.5.1要求,即(h為層高)。由軸向變形引起的uN、由彎曲變形引起的uM以及比值uN/uM的對比見圖4~圖6。

表1 B1=11.4 m的框架各項指標

表2 B2=14.8 m的框架各項指標
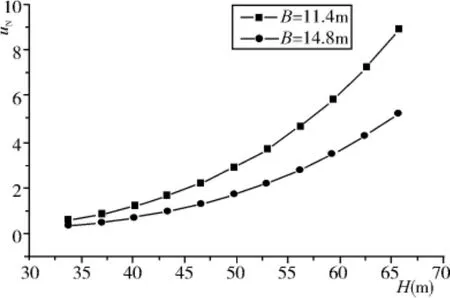
圖4 軸向變形引起的側移值uN

圖5 彎曲變形引起的側移值uM

圖6 軸向變形的側移量與彎曲變形的側移量比值
4 結論
由以上分析可知,隨著結構高度的增加以及結構高寬比的增加,由軸向變形引起的側移值逐步增加且增長的速度越來越快;由彎曲變形引起的側移值隨著高度的增加而增加,隨著高寬比的增加而減少;由軸向變形的側移量與彎曲變形的側移量的比值圖可知,隨著高度的增加,軸向變形所引起的側移值占總側移值的比值越來越大,隨著高寬比的增加,該比值呈增長趨勢。在圖中還可看出,在高寬比選擇合適的情況下,當框架結構高度小于50 m的前提下,由軸向變形引起的側移值與彎曲變形引起的側移值的比值不超過10%,因此,這種情況下可忽略軸向變形引起的側移值。如果框架寬度相對于高度的比值較小,軸向變形所引起的側移值則不能忽略。高度達到什么程度以及高寬比是達到何鄰界值時可忽略軸向變形引起的側移徝還有待于進一步研究。
[1]邱洪興.建筑結構設計[M].北京:高等教育出版社,2007:181-182
[2]沈蒲生.高層建筑結構設計[M].北京:中國建筑工業(yè)出版社,2006:120-121

