界面元法在機械結構結合部問題中的應用

石 坤 宋 俐 師俊平

西安理工大學，西安，710048

0 引言

為了滿足各種功能、性能和加工要求以及便捷運輸，機械裝置一般都是由各種零部件按一定要求裝配起來的組合體，常稱各零部件之間的接觸表面為“機械結合面”，簡稱“結合面”，或“接觸面”。結構中存在的大量結合面使得整個機械在結構上不再是一個連續(xù)的整體，因此分析這類非連續(xù)結構問題會變得復雜和特殊［1］。

機械結合面具有復雜的作用機理——多重因素非線性耦合，以往的大部分研究基本上與試驗相關，如20世紀80年代以伊東誼［2］為代表的日本學者、20世紀90年代以黃玉美等［3］為代表的中國學者均做了大量的典型結合部特性的試驗研究，積累了較為豐富的試驗數據。但是要利用獲得的結合面特性參數的試驗數據對機械進行整體分析，以指導其結構的設計和改型還需要通過數值算法才能實現。目前常用于結構分析的數值方法是有限元法［4－6］，但基于連續(xù)介質力學的有限元法在處理不連續(xù)問題時表現出明顯的局限性。在外載荷作用下，不連續(xù)的結構面往往會產生不同程度的錯動、張開和滑移等不連續(xù)變形，而用有限元法的協(xié)調位移模式是不能模擬這類不連續(xù)變形的，盡管在有限元分析中可以設置各種接觸單元，但這樣做仍然會涉及接觸參數的確定問題，并且在分析中使用過多的接觸單元數也會導致線性方程組出現病態(tài)，使方程組的數值求解不穩(wěn)定甚至不收斂。

本文應用不連續(xù)介質力學的界面元法［7－8］，以螺栓連接的機械結構為研究對象，建立包括結合部特性的機械結構界面元計算模型，通過數值分析得到在各種預應力作用下該結構的變形值，并將其與試驗結果進行比較。此研究旨在探討用界面元法分析機械結構結合部問題的可行性和有效性。

1 界面元法的基本方程

界面元法是在Kawai等［9］提出的剛體－彈簧元模型的基礎上發(fā)展起來的一種求解非均勻不連續(xù)介質的靜動力學問題的數值解法，它仍以虛功原理為基礎，用反映彈、黏、塑等各類變形特性的界面元取代彈簧元，將單元的變形等效在界面上，最終形成以各單元形心的6個位移分量為基本未知量的支配方程。

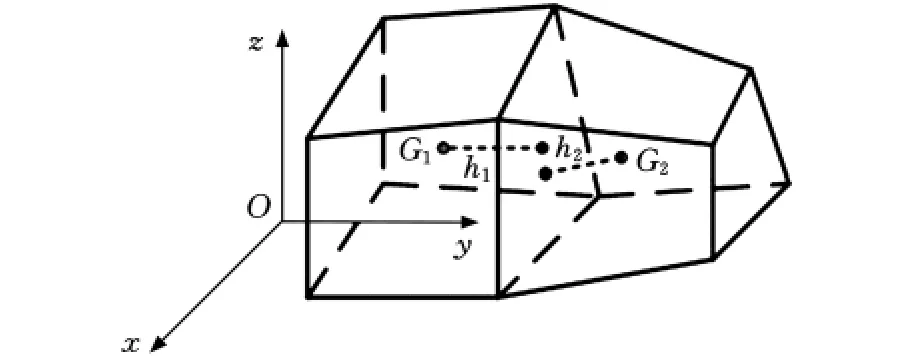
圖1 界面元模型

在圖1所示的界面元模型中，G1、G2分別為剛性單元e1、e2的形心，h1、h2分別為G1、G2至交界面的距離。界面元法將結構離散成有限多個塊體元和界面單元，并假設塊體單元的變形累積于界面。因此，塊體單元本身只有剛體位移，故用塊體單元形心的廣義位移（平動和轉動）作為基本未知量構造分片剛體位移模式來描述結構的位移場。由于界面上的任意一點均分屬相鄰的兩個塊體單元，因此可以求出界面上任意一點的相對位移，并由幾何關系得到界面上任一點的應變。界面元法的基本位移模式、應力公式及支配方程可參照文獻［7］表示如下：

式中，u為單元中任意一點的位移；ug為單元形心位移；N為形函數；（x，y，z）為界面上任意點的坐標；（xg，yg，zg）為單元形心點的坐標。

局部坐標系下單元界面上的應力σ1為

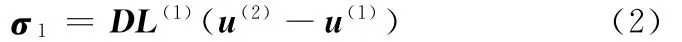
式中，D為界面彈性矩陣；L為界面局部坐標矢量的方向余弦矩陣，界面兩側的局部坐標方向相反，即L（1）＝ －L（2）；u（1）、u（2）為整體坐標系下界面兩側點的位移，上標（1）、（2）表示與界面相連的兩個單元。

界面元支配方程為

式中，K為整體剛度列陣；k為界面列陣；U為整體位移列陣，是由各塊體形心點廣義位移組成的待求未知量；為單元位移列陣ug和整體位移列陣U的轉換矩陣；R為整體載荷列陣；R（e）為作用在各個塊體元形心上的外力；Sj為界面。

2 結合部基本特性參數及表達式

機械結構中，結合面與結合部是兩個不同的概念。結合面是指兩個構件相接觸的表層部分，而結合部是指結合面和構成該結合面的構件在該結合面處的部分結構，因此結合部的特性除了與結合面特性相關之外，還與結合面附近的構件特性相關［4-5，10］。結合部的特性非常復雜，影響因素多，并多為非線性因素。為了便于分析，將影響結合部特性的因素分為三大類［5］：①與結構有關的因素，如結合部的類型、尺寸、形狀等；②與工況有關的因素，如接觸壓力、結合狀態(tài)、接觸面間介質狀態(tài)等；③與結合面固有特性有關的因素，如結合面的材質、熱處理狀態(tài)、加工方法和表面粗糙度等。

結合部諸多的影響因素使得要找到一種適用于所有結合部的、統(tǒng)一的、具有明確物理意義的特征參數的識別方法是不現實的。而根據模型的工況、建模和分析的具體要求，以及結合部的具體特性，綜合運用理論、數值和試驗方法建立實用的參數識別方法和數據庫是一種可行的選擇。將與結構有關的因素放在結合部特性分析中處理，將與工況及結合面固有特性有關的因素放在基礎特性參數中考慮，這樣就可以較方便地獲取具有通用特性的結合面基礎特性參數，供機械結構的結合部分析使用。

基于上述思想，通過試驗方法可得到結合面單位面積上的法向參數關系式［10］：

式中，c、m為與結合面的材質、加工方法、粗糙度、結合面固定、介質等相關的系數，這些條件一定時，c、m也一定；pn為結合面的單位面積法向壓力；λn為單位面積上的法向變形。

對式（4）求導得

根據剛度的定義，可求得單位面積上的法向剛度kn為

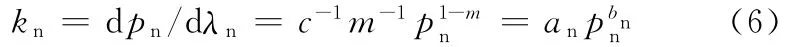
式中，an、bn為結合面法向特性參數，不同條件下的an、bn由試驗測定；kn為面剛度，即面壓/變形。

同理，可得到單位面積的切向剛度kτ的表達式：

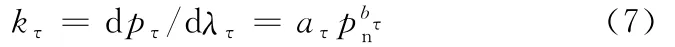
式中，pτ為結合面的單位面積的切向壓力；λτ為單位面積上的切向變形；aτ、bτ為結合面切向特性參數，它們與接觸面壓力、結合面材料、潤滑性質、加工方法、表面粗糙度等因素有關。

式（7）中的pτ和λτ的比例關系與pn有關［10］。例如，一組由磨削加工的45鋼組成的機械結構，當結合面間無油液介質時，其單位面積剛度可表示為

式（8）、式（9）中，pn的單位為 MPa，kn、kτ的單位為 MPa/μm。

結合面的接觸剛度不是一個定值，它隨接觸面面壓的變化而變化。在低面壓時，剛性比較弱，而高面壓時剛性則較高。在實際應用中，由于結構表面的加工質量及不同的載荷工況，結合面可能接觸，亦可能不接觸，表現出較強的非線性特征。

3 界面元法在機械結構結合部中的應用

3.1 機械結構結合部界面元模型

由于界面元采用分片剛體位移模式，因此在塊體單元的界面上可以允許位移不連續(xù)，這樣就能較好地反映結構的滑移、開裂等變形特征；通過在界面上設置塑性元件、黏性元件和接觸元件等，界面元法也能方便地求解各類非線性和時效響應問題；因為界面應力依賴于連接相鄰單元微分條的相對變形量，界面元法應力的計算精度一般不低于位移的精度，因此提高了應力狀態(tài)判據的可靠性，保證了非線性解不致出現漂移現象；另外，界面元模型中離散塊體單元可為任意形狀［7］，因此在不同介質的交界面上無需布置其他接觸單元，避免了復雜結構的網格剖分困難。

在對機械結構進行分析、建立結合部界面元模型時，確定結合部的特性參數十分重要。圖2是由構件Ⅰ和構件Ⅱ組成的僅有一個結合面的結合部示意圖。建立界面元模型時，將此結構分為A、B和結合部三部分，其中A的特性與構件Ⅰ相同，B的特性與構件Ⅱ相同，結合部是由構件Ⅰ和構件Ⅱ的部分共同組成，可將其看成一個整體，其特性參數可由如下方法得到。

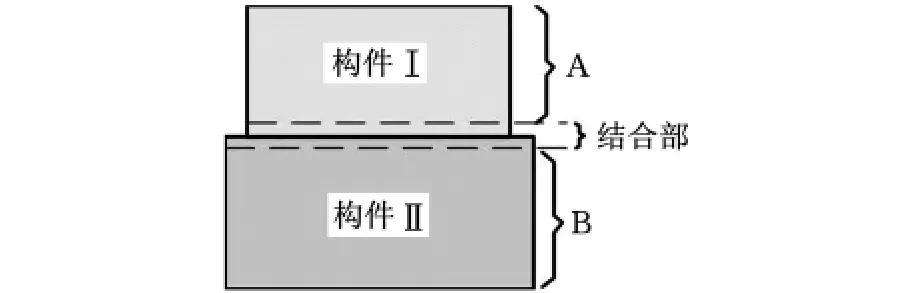
圖2 單平面結合部

根據式（5）、式（6），可得到在接觸面壓力、結合面材料、潤滑性質、加工方法、表面粗糙度等眾多影響因素作用下的單位面積上的法向剛度kn和切向剛度kτ。由赫茲理論，可得到微凸體相互接觸的法向接觸剛度kn［11-12］：

式中，a為微凸體間的接觸面積；E為結合部的彈性模量。

式（10）可改寫成

根據離散單元中的應力波傳播條件，可得到法向剛度和切向剛度的比例式［13］：

式中，μ為結合部泊松比。

式（12）可改寫成

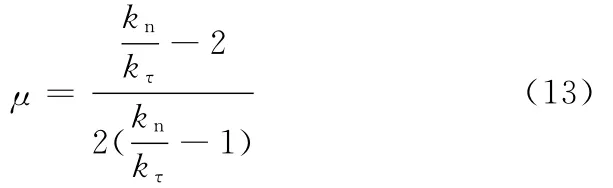
由于界面元支配方程與有限元支配方程在形式上十分相似，其實質都是離散點上的平衡條件，即有限元支配方程表示單元節(jié)點的平衡，而界面元方程則表示塊體單元形心點的平衡。因而界面元法和有限元法的解題思路、計算公式及運算步驟也十分相近，均是首先進行單元分析，再進行整體集合，求出基本未知量，最終求得所有形心點（節(jié)點）的位移列陣和單元應力。

3.2 螺栓連接的機械結構算例

螺栓連接的機械結構試驗模型如圖3所示［14］，模型由Ⅰ、Ⅱ、Ⅲ、Ⅳ四構件組成。構件Ⅰ、Ⅱ的材料均為45鋼，彈性模量E＝206GPa，泊松比μ＝0.26；Ⅰ、Ⅱ兩構件之間接觸表面磨削加工，粗糙度Ra為0.8μm，干接觸、無油；構件Ⅰ固定不動；構件Ⅲ為彈簧墊圈，型號為GB/T93 12；構件Ⅳ為六角頭全螺紋螺栓，型號為GB/T5781 M12×50；螺栓Ⅳ與構件Ⅱ間隙配合，試驗中通過轉動螺栓Ⅳ施加載荷。

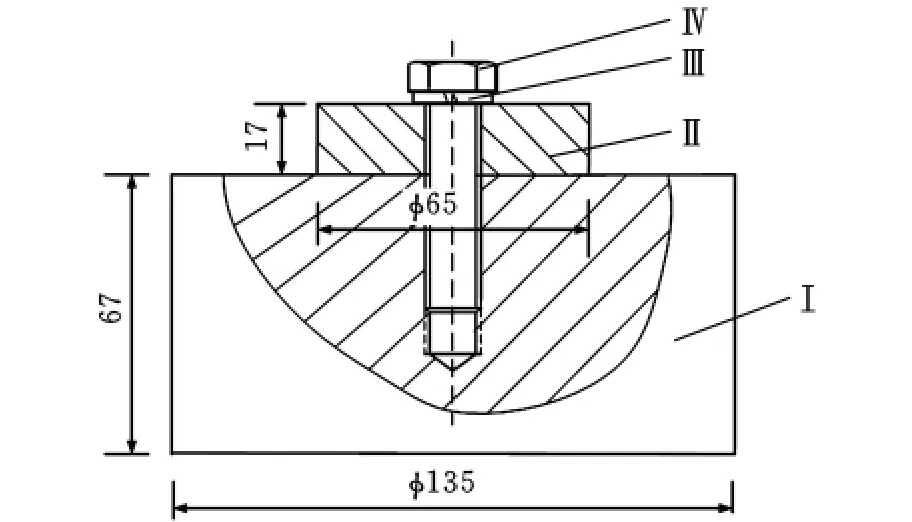
圖3 螺栓連接的機械結構試驗模型

圖4所示為螺栓連接的機械結構試驗簡化模型，將與構件Ⅰ連接的螺栓Ⅳ部分和構件Ⅰ簡化成為一個整體，構件Ⅱ的上表面A面承受環(huán)形均布載荷q，試驗中q的取值分別為14.7MPa、31.3MPa、46.6MPa。模型采用圓弧三角體單元和扇形體單元剖分，共有456個塊體元和1008個界面元。圖5為機械結構試驗模型各測試點分布圖，位于構件Ⅱ上表面A面，測試點有a、b、c、d、e、f共6個。

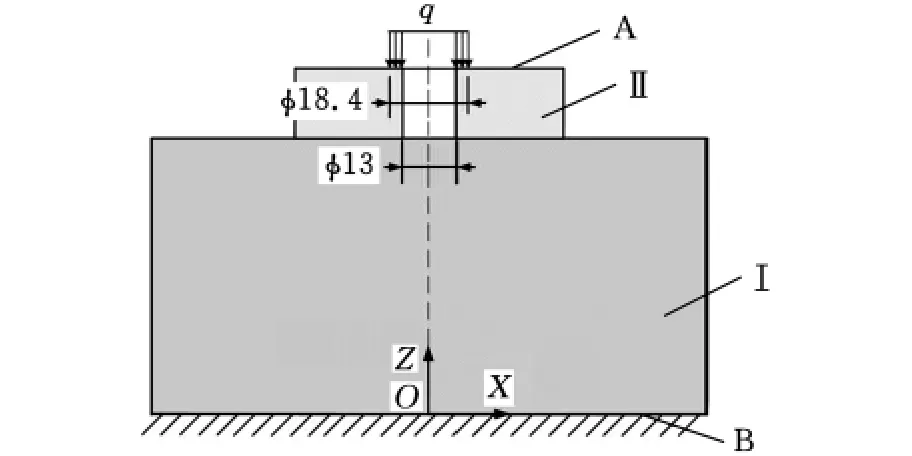
圖4 機械結構簡化模型

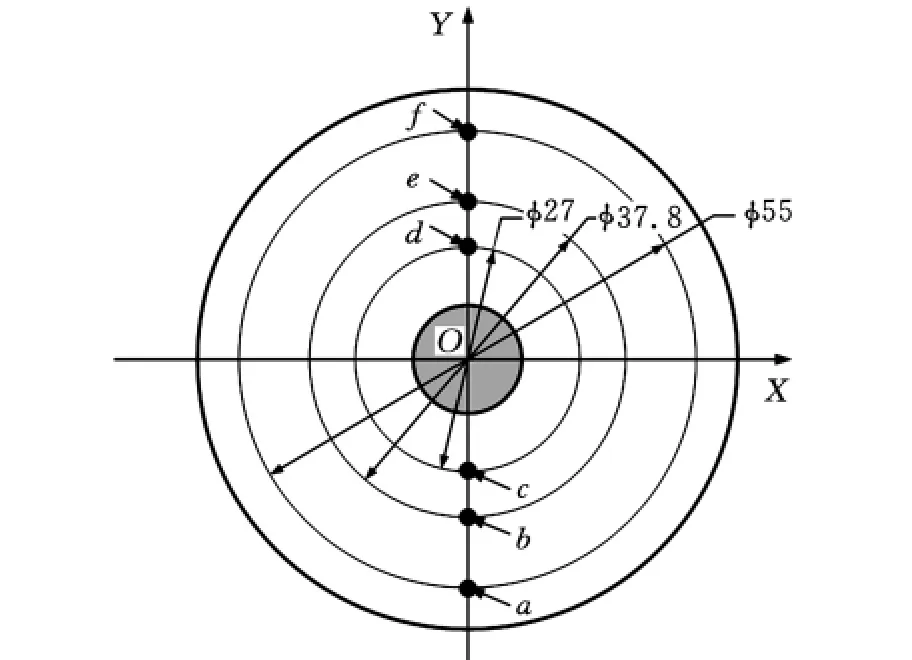
圖5 構件Ⅱ的A面測試點分布圖

圖6為不同載荷作用下構件Ⅱ的A面各測試點Z向變形計算值與實測值的對比圖。圖6a、圖6b、圖6c中構件Ⅱ的A面所受的均布載荷分別為14.7MPa、31.3MPa、46.6MPa。

從圖6的結果可以看到，在三種不同載荷作用下，面A各測試點Z向變形計算值與實測值均非常接近，并且隨著載荷的變化各測試點在Z向的變形趨勢與實際情況也是一致的。比較結果表明，建立機械結構結合部界面元模型時，基于赫茲理論和離散單元中的應力波傳播條件，由單位面積法向剛度kn和切向剛度kτ推導得到的結合部的等效特性參數E和μ是準確的；用界面元法解決機械結構的結合部問題是可行的。

4 結論

（1）由于界面單元采用了分片剛體位移模式，因此用界面元法對機械結構進行力學分析時，在零部件的結合部無需增加任何形式的接觸單元就可以有效地模擬結構的不連續(xù)性。

（2）建立機械結構結合部界面元模型時，結合部的等效特性參數E和μ可根據赫茲理論和離散單元的應力波傳播條件，由單位面積的法向剛度kn和切向剛度kτ推導得到。

圖6 構件Ⅱ的A面各測試點Z向變形計算值與實測值對比曲線

（3）螺栓連接裝置的計算和試驗結果表明，用界面元法可以有效地解決結構的結合部問題，該方法為整體研究和分析機械結構開辟了一條新思路，提供了一種新方法。

［1］趙宏林，昊智恒，賀艷荃，等.結合部特性參數及其在機床結構建模中的融合技術［J］.制造技術與機床，2007（5）：51－54.

［2］伊東誼.現代機床基礎技術［M］.北京：機械工業(yè)出版社，1987.

［3］黃玉美，董立新，董獻國，等.機械平面結合部靜特性的研究及其在機床CAD中的應用［J］.工程力學，1995，12（1）：66－71.

［4］趙宏林，丁慶新，曾鳴，等.機床結合部特性的理論解析及應用［J］.機械工程學報，2008，44（12）：208－214.

［5］王世軍，黃玉美.機床導軌結合部的有限元模型［J］.中國機械工程，2004，15（18）：1634－1636.

［6］Kim J，Yoon J C，Kang B S.Finite Element Analysis and Modeling of Structure with Bolted Joints［J］.Applied Mathematical Modelling，2007，31：895－911.

［7］卓家壽，章青.不連續(xù)介質力學問題的界面元法［M］.北京：科學出版社，2000.

［8］章青，周資斌，卓家壽.分區(qū)界面元－有限元－無限元混合模型［J］.計算力學學報，2005，22（1）：8－11.

［9］Kawai T，Toi Y.A New Element in Discrete Analysis of Plane Strain Problems［J］.Production Technology，1977，294（4）：204－207.

［10］黃玉美，張廣鵬，高峰.虛擬樣機整機結構特性邊界元仿真［M］.北京：機械工業(yè)出版社，2004.

［11］張學良，黃玉美，傅衛(wèi)平，等.粗糙表面法向接觸剛度的分形模型［J］.應用力學學報，2000，17（2）：31－35.

［12］Majumdar A，Bhushan B.Fractal Model of Elastic－plastic Contact Between Rough Surfaces［J］.Journal of Tribology，ASME，1991，113：1－11.

［13］邢紀波，俞良群，張瑞豐，等.離散單元法的計算參數和求解方法選擇［J］.計算力學學報，1999，16（1）：47－51.

［14］Marshall M B，Lewis R，Dwyer－Joyce R S.Characterisation of Contact Pressure Distribution in Bolted Joints［J］.Strain，2006，42（1）：31－43.