基于靜力平衡原理的三維均質(zhì)實體測量方法

甘 勇

桂林電子科技大學(xué)，桂林，541004

0 引言

隨著現(xiàn)代制造技術(shù)、快速原形制造技術(shù)和反求工程技術(shù)的快速發(fā)展，研究開發(fā)高精度、低成本的三維實體無損測量技術(shù)有著越來越重要的現(xiàn)實意義。目前的三維實體測量方法主要有有損測量和無損測量兩種，有損測量方法測量精度較高，但其測量速度慢、測量時間長，測量時要破壞被測零件，故測量成本較高，應(yīng)用受到限制。目前應(yīng)用較多的無損測量方法是光學(xué)測量方法，但該方法無法測量物體的內(nèi)部輪廓，存在光學(xué)測量的盲點(diǎn)，且測量所得的數(shù)據(jù)點(diǎn)云龐大，雜亂無序，有的甚至殘缺不全；另外，現(xiàn)有核磁共振成像和CT掃描方法能夠測量物體的內(nèi)部輪廓，但這兩種方法的成本很高，對可測零件的尺寸有限制，測量精度低，特別是對被測實體的材料有限制［1－2］。目前基于浮力的三維測量方法可無損測量不溶于液體的均質(zhì)實體，測量精度較高，能測量含有復(fù)雜內(nèi)部輪廓的實體，但對于內(nèi)部輪廓與外部不相通的均質(zhì)實體也無法測量，且測量精度和可靠性受到液體的動態(tài)特性和不穩(wěn)定性的影響［3－4］。國內(nèi)外學(xué)者雖然在三維實體的測量技術(shù)方面做了大量的研究工作，也取得了不少的理論研究成果，并基于其研究成果開發(fā)了不少的工業(yè)產(chǎn)品，但到目前為止，還沒有找到一種理想的三維實體的無損檢測方法。針對這一技術(shù)難題，本文提出了一種基于靜力平衡原理的三維實體無損檢測方法，本方法應(yīng)用分層原理，通過測量平衡系統(tǒng)中各力的變化值，根據(jù)空間力系平衡原理，推算出被測實體每層的質(zhì)量及層中各微小單元體的質(zhì)量和空間坐標(biāo)，能對具有復(fù)雜內(nèi)部輪廓的實體進(jìn)行三維測量。

1 測量方法總體方案設(shè)計

在物體三維空間單元表示法中，空間單元體將空間分割成均勻的立方形網(wǎng)格，可以根據(jù)實體所占據(jù)的網(wǎng)格位置來定義物體的形狀和大小。若此位置為物體所占據(jù)，即單元被填充，其質(zhì)量視為單元質(zhì)量1，稱為實單元體；反之，空單元體以0表示。基于空間單元表示法研究均質(zhì)實體，構(gòu)建計算模型，可視其由單元正方體構(gòu)成，采用基于二進(jìn)制像素的三維重構(gòu)方法，可取實單元體的質(zhì)量為1，空單元體的質(zhì)量為0，即所有像素值只能在（0，1）2個可能的離散值中選取，以此來表達(dá)空間圖像單元體的有無［5－6］。本文測量方法根據(jù)杠桿平衡系統(tǒng)中力的變化實現(xiàn)無損分層測量，以杠桿平衡系統(tǒng)中力與力矩平衡和其與實體重量的關(guān)系為基礎(chǔ)，通過按一定方向越過支點(diǎn)微小位移，測量杠桿平衡系統(tǒng)中實體每個不同位置的受力變化大小，求解被測實體各片層的質(zhì)量和相應(yīng)片層的重心坐標(biāo)值。建立各片層質(zhì)量和所含微小單元體的方程組及重心坐標(biāo)方程組，通過智能計算求解方程組，獲得各單元體的質(zhì)量和其空間坐標(biāo)值，進(jìn)而對獲得的點(diǎn)云數(shù)據(jù)進(jìn)行圖像重構(gòu)。根據(jù)測量需求設(shè)計的總體方案原理圖如圖1所示，其測量系統(tǒng)主要由杠桿平衡系統(tǒng)、精密測力系統(tǒng)、裝夾系統(tǒng)、精密運(yùn)動系統(tǒng)及計算機(jī)組成。

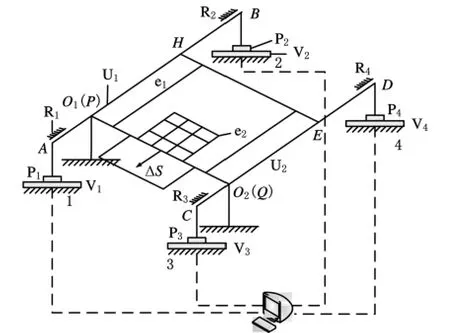
圖1 三維均質(zhì)實體無損測量方法原理圖

杠桿平衡系統(tǒng)包括均質(zhì)杠桿U1和U2、支撐平臺e1和4個自動配重系統(tǒng) P1、P2、P3、P4；杠桿U1的支點(diǎn)O1和杠桿U2的支點(diǎn)O2對稱平衡地設(shè)置在相應(yīng)的杠桿上；支撐平臺e1與上述杠桿U1和杠桿U2之間通過4個固定力接觸點(diǎn)P、Q、H和E相連接；其中，固定力接觸點(diǎn)P和固定力接觸點(diǎn)H位于杠桿U1上，且固定力接觸點(diǎn)P與杠桿U1的支點(diǎn)O1重疊；固定力接觸點(diǎn)Q和固定力接觸點(diǎn)E位于杠桿U2上，且固定力接觸點(diǎn)Q與杠桿U2的支點(diǎn)O2重疊；固定力接觸點(diǎn)P和固定力接觸點(diǎn)Q的連線與兩杠桿U1和U2均垂直；固定力接觸點(diǎn)H和固定力接觸點(diǎn)E的連線也與兩杠桿U1和U2均垂直；支撐平臺e1在系統(tǒng)中本身的重力及力矩已知不變，并可以通過杠桿系統(tǒng)平衡掉；杠桿U1和杠桿U2的4個端點(diǎn)A、B、C和D上分別固定懸掛有一自動配重系統(tǒng)P1、P2、P3和P4。杠桿平衡系統(tǒng)快速調(diào)節(jié)杠桿U1和U2的平衡穩(wěn)定，保護(hù)支點(diǎn)結(jié)構(gòu)，維持系統(tǒng)平衡。為了提高測量精度，實現(xiàn)杠桿系統(tǒng)的快速穩(wěn)定，以及保護(hù)精密測力儀器，杠桿U1和U2的4個端點(diǎn)A、B、C、D處各設(shè)有一限位器R1、R2、R3和R4。杠桿平衡系統(tǒng)的4個測力系統(tǒng)處各設(shè)有一個精密測力儀器V1、V2、V3和V4，該精密測力儀器的采集信號輸出端均連接至計算機(jī)中。4個精密測力儀器用于被測實體e2發(fā)生位移時，實時測量各點(diǎn)的變化力。由于4個精密測力儀器的測量精度高、量程小，因此，設(shè)計了4個自動配重系統(tǒng)P1、P2、P3和P4進(jìn)行配重，以解決其測量量程問題。裝夾系統(tǒng)包括包容立方體機(jī)構(gòu)，采用最小包容原則讓被測實體e2裝夾其中。精密運(yùn)動系統(tǒng)的控制端與計算機(jī)相連，精密運(yùn)動系統(tǒng)的動力輸出端則與裝夾系統(tǒng)相連，通過計算機(jī)指令控制包容有被測實體的裝夾系統(tǒng)實現(xiàn)精密位移。

2 測量方法數(shù)學(xué)模型建立及求解分析

均質(zhì)杠桿U1和U2分別對O1和O2點(diǎn)對稱平衡，為簡化計算，系統(tǒng)受力分析中均不計入。假設(shè)被測實體片層微小單元體為正方體且邊長為ΔS，被測實體在支撐平臺e1上，通過精密位移系統(tǒng)帶動實現(xiàn)每次的微小位移ΔS，從而實現(xiàn)每個測量方向上各個片層按序移過支點(diǎn)，達(dá)到測量計算的目的。以支點(diǎn)O1和O2的連線中點(diǎn)O為坐標(biāo)原點(diǎn)，將平行于杠桿的方向設(shè)為X軸方向，支點(diǎn)O1和O2的連線設(shè)為Y軸方向，垂直于X軸和Y軸的平面方向設(shè)為Z軸方向，建立空間三維坐標(biāo)系。以計算被測實體在X軸測量方向上進(jìn)行平移時所獲得的片層質(zhì)量和相應(yīng)重心坐標(biāo)為例，進(jìn)行測量裝置各部件受力分析，如圖2所示。已知質(zhì)量為M的被測實體所受的重力為G，將裝夾有被測實體的包容立方體放置于杠桿平衡系統(tǒng)的支撐平臺e1上，并讓包容立方體所測片層方向的起始邊緣與支點(diǎn)O1和O2的連線垂直相對，且將其狀態(tài)設(shè)為被測實體的初始狀態(tài)；通過調(diào)節(jié)自動配重系統(tǒng)，使杠桿平衡系統(tǒng)處于平衡穩(wěn)定狀態(tài)，同時，精密測力儀器測量并記錄下該時刻杠桿平衡系統(tǒng)的4個測力點(diǎn)所受的力FA（0）、FB（0）、FC（0）和FD（0），并將其返回至計算機(jī)中。在初始位置，當(dāng)杠桿U1平衡時（圖2a），分別對支點(diǎn)O1和支點(diǎn)B進(jìn)行受力分析，有

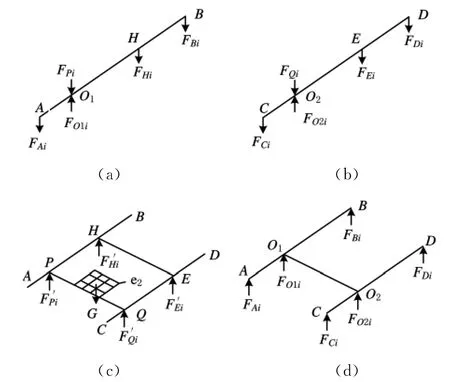
圖2 測量裝置各部件受力分析圖

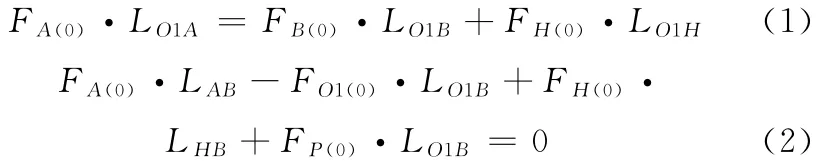
式 中，LO1A、LO1B、LO1H、LAB、LHB分別為 其下標(biāo)兩點(diǎn) 之間的距離。

在初始位置，當(dāng)杠桿U2平衡時（圖2b），對支點(diǎn)O2和支點(diǎn)D進(jìn)行受力分析，有

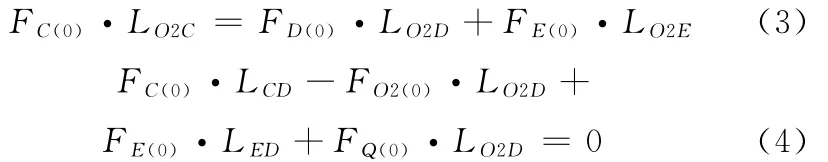
式中，LO2C、LO2D、LO2E、LCD、LED分別為 其下標(biāo)兩 點(diǎn) 之間的距離。

系統(tǒng)PQEH平衡時（圖2c），對軸PQ進(jìn)行受力分析，有

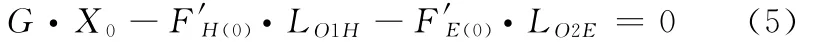
式中，X0為被測實體的重心坐標(biāo)值；F′H（0）、F′E（0）分別為FH（0）、FE（0）的反 作 用 力，且 其 各 值 已 知 并 可 測 出；LO1H為其下標(biāo)兩點(diǎn)之間的距離。

系統(tǒng)PQEH平衡時，對軸EH進(jìn)行受力分析，有

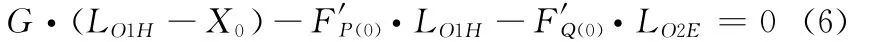
式中，F(xiàn)′P（0）、F′Q（0）分別為FP（0）、FQ（0）的反作用力，且其各值已知并可測出。

整個系統(tǒng)平衡時（圖2d），對軸O1O2進(jìn)行受力分析，有

式中，LO1B、LO1A分別為其下標(biāo)兩點(diǎn)之間的距離。

計算機(jī)依據(jù)式（1）～式（7）聯(lián)立求解出被測實體初始狀態(tài)下的重心坐標(biāo)值X0、支點(diǎn)O1和支點(diǎn)O2所受的力FO1（0）和FO2（0），以及固定力接觸點(diǎn)P、Q、H和E所受的力FP（0）、FQ（0）、FH（0）和FE（0）。

保持被裝夾系統(tǒng)的測量方向不變，讓精密運(yùn)動系統(tǒng)在計算機(jī)指令控制下帶動裝夾系統(tǒng)的包容立方體沿其X軸負(fù)方向每次平移ΔS后，通過調(diào)節(jié)自動配重系統(tǒng)使杠桿平衡系統(tǒng)處于平衡穩(wěn)定狀態(tài)，此時精密測力儀器測量出被測實體在第i（i＝1，2，…，n）層片層位置時杠桿平衡系統(tǒng)的4個測力點(diǎn)所受的力FA（i）、FB（i）、FC（i）和FD（i）。同上所述，杠桿U1平衡時，分別對支點(diǎn)O1和支點(diǎn)B進(jìn)行受力分析；杠桿U2平衡時，分別對支點(diǎn)O2和支點(diǎn)D進(jìn)行受力分析；系統(tǒng)PQEH平衡時，分別對軸PQ和對軸EH進(jìn)行受力分析；整個系統(tǒng)平衡時，由于只有被測實體移動，其系統(tǒng)力矩變化相當(dāng)于由片層質(zhì)量引起，對軸O1O2進(jìn)行受力分析，可列7個方程進(jìn)行求解。計算機(jī)依據(jù)列出的靜力平衡方程組聯(lián)立求解出被測實體平移i次后第i層的片層重力Wi，以及支點(diǎn)O1和支點(diǎn)O2所受的力FO1（i）和FO2（i），固定力接觸點(diǎn)P、Q、H和E所受的力FP（i）、FQ（i）、FH（i）和FE（i）。除去已測部分即未測部分的重心坐標(biāo)Xi的方程為

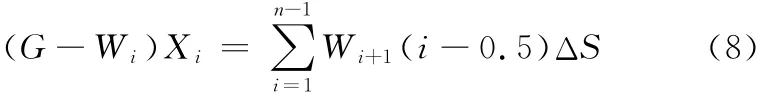
結(jié)合重力公式Wi＝miZg，即可獲得被測實體在X軸測量方向上每片層的質(zhì)量miZ，其中下標(biāo)Z表示總質(zhì)量。依次對被測實體的X軸方向、Y軸方向和Z軸方向，以及3個對角方向進(jìn)行測量，且沿X軸、Y軸和Z軸3個方向測量時，每次平移微小單元體邊長ΔS，從而獲得被測實體在X軸、Y軸和Z軸3個測量方向上的每片層的質(zhì)量和相應(yīng)的重心坐標(biāo)值。測量被測實體時，沿3個對角平面方向進(jìn)行測量，每次平移ΔS時，就能獲得被測實體在3個對角平面測量方向上的每片層的質(zhì)量miZ和相應(yīng)的重心坐標(biāo)值，上述測量一共獲得6個方向上的每片層的質(zhì)量和相應(yīng)的重心坐標(biāo)值。

將包容立方體即被測實體分為n3個正方體的微小單元體，每個實微小單元體的質(zhì)量為m，則第i層的總質(zhì)量為

式中，mij為第i層第j個微小單元體，i＝1，2，…，n。

當(dāng)被測實體e2移過第i層時，重心坐標(biāo)方程為

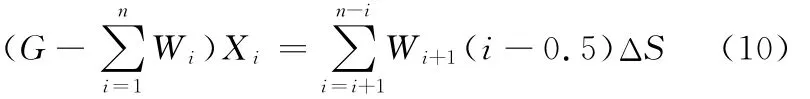
式中，Wi為第i層片層重力；Xi為未測部分的重心坐標(biāo)。

若已知微小單元體的質(zhì)量為m，則由微小單元體定義可知：所有微小單元體在實體空間只有兩種情況存在，要么為實單元體，即質(zhì)量為m；要么為空單元體，即不存在，質(zhì)量為0。其數(shù)學(xué)表達(dá)式為

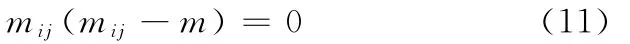
除可沿X、Y、Z3個方向進(jìn)行測量外，通過改變被測實體的測量方向，還可沿各個對角平面的方向進(jìn)行測量，即共有6個方向可供測量。故每一片層中的微小正方單元體的質(zhì)量和可列一個線性方程，以及一個重心坐標(biāo)計算線性方程。若一個實體共有N個微小正方單元體，當(dāng)其在X、Y、Z3個方向上的每個單元體按坐標(biāo)方向?qū)R時，一個坐標(biāo)方向共可列出2N1/3個線性方程，則在X、Y、Z3個方向上進(jìn)行測量時，共可列出6N1/3個線性方程；當(dāng)沿各個對角平面方向進(jìn)行測量時，共有6個方向，若每個方向只計片層質(zhì)量方程，每片層一個方程，則共有6N1/3個方程；因此，在不同方向測量時，最少可列出12N1/3個線性方程。另外，還存在m1（m1—m）＝0，m2（m2—m）＝0，…，mN（mN－m）＝0等N個非線性方程，經(jīng)過質(zhì)量歸一化處理以后，用這N＋12N1/3個方程優(yōu)化求解N個未知數(shù)，可高精度地求得每一單元的質(zhì)量，從而獲得實單元質(zhì)量的三維坐標(biāo)值。

3 實驗驗證

根據(jù)測量總體方案進(jìn)行初步實驗，實驗中的精密運(yùn)動系統(tǒng)采用美國BAYSIDE LM系列運(yùn)動平臺，運(yùn)動平臺的重復(fù)定位精度達(dá)±5μm，其作用是控制定位平臺，實現(xiàn)被測實體的精確位移。精密運(yùn)動平臺通過計算機(jī)控制指令控制被測實體按指定距離逐層位移。精密測力儀器采用瑞士梅特勒－托利多AB204－S型分析天平，其可讀性和重復(fù)性均為0.1mg，具有去皮功能。它通過串口與計算機(jī)直接相連，用于測量杠桿平衡系統(tǒng)中力的變化。模擬實驗測量采用圖3所示的標(biāo)準(zhǔn)件模型，初步實驗表明，本文實驗測量片層質(zhì)量的精度達(dá)到0.1mg，經(jīng)智能運(yùn)算測量的微小單元體的精度達(dá)到0.005%，測量重構(gòu)精度達(dá)到±0.2mm，其重構(gòu)點(diǎn)云圖如圖4所示。

圖3 被測標(biāo)準(zhǔn)件模型圖

圖4 轉(zhuǎn)換后的點(diǎn)云圖

4 結(jié)束語

本文測量方法所設(shè)計的測量平臺不僅研制成本低、經(jīng)濟(jì)性好，而且可實現(xiàn)自動測量，其測量方法能夠測量含有任意復(fù)雜內(nèi)外輪廓的實體，且測量速度快、測量數(shù)據(jù)少、分層有序、重構(gòu)簡單；測量數(shù)據(jù)所列數(shù)學(xué)方程均有可靠成熟的解法，編程計算幾乎不會給測量帶來新的誤差，其測量重構(gòu)精度可以控制在0.2mm以內(nèi)，基本滿足生產(chǎn)實際中三維實體測量的工程要求。

［1］郭迎福，李兵，李鵬南，等.反求工程中測量技術(shù)綜述［J］.礦山機(jī)械，2005，33（7）：75－77.

［2］金濤，陳建良，童水光.逆向工程技術(shù)研究進(jìn)展［J］.中國機(jī)械工程，2002，13（16）：1430－1436.

［3］Gan Yong，Zhong Jing Ru，Gan Du Fen.Research on 3DNon－ destructive Measurement System Based on Homogeneous Entity［J］.Advanced Materials Research，2011，201/203：63－68.

［4］Gan Yong.Design for 3dEqual－density Entity Contour Digital Measurement Device［C］//Proceedings of the Second International Symposium on Test Automation ＆Instrumentation.Beijing，2008：2306－2310.

［5］Gan Yong，Sun Ning，Kong Qinghua，et al.Research on Method of 3DContour Digital Measurement for Entity［C］//Proceedings of ICMEM2007 International Conference on Mechanical Engineering and Mechanics.Wuxi，China，2007：395－400.

［6］甘勇，孫寧，孔慶華.面向均質(zhì)實體的產(chǎn)品輪廓反求工程［J］.機(jī)械設(shè)計，2008（10）：8－11.