汽車座椅安全帶固定點強度試驗仿真模型改進

曹 奇 成艾國 周 澤 吳 飛

湖南大學汽車車身先進設計制造國家重點實驗室，長沙，410082

0 引言

《汽車座椅安全帶安裝固定點》是汽車被動安全中要求必須通過的重要法規。本法規試驗是一種破壞性試驗，即一臺白車身僅能進行一次試驗。重復的實車試驗必然造成大量的物資和時間浪費，因此在實際中多采用CAE仿真的方法來模擬這一試驗過程。目前國內類似的準靜態仿真主要基于隱式［1］和顯式［2－6］兩種有限元方法，但是隱式方法存在較大收斂性問題，需要花費大量時間進行前處理，而顯式分析模型計算精度通常低于隱式分析模型的計算精度。許多設計機構采用的仿真模型精度和穩定性有限，不能很準確、可靠地預測試驗結果，導致在節省成本和縮短時間上效果有限，從而缺乏說服力。本文通過考察常用的兩種仿真方法的優劣，選用較為合理的顯式有限元方法，并根據多次仿真和試驗對比，對傳統仿真模型中的關鍵參數進行逐步修正，最終得到與試驗高度吻合的結果。經多次重復試驗驗證表明，本文得出的結論能夠可靠地提高仿真精度，切實減少人力、物力和時間浪費。

1 顯式分析與隱式分析理論

對于一般的物理模型，總是可以建立下面的運動方程：

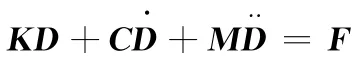
式中，K為剛度矩陣；C為阻尼矩陣；M為質量矩陣；D為節點位移；F為載荷。

任何一個物理過程，在仿真軟件中總是被抽象為上述運動方程。在求解這一物理模型的過程中，顯式分析和隱式分析都率先計算模型節點加速度，然后通過節點加速度積分依次求得節點速度和位移，兩者區別在于求解加速度的方法上。

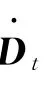
隱式分析采用迭代法，以常見的NewMark法為例。首先假設

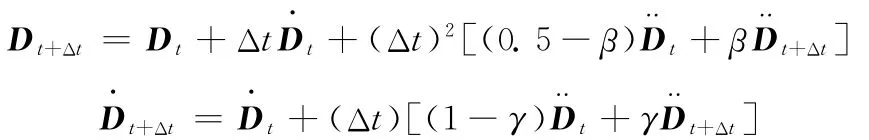
其中，β、γ是分析者根據系統特征人為設定的系數。上述假設在γ≥0.5且β≥（2γ＋1）2/16時是無條件穩定的。經過推導，得到

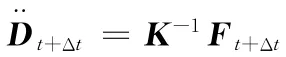
其中K矩陣求逆的過程很復雜，這就使得隱式分析耗費大量的計算資源。

隱式算法可以設置較大的時間步長，但是在面對復雜接觸和非線性問題時，大的時間步長會使解的收斂異常困難，因此不得不減小時間步長以獲得穩定合理的結果，甚至減小到與顯式算法時間步長等同的程度，此時將耗費巨大的計算資源，而顯式積分法能夠簡單有效地描述這些問題。因此，在模擬高速動力學事件、復雜接觸問題、非線性準靜態問題時，選用顯式積分方式更有優勢，這也是國內外主流技術機構越來越多采用顯式方法的原因。

2 安全帶拉伸試驗簡介

安全帶拉伸試驗用來驗證車載安全帶系統在車輛緊急減速時是否具備足夠的強度為乘員提供保護。通過圖1所示的上下人體模塊，沿車輛縱向中心平面與水平方向成向上（10±5）°的方向施加力載荷，以盡可能快的速度加載至規定值，并至少持續0.2s。通常整個實車試驗過程持續15s左右。對于三點式安全帶，上下人體模塊規定值均為（13500±200）N，對于兩點式安全帶，上車體模塊為（13500±200）N，下車體模塊為（22250±200）N。此外，如果有安全帶安裝點位于座椅上，還應加入相當于20倍座椅重力的力。

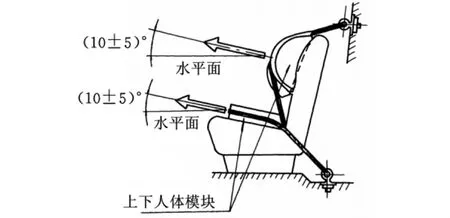
圖1 安全帶試驗加載示意圖

3 分析模型

利用有限元前處理軟件Hypermesh建立如圖2所示的安全帶試驗仿真模型。取D柱安全帶安裝點螺栓附件位置上一點，通過比較仿真與實際試驗中該點的位移，來判斷仿真模擬的精確程度。在仿真模型中，該節點號為2107497。

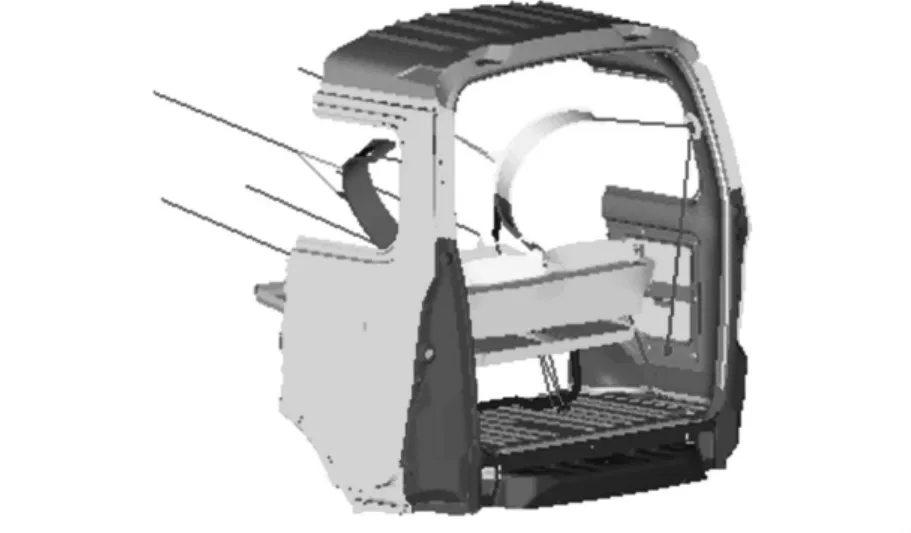
圖2 安全帶試驗仿真分析模型

圖3所示為初步建立的模型仿真結果與實車試驗結果，對比可見，兩者有較大差距。

圖3 實車試驗與初步仿真結果對比

實際試驗中，所選參考點位移為96.5mm，而在初步仿真模型中，這一參考節點位移達到127.256mm，后者比前者大31.6%。這一仿真結果低估了結構的強度，因而，在此仿真技術基礎上設計出的結構強度太過保守，從而提高了整車成本。下文將對單元類型、加載速度、加載方式、網格優化四個方面逐步進行分析調整，提高仿真精度。

3.1 單元類型選取

3.1.1 HL單元

HL單元基于薄殼單元的兩點基本假設：①垂直于中面的線應變可以忽略；②與中面平行的截面上法向應力可以忽略。

HL單元是從8節點體單元通過壓縮降級得到的，因此與體單元兼容性非常好。這樣，可以沿用LS－DYNA之前為體單元開發的各種技術。由于上述兩點假設只有在大位移和大應變條件下才認為是成立的，因此，HL單元適用于大位移和大應變問題的研究，但其缺點表現為需要耗費大量的計算時間。

3.1.2 BT單元

由Belytschko和Tsay共同開發的BT單元于1981年在LS－DYNA中得到應用，其主要優勢在于保證計算精度前提下有超高的計算效率。與HL單元相比，在采用厚度方向5點積分的情況下，BT單元僅需做725次數學操作，而HL單元需要做4050次數學操作，選擇性縮減積分HL單元更是需要做35 350次數學操作。

BT單元算法之所以高效，是因為采用了如下兩點簡化處理手段：①通過嵌入一個基于節點的固定坐標系分離了旋轉分量，避免了復雜的非線性力學特性；②在組集方程時，采用柯西應力矢量的形式，簡化了計算應力分量的難度。

在單元節點共面的情形下，這兩點簡化不會對計算精度造成任何影響，且能大幅減少計算耗時。傳統仿真模型中通常采用BT單元的形式進行計算。

3.1.3 BWC單元

由于BT單元局部坐標系是建立在平面幾何上的，故對于單元節點不共面的情況，即所謂的扭曲梁問題，BT單元無法給出合理的答案。BWC單元通過新增一個單元翹曲變形剛度，加入了單元扭曲的計算，從而對這一缺陷進行了修正。

3.1.4 全積分單元

BT單元和BWC單元都采用了縮減積分的方式，在單元面內只使用一個積分點，減少了積分次數，從而進一步提高了計算效率，同時引入了沙漏模式來控制縮減積分帶來的零能模式。全積分單元采用與BT單元相同的單元坐標系，但是在線性四邊形單元平面內選擇2×2個積分點，能夠處理單元的彎曲問題。如今在計算機硬件條件已經大幅改進的情況下，使用全積分單元的計算時間已經變得可以接受，而且其計算結果更加真實、精確。

3.1.5 結果對比

表1列出了選取四種單元得到的節點位移和計算時間。可以看出，BT單元和BWC單元分析結果區別不大，而全積分單元雖然計算時間稍長，但與BT單元相比，節點位移減小了8%。HL單元計算時間和計算精度都處于居中的水平。因此采用全積分單元使仿真結果更準確。在后續分析中，將采用全積分單元取代BT縮減積分單元。

表1 選取四種單元得到的節點位移和計算時間

3.2 加載速度選取

對于準靜態模擬而言，加載時間的確定是一個關鍵問題。對于一般的物理過程，如果按照其固有持續時間來加載，可以確定將獲得一個準確的解。而在實際仿真中，為了縮短計算時間，需要人為地提高載荷速率，只要能夠控制模型的動態效應，使結果受到慣性效應的影響很小，就可以認為等同于準靜態情況。由文獻［3］可知，加載速率在40km/h以下時顯示計算結果與準靜態結果非常接近。而本試驗并不以速度為輸入條件，因此加載速度難以控制。事實上，結構的最低模態，決定了其動態效應被激發的臨界點［7］。本文首先計算仿真模型的局部模態，然后以其最低模態為參考，確定合適的加載速度。

對安全帶固定點局部模型進行模態計算，得到一階模態仿真結果如圖4所示。

圖4 安全帶試驗仿真模型模態分析結果

根據仿真結果，該安全帶固定點局部結構的最低模態為76.1Hz，對應周期為12.5ms。當載荷周期為12.5ms時，頂蓋位置將發生共振，產生嚴重的動態效應。為了避免這種情況發生，應使載荷周期大于12.5ms。為此，加載時間分別取50ms、75ms、100ms、125ms，并分別保持20ms。

表2列出了在不同加載時間的情況下計算得到的節點位移及計算時間，其中，ts為實車試驗的加載時間，模型單元采用全積分單元。

表2 不同加載時間下的節點位移和計算時間

結果表明，加載時間從50ms增加至75ms時，模型計算結果有較大改進，節點位移的改進量約為17%，在加載時間為75ms時，節點位移的計算結果最接近實車試驗結果。繼續延長加載時間，仿真節點位移比實車試驗值逐漸偏小。因此，加載時間為75ms，即等同于模型最低模態對應周期的6倍時，仿真結果與試驗值最為接近。

3.3 加載方式選取

突變的加載會在模型中產生非真實的應力波，從而激發模型的振動，在準靜態分析的加載方式中，應盡量使加載力平滑。在LS－DYNA的關鍵字中，有兩種加載曲線定義方式，分別為斜坡加載和平滑加載，如圖5所示，其中上人體模塊施加力為13 700N，下人體模塊施加力為22 700N。

平滑曲線在整個加載過程中呈S形，其加速度曲線的二階導數連續，避免了加載初期和末期的加速度突變，也就避免了突然加載和突然卸載造成的沖擊振蕩。定義＊DEFINE＿CURVE＿SMOOTH中各參數值，就可以非常容易的得到平滑加載曲線。

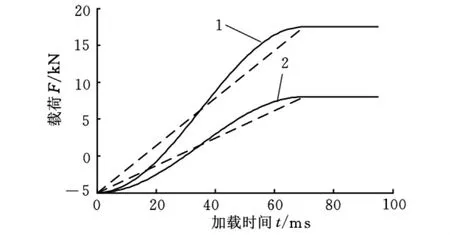
圖5 斜坡加載和平滑加載曲線

由斜坡加載和平滑加載得到的節點位移分別為96.7mm和98.4mm。結果表明，兩種加載方式對最終參考節點位移的影響不大，但是平滑加載能更快更平穩地達到穩定狀態。

3.4 網格局部優化

在某些較窄的焊接翻邊區域，往往有較大變形。傳統仿真模型沒有對這類區域進行特殊處理，翻邊只有1～2層網格，意味著此時寬度方向僅有2～3個節點，這將無法準確描述復雜的曲面變形。而且較少的節點也導致接觸搜索失效，該區域則會出現失真的穿透和毛刺現象。本文對這些區域網格進行了局部細化，其結果如圖6所示。圖6是細化前后的仿真結果對比。圖6a中，網格變形尖銳，不同部件之間甚至出現了交叉現象，這是非真實的。圖6b是經過細化網格后的仿真結果，局部變形更加光順，也沒有出現部件交叉的現象，細化網格后的仿真結果更加真實。

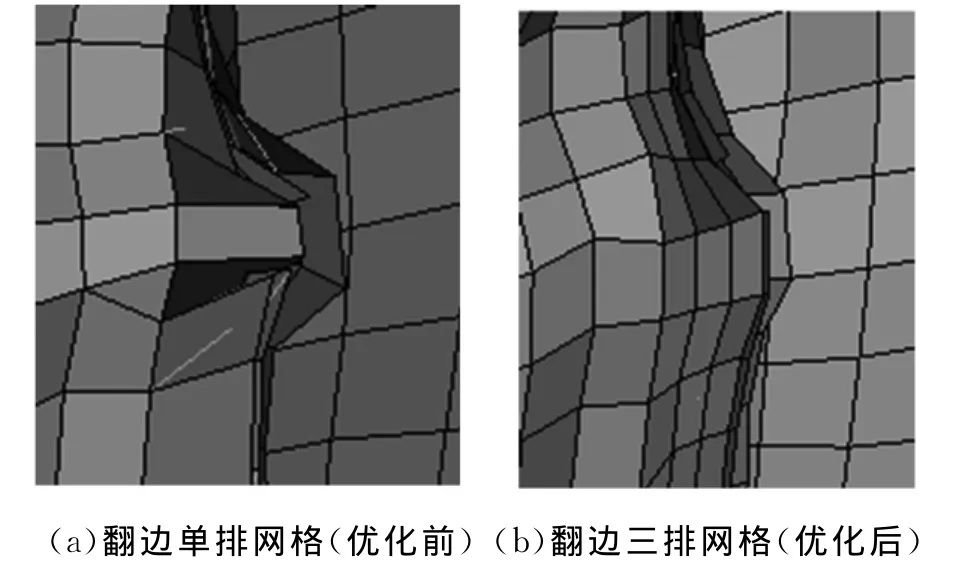
圖6 網格局部優化結果對比

3.5 最終結果及驗證

將優化的模型與最初模型對比，其結果如表3所示。

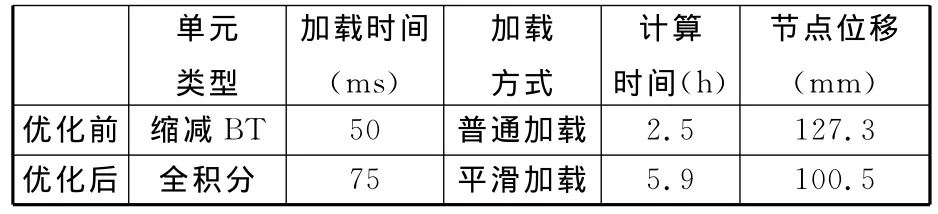
表3 模型優化前后的結果對比

由表3可見，對比模型優化前后的計算結果可見，優化后的局部變形光滑而真實。模型優化前后的仿真結果節點位移改進幅度達21%，實車試驗中該節點位移為96.5mm，模型優化后的節點位移誤差僅為4.1%。滿足工程應用需求。

從圖7的仿真與試驗對比中也容易看到，優化后結果變形與實車試驗變形結果接近度相當高。

圖7 實車試驗與優化后仿真結果圖

這種經過優化的模型已在多款國產微客的座椅安全帶仿真中得到使用，表4列出了其中三款車型共7次試驗的數據。可以看出，仿真誤差基本控制在試驗值的5%以內，其精度較高，穩定性較強。

表4 7次試驗與仿真結果節點位移表 mm

4 結束語

對于汽車座椅安全帶固定點試驗的仿真分析，使用基于顯式算法的計算模型，能夠較方便地模擬真實試驗過程。在此基礎上，通過改進模型關鍵參數和局部細節處理方法，使得仿真結果精確度和穩定性大幅提升，計算結果可以準確反映實際試驗結果，可靠的用于設計指導和性能評判依據，從而取代成本高、周期長的實車試驗過程，成為工程師結構設計的有力工具。

［1］徐中明，郝煒雅.汽車座椅強度及碰撞仿真分析［J］，重慶大學學報，2009，32（5）：512－515.

［2］胡玉梅.汽車正面碰撞設計分析技術及應用研究［D］.重慶大學，2002.

［3］苗強，葛如海，高衛民.車用兒童約束裝置建模與仿真分析［J］.上海汽車，2007（4）：20－24.

［4］朱靜.大客車頂部結構強度分析及翻滾碰撞性能研究［D］.西安：長安大學，2008.

［5］王青春，范子杰.利用LS－DYNA計算結構準靜態壓潰的改進算法［J］.力學與實踐，2003，25（3）：20－23.

［6］許早龍，范朝兵.基于LS－DYNA的汽車安全帶固定點強度研究［J］.力學與實踐，2010，32（3）：105－110.

［7］莊茁，ABAQUS/Standard有限元軟件入門［M］.北京：清華大學出版社，1998.