貝葉斯假設檢驗與經典假設檢驗的對比研究
張 靜
0 引言
顯著性檢驗在經典統計中作為統計推斷重要內容之一,被廣泛應用在各個領域。顯著性檢驗是通過樣本信息對總體的某個假設做出拒絕或不拒絕的決策,是用推斷的方法解決決策的問題,不能給出決策錯誤時所產生的損失大小,并且在使用顯著檢驗過程中出現一系列問題。相比之下貝葉斯檢驗方法能較好的處理這些檢驗問題。
1 經典檢驗結果的不確定性
經典假設檢驗首先根據問題的要求提出假設,通過給定的顯著水平確定檢驗的拒絕域,然后根據樣本是否落入拒絕域來判斷拒絕還是接受原假設。但是,在實踐中由于假設的建立不同、顯著水平α大小不同,往往會出現同一問題和同一組樣本數據得到完全相反的檢驗結果,使得檢驗所得的“顯著”結果在實際中并無重大意義。
假如有一組調研人員做了一個關于總體均值在0.12處的單側Z檢驗,顯著水平α=0.05,獲得抽樣結果z=0.015,若假設為 H0:μ≤0.12, H1:μ>0.12,由于拒絕域為{z ≥1.645},而z=0.015<1.645,z值沒有落入拒絕域故認為總體均值不大于0.12。然而若假設變為H0:μ≥0.12, H1:μ<0.12時,其拒絕域為{z ≤-1.645} ,而z=0.015>-1.645,z值沒有落入拒絕域,即認為總體均值不小于0.12,與上述的結論是相反的。
一個雙尾檢驗變為單尾時,檢驗結果有可能超越“統計顯著”的界限。假如我們做了一個雙尾Z檢驗,獲得抽樣結果z=1.85,檢驗p值≈0.06,當α=0.05時檢驗結果是不拒絕原假設,即不顯著。將檢驗改為單尾時,單尾檢驗p值比雙尾檢驗p值縮小一半,檢驗結果立即變為顯著的了。若將顯著水平α增大到0.07時雙尾Z檢驗又變為顯著了。
相比之下,貝葉斯檢驗中,無論如何建立假設,也無需給出顯著水平,只要給出參數的后驗分布,通過計算各假設的后驗概率,對假設的后驗概率大小的比較,就可以得到確切的檢驗結果,即檢驗結果是穩定的。
2 經典檢驗中顯著水平的誤導
在經典假設檢驗中,p值越小,意味拒絕H0的證據越充分。但事實上經典檢驗中p值常常是高估拒絕H0的證據。當樣本容量很大時,抽樣結果與H0的微小差別,總能得到一個極小的p值,導致拒絕H0的結論,然而這個結論并沒有實際意義。即便是在中等樣本量時,一個小的p值也幾乎不提供拒絕H0的證據,即經典的犯錯誤的概率或顯著性水平,把原假設是否有效引導到完全錯誤的印象中去。
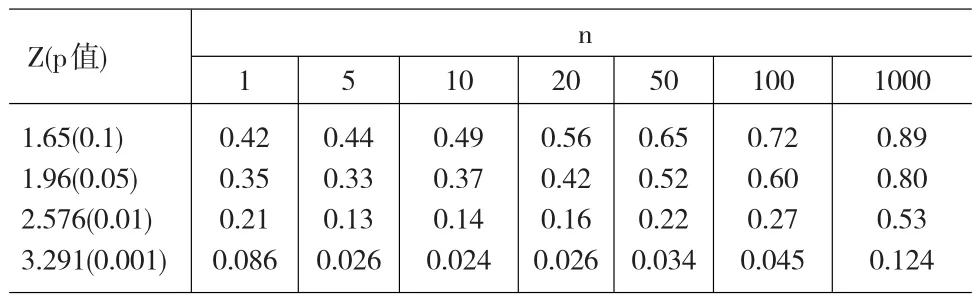
例如,假設觀測樣本 X1,X2,…,Xn來自分布N(θ,σ2),σ2已知。檢驗假設 H0:θ=θ0,H1:θ≠θ0,采用貝葉斯方法進行檢驗。給θ先驗分布為:在θ=θ0時π0=π(θ0)=1/2,在 θ≠θ0時 π(θ)=π1g1(θ),其中 π1=1-π0=1/2,g1為 N(μ,τ2),當給出先驗的具體值 μ=θ0,τ=σ時,可給出不同樣本容量n及不同抽樣結果下的p值及α0如下表。
Z(p值)n 1 5 1.65(0.1)1.96(0.05)2.576(0.01)3.291(0.001)0.42 0.35 0.21 0.086 0.44 0.33 0.13 0.026 10 0.49 0.37 0.14 0.024 20 0.56 0.42 0.16 0.026 50 0.65 0.52 0.22 0.034 100 0.72 0.60 0.27 0.045 1000 0.89 0.80 0.53 0.124
從表中的數據可以看出若由觀測值得z=1.96,意味經典檢驗中拒絕H0的顯著水平是0.05,由于0.05夠小,拒絕H0的證據看似足夠充分,所以結論是拒絕原假設。然而,H0的后驗概率是很大的,從小的n時的1/3,到大的n時接近1。即當p值為0.05時幾乎不提供拒絕H0的證據。同時可以證明,對任何合理的先驗,在同一組樣本數據下,經典檢驗中的較小的p值都對應較大的后驗概率α0。于是,出現了經典犯錯誤的概率或p值對否定H0的根據進行完全錯誤的描述[1]。
3 經典最優與貝葉斯方法的等價性
假設觀測樣本 X1,X2,…,Xn來自分布 N(θ,σ2),σ2已知,π(θ)~ N(μ,τ2),考慮檢驗 H0:θ≥θ0, H1:θ<θ0,若以“0—Ki”為損失函數,則可得貝葉斯檢驗的拒絕域為:,其中與經典的α水平、一致最大功效檢驗的拒絕域具有相同的形式。在經典檢驗中拒絕域的臨界值由α決定,而在貝葉斯檢驗中則由損失和先驗信息決定。結論是:(1)經典檢驗中α選取沒有準則,通常為0.05或0.01,但這個慣例并沒有嚴格地被大多數統計學家嚴格遵守,α的選擇具有主觀性;(2)經典犯第一類錯誤概率α不能說明犯錯誤時所產生的損失的大小;(3)每一α水平的最大功效檢驗相對應一個貝葉斯檢驗,即或者對假設的先驗及損失做主觀選擇或者對α水平做主觀選擇;(4)貝葉斯方法充分運用了合理的先驗信息及抽樣信息,并且給出決策錯誤時的損失,其結論更加可靠,因而貝葉斯方法可以看作是提供了一個選擇檢驗的顯著水平大小的合理方法。
4 經典檢驗不宜處理多個假設的情況
對于問題 H0:θ∈Θ0?H1:θ∈Θ1若 Θ0?Θ1≠Ω(Ω為參數空間),假設檢驗中常常存在兩者皆可的區域,即產生第三個假設θ∈Θ2。例如,若要求檢驗兩種藥物的治愈率 ,合 理 的 方 法 是 三 個 假 設 :H0:θ1-θ2<-ε,H1:θ1-θ2>ε H2:| θ1-θ2|≤ε,其中 ε>0 的選擇是認為|θ1-θ2|≤ε為兩種藥是等效的。經典假設檢驗中常處理的情況是非此即彼,對這類問題無法定義p值;另外,當檢驗涉及三個及三個以上的多重比較問題,經典的檢驗將增加犯第一類錯誤的概率,所以,經典假設檢驗方法亦不宜處理多重假設問題,而貝葉斯假設檢驗通過計算每一個假設的后驗概率,接受后驗概率最大的假設。因此,貝葉斯方法更易處理多個假設的檢驗問題。
5 結論
無論是經典假設檢驗,還是貝葉斯假設檢驗,人們關心的問題是假設檢驗的結果是否真能反應原假設的真偽,但以“顯著水平”為中心的經典假設檢驗理論并不能直接回答這個問題。本文通過對兩種檢驗方法的對比研究,指出了經典檢驗方法存在的一些問題,以及貝葉斯檢驗方法在解決這些問題時的優勢。
[1] [美]James O.Berger.統計決策論及貝葉斯分析[M].北京:中國統計出版社,1998.
[2] 傅軍和.經典檢驗p值的若干問題[J].統計與決策,2009,(1).
[3] 茆詩松.貝葉斯統計[M].北京:中國統計出版社,1999.
[4] 韋博成.參數統計教程[M].北京:高等教育出版社,2006.

