高爐生產過程的智能預測建模

劉慧，李沛然，包哲靜，王超，顏文俊

(浙江大學 電氣工程學院，浙江 杭州，310027)

隨著國民經濟的發展，鋼鐵在社會經濟中的重要性越來越突顯出來。其中高爐煉鐵占煉鐵行業的95%，使得高爐成了冶煉鋼鐵中的重要環節，而高爐爐溫的適合與穩定又是高爐鐵水質量的保證，是高爐長壽、高產、低耗的保證[1]。高爐煉鐵是指高爐生產時從爐頂裝入鐵礦石、焦炭、造渣用熔劑(石灰石)，從位于爐子下部沿爐周的風口吹入經預熱的空氣。在高溫下，一部分焦炭(有的高爐也噴吹煤粉、重油、天然氣等輔助燃料)中的碳同鼓入空氣中的氧燃燒生成的一氧化碳，在爐內一氧化碳上升過程中除去鐵礦石中的氧，從而還原得到鐵和二氧化碳，這稱為間接還原反應，一般發生在高爐中溫度低于1 100 ℃的時候；另一部分焦炭直接與鐵的氧化物發生反應還原出生鐵，稱為直接還原反應，一般在高爐中接近中心溫度最高的地方都發生直接還原反應；還有一部分鐵的氧化物被氫氣還原，生成的水一部分被碳和一氧化碳還原為氫氣，還有一部分在高爐上部被鐵礦石和焦炭吸收，以降低高爐爐口的溫度，保護高爐。煉出的鐵水從出鐵口放出。鐵礦石中未被還原的雜質和石灰石等熔劑結合生成爐渣，從渣口排出。產生的煤氣從爐頂導出，經除塵后，作為熱風爐、加熱爐、焦爐、鍋爐等的燃料[2]。在實際生產過程中，由于高爐結構的復雜性使得直接測量高爐內部溫度場分布變得困難，而爐溫與鐵水含硅量密切相關，故可以用鐵水硅含量代表高爐爐溫，將鐵水硅含量控制在一定的范圍內就成為了高爐研究的主要內容。目前國內外研究的比較多的是建立高爐的專家系統，包括日本川崎水島的“ADVANCED GO-STOP系統”、芬蘭羅德洛基公司的專家系統以及劉金琨等的高爐異常爐況神經網絡專家系統等[3]。但是這類專家系統也存在一些問題：首先，由于準確率主要取決于知識庫的知識多少及正確率，因此，專家系統成功與否要看工長的經驗成熟程度；其次，知識庫的內容、規則一般具有本高爐的特點，由于高爐個體的差異，知識庫的內容、規則需要很大的改變，系統移植能力差。為了克服這些缺點，本文作者提出智能復合模型，對歷史數據進行預處理后，運用 SVM建立不同工況下的鐵水硅含量預測模型；然后，應用模糊擬合推理找出各模型權重與生產輸入和模型輸出之間的關系，從而得到不同時刻各個模型的權重，進行多模型的智能融合，進而得到復合預測模型并不斷在線調整，以便控制和優化高爐生產過程。

1 高爐生產過程數據預處理

1.1 生產過程建模框架

整個建模過程可由以下幾個部分組成：工況分析模塊、數據處理模塊、單工況模型確立模塊、模型復合模塊。

工況分析模塊在獲得足夠多的歷史數據后對這些數據進行分析，提取出能夠反映高爐大多數工作情況的點，即不同的工況；

數據處理模塊根據各個工況的不同特點對其數據進行濾波去噪、剔除異點等預處理；

單工況模型確立模塊利用 SVM 分別對各工況的歷史數據進行建模，得到各個工況符合精度要求的模型；

模型復合模塊運用模糊邏輯推理得到各模型的權重系數，進行多模型的智能聯合。

參數調整模塊根據實際輸出與復合模型輸出之間的誤差修正各模型權重。

本文提出的高爐生產過程的模型是根據冶金高爐系統的現場數據以及系統工藝機理，基于 SVM 建立的不同工況下的多變量模型。整個建模流程如圖 1所示。

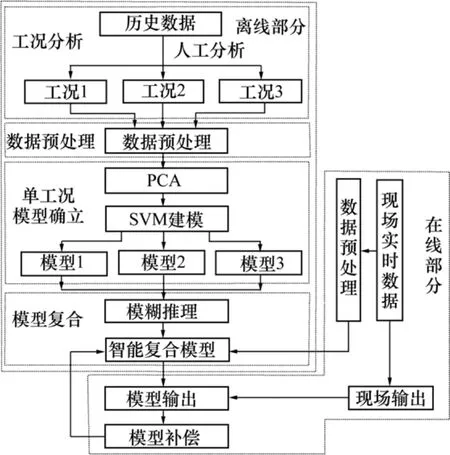
圖1 智能復合模型流程圖Fig.1 Flow of intelligent mixed predictive model

1.2 工況分析

為了獲得更加精確的高爐生產模型，本文基于對大量的高爐生產過程歷史數據的分析，根據專家經驗和鐵水Si含量的歷史數據，發現該高爐一般穩定在3個工作點，即高溫、適溫和低溫，各工作點的Si含量如圖2所示。

1.3 數據預處理

高爐鐵水硅含量受到眾多因素的影響，根據專家經驗爐溫較低時一般選擇較為密切的7個變量包括風量、風溫、風壓、噴煤量、下料量、透氣性、爐頂壓力。

由于高爐數據的采樣時間間隔不一樣，比如風量和風壓等變量每隔1 s采樣1次，而鐵水硅含量則是在每爐出鐵時采樣1次，所以需要先將所有采樣得到的數據化為同一采樣時間間隔。

另外由于采樣過程中可能會出現外界干擾、樣本不均勻等現象造成采樣得到的數據包含噪聲，所以采用滑動濾波對所得數據進行預處理，最后得到數據曲線的包絡線，取數據曲線上下包絡線的平均得到最終數據。圖3所示為以噴煤量、風量和透氣性這3個參數為例，描述了經過濾波后的歷史數據曲線。

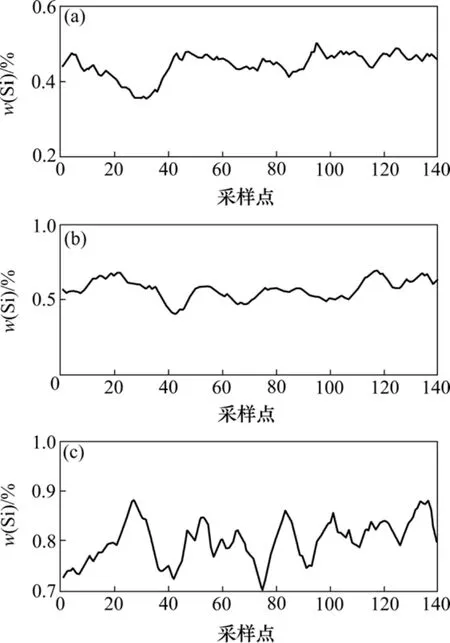
圖2 各工況下的Si含量Fig.2 Content of Si in every work condition

圖3 經過濾波后的曲線Fig.3 Filtered parameter data

2 單工況模型的建立

2.1 主元分析

主元分析是多元統計中的一種數據挖掘方法，利用降維的思想，在不丟失主要信息的前提下選擇較少的幾個綜合變量代替原來較多的變量，以排除原信息中相互重疊的部分[4-5]。而支持向量機(SVM)是Vapnik等[6-8]建立的理論體系，采用結構風險最小化原理，兼顧訓練誤差和泛化能力，在解決小樣本、非線性、高維數、局部極小值等問題中占優勢。以爐溫較低這一工況為例，單工況模型建立過程描述如下。

假設x=(x1, x2, …, xn)T，n=7代表這7個變量的經過處理后的歷史數據，計算相關系數矩陣R=(rij)7×7，進而求得該矩陣特征值λ1, λ2, …, λ7，如圖4所示，橫坐標表示構成矩陣的變量，縱坐標為矩陣中每個變量對應的特征值從大到小排列。

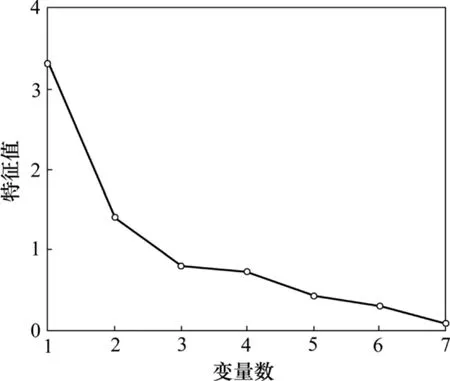
圖4 各個變量對應的特征值Fig.4 Eigenvalues of components

一般來說，選擇變量個數有2種方法：一種是選擇貢獻率大于1的所有變量，一種是選擇貢獻率累積大于 85%的所有變量。在此根據模型精度選擇變量個數。

表1 成分方差百分比Table 1 Component of variance %

首先選擇貢獻率最大的變量得到因子得分系數從而得到相應主成分表達式，將其作為輸入，運用支持向量機建立與鐵水硅含量之間的數學模型，并計算模型精度，若滿足要求，則到此為止；若大于要求的精度，則繼續選擇貢獻率稍小的變量。

2.2 支持向量機建模

由 Hilbert-Schmidt原理和文獻[10]可知：在求解上面風險函數的過程中，只涉及到樣本間的內積運算(xi, xj)，只要找到1個函數K(xi, xj)滿足Mercer條件，它就能對應某一變換空間中的內積，就可以用該函數代替此內積。

根據經驗，常用的有4種函數：線性核函數、多項式核函數、高斯徑向基核函數和樣條核函數。本文中選取三次多項式核函數d=3。由于訓練誤差大，故繼續選取貢獻率較大的變量，重復以上步驟，直到精度達到要求，最后的擬合效果如圖5所示。其他工況也用同樣的方法建立模型。

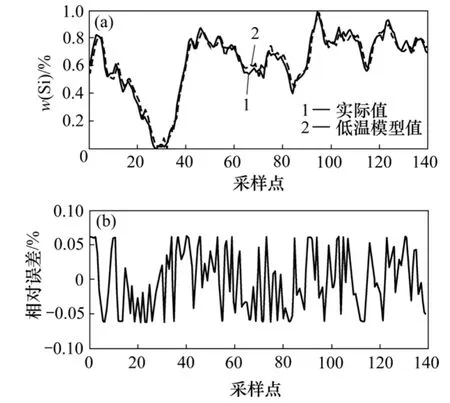
圖5 低爐溫預測效果Fig.5 Regression result at low temperature

圖5所示為低爐溫預測效果。圖5(a)中，實線表所示為預測結果與實際硅含量相比的誤差。從圖 5(b)示實際的硅含量，而虛線表示硅含量預測結果；圖5(b)可以看出：預測誤差能夠保持在8%以內，可以用該模型作為整個模型中的單模型來控制和優化生產過程。

然而，在實際的生產過程中，高爐精確工作在某一工況的情況是一種特例，大部分情況下高爐都不能完全工作在這些確定的工況，而是處于某些工況的過渡階段。這時候只有當工況劃分的足夠細致，才能反映高爐的每個工況，但是，這又會使建模變得相當復雜，大大增加了計算量，而且很多時候高爐工作情況本身的復雜性也使得高爐的劃分工況的工作變得很困難。基于這種情況，本文采用智能模糊模型聯合，它既可以反映高爐的特殊工況，又可以反映介于這些特殊工況之間的工作情況，并且工作量并沒有增加很多，在工程上是可實現的。

3 模型智能復合

得到各個工況下的預測模型后，進行基于規則的多模型的智能融合和在線調整，并將各個模型與其權重乘積之和作為實際的預測輸出，一方面軟化模型切換過程中系統參數變換帶來的影響，另一方面避免因爐況判斷不正確帶來的一系列影響。此方法對模型結構的變化無特別限制，只要模型的變化在模型集描述的范圍內即可[11]。其基本思想是：將當前系統輸入進入各個模型后得到各模型的預測輸出，根據這些預測輸出與高爐的實際運行輸出之間的誤差及其變化率，運用模糊邏輯推理，擬合各個工況的權值，并由此來加權各個工況下的模型以得到復合預測模型，再根據復合模型的預測輸出與高爐實際輸出之間的差值及其變化率在線修正3個模型的權值。

模糊控制是以模糊集合論、模糊語言以及模糊邏輯推理為基礎的計算機智能控制，其基本概念是由Zadeh首先提出的，經過20多年的發展，模糊控制在理論研究和實際應用方面都取得了重大發展[12-14]。

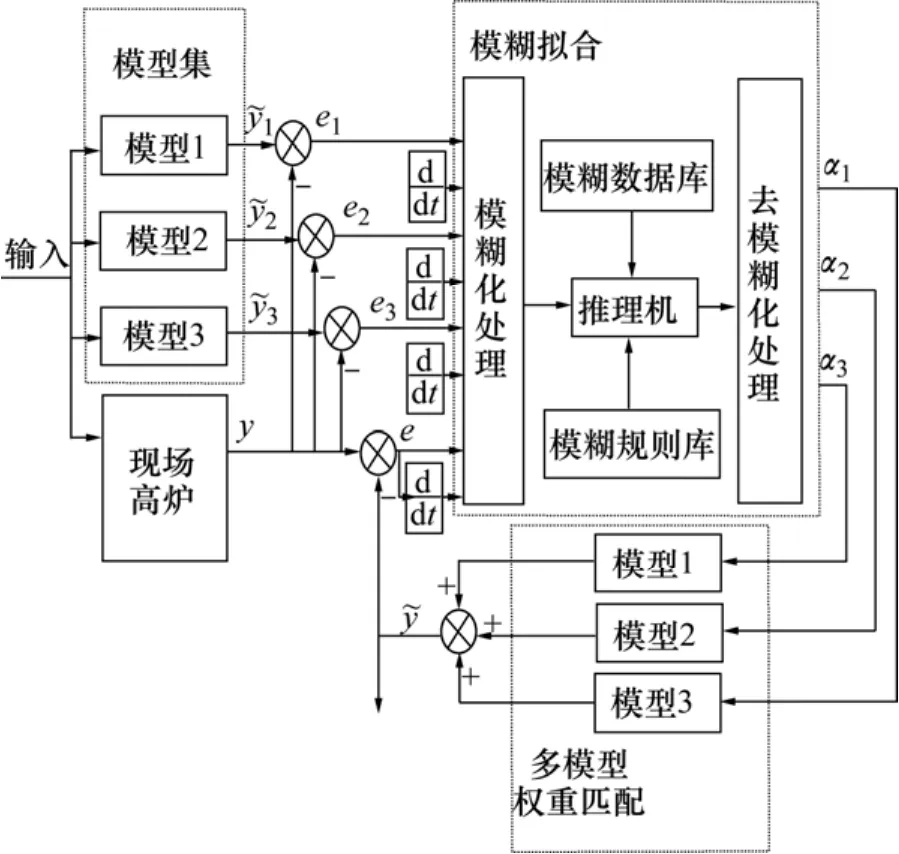
圖6 模型復合的推理過程Fig.6 Reasoning process of ally models

3.1 模糊化

當前系統的輸入進入到各個單模型，得到各單模型的預測輸出，模糊推理的輸入分別為3個模型的輸出誤差及誤差變化率，還有復合模型的輸出誤差和誤差變化率；模糊推理的輸出為3個模型的權重系數。下面為輸入和輸出的模糊化分割方式：

(1) |e|表示誤差絕對值，選用3個語言變量S，M和B分別代表誤差的小、中、大；

(2) e˙，即 de/dt，反映|e|的變化率和變化方向，分別用NB，NM和NS以及PS，PM和PB代表誤差的負大、負中、負小和正小、正中、正大；

(3) 輸出量α指的是各模型的權重系數，分別用S，M和B代表各模型與當前工況的匹配程度為不好、一般和好。

選擇各變量的隸屬度函數為均勻三角函數，根據各變量的隸屬度函數，可以近似得出各個語言變量的賦值。

3.2 模糊擬合推理

模糊擬合推理是一種不確定性推理方法，其基礎是模糊邏輯，它是要找出在不同時刻3個模型權重參數與各個誤差以及誤差變化率之間的模糊關系，在運行中不斷檢測|e|和e˙，根據模糊推理規則對 3個權重系數進行在線修改，以滿足控制精度的要求。因此，對這3個權重的整定可以考慮如下：

(1) 當|e1|，|e2|和|e3|中有1個很小，而另外2個很大時，說明誤差很小的模型與當前工況匹配程度較高。

(2) 當|e1|，|e2|和|e3|中有2個較小，而另外1個較大時，說明系統當前工況介于誤差較小的2個模型之間。此時則要根據復合模型的輸出誤差和2個誤差較小的模型的誤差變化率共同決定模型匹配度。

(3) 當|e1|，|e2|和|e3|中某個量超過基本論域范圍，就說明其對應的模型誤差太大，不適合當前工況，則自動將其權重設置為小。

根據這些調整原則以及高爐專家的經驗，可以得到相應的模糊規則，形式如下：

3.3 去模糊化

由于重心法對于輸入的微小變化推理的最終輸出一般都會發生一定的變化并且這種變化比較平滑，故模糊擬合的去模糊化算法采用重心法，取模糊隸屬度函數曲線與橫坐標圍成的面積的重心為模糊推理的最終輸出。

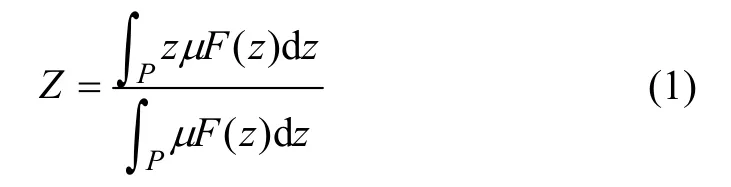
其中：P為輸出論域；F為其模糊子集。

3.4 權重在線修正

在實際運行中，系統根據當前輸入與模糊修正規則得到各模型權重1α，2α和3α，從而得到復合模型輸出

將復合模型輸出與系統實際輸出之間的誤差e及其變化率e˙模糊化后與已經建立好的模糊規則一起在線調整各權重值，假設1α比較大，2α比較小，3α也比較小，同時e比較小且有減小趨勢，說明1α對應的工況比較符合當前的運行情況，則繼續增大1α，可用下面的模糊修正規則來表達。

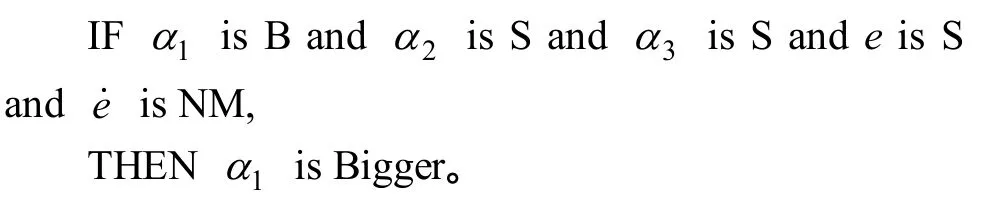
3.5 模糊推理結果

將此模糊擬合推理用來生成本高爐3個單模型的權重，進而建立復合模型。圖7所示為取介于低溫與適溫之間的歷史數據進行驗證的結果，顯示了復合模型的預測結果。

從圖7可以看出：復合模型預測誤差比較小，能夠穩定在7.5%以內，滿足精度要求。為增強系統的適應性，實際運行時，需要不斷評估所建立的模型是否包括了高爐運行的所有狀況，如果沒有，則根據出現的情況，建立新模型，加入系統參與預測，以此不斷完善系統。

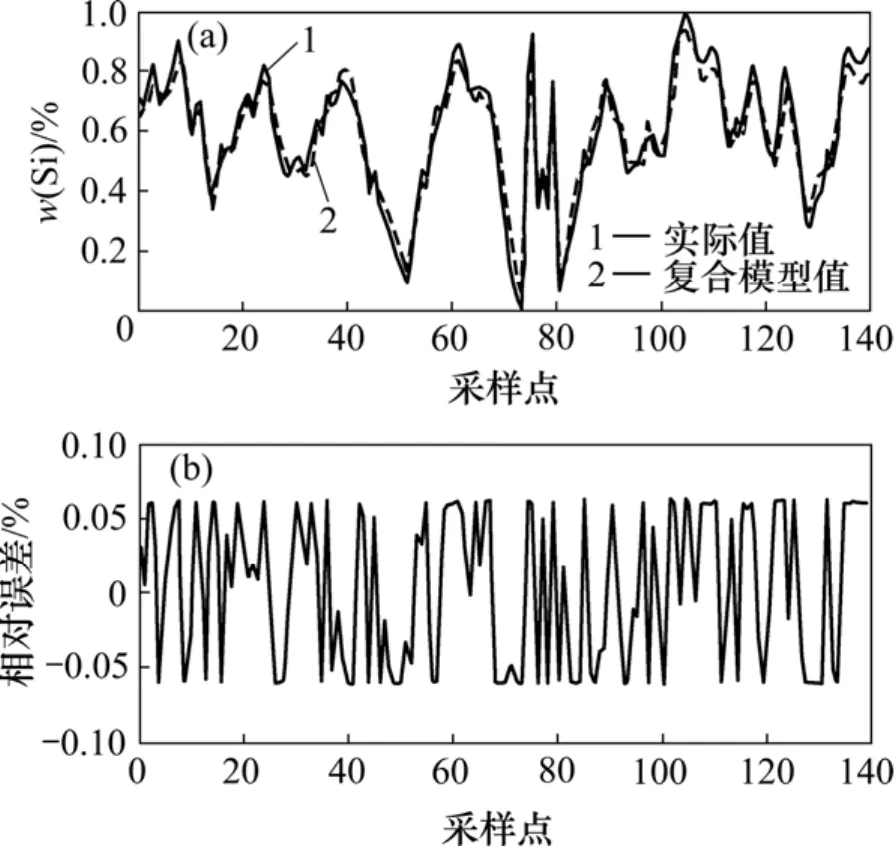
圖7 復合模型預測結果Fig.7 Final regression result

4 結果驗證

4.1 單模型與復合模型的結果對比

為了對本文所得到的智能復合模型的預測精度進行驗證，選取了5組歷史數據。這5組數據分別為高、中、低溫3個工況下的數據，以及介于高、中溫和中、低溫之間的數據。對于這5組數據，分別用單模型和復合模型進行預測，將得到的預測結果進行對比，結果如圖8～10所示。

圖8 低溫時2種模型的輸出誤差對比Fig.8 Output-error of two models at low temperature

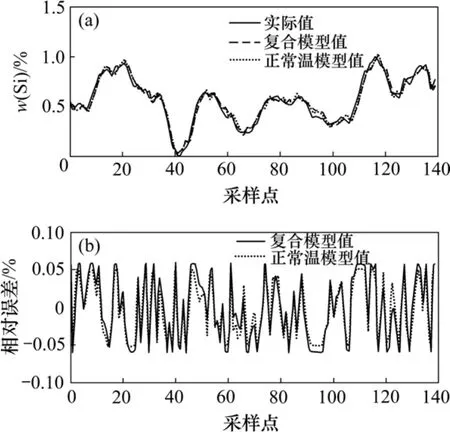
圖9 正常溫度時2種模型的輸出誤差對比Fig.9 Output-error of two models at normal temperature

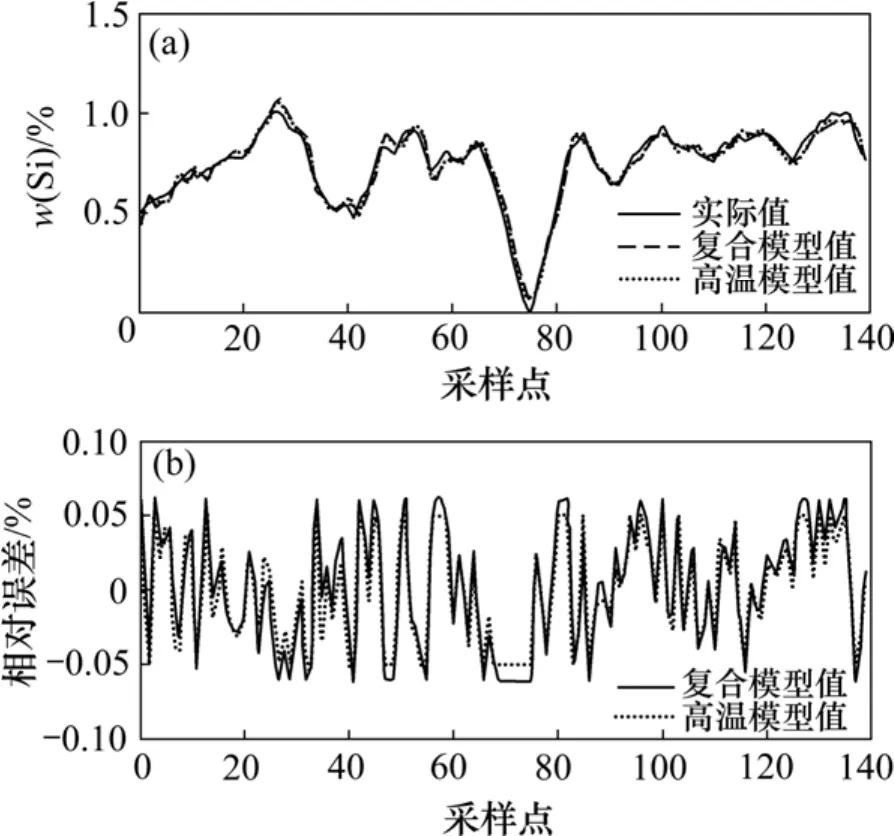
圖10 高溫時2種模型的輸出誤差對比Fig.10 Output-error of two models at high temperature

正常溫度和高溫時，2種模型的輸出誤差對比結果分別如圖9～10所示。從圖9～10可以看出：復合模型對處于某特定工況的情況，擬合誤差雖然不及單模型，但是能夠滿足精度要求。

圖11和12所示分別為介于低中溫、中高溫時3種模型的輸出誤差對比。

從圖11和12可以看出：當實際運行情況介于某2種工況之間時，復合模型的擬合誤差比各單模型的要小。

圖11 介于低中溫時3種模型的輸出誤差對比Fig.11 Output-error of three models at lower temperature

圖12 介于中高溫時3種模型的輸出誤差對比Fig.12 Output-error of three models at higher temperature

4.2 復合模型與多模型的結果對比

目前對于多工況的工業控制研究比較多的是多模型。

多模型是根據系統歷史數據，分別獲得多個工況的模型，根據經驗設置開關函數，根據系統當前運行情況在多個單工況模型之間進行切換。

為了進一步驗證復合模型的有效性，選取一組包含了多個工況的數據，分別用傳統多模型和復合模型進行預測，結果如圖 13所示。從圖13可以看出：傳統多模型的誤差大于復合模型的誤差，特別是在工況波動較大的情況下，多模型的擬合精度遠小于復合模型的擬合精度。

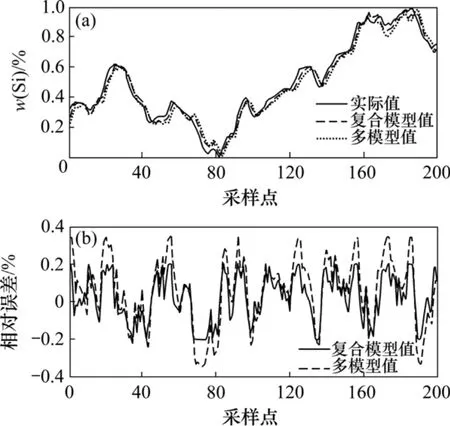
圖13 傳統多模型與復合模型的輸出誤差對比Fig.13 Output-error of multi-model and mixed model

5 結論

(1) 采用智能聯合預測模型，先建立不同工況下的鐵水硅含量多變量預測模型，然后運用模糊推理得到當前生產過程接近某個模型的程度，進行基于規則的多模型智能融合和在線調整，將各個模型與其權重乘積之和作為實際的預測輸出，并與傳統多模型進行比較。

(2) 建立的規則庫比較小，與直接運用傳統專家系統相比能夠有效降低搜索和匹配規則所用的時間，使計算周期縮短，預測迅速，對被控對象的變化有較強的魯棒性，實用性好。

(3) 與一般工業常用單模型或者多模型相比，此方法能夠軟化工況切換過程，提高工況切換過程的預測精度。

[1]張大尉, 高爐爐況預報專家系統的研究[D]. 合肥: 合肥工業大學電氣與自動化工程學院, 2005: 1-52.ZHANG Da-wei. The research of expert system for blast furnace situation forecast[D]. Hefei: Hefei University of Technology.School of Electrical Engineering and Automation, 2005: 1-52.

[2]劉祥官, 劉芳. 高爐煉鐵過程優化與智能控制系統[M]. 北京:冶金工業出版社, 2003: 1-270.LIU Xiang-guan, LIU Fang. Blast furnace ironmaking process optimization and intelligent control system[M]. Beijing:Metallurgical Industry Press, 2003: 1-270.

[3]宋建成. 高爐煉鐵理論與操作[M]. 北京: 冶金工業出版社,2005: 1-338.SONG Jian-cheng. Blast furnace theory and operation[M].Beijing: Metallurgical Industry Press, 2005: 1-338.

[4]Reid M, Spencer K. Use of principal components analysis (PCA)on estuarine sediment datasets: The effect of data pretreatment[J]. Environmental Pollution, 2009, 157: 2275-2281.

[5]Honda K, Ichihashi H. Fuzzy PCA-guided robust k-means clustering[J]. IEEE Transactions on Fuzzy Systems, 2010, 18(1):67-79.

[6]Vapnik V. The nature of statistical learning theory[M]. New York:Springer-Verlag, 1995: 1-88.

[7]張學工, 關于統計學習理論與支持向量機[J]. 自動化學報,2000, 26(l): 32-42.ZHANG Xue-gong. About statistical learning theory and support vector machine [J]. Acta Automatica Sinica, 2000, 26(l): 32-42.

[8]許建華, 張學工. 統計學習理論[M]. 北京: 電子工業出版社,2004: 1-594.XU Jian-hua, ZHANG Xue-gong. Statistical learning theory[M].Beijing: Electronic Industry Press, 2004: 1-594.

[9]包哲靜. 支持向量機在智能建模和模型預測控制中的應用[D].杭州: 浙江大學電氣工程學院, 2007: 1-109.BAO Zhe-jing. Application of support vector machine in intelligent modeling and model predictive control[D]. Hangzhou:Zhejiang University. College of Electrical Engineering, 2007:1-109.

[10]漸令. 支持向量機在高爐爐溫預報中的應用[D]. 杭州: 浙江大學數學系, 2006: 1-58.JIAN Ling. Application of SVM to predict silicon content in hot metal[D]. Hangzhou: Zhejiang University. Department of Mathematics, 2006: 1-58.

[11]董海榮, 高冰, 寧濱, 等. 基于模糊PID軟切換控制的列車自動駕駛系統調速制動[J]. 控制與決策, 2010, 25(5): 794-800.DONG Hai-rong, GAO Bing, NING Bin, et al. Fuzzy-PID soft switching speed control of automatic train operation system[J].Control and Decision, 2010, 25(5): 794-800.

[12]劉金琨. 先進PID控制和MATLAB仿真[M]. 北京: 電子工業出版社, 2004: 1-470.LIU Jin-kun. Advanced PID control and MATLAB Simulink[M].Beijing: Electronic Industry Press, 2004: 1-470.

[13]劉劍鋒, 劉友梅, 桂衛華, 等. 基于模糊預測控制的機車制動控制方法[J]. 中南大學學報: 自然科學版, 2009, 40(5):1329-1335.LIU Jian-feng, LIU You-mei, GUI Wei-hua, et al. Locomotive brake control method based on fuzzy predictive control[J].Journal of Central South University: Science and Technology,2009, 40(5): 1329-1335.

[14]許良瓊, 陸新江, 李群明. 模糊PID控制在電磁懸浮平臺中的應用[J]. 中南大學學報: 自然科學版, 2005, 36(4): 631-636.XU Liang-qiong, LU Xin-jiang, LI Qun-ming, Application of fuzzy PID control to electromagnetic suspension platform [J].Journal of Central South University: Science and Technology,2005, 36(4): 631-636.

[15]Milosavljevic C. General conditions for the existence of a quasi-sliding mode on the switching hyper plane in discrete variable structure systems[J]. Automation and Remote Control,1985, 46(3): 307-314.