礦井通風系統三維聯通巷道建模算法及其應用

黃俊歆 ，王李管，熊書敏，田峰，陳建宏

(1. 中南大學 資源與安全工程學院，湖南 長沙，410083；2. 湖南工學院 安全與環境工程系，湖南 衡陽，421001；3. 中鐵隧道勘測設計院有限公司 第五設計分院，天津 300133)

巷道是礦井通風系統圖中的主體元素，其空間位置關系復雜、縱橫交錯，在二維圖形系統中無論是單線圖還是雙線圖都無法直觀地表現這種復雜的空間交錯關系。但目前國內外的礦井通風系統三維建模技術均尚未成熟。最具代表性的產品為澳大利亞VENTSIM 公司開發的三維可視化礦井通風仿真系統Ventsim Visual，但該軟件中三維巷道也僅是采用非聯通建模技術[1]。為了能夠區分出巷道之間空間層位關系，人們習慣用雙線表示礦井通風系統的巷道。郝天軒等[2]介紹了利用ObjectARX在AutoCAD上進行二次開發，并對通風系統單線圖逐一進行偏移、打斷等操作，最終形成通風系統雙線圖的方法，能夠較好的表現雙線巷道及其空間層位關系，但必須依賴AutoCAD軟件。李鋼等[3]提出礦井通風系統可視化固定寬度巷道雙線處理，只能處理等寬度巷道的設計，且當結點與多于3個巷道關聯時，計算復雜，難以編程實現。文獻[4]提出自動架橋法及假雙線法實現了通風系統雙線圖的繪制，無需計算雙線坐標來實現通風系統雙線圖自動繪制，但其消隱部分的渲染工作開銷非常大。本文作者在研究礦井通風仿真系統三維可視化技術時，基于礦井通風系統拓撲關系自動建立和管理，在二維雙線巷道自動生成算法的基礎上進行擴展，提出了一種新的礦井通風系統三維聯通巷道建模算法即多層閉合輪廓線聯合法(Combining multi-layer closed contour lines algorithm，CMCA)，該算法具有普適性、計算量小，執行效率高等特點，能夠真實地表現巷道的幾何形態及其空間的復雜交錯關系。該算法已應用于DIMINE數字礦山系統的三維礦井通風仿真模塊中[5-14]。

1 CMCA的基本原理

1.1 生成二維雙線巷道的基本原理

1.1.1 構建拓撲關系圖

礦井通風仿真系統中可以采用多種圖元表示通風系統單線圖，如直線、多段線、圓、圓弧，橢圓、橢圓弧、NURBS曲線等[15]。為便于闡述，以多段線表示巷道為例進行說明，對拓撲關系圖中各元素進行定義。

定義1 節點。多段線的實交點和端點對應于拓撲關系圖中的節點，以Ni表示節點；

定義2 有向弧。執行打斷操作后的通風系統單線圖中，每條多段線對應于拓撲關系圖中的2條方向相反的有向弧，其中與多段線方向相同的有向弧稱為正向弧，以Ai表示；與多段線方向相反的則稱為反向弧，以Ai′表示；

定義3 入弧。拓撲關系圖中任一實節點Ni，所有以節點Ni為末節點的有向弧稱為節點Ni的入弧；

定義4 出弧。拓撲關系圖中任一實節點Ni，所有以節點Ni為始節點的有向弧稱為節點Ni的出弧；

以一簡單角聯通風系統圖為例生成拓撲關系圖如圖1所示。提取通風系統單線圖中所有多段線，對其進行求交操作，得到若干實交點，在這些交點處將所有多段線打斷。為便于闡述，將其正向弧及反向弧分開畫在圖1(a)及圖1(b)中，拓撲關系圖由圖1所示的節點、正向弧、反向弧組成，稱為節點—正向弧—反向弧拓撲關系圖。

1.1.2 最外層閉合輪廓線

生成雙線巷道的關鍵是提取通風網絡拓撲結構圖中的閉合輪廓線。為正確生成通風系統雙線巷道圖，必須嚴格遵守最外層閉合輪廓線優先的搜索原則。

定義5 最外層閉合輪廓線。閉合輪廓線路徑經某節點Ni的1條入弧進入節點Ni，節點Ni有n條出弧，以該入弧為起點位置，繞節點Ni的沿逆時針方向進行搜索，搜索到的第1條未選出弧即為最外層閉合輪廓線的有向弧路徑。閉合輪廓線的提取過程中每個節點處都作該處理，最終提取的閉合輪廓線即為最外層閉合輪廓線。

1.1.3 閉合輪廓線的提取

提取閉合輪廓線時可從任一節點開始，若當前節點的入弧為空，則可選擇該節點的任一出弧為閉合輪廓線的當前有向弧。

嚴格遵守最外層閉合輪廓線優先的原則，提取

圖1所示拓撲結構圖中的所有閉合輪廓線，提取過程如下。

步驟1 取節點N3為起始節點，此時節點N3有3條出弧A3，A4及A5′，由于此時初始時節點N3的入弧為空，則可選擇節點N3的任意1條出弧為閉合輪廓線的當前有向弧，這里選擇A4，將A4加入閉合輪廓線鏈表中，同時將A4標記為已選。

步驟2 正向弧A4的末節點為N4，節點N4有 3條未選出弧A6，A2′及A4′，以入弧A4為起點沿逆時針搜索，搜索到的第一條出弧為A6，遵循最外層閉合輪廓線優先的原則，選擇A6作為閉合輪廓線的當前有向弧，將A6加入閉合輪廓線鏈表中，同時將A6標記為已選。

步驟3 正向弧A6的末節點為N5，節點N5有 3條未選出弧A5，A7及A6′，以入弧A6為起點沿逆時針搜索，搜索到的第一條出弧為A5，遵循最外層閉合輪廓線優先的原則，選擇A5作為閉合輪廓線的當前有向弧，將A6加入閉合輪廓線鏈表中，同時將A5標記為已選。此時閉合輪廓線經A5回到節點N3，完成一個閉合輪廓線的提取，閉合輪廓線如圖2(a)所示。

步驟4 任取一節點，這里仍選擇節點N3為下一閉合輪廓線的起始節點，此時N3只有2條出弧A3及A5′為未選。任取一出弧，這里選擇A3作為閉合輪廓線的當前有向弧。同理，提取當前閉合輪廓線為A3—A2—A4′，閉合輪廓線如圖2(b)所示。

步驟5 任取一節點作為下一閉合輪廓線的起始節點，此時任一節點均只有一條出弧為未選，所以惟一閉合輪廓線路徑提取為A1—A3′—A5′—A7—A7′—A6′—A2′—A1′。所有閉合輪廓線提取完畢。

圖1所示的通風網絡共可提取3個閉合輪廓線，如圖2所示。

1.1.4 閉合輪廓線的偏移

由于搜索算法采用逆時針搜索原則，故所有偏移操作采用右偏移方式，才能保證順、逆向閉合輪廓線分別向巷道中心線兩側偏移形成雙線巷道。上述3個閉合輪廓線分別向右偏移后所形成的雙線圖如圖 3所示。

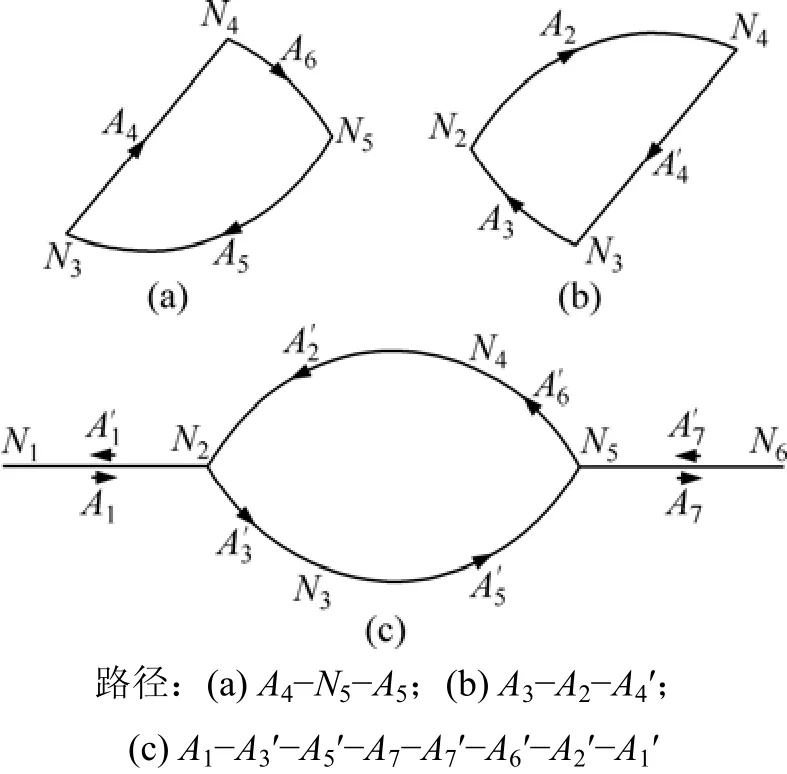
圖2 提取閉合輪廓線Fig.2 Pick up closed contour lines

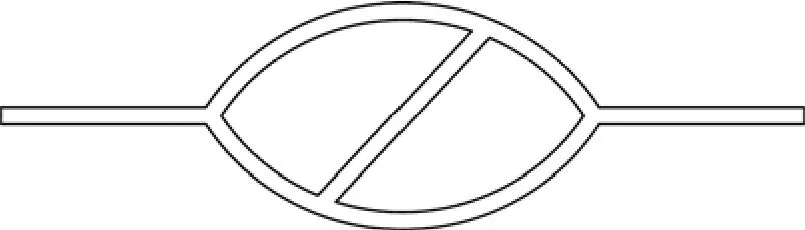
圖3 閉合輪廓線右偏移得到雙線巷道圖Fig.3 Double-line laneway graphic after right-offset

1.2 生成三維聯通巷道

生成三維聯通巷道的基本思想是：根據用戶輸入的生成精度，從巷道底部到頂部，插入若干與巷道底板平行的面，這些面與巷道相交形成一系列閉合輪廓線。將這些閉合輪廓線三角化，并合并所有三角網格來生成三維聯通巷道。

1.2.1 生成多層閉合輪廓線

以拱形巷道為例，其巷道斷面如圖 4(a)所示。從該斷面底部到頂部插入若干平面，與巷道斷面相交形成一系列交點，這些交點在相應平面上到中心線間的距離為Ln(0≤n≤19)，即為該平面上閉合輪廓線的偏移距離，頂部閉合輪廓線退化成1條線。再根據上述生成二維雙線巷道的方法，逐層生成閉合輪廓線，所有閉合輪廓線的結果如圖4(b)所示。

1.2.2 巷道三維建模

采用上述生成二維雙線巷道的算法，對每一層生成一組閉合輪廓線。得到多層閉合輪廓線后，巷道三維建模問題就轉化成多邊形的三角剖分問題。

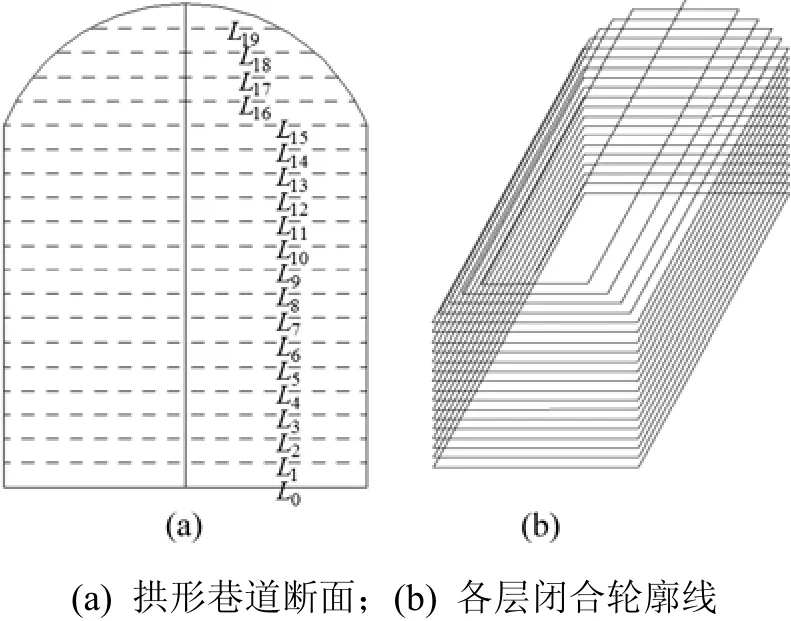
圖4 生成拱形巷道多層閉合輪廓線Fig.4 Closed contour lines of arch shape laneway

多邊形的三角剖分就是在不產生新頂點的條件下將平面多邊形劃分成一系列不相重疊的三角形[16]。多邊形三角剖分的算法很多，如 Gareym 等[17]提出的Sweep Line algorithm算法；Seidel[18]提出的Incremental Randomized算法等。這些算法較難擴展到帶洞多邊形的情況。Incremental randomized算法性能較好，但未見實現方面的報道；Chazelle[19]證明了多邊形的三角剖分可以在O(n)級時間內完成，但這種算法的實現非常困難[20]；李學軍等[21]提出的快速算法只是在單調多邊形三角化時的時間復雜度為O(n)，而在多邊形單調化時復雜度比O(n)要高，同時對含有島的多邊形是否支持還有待于進一步驗證；劉海濤等[22]提出的算法是將凹邊形分解成凸多邊形，再通過添加輔助點的方式對子多邊形進行三角剖分，時間復雜度為O(jn+nlogn+jklogn)；畢林等[23]提出的快速多邊形區域三角化算法，適合于帶有洞、島的任意簡單多邊形，速度近似為O(n)，且實現簡單。本文選用畢林等[23]所提出的算法實現了各層輪廓線的三角化并將所有的三角化網格合并，最終生成封閉的三維巷道實體表面模型。

顯然，在其他領域對于實體的聯通建模問題通常采用多邊形的三角剖分算法來實現，該算法目前已較為成熟。因此礦井通風系統三維聯通巷道的建模難點就在于多層閉合輪廓線的提取與生成。

2 CMCA實現算法

2.1 建立節點—正向弧—反向弧拓撲關系圖

為記錄通風系統圖的節點—有向弧—反向弧拓撲關系圖。構建數據結構如下，以類C語言描述為：Struct CNode

{

C3DPoint m_Pt; //交點的位置

CArcList m_Arcs; //以m_Pt為起點的有向弧鏈表

};

struct CArc

{

CCurve* m_pCurve; //對應的多段線

CArc* m_pRArc; //對應的反向弧

CNode* m_pSNode; //始節點

CNode* m_pENode; //末節點

Bool m_bClosed; //是否自閉合

double m_offset; //偏移距離(巷道寬度的1/2)

}；

該過程的主要為多段線相交或自相交求交點的操作，算法中以參數曲線[15]表示多段線。各交點對應于相應多段線上的一個參數坐標[15]，將各條多段線上的交點參數坐標從大到小排列，并按順序打斷成多條多段線。打斷后的每條多段線對應于2條有向弧，以數據結構 CArc記錄；各有向弧的端點稱為節點，以數據結構CNode記錄。

2.2 提取閉合輪廓線

提取閉合輪廓線為本算法的關鍵步驟，嚴格遵守最外層閉合輪廓線優先的原則提取節點—有向弧—反向弧網絡拓撲結構，設計算法如下：

第1步：在節點數組中任取一節點，以指針pNode指向該節點；

第2步：若pNode為空，閉合輪廓線提取完畢，程序結束；

第3步：若pNode的未選出弧數為0，指針pNode移至下一節點；

第4步：若當前閉合輪廓線鏈表為空，令閉合輪廓線鏈表頭指針pHeader=pNode；

第5步：將節點pNode加入到當前閉合輪廓線鏈表尾部；

第6步：若pHeader==pNode，任取pNode的一條出弧，令有向弧指針pArc指向該弧，并標記為已選；

第7步：以節點pNode為中心點，pArc為起始位置，沿逆時針方向搜索pNode的出弧，搜索到其第一條出弧為當前弧，令pArc指向該弧，并標記pArc為已選；

第8步：令pNode=pArc-＞m_pENode；

第9步：若pHeader==pNode，當前閉合輪廓線提取完畢，存儲當前閉合輪廓線，并清空當前閉合輪廓線鏈表跳轉至第1步提取下一閉合輪廓線。否則跳轉至第5步。

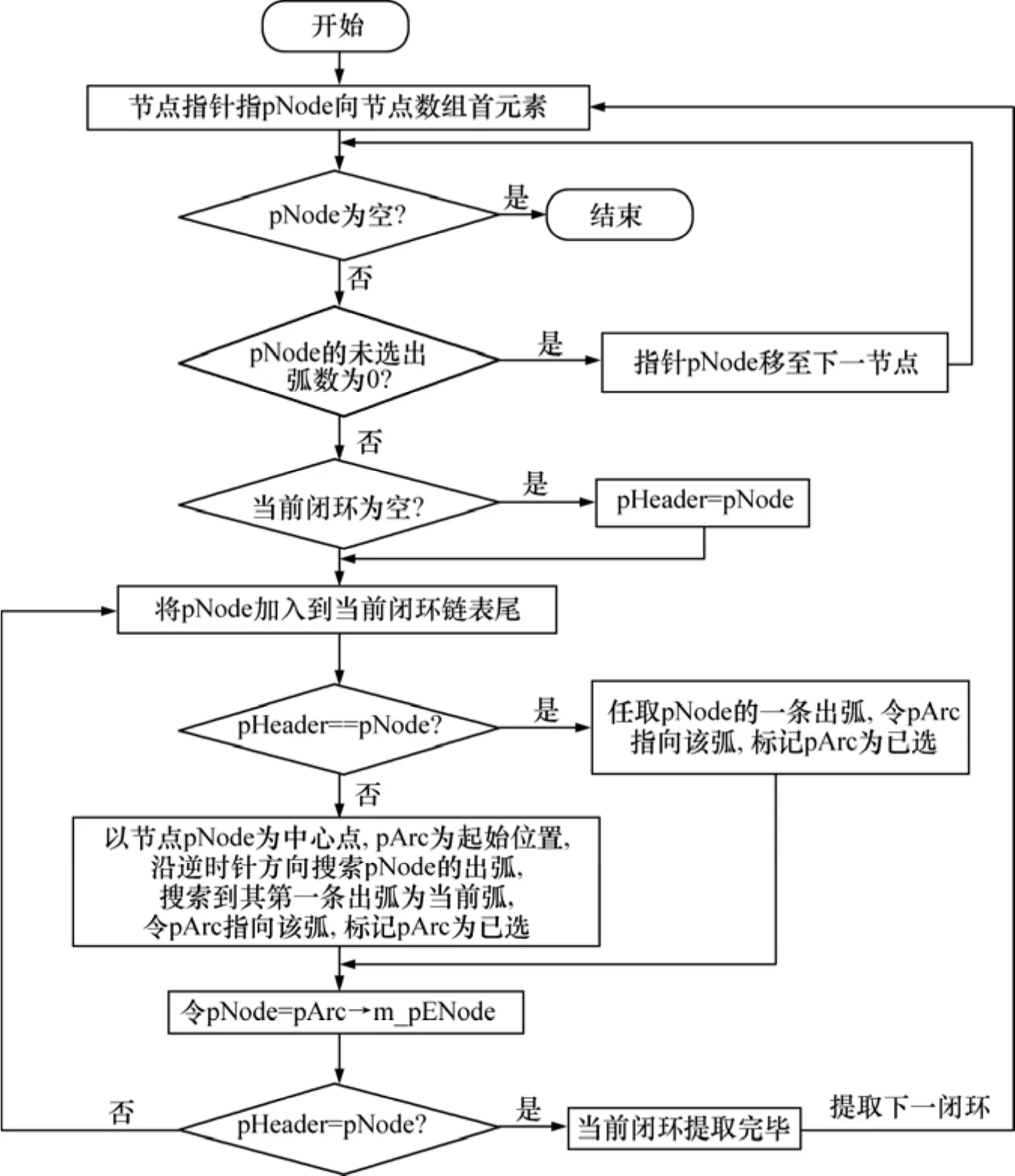
圖5 提取閉合輪廓線的算法流程圖Fig.5 Algorithm flow chart of pick up closed contour lines

圖5所示為提取一層閉合輪廓線的算法流程圖，其他各層閉合輪廓線的生成只需對其高程及寬度進行適當的調整即可。

2.3 閉合輪廓線右偏移

由于提取閉合輪廓線時采取最外層閉合輪廓線優先，且搜索策略為逆時針搜索。因此，所有閉合輪廓線采用右偏移，從而形成礦井通風雙線圖。目前偏移算法已非常成熟[15]。

2.4 生成三維巷道模型

得到各層閉合輪廓線后，利用文獻[23]中的快速多邊形區域三角化算法，將各層輪廓線三角化并將所有的三角網格合并，最終生成封閉的三維巷道實體表面模型。具體的實現方法參見文獻[23]。

3 實例應用

以圖1所示的簡單角聯通風網絡為例。將A1的斷面設為圓形，A2，A3，A5，A6的斷面設為圓弧拱，A4的斷面設為梯形，A7的斷面設為矩形。采用本文提出的算法對其建立聯通巷道模型，如圖6(a)所示，為觀察其內部聯通狀況，從巷道中部進行剖切，剖面圖如圖6(a)所示。

圖6 簡單角聯通風網絡三維聯通巷道模型Fig.6 3D-interconnected laneway model of simple diagonal ventilation network

4 結論

(1)礦井通風系統三維聯通巷道的建模難點在于多層閉合輪廓線的提取與生成。

(2)充分利用礦井通風系統單線圖的節點—正向弧—反向弧網絡拓撲結構圖，采用最外層閉合輪廓線優先的逆時針搜索方法，通過在巷道頂底板間插入若干與巷道底板平行的面，從而得到多層閉合輪廓線。

(3)提出了多層閉合輪廓線聯合法(CMCA)，在提取上述多層閉合輪廓線的基礎上生成三維聯通巷道表面模型。

(4)如何提高通風系統單線圖中各多段線求交的運算及后期三角剖分運算的效率，進一步減少數據前期處理的運算量，是今后算法優化的主要方向。

[1]Ventsim L T D. Ventsim Visual? User Guide[EB/OL].[2009-12-01]. http://www.ventsim.com/Manual.htm.

[2]郝天軒, 李輝, 魏建平, 等. 礦井通風系統平面圖自動繪制系統的研制[J]. 中國煤炭, 2005, 31(3): 28-30.HAO Tian-xuan, LI Hui, WEI Jian-ping, et al. Research on mine ventilation plan automatic drawing system [J]. China Coal, 2005,31(3): 28-30.

[3]李鋼, 陳開巖, 聶百勝. 礦井通風系統 CAD 技術研究[J]. 遼寧工程技術大學學報, 2005, 24(6): 636-638.LI Gang, CHEN Kai-yan, NIE Bai-sheng. Research on CAD technology in mine ventilation system[J]. Journal of Liaoning Technical University, 2005, 24(6): 636-638.

[4]李鋼, 陳開巖, 何學秋, 等. 礦井通風系統巷道自動繪制方法研究[J]. 煤炭科學技術, 2006, 34(6): 797-800.LI Gang, CHEN Kai-yan, HE Xue-qiu, et al. Research on laneway auto mapping method for mine ventilation system[J].Coal Science and Technology, 2006, 34(6): 797-800.

[5]倪景峰. 礦井通風仿真系統可視化研究[D]. 阜新: 遼寧工程技術大學安全科學與工程學院, 2004: 5-25.NI Jing-feng. The study on visualization of mine ventilation simulation[D]. Fuxin: Liaoning Technical University. School of Safety Science and Engineering, 2004: 5-25.

[6]牛永勝, 曹榮, 陳學習, 等. 礦井通風三維可視化仿真系統的設計與實現[J]. 金屬礦山, 2007, 373(7): 73-76.NIU Yong-sheng, CAO Rong, CHEN Xue-xi, et al. Design and implementation of 3D visualized simulation system of mine ventilation[J]. Metal Mine, 2007, 373(7): 73-76.

[7]黃光球, 陸秋琴, 鄭彥全. 存在固定風量分支的通風網絡解算新方法[J]. 金屬礦山, 2004(10): 52-54.HUANG Guang-qiu, LU Qiu-qin, ZHENG Yan-quan. A new optimization algorithm for ventilation network with fixed volume branches[J]. Metal Mine, 2004(10): 52-54.

[8]魏連江, 王德明, 王琪, 等. 構建礦井通風可視化仿真系統的關鍵問題研究[J]. 煤礦安全, 2007, 392(7): 6-9.WEI Lian-jiang, WANG De-ming, WANG Qi, et al. Study on some key issues of constructing visual mine ventilation simulation system[J]. Safety in Coal Mines, 2007, 392(7): 6-9.

[9]魏連江, 朱華新, 張雷林. 礦井通風仿真系統雙線圖的快速自動繪制研究[J]. 中國安全科學學報, 2008, 18(11): 55-59.WEI Lian-jiang, ZHU Hua-xin, ZHANG Lei-lin. Study on the rapid automatic drawing of double-line diagram of mine ventilation simulation system[J]. China Safety Science Journal,2008, 18(11): 55-59.

[10]王德明, 李永生. 礦井火災救災決策支持系統的研究[M]. 北京: 煤炭工業出版社, 1996: 14-44.WANG De-ming, LI Yong-sheng. Study of mine fire rescue decision support system[M]. Beijing: Coal Industry Press, 1996:14-44.

[11]蘇清政, 劉劍. 礦井通風仿真系統理論與實踐[M]. 北京: 煤炭工業出版社, 2006: 24-40.SU Qing-zheng, LIU Jian. The theory and practice of mine ventilation simulation system[M]. Beijing: Coal Industry Press,2006: 24-40.

[12]倪景峰, 劉劍. 礦井通風系統可視化固定寬度巷道雙線處理[J]. 遼寧工程技術大學學報, 2005, 24(5): 28-30.NI Jing-feng, LIU Jian. Fixed distance double line automatic treatment of tunnel coordinates in mine ventilation visualization[J]. Journal of Liaoning Technical University, 2005,24(5): 28-30.

[13]魏連江, 王德明. 基于構件的礦井通風安全管理系統的開發研究[J]. 中國礦業, 2006, 15(12): 25-27.WEI Lian-jiang, WANG De-ming. Study on the mine ventilation and safety management system developments base on component[J]. China Mining Magazine, 2006, 15(12): 25-27.

[14]魏連江, 郝憲杰, 張宏捷, 等. 礦井通風仿真系統區分井巷層位關系的新方法研究[J]. 金屬礦山, 2008, 384(6): 105-107.WEI Lian-jiang, HAO Xian-jie, ZHANG Hong-jie, et al. Study on new methods for identifying tunnel layer relationship in mine ventilation simulation system[J]. Metal Mine, 2008, 384(6):105-107.

[15]Philip J S, David H E. 計算機圖形學幾何算法工具詳解[M].北京: 電子工業出版社, 2005: 6-20.Philip J S, David H E. Geometric tools for computer graphics[M].Beijing: Publishing House of Electronics Industry, 2005: 6-20.

[16]馬小虎, 潘志庚, 石教英. 基于凹凸頂點判定的簡單多邊形Delaunay三角剖分[J]. 計算機輔助設計與圖形學學報, 1999,11(1): 1-3.MA Xiao-hu, PAN Zhi-geng, SHI Jiao-ying. Delaunay triangulation of simple polygon based on determination of convex concave vertices[J]. Journal of Computer Aided Design& Computer Graphics, 1999, 11(1): 1-3.

[17]Gareym R, Johnson D S, Preparata F P, et al. Triangulating a simple polygon[J]. Information Proceeding Letters, 1978, 7(4):175-179.

[18]Seidel R. A simple and fast incremental randomized algorithm for computing trapezoidal decompositions and for triangulating polygons[J]. Comput Geom Theory Appl, 1991, 1(1): 51-64.

[19]Chazelle B. Triangulating a simple polygon in linear time[J].Discrete Comp Geom, 1991, 6(5): 485-524.

[20]WU Liang. Fast and robust simple polygon triangulation with/without holes by sweep line algorithm[EB/OL].[2007-03-18].http://www.mema.ucl.ac.be/～wu/Poly2Tri/poly2tr i.Html

[21]李學軍, 黃文清. 平面區域三角化的快速算法[J]. 計算機輔助設計與圖形學學報, 2003, 15(2): 233-238.LI Xue-jun, Huang Wen-qing. Fast triangulation algorithm for planar regions[J]. Journal of Computer Aided Design &Computer Graphics, 2003, 15(2): 233-238.

[22]劉海濤, 張三元, 葉修梓. 一種快速相容三角剖分算法[J]. 計算機應用研究, 2007, 24(1): 235-237.LIU Hai-tao, ZHANG San-yuan, YE Xiu-zi. Fast compatible triangulations algorithm[J]. Application Research of Computers,2007, 24(1): 235-237.

[23]畢林, 王李管, 陳建宏, 等. 快速多邊形區域三角化算法與實現[J]. 計算機應用研究, 2008, 25(10): 3030-3033.BI Lin, WANG Li-guan, CHEN Jian-hong, et al. Fast triangulation algorithm for polygon regions and implementation[J]. Application Research of Computers, 2008,25(10): 3030-3033.