基于馬爾可夫鏈的自然風風向建模

季亮，譚洪衛(wèi)，王亮

(同濟大學 機械工程學院，上海，200092)

自然風是大氣運動的結果，其風向、風速時刻都在發(fā)生變化。對于和自然風相關的科研領域，自然風風速、風向變化的基礎數(shù)據(jù)和變化特征是至關重要的，例如：風能發(fā)電[1]，自然通風工程[2]，城市大氣環(huán)境評價[3]，污染物排放擴散預測[4]等研究領域。然而，相關研究常常將自然風風速和風向視作一個穩(wěn)態(tài)參數(shù)并選取某個時間段內平均風速和主導風向，以此作為邊界條件進行研究。這種恒定風的假設，可能會導致研究結果偏離客觀事實。因此，必須充分考慮風向和風速的動態(tài)變化。自然風動態(tài)變化的數(shù)據(jù)盡管可以通過氣象臺站的實測獲得，但該方法存在諸多限制：獲取實測數(shù)據(jù)耗費人力物力，也難免會存在數(shù)據(jù)缺失；實測的數(shù)據(jù)是歷史數(shù)據(jù)，對于預測評估而言存在不足；盡管氣象臺站的實測全年的動態(tài)變化數(shù)據(jù)，但時間尺度不完全符合要求，一般氣象臺站可以向社會公開公布的月平均數(shù)據(jù)，另外通過購買氣象產(chǎn)品可獲得逐時變化的數(shù)據(jù)，但對于更小時間尺度的數(shù)據(jù)如逐分變化的動態(tài)數(shù)據(jù)則難以獲得。對風向變化進行分析、基于數(shù)學方法對自然風進行數(shù)學建模，從而可以人工推演自然風變化尤為必要。國內外對自然風建模方法的基礎理論及其應用已進行許多研究。例如，芮曉明等[5-7]在風電領域對自然風風速變化模型展開研究，為風力發(fā)電能力預測提供指導；Sahin等[8]以一階馬爾可夫鏈為基礎，用土耳其實測的逐時風速序列，反演自然風風速的人工時間序列，證明盡管一階馬爾可夫鏈僅具有一階的相關性，但90%符合客觀風速分布，證實馬爾可夫鏈在風速建模過程中的有效性；Kantz等[9-11]基于馬爾可夫鏈的基本原理，以風速為研究對象，將自然風看作是隨機變量的時間序列，基于逐時測試數(shù)據(jù)，對自然風進行建模；Dobigeon等[12-13]考慮風向和風速的聯(lián)合相關性，然后進行自回歸建模，但其采用的樣本之間的時間跨度較大，而風向在這樣的時間跨度內是相對穩(wěn)定的，因而，其得到的風向模型仍是一個準靜態(tài)模型。總體上，國內外基于馬爾可夫鏈的基本原理，對自然風風向進行建模的研究較少，且在這些有限的研究中，沒有關注到更小時間尺度(如逐分)的風向變化，未能充分反映自然風風向的動態(tài)變化特征。本研究以小時間尺度的風向變化為研究對象，基于馬爾可夫過程的原理，求取一個36狀態(tài)的轉移矩陣，完整提出對風向進行建模并反向推演自然風風向變化時間序列的方法。同時，輔以上海中心城區(qū)的逐分實測得到自然風數(shù)據(jù)，獲得當?shù)氐霓D移概率矩陣模型。

1 馬爾可夫鏈模型

對于馬爾可夫鏈，在隨機過程等相關文獻中有詳細的闡述[14]。這里僅對本文用到的馬爾可夫鏈基本原理進行基本簡述。

馬爾可夫鏈的基本特征為：在給定當前信息的情況下，當前的狀態(tài)可以用來預測將來，過去的狀態(tài)對于預測將來狀態(tài)是無關的。

馬爾可夫鏈是隨機變量X1，X2，X3…的一個序列。這些變量的取值范圍，即所有可能的取值的集合，被稱為“狀態(tài)空間”。根據(jù)馬爾可夫鏈原理，Xn+1取得某狀態(tài)的概率僅和Xn相關，即：

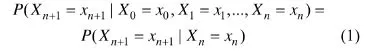
其中：P(·)表示概率函數(shù)；Xi為時間序列的第i個隨機變量；xi為第i個隨機變量的狀態(tài)值。

該等式的含義是：當Xn的狀態(tài)值是xn時，第Xn+1的狀態(tài)值為xn+1的概率是一定的，且僅和Xn相關。

2 基于馬爾可夫鏈的自然風風向的建模方法

馬爾可夫鏈是常用的隨機過程之一，但針對風向建模較為少見，且對本文所關注的小時間尺度風向建模而言，有2個新特點：首先是風向的狀態(tài)空間和風速不同，風向狀態(tài)空間是一個360°圓周角中的值，將某一個風向角設定為固定的狀態(tài)是不合理的；其次對小時間尺度而言，自然風風向的波動特性明顯，而不像較大時間跨度情況下風向較為穩(wěn)定。因此，小時間尺度的狀態(tài)變化程度會顯著高于大時間尺度。

自然風風向建模包含2個方面 (如圖1所示)：首先應當根據(jù)當?shù)貧v史數(shù)據(jù)和馬爾可夫鏈提出的風向建模方法，構建當?shù)仫L向變化的轉移概率模型；其次，根據(jù)獲取的概率轉移模型，反向推演，以預測當?shù)氐娘L向變化。

圖1 風向建模的流程Fig.1 Flow chart of wind direction modeling

2.1 以馬爾可夫鏈對自然風風向建模的步驟

2.1.1 確定狀態(tài)空間

自然風風向具有的最主要特點是：在一定的時間跨度內具有一個主導風向，即該風向出現(xiàn)的頻率最高，總持續(xù)時間最長。因此，將主導風向定義為狀態(tài)值0。并以此為基礎，每順時針增加10°就將狀態(tài)值取值加1，每逆時針增加10°就將狀態(tài)值取值減1，這樣，在360°的圓周角范圍內共有36個狀態(tài)值。表1所示為風向的狀態(tài)空間。

2.1.2 風向的轉移概率模型

對某個時刻而言，該時刻有可能取得其狀態(tài)空間中的任何狀態(tài)，只是取得各不同狀態(tài)的概率不同，根據(jù)前述內容，后一個時刻達到某狀態(tài)的概率與前一個時刻的狀態(tài)有關，該特性可以表示為式(2)。其取得所有狀態(tài)值的概率的和為1，可以表示為式(3)。

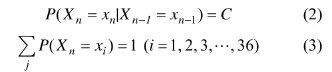
其中：C為一個常數(shù)；Xn和Xn-1分別為第n個和第n-1個時刻的狀態(tài)；xi為第i個狀態(tài)。在本文中，共定義36個狀態(tài)，因此，xi有36個取值。

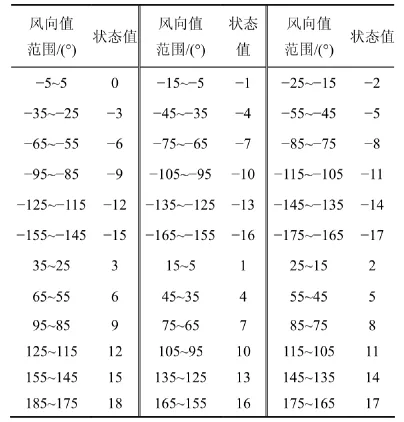
表1 各風向角度狀態(tài)值Table1 Status value of wind direction

基于馬爾可夫鏈的這種性質，可以定義一個“轉移概率矩陣”。該矩陣表示當前一個時刻取值xi時，后一個時刻取值xj的概率。矩陣中的每一個元素均表示一個轉移概率。用Pij來表示轉移矩陣中的1個元素，則Pij可表示為式(4)，轉移矩陣可以表示為P(式(5))。

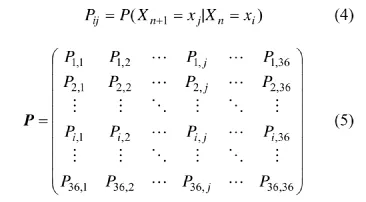
其中：Pij從當前的狀態(tài)i到下一個狀態(tài)j的概率；P轉移概率矩陣。

對于P，可通過分析歷史的實測樣本數(shù)據(jù)求得。到此，已經(jīng)完成對自然風風向變化的建模。轉移概率矩陣P中的任意1個元素，表示當前時刻的風向值與下一個時刻的風向值的條件概率關系。因此，P以轉移概率的方式，建模并表達自然風風向變化。

2.2 基于轉移概率模型對風向進行反演和預測

2.2.1 基于轉移矩陣求取疊加轉移矩陣

根據(jù)式(3)，對P中的任何一行均有下式成立：

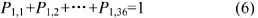
據(jù)此，對P按照式(7)進行轉化，使之成為P′(為便于區(qū)分，用k和l分別表示新矩陣P′的行和列的編號)。將P′稱為P的“疊加轉移矩陣”。

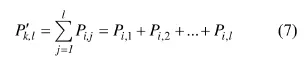
矩陣P′的物理意義是：P′中任意一行第N個元素的值是P中該行的第1列元素到第N個元素的和。易知P′的最后一列均是1。

2.2.2 耦合疊加轉移矩陣和隨機數(shù)，以主導風向反演風向動態(tài)變化時序列

根據(jù)疊加轉移矩陣本身的特點，即可通過計算機隨機數(shù)來反向推演風向時間序列。

為便于分析，假定風向只有4個狀態(tài)，其狀態(tài)值分別為1，2，3和4(分別代表東、南、西、北4個風向)。

首先通過當?shù)匾延械臍v史數(shù)據(jù)得到轉移矩陣P。假設P為：

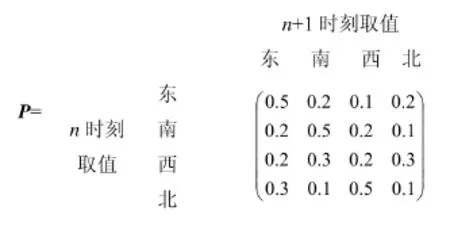
矩陣P更加直觀地說明轉移矩陣的意義。如，當Xn時刻出現(xiàn)了東風時，那么，Xn+1時刻出現(xiàn)東風的概率為0.5，出現(xiàn)南風和北風的概率為0.2，出現(xiàn)其完全反方向的風(西風)的概率為0.1。矩陣P的疊加轉移矩陣則為：

假定當日的主導風向為南風，則令初值X1=2(南風)，通過計算機隨機生成1個介于0到1之間的隨機小數(shù)，假定此值為0.392。那么，對第2行而言，該值落在第1個元素和第2個元素之間。因此，可以認為下一個時刻(X2)的狀態(tài)值轉移為第2列所表達的狀態(tài)(仍然是南風)。然后，將X2=2(南風)作為初始值，以相同方法求取X3。依此類推，直到求取到指定的時間長度Xn。

2.3 馬爾可夫過程對自然風進行建模與反演的合理性分析

耦合隨機數(shù)和基于馬爾可夫鏈原理的轉移矩陣的合理性在于：一方面，計算機隨機數(shù)本身是0到1之間一個平均分布；另一方面，轉移矩陣則體現(xiàn)當前狀態(tài)對下一狀態(tài)的影響程度，轉移矩陣中的任何1個元素Pij代表從狀態(tài)xi到狀態(tài)xj可能性，因此，轉移矩陣體現(xiàn)狀態(tài)之間相互轉移的概率，體現(xiàn)變化的權重程度。隨機值的平均分布體現(xiàn)所有可能的狀態(tài)空間，而轉移矩陣則反映狀態(tài)值轉移的不同可能性。這2個不同的分布函數(shù)的結合使用，完整地重現(xiàn)自然風時序列的物理意義，因此，該方法是合理、有效的。

3 實例應用：上海中心城區(qū)風向建模

以下基于上海地區(qū)小尺度連續(xù)采樣的實測數(shù)據(jù)，為上海城區(qū)的風向變化進行建模。建立測點對上海中心城區(qū)風向進行長期高頻采集。以1 min為樣本取樣間隔，在上海中心城區(qū)某高樓的頂部設立小型氣象站(超聲波流量計)連續(xù)計測自然風數(shù)據(jù)。方圓350 m內，均無高于該樓的建筑，可認為無論風向從何而來，測點均不處于其他建筑的繞流區(qū)內。

3.1 用于求取馬爾可夫鏈的時序列樣本簡介及處理

在進行建模之前，首先必須對風向本身的變化特征進行系統(tǒng)分析，從而能對樣本進行優(yōu)化。為便于展示，下面選取大量測試數(shù)據(jù)中具有代表性的一段，對自然分風向變化特征進行說明(見圖2和圖3)。

從圖2和圖3可見自然風風向的基本變化特征如下：(1)逐時主導風向在一段時間內較穩(wěn)定；(2)逐分的風向則時刻都在隨機變化；(3)風向主要在當日主導風向兩側較小的范圍內小幅度變化。需要說明的是：在圖2中第840 min至第1 080 min的時間段內的變化，容易產(chǎn)生風向變化幅度增大的誤解，但因為Y軸的物理量是圓周角，圖2中的-180°和+180°之間的風向差值并非360°，而是0°，因此，風向變化幅度仍然是小幅度的。

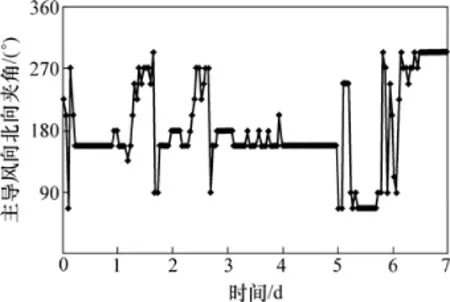
圖2 1周內的逐時風向變化圖Fig.2 Hourly variation of wind direction for a week

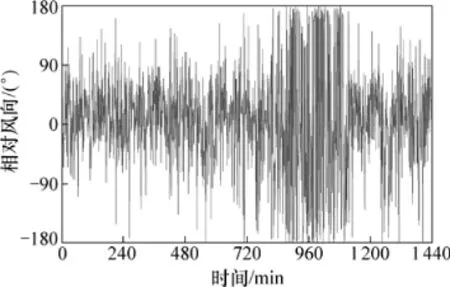
圖3 1日內逐分風向變化圖Fig.3 Minutely variation of wind direction with day

由于存在上述特征，在進行風向建模前，首先對自然風風向進行“分段中心化處理”，即將所有的的測試樣本按照主導風向不同分為不同的時間段；其次，將所有的時間段以當段內的主導風向為中心，求取其“相對”夾角，而非測試儀器測量得到的“北向夾角”，并將“相對夾角”的數(shù)據(jù)全部重新連接成隨機序列。

這樣處理后的樣本，可消除大氣環(huán)流導致的風向變化(這種風向變化是和地球公轉、自轉運動的結果)帶來的影響，而關注本文所研究的焦點是小時間尺度的隨機變化。根據(jù)上述分析和“中心化”后，本文共在6個月的測試數(shù)據(jù)內獲得大約900 000個逐分的時序列樣本，測試時間跨度是上海地區(qū)的2009年10月20日至2010年4月10日。

3.2 自然風風向建模及反演風向時序列

采用前面所述的方法，基于處理后的時序列樣本，構建上海地區(qū)的風向變動轉移概率矩陣模型(如圖4所示)。由于頁面尺寸限制，圖4中的轉移概率矩陣僅表示2位有效數(shù)字。然后，以該轉移概率矩陣為基礎，進行反向推演分析，推演結果如圖5所示。

從圖5可見：人工反演的自然風風向，其振幅和變化范圍均與實測值接近。經(jīng)過統(tǒng)計計算，反演的時間序列樣本和實測時序列樣本的均值、方差、頻率分布(見圖6)非常接近，其中：實測樣本的均值為285.7°，標準差為24.5°；反演樣本的均值為285.8°，標準差為23.5°；各風向分布直方圖如圖6所示。

由圖6可見：該方法得到的風向變化時序列的統(tǒng)計特性和歷史數(shù)據(jù)具有良好相似性，且充分反映動態(tài)變化，對預測未來風向變化，從而將其應用于其他學科作為基礎數(shù)據(jù)而言有重要的意義。

圖4 上海中心城區(qū)的風向變化轉移概率矩陣Fig.4 Transition matrix of wind direction variation in urban area of shanghai

圖5 人工反演的風向變化時間序列Fig.5 Artificially generated minutely time series for wind direction variation

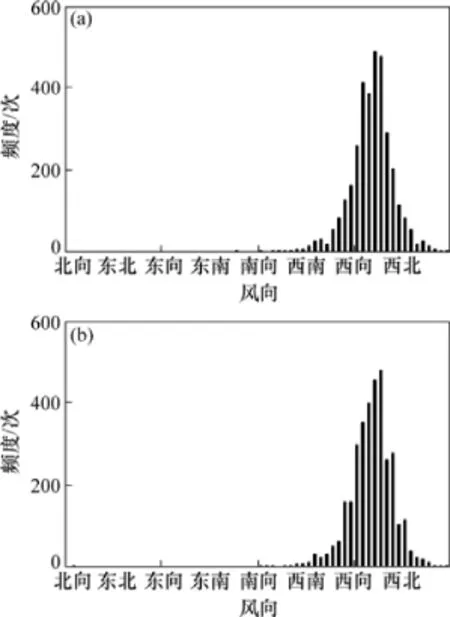
圖6 實測樣本和反演樣本的風向頻度分布直方圖Fig.6 Frequency distribution of measured data and generated data

4 結論

(1)提出基于馬爾可夫過程的基本原理的自然風風向的計算機建模方法，闡釋該方法的有效性和合理性。

(2)基于上述方法和實測數(shù)據(jù)，構建上海地區(qū)的概率轉移矩陣，可為相關研究提供參考。

[1]LI Gong, SHI Jing.Application of Bayesian model averaging in modeling long-term wind speed distributions[J].Renewable Energy, 2010, 35(1): 1192-1202.

[2]張國強, 陽麗娜, 周軍莉, 等.自然通風潛力評估體系的建立與應用[J].湖南大學學報: 自然科學版, 2006, 33(1): 25-28.ZHANG Guo-qiang, YANG Li-na, ZHOU Jun-li, et al.Development and application of natural ventilation potential evaluation system[J].Journal of Hunan University: Natural Science, 2006, 33(1): 25-28.

[3]黃小培, 覃崢嶸, 韋革寧.桂西酸雨的季節(jié)分布及風向頻率統(tǒng)計特征分析[J].氣象研究與應用, 2008, 29(4): 10-13.HUANG Xiao-pei, QIN Zheng-rong, WEI Ge-ning.Seasonal distribution characteristics of acide rain in the west of Guangxi and statistic characteristics of wind direct[J].Journal of Meteorological Research and Application.2008, 29(4): 10-13.

[4]王嘉松, 陳達良, 黃震, 等.實際大氣條件下汽車尾氣擴散的模擬與觀測[J].上海交通大學學報, 2005, 39(11): 1891-1894.WANG Jia-song, CHENG Da-liang, HUANG Zhen, et al.The prediction and field observation for pollutant dispersion fromvehicular exhaust plume in real atmospheric environment[J].Journal of Shanghai Jiaotong University, 2007, 28(12):1335-1338.

[5]芮曉明, 馬志勇, 康傳明.小尺度風特性建模與分析[J].太陽能學報, 2007, 28(12): 1335-1338.RUI Xiao-ming, MA Zhi-yong, KANG Chuan-ming.Modeling and analysis of wind characteristics with little periods[J].Acta Energiae Solaris Sinica, 2007, 28(12): 1335-1338.

[6]曹娜, 趙海翔, 任普春.風電場動態(tài)分析中風速模型的建立及應用[J].中國電機工程學報, 2007, 27(36): 68-71.CAO Na, ZHAO Hai-xiang, REN Pu-chun, et al.Establish and application of wind speed model in wind farm dynamics analysis[J].Proceedings of CSEE, 2007, 27(36): 68-71.

[7]Dunn R W, Li F, Miranda M S.Generation adequacy studies using new spatially correlated wind speed modeling[J].Advances of Power System & Hydroelectric Engineering, 2007,23(11): 45-52.

[8]Sahin A D, Sen Z.First-order Markov chain approach to wind speed modeling[J].Journal of Wind Engineering and Industrial Aerodynamics, 2001, 89(3/4): 263-269.

[9]Kantz H, Holstein D, Ragwitz M, et al.Markov chain model for turbulent wind speed data[J].Physica A: Statistical Mechanics and its Applications, 2004, 342(1/2): 315-321.

[10]Shamshad A, Bawadi M A, Hussin W, et al.First and second order Markov chain models for synthetic generation of wind speed time series[J].Energy, 2005, 30(5): 693-708.

[11]Pourmousavi K S A, Ardehali M M.Very short-term wind speed prediction: A new artificial neural network–Markov chain model[J].Energy Conversion and Management, 2011, 52(1):738-745.

[12]Dobigeon N, Tourneret J.Joint segmentation of wind speed and direction using a hierarchical model[J].Computational Statistics& Data Analysis, 2007, 51(12): 5603-5621.

[13]Carta J A, Ramírez P, Bueno C.A joint probability density function of wind speed and direction for wind energy analysis[J].Energy Conversion and Management, 2008, 49(6): 1309-1320.

[14]劉次華.隨機過程[M].第四版.武漢: 華中科技大學出版社,2008: 26-30.LIU Ci-hua.Stochastic process[M].4th Ed.Wuhan: Huazhong University of Science and Technology Press, 2008: 26-30.