基于X射線脈沖星的 “夸父A”衛星自主導航和軌道控制

趙露華 費保俊 肖 昱 姚國政

裝甲兵工程學院基礎部，北京 100072

?

基于X射線脈沖星的 “夸父A”衛星自主導航和軌道控制

趙露華 費保俊 肖 昱 姚國政

裝甲兵工程學院基礎部，北京 100072

討論X射線脈沖星導航技術應用于 “夸父A”衛星的可行性。在“夸父A”衛星上搭載X射線探測器接收3顆脈沖星的脈沖信號，通過測量信號到達衛星和太陽系質心的時間偏差和頻率漂移6個觀測量, 可以確定衛星的3維位置和3維速度。根據衛星狀態與目標軌道的偏差采用小推力方法可以對衛星進行軌道控制。本文對此進行了數值模擬，并給出了相應的分析。結果表明利用X射線脈沖星導航，在現有的技術下就可以將“夸父A”衛星控制在日地系第一平動點halo軌道的附近。

X射線脈沖星導航；halo軌道；“夸父A”衛星；軌道控制

我國“夸父計劃”的科學目標是觀測日地空間天氣連續變化現象，提高空間天氣災害預報的準確度，服務航天通訊等高科技活動, 預計2015年前后實施。“夸父計劃”由3顆衛星組成，其中的“夸父A”衛星定位于日地系第一平動點的halo軌道[1]。之前，NASA和ESA發射的航天器ISEE，SOHO，ACE等也是定位于此。文獻[2]討論了“夸父A”衛星軌道的設計問題，文獻[3]討論了衛星定點在共線平動點附近的控制問題，但只考慮了初始時刻的入軌誤差，而沒有考慮探測器飛行過程中不確定因素的影響，而實際情況下這些因素是不能被忽略的。為了更好的將衛星定位在暈軌道上，必須較精確地對其進行導航定位。

近年來，國內對衛星自主導航進行了研究，其中X射線脈沖星導航(XNAV)技術是一項新興的空間飛行器自主導航技術。其導航中的濾波方法也被學者們分析研究過[4]，利用脈沖星導航系統能夠獨立的實現星座衛星軌道確定[5]。我們認為，采用XNAV技術為“夸父A”衛星定位和軌道控制將具有相對于其它方法明顯的優越性。這是因為：①日地系第一平動點距地球約為150×104km，光信號在地面和衛星間的單向傳播時間約為5s，使得地面與衛星聯系較為困難。搭載XNAV裝置后可以減輕地面測量和通訊的壓力；②在第1、第2、第3平動點的halo軌道本身不是穩定軌道，需要進行不斷的軌道控制才能保持衛星的正常運行。衛星自身攜帶控軌裝置，采用XNAV后軌道保持更為方便和精確；③在halo軌道上運行的衛星定軌并不需要像地球衛星那樣精確，一般說來，halo軌道衛星的定位精度只需要達到km量級就足夠了，因而光信號的時間測量精度只須要求在μs量級，這是現在的X射線探測和信號處理技術完全能夠達到的。

1 Halo軌道衛星的6維狀態方程

以太陽系質心系(BCRS)為慣性系，太陽-地球系質心在BCRS中的加速度可以忽略，故本文將太陽系質心(BBC)近似取在太陽-地球系質心，以此為原點建立旋轉坐標系(會合坐標系){x1,x2,x3}={x,y,z}，其中x1,x2軸在黃道平面內，x1軸由太陽指向地球，x2軸同地球運動方向，如圖1所示。設旋轉坐標系在BCRS中的角速度為ω=ωe3，太陽(S)、地球(E)的引力常數和矢徑分別為μS、rS和μE、rE。采用無量綱化方法，矢徑為r=(x1,x2,x3)的衛星在平動點周圍的運動方程[6]為

(1)

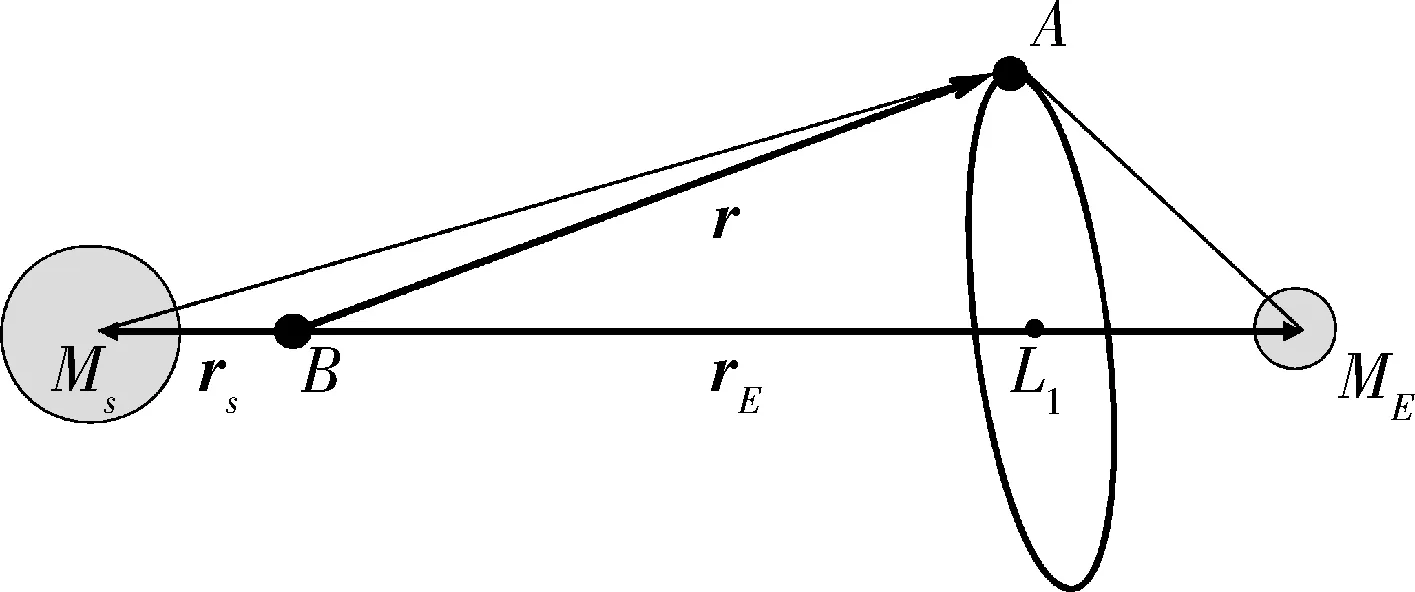
圖1 衛星與太陽、地球的幾何關系

(2)

μ=μE/(μS+μE),μ′=1-μ。根據Legendre函數的生成函數，將牛頓引力勢用Legendre多項式Pn展開并取到第4階(n=2,3,4)，可以求出衛星相對于平動點的周期運動軌跡[7-9]為

(3)

(4)

通常將式(3)稱作平動點周圍的halo軌道，可作為衛星的目標軌道，我們將其記作rh(t)。式中，rL是第一平動點到日地質心距離，振幅A1,A3為設計值(二者滿足一個限制條件)。距離rL、頻率λ、常數k,a21,b21,d21,…等見表1[9]。各項的意義見文獻[7-8]。

對式(1)求變分，得到

(5)

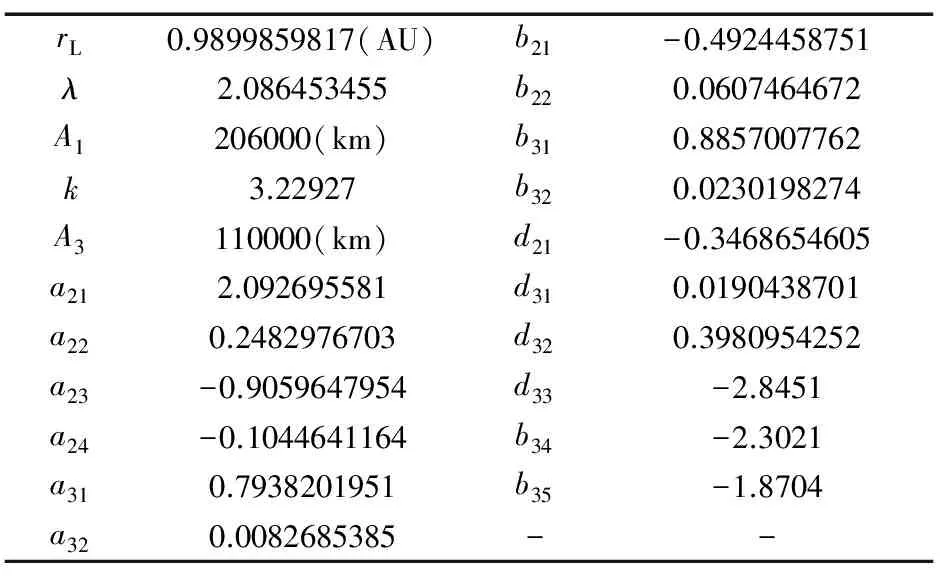
表1 日地系第一平動點halo軌道數據

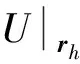
(6)

則式(5)的分量方程可表示為矩陣形式

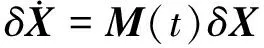
(7)

(8)

將衛星狀態離散化X(t)→X(tk)，時間步長為h=tk+1-tk(k=0,1,2,…)。根據式(7)可得衛星狀態(偏離值)方程

(9)

式中的狀態轉移矩陣Φ與變換矩陣M的關系是

(10)

作線性近似，相當于取分段勻加速運動模型[10]，則有

(11)

2 基于X射線脈沖星的6維觀測方程

假定在衛星上搭載X射線探測器，同時接收3顆脈沖星(p=1,2,3)發射的脈沖，測得3個觀測脈沖輪廓。將脈沖星p的觀測輪廓與SSB接收的相應標準輪廓作比較，得到2個輪廓的時間延遲(包含整波數)和相對頻率偏差為(τp,ζp)，這6個觀測量與衛星的6維狀態量(xi,vi)的關系構成XNAV的6維觀測方程為[10]

(12)

(13)

np和Dp分別是第p顆脈沖星的方向矢量和距離，因▽ρ的量級約為10-8rad，可忽略不計。上面已經完成觀測方程從BCRS到旋轉參考系的轉換，兩式中的r和(v+e3×r)分別是衛星在BCRS中的位置矢量和速度，由于將BCRS原點近似取在日地質心上，r和v又分別是衛星在旋轉參考系的位置矢量和速度，因為定位精度要求不高，不必考慮從BCRS到旋轉參考系的轉換中的相對論效應[11-12]。

定義6維觀測量

(14)

(15)

(16)

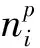
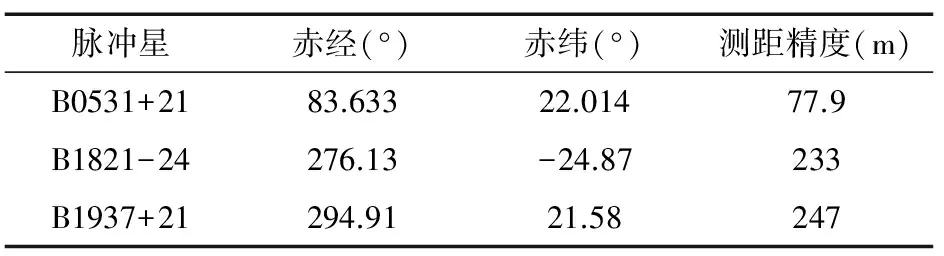
表2 X射線脈沖星坐標和測距精度

3 衛星導航和軌道控制濾波方程

將6維觀測方程(14)與狀態方程式(9)聯立，得到離散系統的濾波方程為：

(17)

矩陣Φ,H由式(11)和(15)給出；Γ,Fk分別是6×6階系數矩陣和6維控制矢量：

(18)

(19)

這里的ai(i=1,2,3)是tk時刻ei方向單位質量推力，由衛星自身軌道控制裝置提供，Δt是施加推力的時間間隔；Vk,Wk分別是6維觀測噪聲和狀態噪聲矢量，其統計特性假定如下：

(20)

(21)

根據式(17)可以一并進行衛星定位和軌道控制。圖2是信號流程框圖，觀測量Z輸入信號處理系統G，在不加控軌處理的情況下(F=0)計算衛星狀態偏差δX。如果偏差在設定值范圍內則直接輸出定位信號；如果偏差大于設定值則反饋到控軌裝置F，再作信號處理后輸出定位信號X。

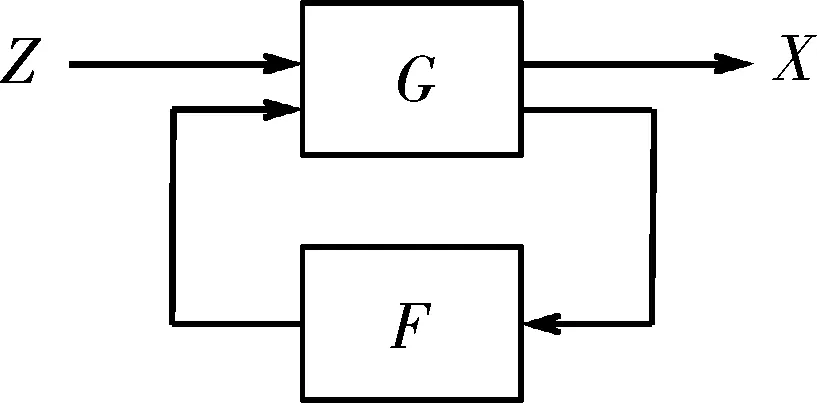
圖2 信號流程圖

4 仿真實驗結果及其分析

采用擴展Kalman濾波方法，仿真條件設為：衛星在t=0時刻入軌，入軌時狀態的偏離值：

δX0=[2×105,2×105,2×105,0.2,0.2,0.2]T。

選取濾波器初值：

初始狀態估計誤差方差矩陣：

P0=diag(5002, 5002, 5002, 0.052, 0.052, 0.052)。

假設過程噪聲為零均值高斯白噪聲，其協方差陣為：

Q=diag(5002, 5002, 5002, 0.052, 0.052, 0.052)。

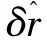
(22)

其中N=diag(k,k,k,1,1,1)。讓K取最小值，即：

(23)

則單位質量推力為：

(24)

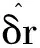
(25)

控制衛星的單位質量所消耗的能量：

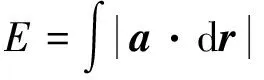
(26)

圖3 控軌后軌道與目標軌道的比較

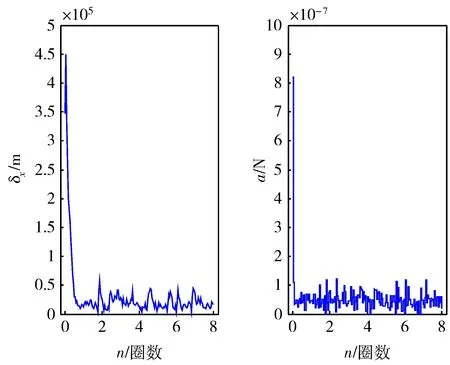
圖4 控軌軌道與目標軌道距離曲線及所需的推力

實驗中將各參數無量綱化后再進行計算。取k=25，觀測8圈，每圈濾波20次。圖3為控制后衛星實際運動軌跡和目標軌道疊加后的效果,2條曲線基本重合在一起。圖4為控制后軌道與目標軌道距離曲線及所需的小推力，濾波器穩定后衛星狀態估計的均方根誤差如表3，衛星運行每一圈速度增量及消耗能量如表4。

表3 濾波器穩定后衛星狀態估計的均方根誤差

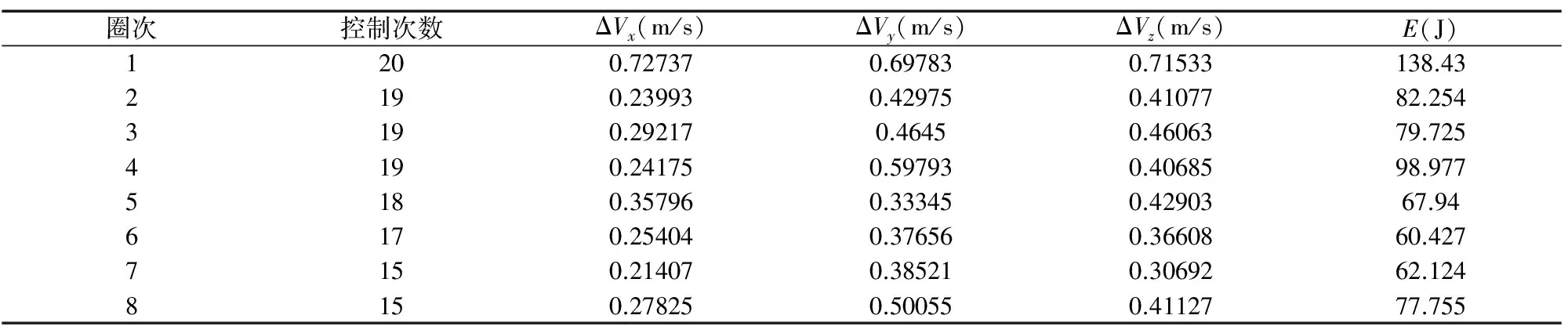
表4 衛星運行每一圈控制的次數、速度增量及單位質量消耗能量

從結果可以看出，考慮衛星初始入軌位置誤差和測量誤差，即使脈沖星導航定位的精度只在km的數量級，利用小推力方案和EKF算法，還是可以將衛星保持在標準軌道附近，且控制次數有減小的趨勢。衛星運行第一圈速度增量較大，能量消耗較多，是因為衛星入軌時與標準軌道偏離較大。除第一圈外，其余各圈，每個方向速度增量均少于1m/s，衛星單位質量消耗能量少于100J。由此可見在現有的技術下，可以將衛星控制在日地系第一平動點附近的halo軌道上。

5 結論與討論

實驗中若取濾波周期Δt較長，則所需能量會減少，但是會導致濾波器誤差較大；而濾波周期Δt太短，則會導致控制的次數太多，能量損失較大。位置控制在總控制中的權重k的選取對結果也有較大影響，k較大時按位置控制的比重大，會使實際軌道相對于標準軌道擺動幅度較大，控制所需能量較大；而k較小時按速度控制的比重大，會使實際軌道相對于標準軌道偏離幅度較大，也不利于軌道控制。關于這兩點文獻[3]和[10]均有提及，本文所選的參數也未必是最理想的。但是本文旨在提供一種 “夸父”衛星自主導航及控軌的方法，說明XNAV可以在“夸父”衛星上應用。

[1] 涂傳詒，Eric Donovan, Rainer Schwenn,等.夸父日地系統與空間天氣探測計劃介紹[C].第11屆全國日地空間物理學術討論會，山東青島，2005,10：4 (TU Chuanyi, Eric Donovan, Rainer Schwenn, et al.The Ntroduction of Braggadocio of the Sun-Earth System and Space Weather Detection Scheme [C]．The 11th Sun-Earth Space Physics Colloquium,Qingdao, Shandong, 2005,10:4.)

[2] 胡少春, 孫承啟, 劉一武．基于不變流形的夸父衛星A軌道設計[J]．航天控制, 2009, 27(3): 37-41.(HU Shaochun，SUN Chengqi,LIU Yiwu.Orbit Design for Satellite Kuafu 2A Based on Invariant Manifolds[J].Aerospace Control, 2009, 27(3): 37-41.)

[3] 侯錫云, 劉林．關于探測器定點在共線平動點附近的控制問題[J]．飛行器測控學報，2005，24(6):29-33． (HOU Xi-yun, LIU Lin.On Orbit Control of Spacecraft around Collinear Libration Points[J].Journal of TT&C Technology,2005,24(6):29-33．)

[4] 要俊杰, 費保俊,許世蒙, 等.X射線脈沖星導航中的濾波方法分析[J].航天控制, 2011, 29(4): 43-48.(YAO Junjie, FEI Baojun, XU Shimeng, et al.The Analysis of Filtering Methods in Navigation Based on X-ray Pulsars[J].Aerospace Control,2011,29(4):43-48.)

[5] 熊凱, 魏春嶺, 劉良棟.基于脈沖星的衛星星座自主導航技術研究[J].宇航學報，2008，29(2): 545-549.(XIONG Kai, WEI Chun-ling, LIU Liang-dong.Research on the Autonomous Navigation of Satellite Constellation Using Pulsars[J].Journal of Astronautics, 2008, 29(2): 545-549.)

[6] Richardson D L.Halo Orbit Formulation for the ISEE-3 Mission[J]. J.Guid.Contr., 1980, 3(6): 543-548.

[7] Richardson D L.A Note on the Lagrangian Formulation for Motion about the Collinear Points[J].Celestial Mechanics and Dynamical Astronomy,1980,22:232-236.

[8] R.Thurman and P.A.Worfolk.The Geometry of Halo Orbits in the Circular Restricted Three Body Problem[D]. Univ.Minnesota, Minneapolis, MN, Tech.Rep.GCG 95, 1996.

[9] Kulkarni J E, Campbell M C , Dullerud G E .Stabilization of Spacecraft Flight in Halo Orbits: an Approach[J].IEEE Control Systems Technology, 2006,14(3): 572-578.

[10] 費保俊，姚國政，杜健，等．X射線脈沖星自主導航的脈沖輪廓和聯合觀測方程[J]．中國科學：物理學 力學 天文學，2010, 40(5)：644-650.(FEI BaoJun, YAO Guozheng, DU Jian,et al.The Pulse Profile and United Measurement Equation in XNAV[J].Scentia Sinica Phys,Mech & Astron，2010, 40(5):644-650.)

[11] 費保俊，孫維瑾，潘高田，等．X射線脈沖星自主導航的光子到達時間轉換[J]．空間科學學報，2010, 30(1)：85-90.(FEI Baojun, SUN Weijin, PAN Gaotian,et al.Transformation of Photon Time of Arrival in XNAV[J].Chinese Journal of Space Science, 2010, 30(1):85-90.)

[12] 費保俊，潘高田，肖昱，等．X射線脈沖星自主導航的衛星運動方程[J]．空間科學學報，2011, 31(2)：304-309.(FEI Baojun, PAN Gaotian, XIAO Yu,et al. Motion Equation of Satellite in XNAV[J].Chinese Journal of Space Science, 2011, 31(2):304-309.)

[13] Sheikh S .The Use of Variable Celestial X-ray Sources for Spacecraft Navigation[D].Doctor Dissertation．Marylan：University of Marylan, 2005.

The Navigation and Orbit Control of Kuafu-A Satellite Based on XNAV

ZHAO Luhua FEI Baojun XIAO Yu YAO Guozheng

Fundamental Department，Academy of Armored Force Engineering，Beijing 100072, China

ThefeasibilityoftheapplicationofX-raypulsar-basedautonomousnavigation(XNAV)forsatelliteKuafu-Aisdiscussedinthispaper.WhenKuafu-AisequippedwithX-raydetectortoreceivesignalsfromthreedifferentpulsars,the3Dpositionand3Dvelocityofthesatellitecanbedeterminedby6observationswhichtake3observationsforTOAdeviationand3observationsforfrequencydrifting.Theorbitscontrolcanbeimplementedbythelow-thruststrategyaccordingtothedeviationofthestatesbetweenthemovingtrackandthetargetorbit.Thenumericalsimulationandthecorrespondinganalysisaregiveninthispaper.TheresultsshowthatthesatelliteKuafu-AcanbekeptaroundtheinteriorSun-Earthlibrationpoint(L1),evenusingtheexistingtechnologyofXNAV.

X-raypulsar-basedautonomousnavigation(XNAV);Haloorbits;Kuafu-Asatellite;Orbitcontrol

2011-09-16

趙露華(1981-)，女，湖南永州人，講師，碩士，主要研究方向為脈沖星導航和軌道控制研究；費保俊(1956-)，男，湖北洪湖人，教授，研究方向為相對論天體物理與天體力學；肖 昱(1961-)，女，山東榮成人，副教授，主要研究方向為脈沖星導航理論及算法研究；姚國政(1971-)，男，山東文登人，講師，主要研究方向為相對論天體物理與廣義相對論。

P228；P145

A

1006-3242(2012)03-0029-05