空天飛行器迭代制導初值生成方法研究

朱建文 劉魯華 湯國建 徐明亮

國防科技大學航天與材料工程學院，長沙 410073

?

空天飛行器迭代制導初值生成方法研究

朱建文 劉魯華 湯國建 徐明亮

國防科技大學航天與材料工程學院，長沙 410073

針對空天飛行器研究助推段牛頓迭代制導初值生成方法。采用牛頓迭代法求解助推段制導參數，推導了迭代制導算法公式。重點分析了影響收斂精度的主要因素，針對迭代初值對其有較大影響的問題，提出了將理論推導與數據插值融合的迭代初值求解算法。仿真結果表明，此算法可以實現空天飛行器助推段迭代初值與制導參數的快速生成，收斂精度滿足設計要求。

空天飛行器；助推段；制導；牛頓迭代；迭代初值

當前，快速、靈活、高精度的確定制導參數是空天飛行器制導技術發展的必然方向。制導問題可認為是一個兩點邊值問題，其解析求解往往是非常困難的，現主要有射表擬合和積分計算2種方法。牛頓迭代制導利用當前狀態與終端要求的偏差，綜合牛頓迭代算法的基本思想，實時確定制導參數，以此制導參數來擬定制導指令。這種制導方法具有算法簡單，易于彈上實現等優點。目前牛頓迭代制導方法已有成功應用的先例，例如美國發射小衛星的Pegasus火箭就采用牛頓迭代制導法。

文獻[1]研究了傳統的迭代制導算法，文獻[2]介紹了牛頓迭代法在載人飛船上升段彈道設計的應用；文獻[3]對固體運載火箭上升段彈道快速設計方法做了研究，對迭代初值，采取三維插值的方法，此方法計算量大且生成速度較慢；文獻[4～7]研究了牛頓迭代制導在固體小火箭及彈道導彈中的應用，但沒有對迭代初值的生成做深入研究。本文基于彈道積分計算，研究牛頓迭代法在空天飛行器助推段制導參數快速生成中的應用，分析了影響迭代精度與速度的主要因素。為解決牛頓迭代法對初值敏感的問題，文中針對不同的初值分別采取了理論推導與二維數據插值的方法。

1 牛頓迭代算法原理

牛頓迭代法是一種依據對非線性方程組逐次線性化的思想建立起來的迭代法。其基本原理如下，設x∈D為非線性方程組

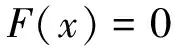
(1)

的解，x(k)∈D是近似解。若F(x)在x(k)附近可微，則在x(k)附近可將F(x)線性化為

(2)

因此，在x(k)附近方程組近似地簡化成線性方程組

(3)

當F′(x(k))非奇異時，線性方程組(3)存在唯一解，記其為x(k+1)，可得到

(4)

2 迭代計算制導參數

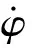
(5)

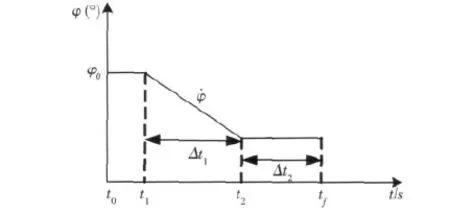
圖1 飛行程序角模型

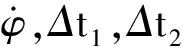
(6)

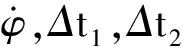
(7)

3個未知數3個約束方程，可以利用牛頓迭代算法進行迭代計算。這里首先進行線性微分，在h0，v0，θ0處線性展開得到：

(8)

其中：

(9)

根據文獻[3]，有以下關系：

(10)

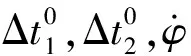
(11)

取終端高度、速度及速度傾角精度要求分別為ε1,ε2和ε3，誤差量分別為Δh,Δv和Δθ。可以得出牛頓迭代計算制導參數的流程如圖 2所示:

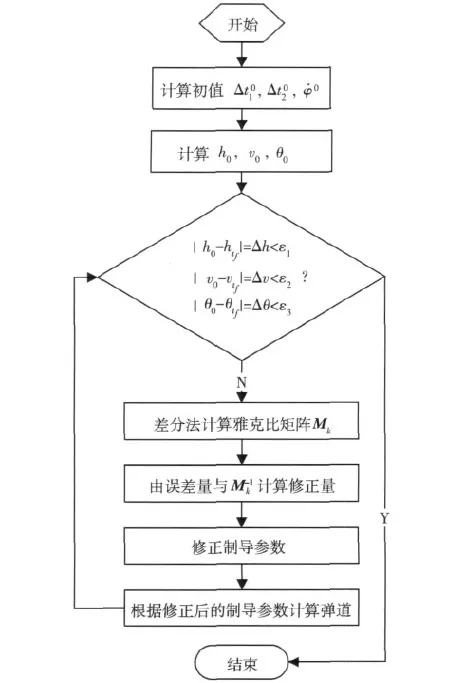
圖2 程序角參數迭代流程

在牛頓迭代法計算中關鍵是求雅克比矩陣，直接用求偏導數的方法來求矩陣每一個元素使得該方法依賴于對變量數值的選取。由于沒有具體的解析表達式，只能采用數值解法，因此牛頓迭代法的收斂性與初始值的選取、變量維數以及計算雅克比矩陣中選取的增量有關。根據文獻[3]，收斂精度主要受迭代初值的影響。

3 計算迭代初值

3.1 計算時間初值

(12)

其中vg為由攻角和引力引起的速度損失，vtf為終端速度要求，v0為當前速度。

(13)

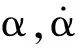
(14)

其中atf=P/mtf為火箭在tf時刻的推力加速度。實際的速度增量為：

(15)

這里記T=tf-t1，中間變量

(16)

令

(17)

則

(18)

求導得出

(19)

同時

(20)

其中a為推力加速度。則

(21)

故

(22)

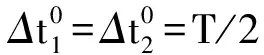
3.2 計算俯仰角變化率

4 算例分析

取牛頓迭代起始時刻的狀態為：v=4157.40m/s，h=78166m，θ=4.75°。終端狀態約束為vtf=4417m/s，htf=88848m，θtf=1.5°，制導周期取0.5s，計算步長取0.02s，制導起始時刻為168s，終止時刻為191s，高度精度為10m，速度精度為1m/s，速度傾角精度為0.1°。

從表 1中可以看出在牛頓迭代制導中初值的不同會導致計算結果的較大偏差，在對初值進行計算校正后，計算精度均提高一個數量級。從圖 3中可以看出，初值修正后，俯仰角比標準程序有較大調整，原因是在每一個制導周期內，通過計算都需對制導參數進行調整。

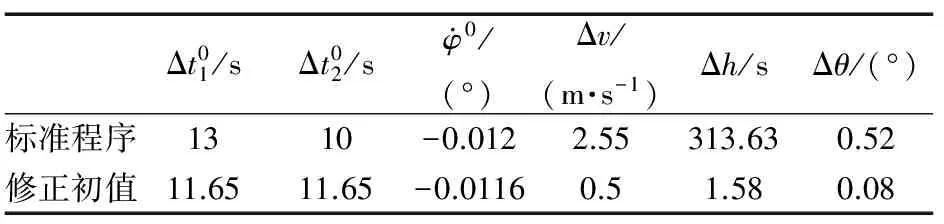
表1 2種初值計算結果對比

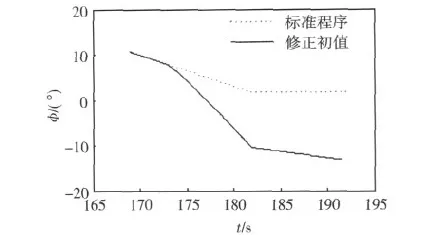
圖3 俯仰角-時間變化曲線

5 結論

研究了空天飛行器助推段牛頓迭代制導方法。從牛頓迭代算法出發，介紹了其制導實現的基本過程，另外分析了影響迭代精度的主要因素。針對牛頓迭代法對初值敏感問題，在計算迭代初值的過程中，采取將插值法與解析法相結合的方法，分別對不同迭代初值的選取進行了研究。通過仿真計算證明，此迭代初值的選取可以有效提高迭代制導的精度，并且只需進行二維插值計算，此方法可以提高初值的生成速度，另外也可以提高制導精度。

[1] 李華濱，李伶．小型固體運載火箭迭代制導方法研究[J]．航天控制，2002，2：29-37.(Li Huabin,Li Ling.Iterative Explicit Guidance for Small Solid Launch Vehicle[J].Aerospace Control，2002，2：29-37.)

[2] 陳克俊．載人飛船上升段軌道的Newton迭代設計法[J]．國防科技大學學報，1992，14(2)：66-71.(Chen Ke-jun．Newton iterative Design Approach for Manned Spacecraft Ascent Traje- ctory[J]．Journal of National University of Defense Technology，1992，14(2)：66-71.)

[3] 楊希祥，江振宇，張為華.固體運載火箭上升段彈道快速設計方法研究[J].宇航學報，2010，4(4): 993-996．(Yang Xixiang,Jiang Zhenyu,Zhang Weihua.Rapid Design Method for Ascent Trajectory of Solid Launch Vehicles[J].Journal of Astronautics, 2010，4(4): 993-996.)

[4] 劉新建，袁天寶.固體小運載的制導方案設計與仿真[J].系統仿真學報，2005，11(17):2734-2736.(Liu Xinjian, Yuan Tianbao.Guidance Design and Simu- lation for Launching Satellite with Solid Rocket[J].Journal of System Simulation,2005,11(17):2734-2736.)

[5] T Shima, M Idan.Sliding-Mode Control for Integrated Missile Autopilot Guidance[J].Journal of Guidance, Control, and Dynamics,2006:16-19.

[6] Daniel Rovner.GN&C for Pegasus Air-launched Space Booster : Design and First Flight Result[R].NASA,991105.

[7] Kang Jianbin, Zhao Jianting.An Anti-interference Guidance Scheme for Ballistic Missile[R].AIAA 2005-3268.

Research on Initial Values of Newton Iterative Guidance for Aerospace Vehicles

ZHU Jianwen LIU Luhua TANG Guojian XU Mingliang

College of Aerospace and Material Engineering，NUDT, Changsha 410073, China

TheNewtoniterativemethodforboostphraseofaerospacevehiclesisresearched.Thismethodisusedtoobtainguidanceparametersanddeducetheiterativeformula．Meanwhile，byconsideringthattheNewtoniterativemethodissensitivetotheinitialvalueofparameters，thegeneratedmethodsisintroducedforinitialvaluesonthebasisofdatainterpolationanddeducing.Thesimulationresultsshowthatitisfeasibletoobtainguidanceparametersforaerospacevehiclerapidlywiththealgorithmproposedinthepaper.

Aerospacevehicles；Boostphrase；Guidance；Newtoniterative;Initialvaluesofguidance

2011-12-06

朱建文(1987-)，男，甘肅定西人，碩士研究生，主要研究方向為飛行器動力學、制導與控制；劉魯華(1977-)，男，西安人，講師，主要研究方向為飛行器動力學、制導與控制；湯國建(1964-)，男，江蘇金壇人，教授，博士生導師，主要研究方向為飛行器動力學、制導與控制；徐明亮(1982-)，男，河北盧龍人，博士研究生，主要研究方向為飛行器動力學、制導與控制。

V448.231

A

1006-3242(2012)03-0061-04