關于緊支集多元小波的一種算法

胡 愛，邸繼征

（浙江工業大學 理學院，浙江 杭州 310023）

關于緊支集多元小波的一種算法

胡 愛，邸繼征

（浙江工業大學 理學院，浙江 杭州 310023）

在小波分析的實際應用中，多元小波對分解和重構圖形圖像等是很有用的，然而小波系數的計算是一個困難問題.眾所周知，小波系數是由所考查的函數與小波基函數乘積的積分定義的.由于函數往往只由抽樣值給出，所以前述積分需要用近似計算的方法得到，如果大量小波系數都通過這種方法計算，必將帶來巨大的工作量，而如果把一元小波Mallat算法的思想推廣到多元的情形就可以得出緊支集多元小波系數的計算方法，即相應于這類小波的Mallat分解和重構算法.在一個積分極限定理的基礎上，由函數抽樣值得到了近似計算這些系數的公式.通過這些公式可以直接由函數抽樣值算出小波系數，得到抽樣值算法.

多元小波；分解；重構；Mallat算法；抽樣值

在圖像處理中平面圖像和立體圖像都需要用多元函數來描述，尤其是二維平面圖像是基本組成部分，所以多元小波在分析圖像材料等方面顯得尤為重要，然而計算小波系數不是一件容易的事情.一元情形的分解和重構已經討論過［1］，將一元Mallat算法的思想推廣到多元的情形，給出了多元Mallat算法的分解和重構公式.正如一元小波的情況，對一些函數f，我們需要知道“幾個系數”，其他的就可以通過公式計算出來.而f常常是不知道的，所以連幾個系數也很難獲得，因此對大多數小波來說沒有明確的表述，而Mallat算法還是難免積分，所以計算起來相當困難.在實際問題中，基本上都是通過函數在抽樣點處的值對其進行了解的，因此函數抽樣值［1］近似計算緊支集多元小波系數［2］的方法對解決上述難題也是很有效的.

1 基本結論、符號和概念

令｛Vj｝j∈z為L2（R）上對于尺度函數φ 的一個多分辨分析，相應的小波ψ滿足

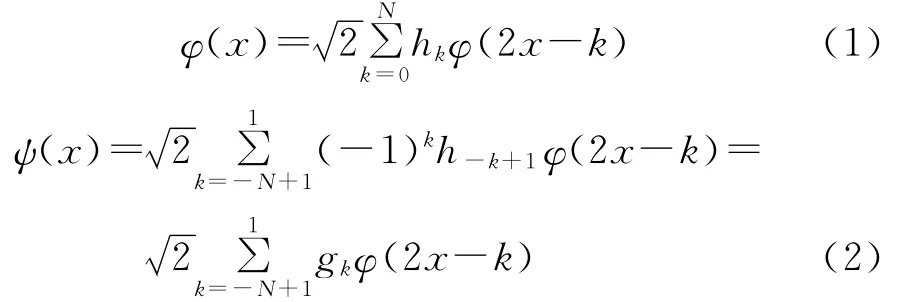
其中：Z為整數集；R＝（－∞，∞）hk為實數；N＝2K－1，K 為正整數，gk＝（－1）kh－k＋1.

令V2j＝Vj?Vj，那么｛V2j｝j∈z是L2（R2）上的一個多分辨分析［3］.因為

2 多元小波的Mallat算法

考慮到圖像處理中二維圖像是基本組成部分，因此下面以二元小波的Mallat算法為例說明其分解與重構過程.

與一元情形一樣，根據函數f的實際情況，大致選取一個整數j，記該函數為f＝fj∈V2j.比如，若

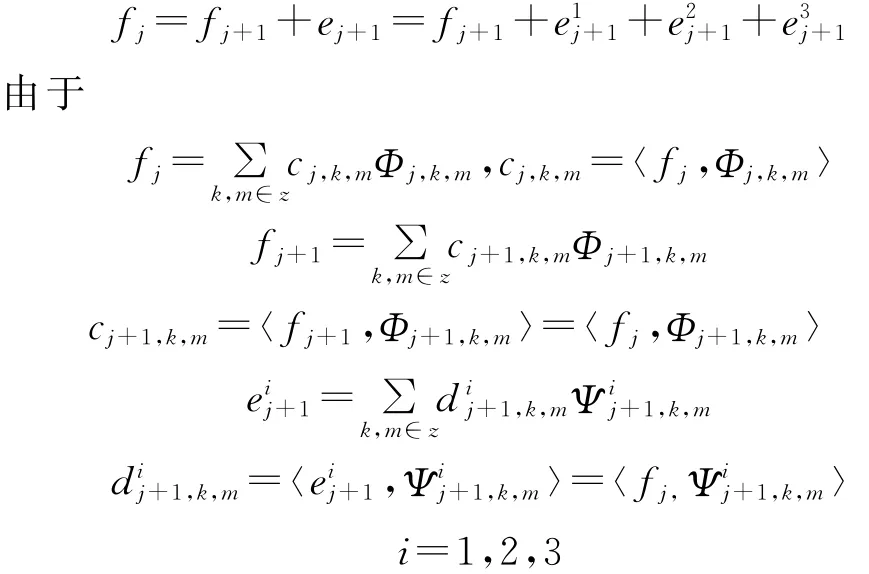
因此在上述二元情形下，對hi為實數，且hi＝0，i?Z0，N，其 中 Z0，N＝ ｛0，1，…，N－1，N｝，N＝2 K－1，K為正整數，尺度函數是由式（1）定義，小波是由式（2）定義的緊支集函數時，有如下分解定理.

定理1

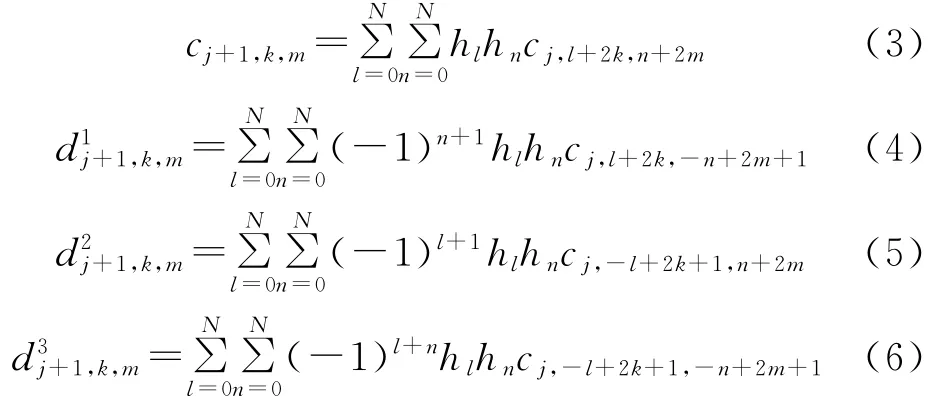
式（3－6）構成二元情形的Mallat分解算法，下列定理給出相應的重構公式.

定理2 當k＝2p－1，m＝2q－1，p，q為整數

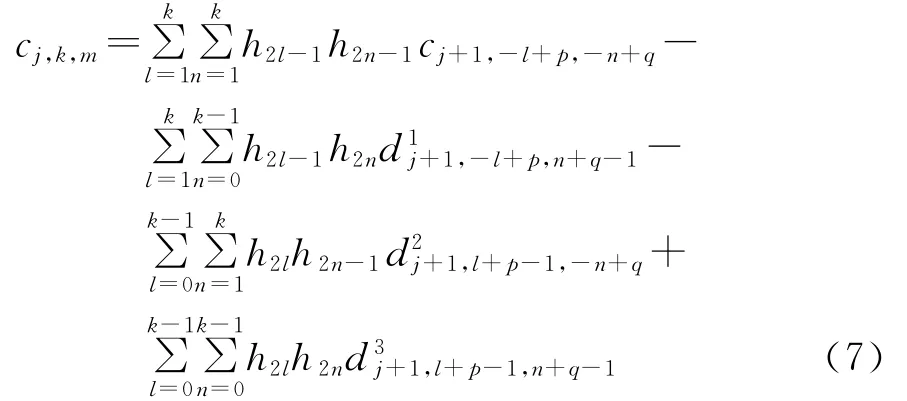
3 抽樣值算法

與一元情形一樣，Mallat算法是在假定一些系數已知的前提下求另一些系數，不能免除積分.如果能夠用函數在一些點的值直接計算出系數，必會為Mallat算法的應用帶來極大的方便.

以下討論這個問題，并在尺度方程為式（1），小波表示為式（2）的條件下進行.

首先介紹兩個記號.記

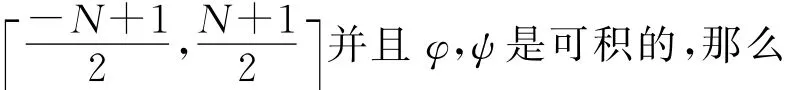
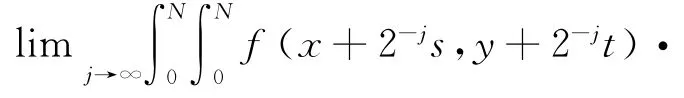
由以上定理，并令f－j∈V2－j，可得定理4.

定理4 當j＞0足夠大時，f－j在（2－jk，2－jm）附近連續時，

利用式（19，20），如果用－j或－j＋1分別取代式（3—10）的j或j＋1，我們就能得出分解和重構公式.

4 結 論

通過將一元小波的Mallat算法推廣到多元的情形，構造出了緊支集多元小波的Mallat算法，并給出了具體計算小波系數的分解和重構公式.在很大程度上已經克服了原來所有系數都通過抽樣值計算的高復雜性和誤差大的缺點.在Mallat分解和重構公式里也需要先知道一些系數的值.對此，用函數在一些點的抽樣值先直接計算出部分系數的方法又免除了一些積分的計算，這不僅大大降低了Mallat算法近似計算積分的冗余度，也為它的應用帶來了很大的方便.

［1］成禮智，王紅霞，羅永.小波的理論與應用［M］.北京：科學出版社，2004.

［2］DI Ji-zheng.Construction of a kind of wavelets［J］.Journal of Mathematical Research and Exposition，2001，21（4）：495-499.

［3］DAUBECHIES I.小波十講［M］.李建平，譯.北京：國防工業出版社，2004.

［4］陳仲英，巫斌.小波分析［M］.北京：科學出版社，2007.

［5］徐利治.函數逼近的理論與方法［M］.上海：上海科學技術出版社，1983.

An algorithm for compactly supported multivariate wavelets

HU Ai，DI Ji-zheng
（Collage of Science，Zhejiang University of Technology，Hangzhou 310023，China）

In the practical application of wavelet analysis，multivariate wavelet is useful for decomposition and reconstruction of graphs and images.However，it is quite difficult to calculate the wavelet coefficients.It may be well-known that wavelet coefficient is defined by integral of the product of the discussed functions and the wavelet basis functions.Since the function is often given by the sample values，the integral mentioned above need to be calculated approximately.If a large number of wavelet coefficients are calculated in this way，it will be a heavy workload.If the idea of Mallat algorithm of univariate wavelet is applied to multivariate wavelet，we can deduce Mallat algorithm of compactly supported multivariate wavelet.Based on an integral limit theorem，an approximate formula is obtained for the calculation of coefficients by sampling values.With the help of these formulas，we can get the wavelet coefficients directly by sampling value of function.

multivariate wavelets；decomposition；reconstruction；Mallat algorithm；sample value

OS1.86

A

1006-4303（2012）01-0115-04

2010-10-22

胡 愛（1984—）女，山西朔州人，碩士研究生，主要從事小波分析應用研究，E-mail：huaixin.xin＠163.com.通信作者：邸繼征教授，E-mail：dijiz＠zjut.edu.cn.

（

劉 巖）