均勻帶電細圓環電場的計算機模擬

尹妍妍 梁志強 劉進慶 辛志榮

（山東交通學院理學院，山東 濟南 250023）

均勻帶電細圓環電場的計算機模擬

尹妍妍 梁志強 劉進慶 辛志榮

（山東交通學院理學院，山東 濟南 250023）

用Matlab程序對均勻帶電細圓環在空間激發的電場進行了計算機模擬，可以輸出帶電圓環附近任意一點的電場強度及電勢，做出了過環心與圓環垂直的平面內的等勢線，以及三維空間的等勢面，實現了電場的可視化，便于形象地理解帶電圓環激發電場的空間分布.

均勻帶電細圓環；計算機模擬；Matlab；等勢面；可視化

1 引言

靜電場的研究在大學物理教學中起著重要的作用，是研究電磁學的基礎.均勻帶電細圓環電場的研究就是一個非常典型的例子.近年來關于均勻帶電細圓環電場的討論很多；文獻［1］在直角坐標系中導出電勢和電場強度的級數解；文獻［2］、［3］把電場強度表示為橢圓積分；文獻［4］在柱坐標系中得到電場的級數解，但是這些方法計算比較冗長且結果多以數學表達式的形式給出，不利于工科學生理解電場的分布；文獻［5］雖然采用了數值計算的方法計算橢圓積分并求出了圓環所在平面的電場強度和電勢，但并不能全面地表示均勻帶電細圓環在空間所產生的電場情況.本文利用Matlab程序用計算機模擬的方法對均勻帶電細圓環在空間激發的電場進行了描述，可以輸出帶電圓環附近任意一點的電場強度及電勢，并做出了過環心與圓環垂直的平面內的等勢線，以及三維空間的等勢面，實現了電場的可視化，為形象地理解靜電場的空間分布提供了幫助.

2 環形帶電體模型

有一半徑為a的細圓環，均勻帶電，帶電量為q，在大學物理課程教材中一般讓學生計算過環心O與環垂直的軸線上的電場強度與電勢［6］.本文則以Matlab程序為基礎對圓環在其附近所激發的電場進行了研究.

3 Matlab模擬計算帶電體激發電場的電勢和電場強度

建立如圖1所示的坐標系，圓環在xOz平面內，在B點處的電荷元dL所帶電量為dq，到達A點的距離為R，在空間A點產生的電勢為

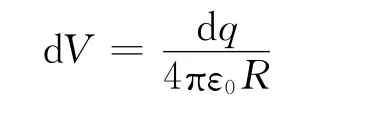
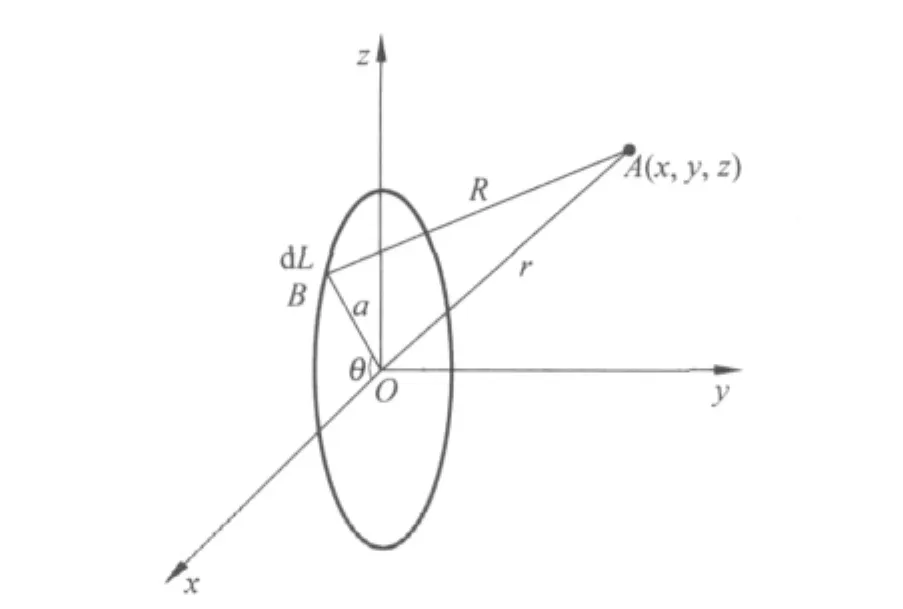
圖 1

計算出空間任一點的電勢后根據電場強度與電勢的關系E＝－ΔV，可以得到空間任意點的電場強度.為了便于計算，我們不妨令圓環帶電量q＝4πε0，圓環半徑a＝1，在可以基本體現電場分布的前提下我們只計算x?（－2，2），y?（－2，2），z?（－2，2）范圍內的電場分布情況.計算過程中我們把圓環均勻地分為40份，每份對應的圓心角為，先計算出每份在數據網格點上產生的電勢dV，然后用數值積分的指令（trapz）計算出整個圓環在數據網格點上產生的電勢.再用Matlab求梯度的指令（gradient）求出E＝－ΔV，近而得到了x?（－2，2），y?（－2，2），z?（－2，2）范圍內數據網格點上的電勢及電場強度（見附錄程序一）.

4 實現電場的可視化

為了更加形象地描述帶電細圓環在空間激發的電場我們還可以用圖像把電場表示出來.

4.1 過環心與環垂直的軸線上的電場

計算出x?（－2，2），y?（－2，2），z?（－2，2）范圍內數據網格點上的電場強度和電勢后，我們可以取出過環心與環所在平面垂直的軸線（即Oy軸）上點的電場強度和電勢的值，把電場強度和電勢隨y軸變化的情況作出圖像.在Oy軸上電場的解析式根據電場的對稱性分析很容易得到，E＝，顯然也可以根據這一解析式作出電場強度和電勢隨y軸變化的情況，我們把兩種方法作出的圖像相比較，如圖2所示，圖中實線表示的是理論數據，“＊”表示的是模擬計算得到的數據，通過圖像可見契合得非常好.

4.2 過環心與環垂直的平面內電勢的分布

利用Matlab程序計算出空間的電勢分布后我們可以調用計算數據，根據這些數據應用Matlab中作二維場線的指令（contour）作出某一個平面內的等勢線.本文以Oxy平面為例作出了該平面的等勢線，如圖3、圖4所示（圖3、圖4是不同視角下Oxy平面的等勢線）

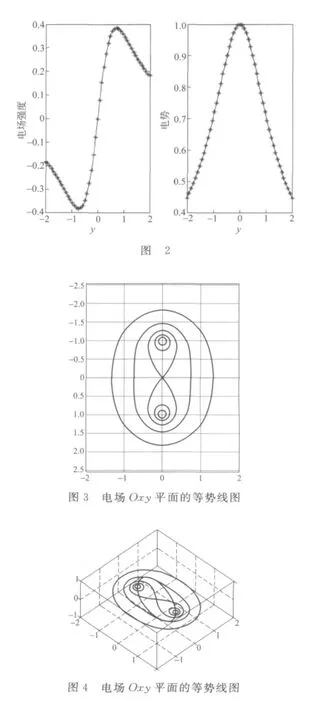
通過圖像可以看到在Oxy平面內等勢線關于Ox軸和Oy軸都呈現出對稱性，這與帶電體關于Ox軸和Oy軸對稱有關，因此可以推測出帶電體的對稱性決定了它所激發電場的對稱性，為學生理解用高斯定理求解具有對稱分布的帶電體的電場打下基礎.另外，Oxy平面是一個過環心與圓環垂直的平面，由圓環的對稱性可知，所有過環心與圓環垂直的平面都具有相同的性質，如果我們知道了其中一個面等勢線的分布情況，不難想象將該面的等勢線沿與圓環垂直的軸（Oy軸）旋轉360°即是該圓環在空間激發電場的等勢面了，所以研究這樣一個面的等勢線對研究整個空間電場分布非常有意義.

4.3 三維空間的等勢面

在計算得到空間各點電勢值的前提下還可以應用Matlab做三維標量場的指令作出均勻帶電細圓環在空間產生的等勢面.本文中我們通過使用patch和isosurface語句來實現.為了更直觀我們采用不同的顏色繪制與圖3中Oxy平面中等勢線對應的5個等勢面如圖5所示，為使圖像更加形象直觀將z軸上半軸的數據清零，得到帶電圓環電場的三維等勢面的截面圖如圖6所示.

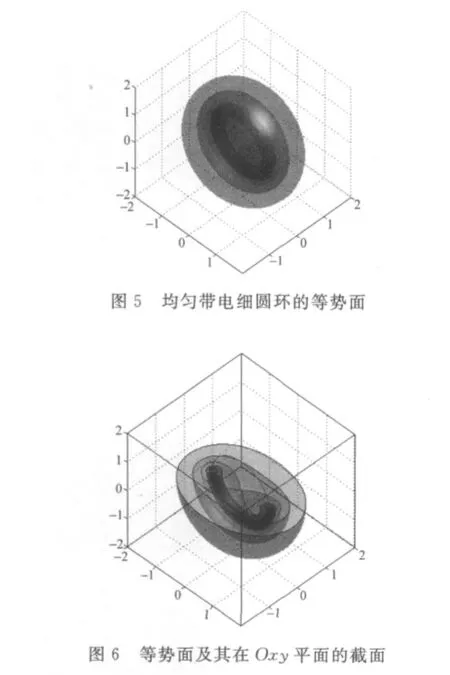
4.4 顯示空間任意點的電場強度和電勢

根據Matlab數據儲存的特點，我們可以用指令調用程序運行結果中的任意一個數據.因此，我們只需要輸入空間某點的坐標即可在屏幕上顯示出該點的電場強度和電勢.但要注意如果輸入的坐標不是數據網格上的點則就近取值進行計算！

運行程序（見附錄程序二），并輸入某點的坐標（注意：該點應該在數據網格點范圍內）運行結果如下：

要求空間一點（0，1，0）的電場強度和電勢，計算機模擬計算給出的是（0，1.04，0）點的電場強度和電勢，結果為V＝0.69311，E＝5.6628e－009＊i＋0.34607＊j＋0＊k，電場強度的大小為E＝0.346 07，而 點 （0，1.04，0）處 理 論 值 為 V ＝0.6931，E＝0＊i＋0.3463＊j＋0＊k，電場強度的大小為E＝0.3463，兩種計算方法有很小的誤差，這是由于數值計算過程中步長的選取以及誤差累積形成的.

5 結論

本文用計算機模擬的方法較詳細地研究了均勻帶電細圓環的電場分布情況，所得出的結論與解析計算進行了比較，在誤差允許的范圍內結果符合得很好.軸線上電場強度、電勢分布圖以及Oxy平面等勢線、三維等勢面進一步加深了學生對環形帶電體在空間激發的電場的認識，對學生學習靜電場有著積極的作用.

附計算程序

程序一：計算x?（－2，2），y?（－2，2），z?（－2，2）范圍內電勢及電場強度.

［1］ 程昌林，王慧，李業鳳.均勻帶電細圓環的電場［J］.大學物理，2003，22（6）：15～17

［2］ 周海英.均勻帶電細圓環的電場的一般分布［J］.大學物理，2004，23（9）：32～34

［3］ 張之翔.圓環電荷的電勢的幾種算法及討論［J］.大學物理，2006，25（8）：7～10

［4］ 劉誠杰.劉景世.均勻帶電細圓環電場的分布［J］.大學物理，2005，（08）

［5］ 曹玉娟.數值積分求解均勻帶電細圓環平面上的電場分布［J］.物理與工程，2005，15（15）：12～14

［6］ 馬文蔚等.物理學（第五版）［M］.北京：高等教育出版社，2006

［7］ 彭芳麟.計算物理基礎［M］.北京：高等教育出版社，2010

2012-01-17）

山東省教育科學“十二五”規劃課題“分層次教學與大學生科學素質及創新能力培養的實踐與研究”，課題編號：2011GG106.