用多分量感應資料快速重建層狀地層的縱橫向電阻率和水平界面深度

汪宏年，商慶龍，朱天竹，李舟波

1.吉林大學物理學院，長春 130012 2.吉林大學地球探測科學與技術學院，長春 130026

用多分量感應資料快速重建層狀地層的縱橫向電阻率和水平界面深度

汪宏年1，商慶龍1，朱天竹1，李舟波2

1.吉林大學物理學院，長春 130012 2.吉林大學地球探測科學與技術學院，長春 130026

研究建立用多分量感應測井資料同時快速重建水平層狀橫向同性介質中橫向與縱向電阻率和層界面深度的有效方法。首先，利用電磁場攝動方程、電導率函數與模型參數關系方程以及模式匹配算法得到電磁場并矢Green函數的半解析解，建立多分量感應測井響應的Frèchet導數矩陣的快速算法；在此基礎上，借助于規范化處理和奇異值分解技術，給出同時反演水平層狀地層中各個地層的縱、橫向電阻率以及層界面深度的迭代過程，實現理論合成資料與輸入資料的最佳擬合。數值計算證明，該反演算法能夠取得較滿意的反演效果。

感應測井；Frèchet導數矩陣快速算法；各向異性地層電阻率和層界面的同時反演

0 引言

多分量感應測井作為能夠同時測量地層縱橫向電阻率的一種新測井技術，在薄交互層、裂縫等各向異性地層評價中發揮著重要作用［1］。與各種常規測井儀器不同，多分量感應測井儀器增加了與井軸方向完全垂直的發射和接收線圈系（共面線圈系），其測量信號能夠提供地層縱向電阻率信息；但由于多分量感應測井儀器產生的相應的感應電磁場空間分布不再具有軸對稱性，且電場方向與地層界面也不再平行，這樣會在地層界面上產生積累面電荷而導致共面線圈系的測井響應更加復雜［2－7］①張燁，汪宏年，陶宏根，等.基于耦合標勢與矢勢的有限體積法模擬非均勻各向異性地層中多分量感應測井三維響應.地球物理學報，待刊.。數值計算結果顯示，共面線圈系的測量結果受井眼和層界面的影響均很大，特別在薄層上或層界面附近往往出現負響應。根據共面線圈系的視電導率σa，xx和σa，yy的大小無法直接估計出地層縱向電阻率的真實變化情況，必須建立一套有效的數據處理技術，以便從測量結果中提取出地層電阻率和層界面。根據筆者目前掌握的資料，多分量感應資料的處理方法主要有2種：一種是Michael等［1］提出的最小二乘法提取縱橫向電阻率方法，該方法直接利用均勻介質中電磁場的解析表達式提取地層電阻率參數，由于沒有考慮層界面影響，其處理結果只是消除了地層的趨膚效應，在地層厚度較小的交互層上或層界面附近將難以取得滿意效果；另一種方法是Zhang等［8］借助迭代反演同時提取層界面和地層電阻率的算法，該算法中沒有建立計算目標函數下降方向的快速有效方法，所以其效率往往很低。對于層狀地層來說，如果不考慮井眼影響，多分量感應數值模擬仍然屬于2.5維問題［2，4］，通過Fourier變化方法可將其轉化成3個軸對稱向量場的求解問題，借助模式匹配方法可以實現快速正演計算。如果將這種快速數值模擬技術與攝動理論結合起來，建立一套有效的Frèchet導數的快速算法［9－10］，就能夠實現多分量感應資料的快速迭代反演。

筆者將研究并建立這種用微分方程反演理論建立起來的多分量感應資料的快速反演方法，將包括攝動方程與Frèchet導數矩陣的快速計算，以及縱橫向電阻率和層界面的迭代反演等內容，最后通過數值模擬結果檢驗在水平層狀垂直井眼中的反演結果。

1 理論

為簡單起見，用圖1表示水平層狀各向異性地層。地層由N＋1個各向異性地層組成，dn（n＝2，3，…，N）表示地層界面深度，每個地層的電導率珔σn＝diag（σhn，σhn，σvn）是對角張量，n＝1，2，…，N＋1其中σhn和σvn分別表示地層橫向和縱向電導率。對于這種層狀地層模型，其電導率空間分布完全由模型向量x＝（σh1，σh2，…，σhn，σv1，σv2，…，σvn，d2，d3，…，dn）確定。建立如圖1所示的坐標系xyz，z軸與地層層面垂直，x軸和y軸與地層層面平行。Mp，p＝x，y，z分別是x，y，z正交磁偶極子產生的磁偶極矩，Rp，p＝x，y，z，分別是x，y，z3個不同方向正交接收線圈位置，如圖1所示，兩者的源距假定為L。p方向的磁偶極子Mp產生的電場Ep和磁場Hp完全由Maxwell方程確定［2－3］：

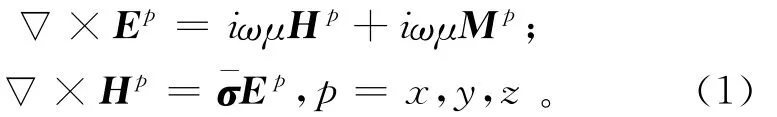
其中：Mp＝＾epMpδ（r－rs），＾ep為坐標p上的單位向量；r和rs分別為場點和源點位置。磁導率μ（H／m）為常數；ω（rad／s）為發射信號角頻率；因發射頻率較低故忽略位移電流影響。

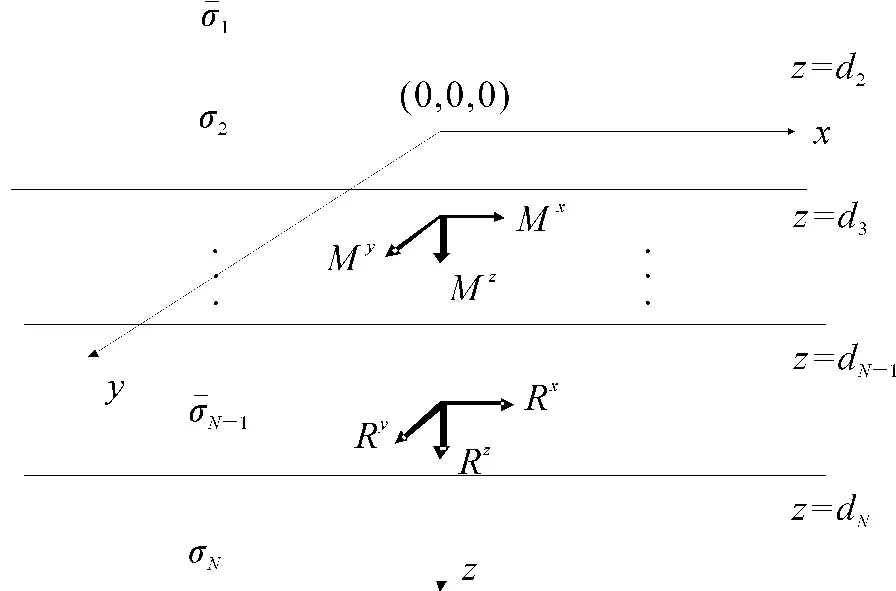
圖1 地層模型與坐標系Fig.1 Formation model and coordinate system

1.1 攝動方程與Frèchet導數矩陣的快速計算

利用攝動理論，從方程（1）中可直接推導出電導率微小攝動δ珔σ與電磁場變化關系：

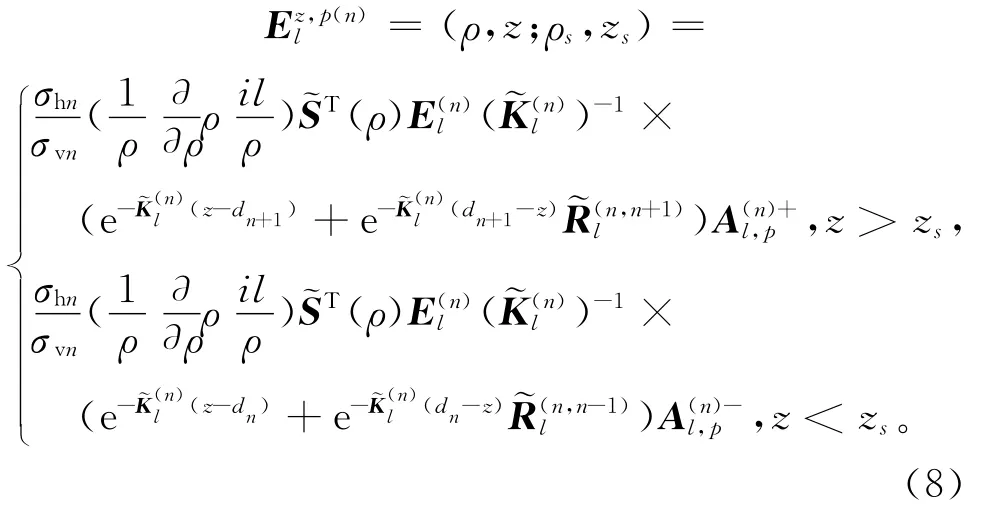
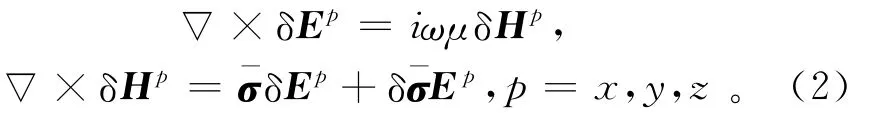
引入磁流源電場并矢Green函數GME（r，rR），磁流源磁場并矢Green函數GMH（r，rR）：

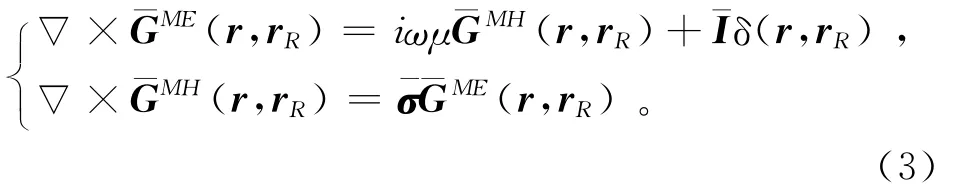
則利用文獻［10－11］中的結果，從方程（2）和（3）中可以得到磁場變化δHp的積分解：

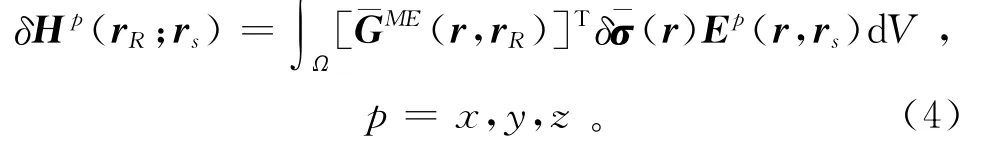
其中：rR是接收點位置；上角標“T”表示轉置。

對于圖1所示的水平層狀地層，電導率是分片常數函數，電導率與模型向量x的各個分量間滿足如下方程［12］：

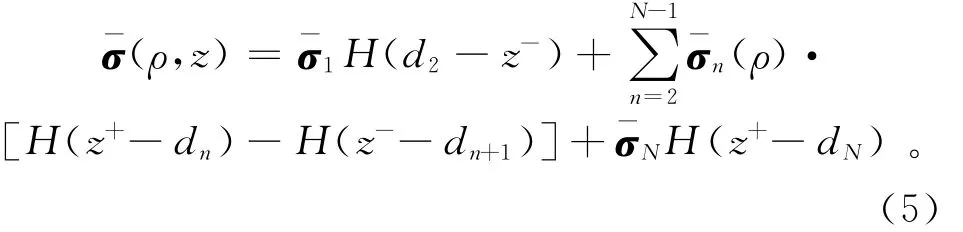
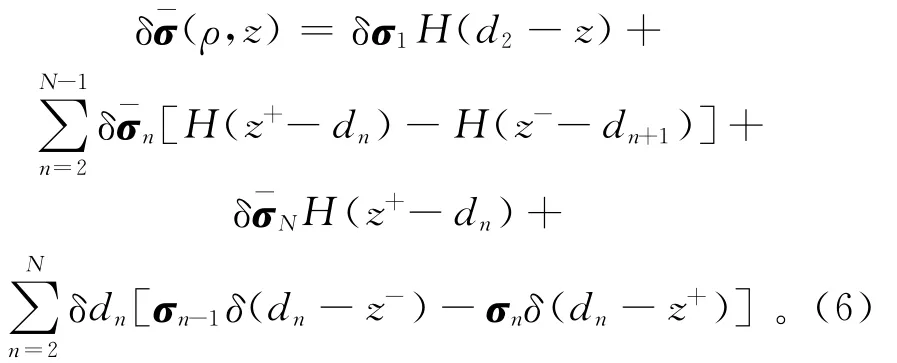
其中：δ珔σn＝diag（δσhn，δσhn，δσvn）和δdn分別表示n層上電導率向量和層界面n的微小變化；δ（z）＝H′（z）是Dirac’sδ函數。

因為發射源位于井軸上，利用模式匹配算法［2－3］，在進行磁場正演計算的同時可得到p方向的發射線圈在地層n上的水平和垂直電場強度各個分量的半解析解：

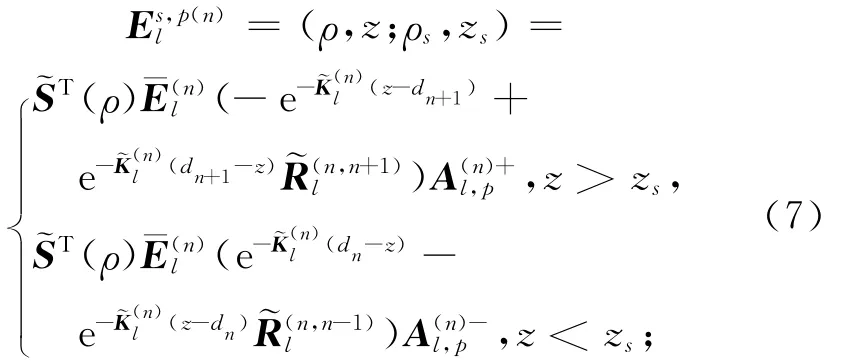
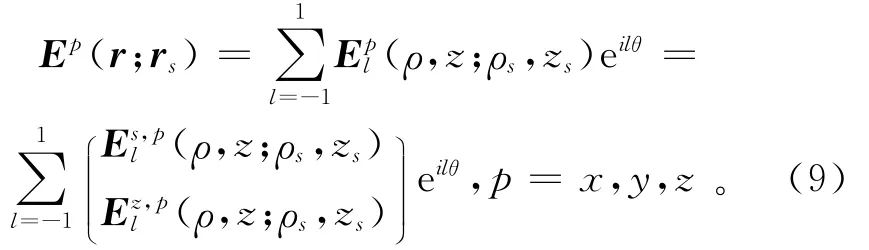
方程（3）中磁流源并矢Green函數珚GME（r，rR）可用同樣的方法得到，其3個列向量gq（r；rR），q＝x，y，z3個不同方向正交發射線圈，具有與方程（9）類似的表達式：

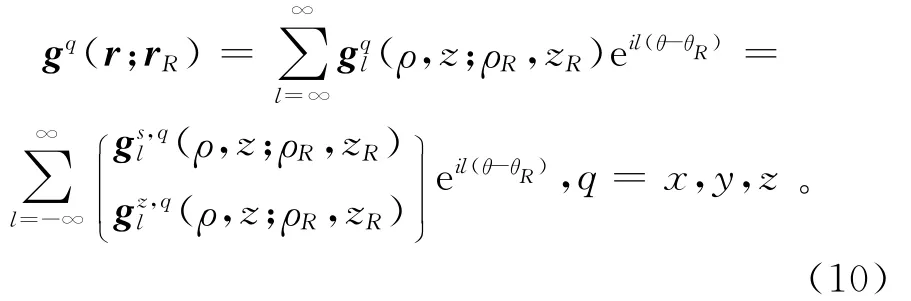
由于接收點rR可能不在井軸上，方程（10）右端是無限多個調和分量的和，將方程（9）和（10）代入方程（4）后，得

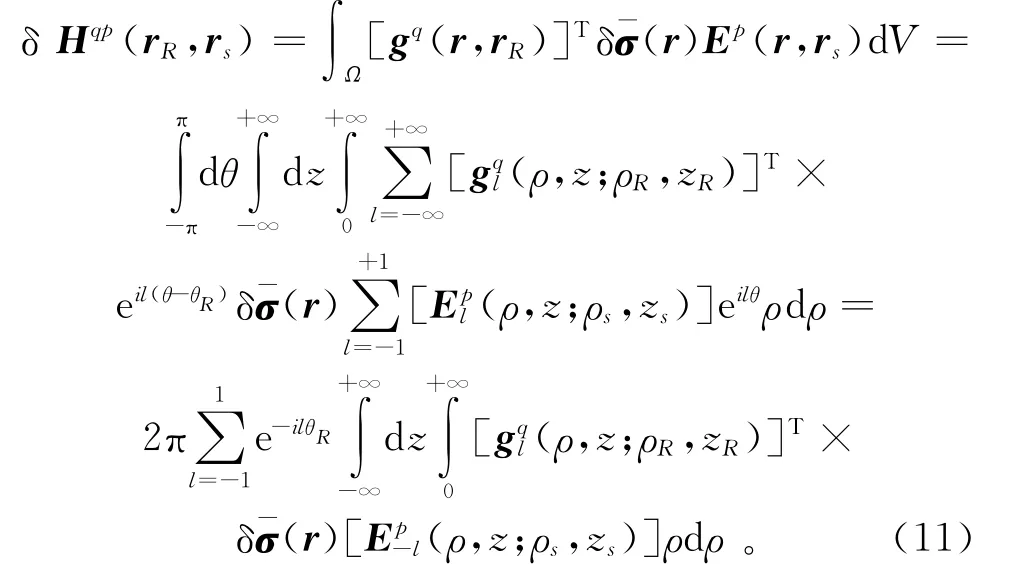
此外，將方程（5）代入方程（11）并經簡單整理，則方程（11）右端項中的被積函數可展開成如下表達式：

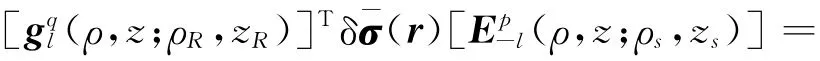
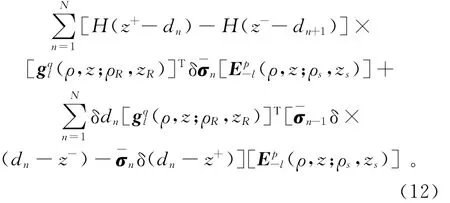
所以方程（11）右端的整個積分可簡化為

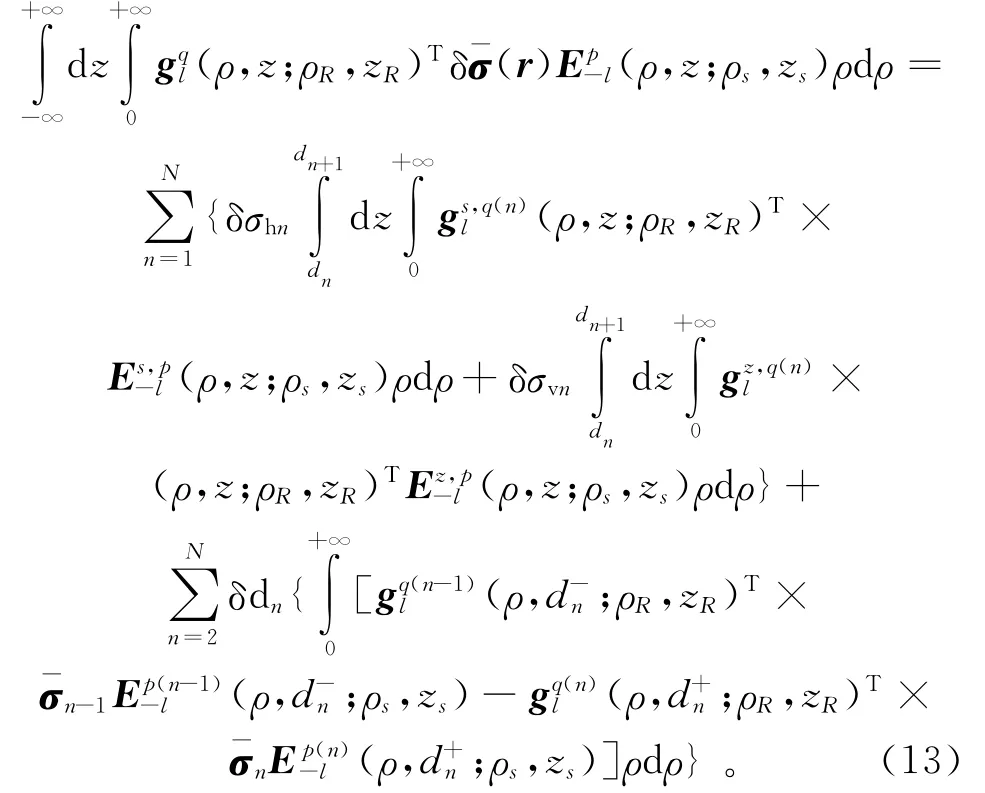
通過方程（7）和（8）得到的半解析式，方程（13）的右端項中關于z的積分可以解析得到，而關于ρ的積分可數值計算且積分與源點和接收點的位置無關，所以可事先計算并儲存起來以提高積分效率［9，11］。一旦計算出方程（13）中的各個積分，并代入方程（11）中，就能夠得到磁場變化與模型向量攝動方程：

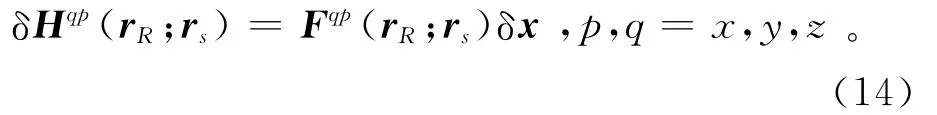
其中：p和q分別表示發射線圈和接收線圈的方向；Fqp（rR；rs）是磁場Hqp（rR；rs）相對于模型向量x的Frèchet導數。取方程（14）中3個主分量的虛部后再除以相應的儀器常數，就得到了多分量感應測井3個主視電導率變化與模型向量攝動方程：

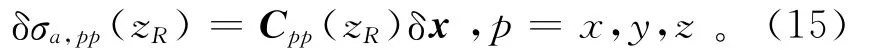
其中，Cpp（zR）是記錄點zR處的多分量感應測井視電導率對模型向量的Fréchet導數。由于模型參數δx中包含有電導率和層界面2個不同物理量綱的物理量，為便于反演計算，采用規范化處理技術將所有變量轉化為無量綱的純數：

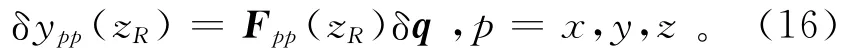
其中：δq＝（δqσ，δqh）T是模型向量的相對變化量，且δqσ＝（δσh，1／σh，1，…，δσh，N／σh，N，δσv，1／σv，1，…，δσv，N／ σv，N），δqh＝（δh2／（h3－h2），δh3／（h4－h2）／2，…，δhN－1／（hN－hN－2）／2，δhN／（hN－hN－1））；而δypp（zR）＝δσa，pp（zR）／σa，pp（zR）是視電導率的相對變化；Fpp（zR）＝σ－1a，pp（zR）Cpp（zR）Q是規范化Fréchet導數，且

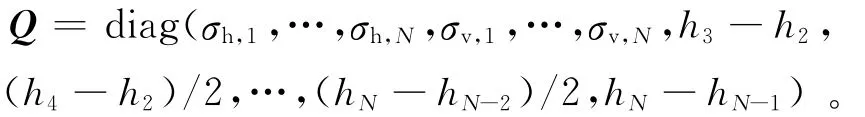
1.2 迭代反演

對于水平層狀各向異性地層，在井眼垂直情況下，視電導率σa，xx和σa，yy完全相同且它們與地層的縱橫向電阻率有關，而視電導率σa，zz僅反映地層水平電導率變化。所以從多分量感應測井資料中提取地層電阻率可以采用2種不同的處理方法：一種是先對σa，zz進行迭代反演確定出水平電導率，然后再進一步用σa，xx反演地層縱向電導率；另一種方法是將視電導率σa，xx和σa，zz結合在一起，同時反演縱橫向電導率和層界面。對于前一種反演方法，由于水平電導率的反演誤差會對縱向電導率的反演結果造成較大影響，所以筆者采用后種方法。

設Y0＝（）T是多分量感應測井儀器測量出的一系列視電導率σa，xx和σa，zz組成的向量，反演目的就是找出某個模型向量x0，使其理論模擬記錄Yc能夠最佳擬合于Y0。由于測井記錄是模型向量x的非線性函數，利用線性化方程（16）可以得到反演結果的迭代解［12］：

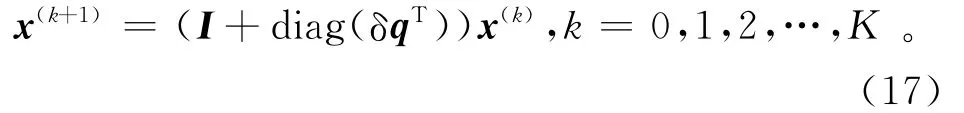
其中：x（0）是模型向量的初值；x（k）是第k次迭代反演結果；“I”是單位矩陣；“k”是預定的迭代總次數，實際數值實驗表明，通常情況下迭代8次就足夠了。而向量δq（k）是方程（16）的廣義解：

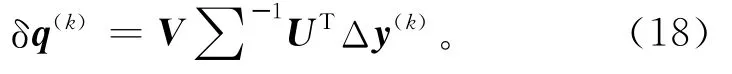
其中：Δy（k）＝diag（Y0－1）（Y0－Y（k））是理論測井記錄與輸入資料之間的相對誤差；F（k）＝U∑VT＝V∑－1UT是（16）式中規范化處理后的Fréchet導數矩陣的SVD分解。

2 數值結果

為檢驗上述反演方法的有效性，對理論模型數值模擬結果進行了反演。在反演過程中，儀器的源距L＝1m，源的發射頻率f＝20kHz，即僅考慮單發單收這種最簡單情形。

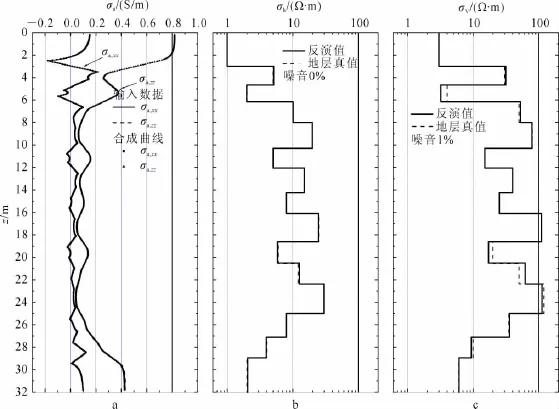
圖2 無噪聲多分量感應測井資料的反演結果Fig.2 The inversion results from noiseless multicomponent induction logging data from 15layer formation

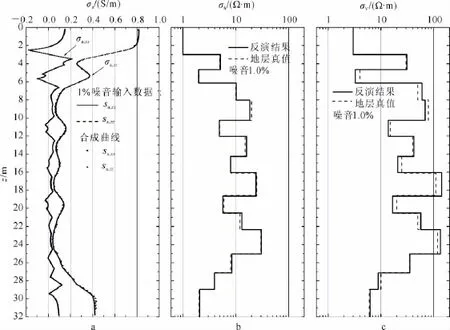
圖3 含1%噪聲多分量感應測井資料的反演結果Fig.3 The inversion results from 1%noise multicomponent induction logging data from 15layer formation

模型由15個各向異性層狀地層組成，從上到下各個地層的縱向電阻率分別是：3、30、4、50、80、15、40、25、110、20、50、120、35、10、6Ω·m，橫向電阻率：1、5、2、10、20、5、15、8、25、6、12、30、8、4、2Ω·m。13個層厚：1.65、1.50、1.85、2.30、1.75、2.20、1.85、2.50、1.95、1.80、2.65、2.10、1.85m。對于該模型首先通過正演軟件計算出視電導率曲線σa，xx和σa，zz，并作為反演計算的輸入數據（采樣間距0.05m）。反演前，假定各個地層縱橫向電阻率的初值是其真值的1／3，而各個地層界面的初值由公式h（0）n＝hn＋（hn＋1－hn－1）確定，由此得到的地層厚度的初始誤差約為20%。

圖2給出了迭代8次以后的反演結果。不難看出，所有結果均吻合得很好。但縱向電阻率的反演誤差比橫向電阻率大，說明縱向電阻率較難反演；此外，與常規的感應測井反演結果不同，在多分量的反演結果中似乎低電阻層上的反演誤差更大，說明縱向電導率大的地層其參數更難計算。

為了進一步檢驗反演方法的抗噪能力，圖3給出了在輸入數據中加入1%白噪聲后的反演結果。圖3a的結果顯示，反演模型的合成數據與輸入資料仍然吻合得較好；而圖3b和3c表明，反演結果與地層真值也很接近，但與無噪聲情況相比，反演誤差有了明顯增加，此外，縱向電阻率的反演誤差也增加得更為明顯。這里需要特別指出的是，反演結果的抗噪能力不僅與反演算法有關，還與模型參數密切相關：當地層厚度較大時，式（16）中磁場相對于該層參數的Frechet導數將比較大，這時其相應的抗噪能力也會更強。

3 結論

1）在薄交互層上，多分量感應測井資料中共面視電導率雖然存在負響應，但由于這種響應與地層參數間具有確定性關系，所以利用迭代反演算法仍然可以快速重構各向異性電阻率和層界面位置。

2）數值結果顯示，地層橫向電阻率比縱向電阻率更容易反演，其反演結果的抗噪能力也比縱向電阻率更強。

3）與常規的感應測井反演結果不同，在多分量反演結果中似乎低電阻層上的反演誤差更大，說明縱向電導率大的地層其參數更難計算。

（References）：

［1］ Michael Z，David K，Ertan P.Foundation of the Tensor Induction Well Logging［J］.Perophysics，2001，42（6）：588－610.

［2］ 汪宏年，陶宏根，姚敬金，等.用模式匹配算法研究層狀各向異性傾斜地層中多分量感應測井響應［J］.地球物理學報，2008，51（5）：1591－1599.

Wang Hong－nian，Tao Hong－gen，Yao Jing－jin，et al.Study on the Response of Multicomonent Induction Logging Tool in Deviated and Layered Anisotropic Formations by Using Numerical Mode Matching Method［J］.Chinese Journal of Geophysics，2008，51（5）：1591－1599.

［3］ 汪宏年，胡平，陶宏根.水平層狀非均質橫向同性地層中陣列多分量感應測井響應的快速計算［J］.地球物理學報，2012，55（2）：717－726.

Wang Hong－nian，Hu Ping，Tao Hong－gen，et al.Fast Algorithm of Responses of Array Multicomponent Induction Logging Tool in Horizontally Stratified Inhomogeneous TI Media［J］.Chinese Journal of Geophysics，2012，55（2）：717－726.

［4］ Wang Hong－nian，Tao Hong－gen，Yao Jing－jin.An Efficient and Reliable Simulation of Multicomponent Induction Logging Response in Horizontally Stratified Inhomogeneous TI Formations by Numerical Mode－Matching Method［J］.Geoscience and Remote Sensing，DOI：10.1109／TGRS.2012.2183135.

［5］ 姚東華，汪宏年，楊守文，等，用傳播矩陣法研究層狀正交各向異性地層中多分量感應測井響應［J］.地球物理學報，2010，53（12）：3026－3037.

Yao Dong－hua，Wang Hong－nian，Yang Shou－wen，et al.Study on the Responses of Multi－Component Induction Logging Tool in Layered Orthorhombic Anisotropy Formations by Using Propagator Matrix Method［J］.Chinese Journal of Geophysics，2010，53（12）：3026－3037.

［6］ 楊守文，汪宏年，陳桂波，等.傾斜各向異性地層中多分量高頻電磁波測井響應的三維時域有限差分（FDTD）算法［J］.地球物理學報，2009，52（3）：833－841.

Yang Shou－wen，Wang Hong－nian，Chen Gui－bo，et al.The 3－D Finite Difference Time Domain（FDTD）Algorithm of Response of Multi－Component Electromagnetic Well Logging Tool in a Deviated and Layered Anisotropic Formation［J］.Chinese Journal of Geophysics，2009，52（3）：833－841.

［7］ Wang Hong－nian，So Poman，Yang Shou－wen，et al.Numerical Modeling of Multicomponent Induction Well Logging Tools in the Cylindrically Stratified Anisotropic Media［J］.Geoscience and Remote Sensings，2008，46（4）：1134－1146.

［8］ Zhang Zhiyi，Yu Liming，Mauser K B.Simultaneous Determination of Relative Angles and Anisotropic Resistivity Using Multicomponent Lnduction Logging Data［J］.Geophysics，2004，69（4）：898－908.

［9］ Wang Hong－nian，Tao Hong－gen，Yao Jing－jin，et al.Fast Multiparameter Reconstruction of Multicomponent Induction Well Logging Datum in Deviated Well in a Horizontally Stratified Anisotropic Formation［J］.Geoscience and Remote Sensings，2008，46（5）：1525－1534.

［10］ Wang Hong－nian.Adaptive Regularization Iterative Inversion of Array Multicomponent Induction Well Logging Datum in a Horizontally Stratified Inhomogeneous TI Formation［J］.Geoscience and Remote Sensing，2011，49（11）：4483－4492.

［11］ Wang Hong－nian.Simultaneous Reconstruction of Geometric Parameters and Resistivity from the Multiarray Induction Log in a Horizontally Layered Formation［J］.Geoscience and Remote Sensing，2003，41（1）：185－194.

Simultaneously Fast Reconstruction of Resistivities and Interfaces in Horizontally Stratified TI Formation by Using Multicomponent Induction Well Logging Data

Wang Hong－nian1，Shang Qing－long1，Zhu Tian－zhu1，Li Zhou－bo2

1.College of Physics，Jilin University，Changchun 130012，China 2.College of GeoExploration Science ＆Technology，Jinlin University，Changchun 130026，China

We advance an efficient method to simultaneously reconstruct the horizontal and vertical resistivities and the interface depth each bed in the horizontally stratified transversely isotropic（TI）formation from the multicomponent induction well logging（MCIL）data.We first give the perturbed equation of electromagnetic（EM）fields，relation of conductivity function to the model parameters and the semi－analytic solutions of EM tensor Green function provided by the numerical mode matching method in the horizontally layered TI formation，and further set up a fast algorithm of Frèchet derivatives of multicomponent induction logging response with respect to all the formation resistivities and interfaces.Then，by combination of normalization and singular value decomposition（SVD）technique，we advance an iterative method to simultaneously reconstruct both horizontal and vertical resistivities and interface per bed so that we realize the best fit of the input data with the modeling logs.Numerical tests validate the algorithm.

induction logging；fast algorithm of Frèchet derivatives；reconstruction of resistivitiesand interface at same time

book=2012,ebook=678

P631.81

A

1671－5888（2012） 04－0900－06

2012－04－18

國家自然科學基金項目（40874058）

汪宏年（1962－），男，教授，博士生導師，主要從事非均質與各向異性介質中電磁場數值模擬與反演研究，E－mail：wanghn＠mail.jlu.edu.cn。