ND樣本最近鄰密度估計的一致強相合性

劉艷，吳群英

（桂林理工大學理學院，廣西桂林541004）

ND樣本最近鄰密度估計的一致強相合性

劉艷，吳群英

（桂林理工大學理學院，廣西桂林541004）

設X1，X2，…，Xn是同分布的負相依（ND）樣本，具有共同的密度函數f（x），利用相應的Bernstein不等式，將負相關（NA）樣本最近鄰密度估計的一致強相合性推廣到ND樣本，得到其最近鄰密度估計的一致強相合性.

負相依序列；最近鄰密度估計；一致強相合性；Bernstein不等式

概率密度估計和非參數非線性回歸是非參數估計中兩大問題.最近鄰密度估計（NN－估計）是由Loftsgarden和Quesenberry［1］于1965年提出的.設X1，X2，…，Xn是來自未知密度f的樣本，先選定一個與n有關的整數k＝kn，1≤k＜n，對固定的x∈R，記an（x）為最小的正數a，使得［x－a，x＋a］中至少包含X1，X2，…，Xn中的k個.注意到，對每一個a＞0可以期望在X1，X2，…，Xn中大約有2anf（x）個觀察值落入區間［x－a，x＋a］中.因而值f（x）的估計（記為＾fn（x））自然地可以通過令k＝2an＾fn（x）得到.于是定義＾fn（x）＝k／2nan（x）為f（x）的估計.此后，許多著名學者都討論過它的性質.對于獨立樣本，Wagner［2］證明了NN－估計的強相合性，陳希孺［3］證明了它的漸近正態性，而楊善朝［4］在一定條件下給出了NA序列下NN－估計的相合性.ND相依序列是比NA相依序列弱的一種數列，這些負相依隨機變量的概念在可靠性理論、滲透理論和多元統計分析中均有廣泛的應用.因此，將獨立序列或NA序列的一些性質推廣到ND序列是十分必要的.文獻［5－7］分別討論了ND序列完全收斂性、ND隨機變量列的指數不等式等，但卻很少觸及NN－估計.而NN－估計在獨立樣本下已有很多優點，特別是計算簡單，容易實施.因此，在ND樣本下也應有一定的地位.本文在ND序列的基礎上，討論了ND序列的最近鄰密度估計的一致強相合性.

1 定義及引理

假設總體X的分布密度函數為f（x），X1，X2，…，Xn是抽自該總體的ND樣本；F（x）是密度函數f（x）相應的分布函數，是樣本X1，X2，…，Xn的經驗分布函數；c是與n無關的常數，在不同的地方可以表示不同的值.

定義1［5］稱隨機變量X1，X2，…，Xn，n≥2是ND的，若對?x1，x2，…，xn∈R，都有

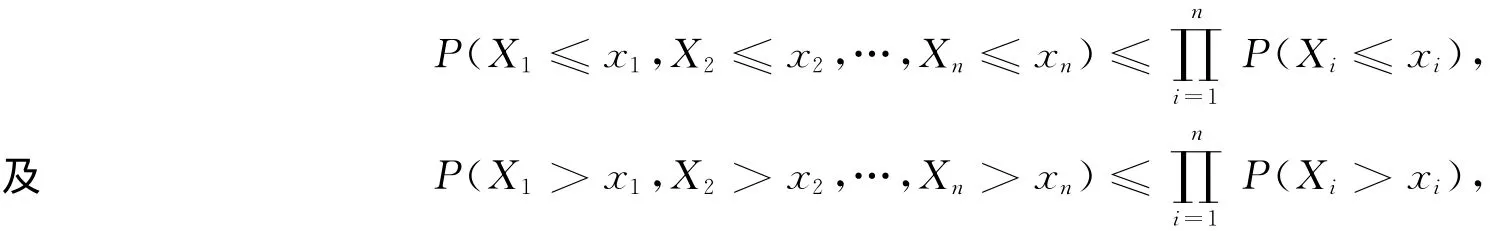
稱隨機變量列｛Xn；n≥1｝是ND列，如果對任意的n≥2，X1，X2，…，Xn是ND的.

從有限總體不放回抽樣所得到的樣本不是獨立的，但是ND的.

引理1［5］設｛Xn；n≥1｝是ND的，?m≥2，A1，A2，…，Am是集合｛1，2，…，n｝的兩兩不交非空子集.如果fi（i＝1，2，…，m）是對每個變元都非降（或非升）的函數，則f1（Xj；j∈A1），f2（Xj；j∈A2），…，fm（Xj；j∈Am）仍是ND的.

2 主要結果

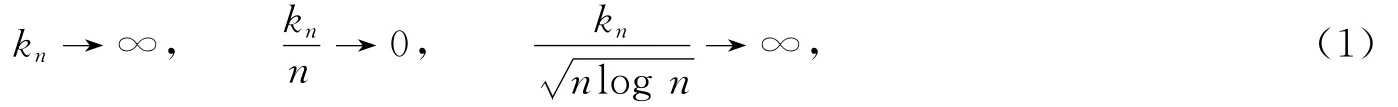
且f（x）在R上一致連續，則有

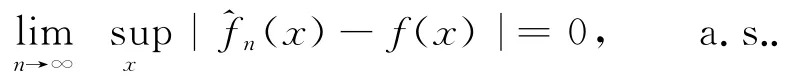
定理1 設｛Xn；n≥1｝是ND序列，kn滿足

證明 ?ε＞0，P｛｜＾fn（x）－f（x）｜＞ε｝＝P｛＾fn（x）＞f（x）＋ε｝＋P｛＾fn（x）＜f（x）－ε｝，當f（x）＜ε時，f（x）－ε的值為負值，由＾fn（x）的非負性知，事件｛＾fn（x）＜f（x）－ε｝是不可能事件，故其概率為零.因此，對P｛＾fn（x）＜f（x）－ε｝的估計，只需考慮f（x）≥ε的情況.

3 應用舉例

設在可靠性問題中r.v.X的分布函數記為F（x），密度函數為f（x），生存函數和失效率函數分別定義為Fˉ（x）＝1－F（x）＝P（X≥x）和r（x）＝.又設X，X，…，X為從總體F（x）中抽取的同分12n布ND樣本，則生存函數和失效率函數的自然估計為

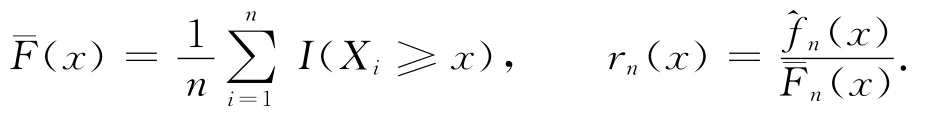
定理2 設定理1的條件滿足，則對任何滿足F（c）＜1的c，均

證明 記ˉFn（x）＝1－F（x），ˉFn（x）＝1－Fn（x），顯然有

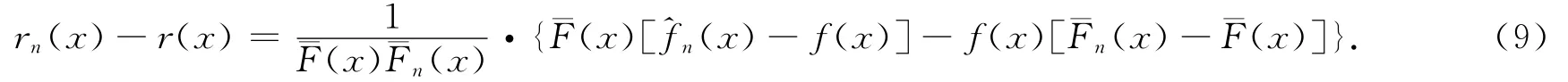
注意到0＜Fˉ（c）≤Fˉ（x）≤1，?x≤c，sup f（x）≤M＜∞.由定理1和引理4知，sup｜＾fn（x）－f（x）｜→

xx≤c0，a.s.，而且從而當n充分大時，對于x≤c，一致地有Fˉ（c）＞Fˉ（x）－Fˉ（c）／2＞Fˉ（c）／2＞0.由這些事實和式（9）即得定理2的結論.證畢.

［1］ LOFTSGARDEN D O，QUENSBERRY C D.A Nonparametric estimator of a multivariate density function［J］.Ann Statist，1965，36（3）：1049－1051.

［2］ WAGNER T J.Strong consistency of a nonparametic estimate of a density function［J］.IEEE Trans Systems Man Cybenet，1973（3）：289－290.

［3］ CHENG Xi－ru.Convergence rates for nearest neighbor density estimator［J］.Sci China Ser A，1980（12）：1419－1428.

［4］ YANG Shan－chao.Consistency of nearest neighbor density function for pairwise NA sequence［J］.Acta Math Application，2003，26（3）：385－395.

［5］ BOZORGNIA A，PATTERSON R F，TAYLOR R L.Limit theorems for ND r.v.′s［R］.Athens：University of Georgia，1993.

［6］ WU Qun－ying，JIANG Yuan－ying.The strong consistency of estimator in linear model for negatively dependent random samples［J］.Communications in Statistics－Theory and Methods，2011，40（3）：467－491.

［7］ 楊善朝.NA樣本最近鄰密度估計的相合性［J］.應用數報，2003，26（3）：385－408.

Uniform Strong Consistency of Nearest Neighbor Estimator of Density Function for Negative Dependent Samples

LIU Yan，WU Qun－ying
（College of Science，Guilin University of Technology，Guilin 541004，China）

Suppose that X1，X2，…，Xnare negative dependent（ND）samples，with a common density function f（x）.By the use of the corresponding Bernstein inequality，the uniform strong consistency of nearest neighbor estimator of density function for negatively associated（NA）samples is extended to ND samples，and the latter uniform strong consistency of nearest neighbor estimator of density function is obtained.

negative dependent sequence；nearest neighbor density estimator；Bernstein inequality

O 212.7

A

（責任編輯：黃曉楠 英文審校：黃心中）

1000－5013（2012）05－0590－05

2012－01－07

吳群英（1961－），女，教授，主要從事概率統計的研究.E－mail：wqy666＠glite.edu.cn.

國家自然科學基金資助項目（11061012）；廣西自然科學基金資助項目（2011GXNSFA018147）；廣西研究生教育創新計劃項目（2011105960202M32）