對教育裝備均衡指數的研究*

艾倫 興喬

1 首都師范大學 北京 100048 2 中國教育技術裝備雜志社 北京 100081

使用基尼系數法固然可以對教育裝備均衡性進行測量與評價，但并不是最佳的，且存在諸多不便和不適。本文提出一個全新的概念——教育裝備均衡指數J，并說明用其對教育裝備均衡性進行測量評價的可行性與優越性。

1 一個基本假設

在《中國教育技術裝備》雜志2012年第29期刊出的《話說裝備（六）——教育裝備投入均衡性的基尼系數表示法》一文中，筆者論述了用反映社會分配平等或不平等水平的基尼系數來表示教育裝備投入均衡性的可能性與存在的問題。對于社會分配問題和教育裝備均衡問題，筆者認為它們都符合這樣一個規律：隨著社會的發展和人們的努力，社會將會達到絕對的分配平等，即人人收入一樣，實現“世界大同”；而教育裝備的投入也同樣會逐漸達到均等與均衡。這是一個必然發展的趨勢，也是本文中提出的一個基本假設。如果用熵函數來描述這一現象的話，上述諸過程都是“熵增”過程。

2 熵函數表示均衡性的原理

社會分配均等和教育裝備均衡的發展規律，就像一個封閉的熱力學系統一樣，其中物體的熱總是具有從溫度高的地方向溫度低的地方擴散的趨勢，當各處的溫度都相同時，系統的一個物理量即熵的值最大（不可逆過程），被稱為熱力學的“熵增原理”。信息的傳播也有相同的特點，信息從信源向外傳播的過程中信息熵在增加，當系統中所有信宿都得到該信息時，系統具有最大的信息熵，被稱為信息學的“熵增原理”。在《中國教育技術裝備》雜志2010年第12期刊出的《電子白板教學的局限性》一文中，筆者論述了教育信息傳播時也有相同的情況，當知識只存在于教師頭腦中時，教學系統的信息熵為0；而通過教育信息傳播使系統中所有學生都相同地掌握了教師的知識時，系統具有最大的信息熵。所以，教學過程就成為信息熵增加的過程，且總具有增加的趨勢，稱其為教育信息的“熵增原理”。于是可以猜想到，用熵函數也是可以反映教育裝備投入均衡性的，當達到絕對均衡時，可以得到最大的熵函數值。

3 教育裝備均衡指數J的表達與算法

信息系統是一個離散系統，它的熵函數表達為：

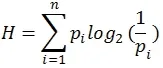
式中的n表示系統中事件的總數，pi則表示第i個事件發生的概率。當系統中僅有1個必然事件（如：i=1）發生時，有p1=1，p2=…=pn=0，系統有最小的熵：Hmin=0；而當系統中的n個事件等概率發生時，有p1=p2=…=pn=1/n，系統達到最大熵：Hmax=log2n。則系統的熵函數值就應該分布在0與log2n之間。如果使用熵函數值直接當作教育裝備均衡性測量的指數，就會存在一些問題。例如：基尼系數G的數值應該分布在0～1之間[1]，而熵函數值不能夠滿足這一點。于是，筆者將熵函數H歸一化后用來反映教育裝備的均衡性，得到表達式：

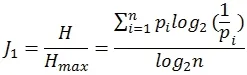
式中的pi即為第i個學校生均教育裝備數占全部生均教育裝備數總和的比例，n為學校總數；而J1的值則變得在0～1之間了。

但是，通過演算可以知道，當基尼系數G=0時所對應的是J1=1，基尼系數G=1時對應J1=0，所以重新定義：

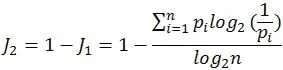
則J2與基尼系數G就有了取值一致的對應關系。

進一步分析可知，由于基尼系數表達式為：

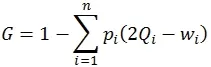
其中pi與G是線性關系，而J2的表達式中pi與J2呈非線性關系。通過演算發現J2的數值在正常情況下分布在很小的數值區間內。綜合考慮之后，定義：

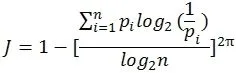
此式可以很好地反映教育裝備配備均衡性的情況，本文稱J為教育裝備均衡指數。

利用上述教育裝備均衡指數J的表達式，通過電子表格Excel來自動計算教育裝備的均衡性，將使其變得十分容易。

1）打開Microsoft Office Excel，建立一個新的工作表。

2）在該工作表的A1、B1、C1、D1和E1單元格內分別鍵入“經費數”“學生數”“生均經費”“pi”和“pi*log2(1/pi)”（如圖1所示）。

3）在A3至A13和B3至B13單元格內輸入非0的任意正數（注：為了說明方便，本例只處理11組數據，即n=11；需要處理更多數據，可根據需要加長該表格，并注意n值的改變）。

4）在C3單元格內輸入公式“=A3/B3”，點擊“√”按鈕；將鼠標光標放在C3單元格的右下角，鼠標光標變成“+”，按住鼠標左鍵向下拖鼠標至C13單元格處，放手。C4的內容將變成“=A4/B4”，C5的內容變成“=A5/B5”，依此類推。

5）在D3單元格內輸入公式“=C3/C$14”，點擊“√”按鈕，然后參照4）中的操作對D3至D13進行處理。

6）在E3單元格內輸入公式“=D3*LOG(1/D3,2)”，點擊“√”按鈕，然后參照4）中的操作對E3至E13進行處理。

7）在A14單元格內輸入公式“=SUM(A3:A13)”，點擊“√”按鈕；將鼠標光標放在A14單元格的右下角，鼠標光標變成“+”，按住鼠標左鍵向右拖鼠標至E14單元格處，放手。

8）在E15單元格內輸入公式“=1-(E14/LOG(11,2))^(2*PI())”，則該單元格內就是教育裝備均衡指數J的數值。

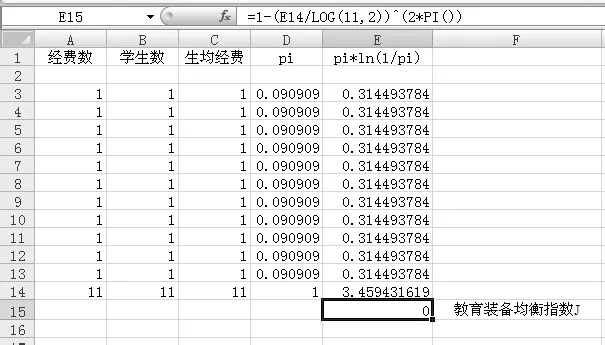
圖1 計算J的Excel表格

4 教育裝備均衡指數J與基尼系數G對比分析

筆者利用全國32個省、直轄市、自治區2006～2011年小學校教育裝備投入的數據（數據來源：教育部教育管理信息中心）進行教育裝備均衡指數J與基尼系數G的計算，并將結果制成圖像（如圖2所示，系列1為J的變化趨勢線，系列2為G的變化趨勢線）。從圖2中可以看出，兩條曲線的一致性還是比較好的，只是J的數值在0.7上下浮動，且分辨率比較高，而G的數值在0.4上下浮動，分辨率比較低。

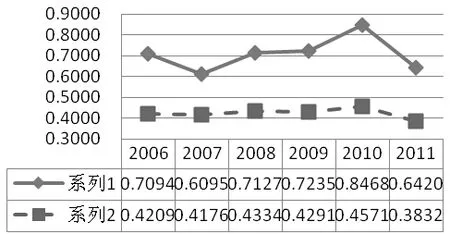
圖2 J與G的對應關系

為了說明使用均衡指數J表示教育裝備的均衡性比使用基尼系數G具有更大的優勢，下面將一些特殊數據的J和G進行對比，并指出它們的差異和優略。

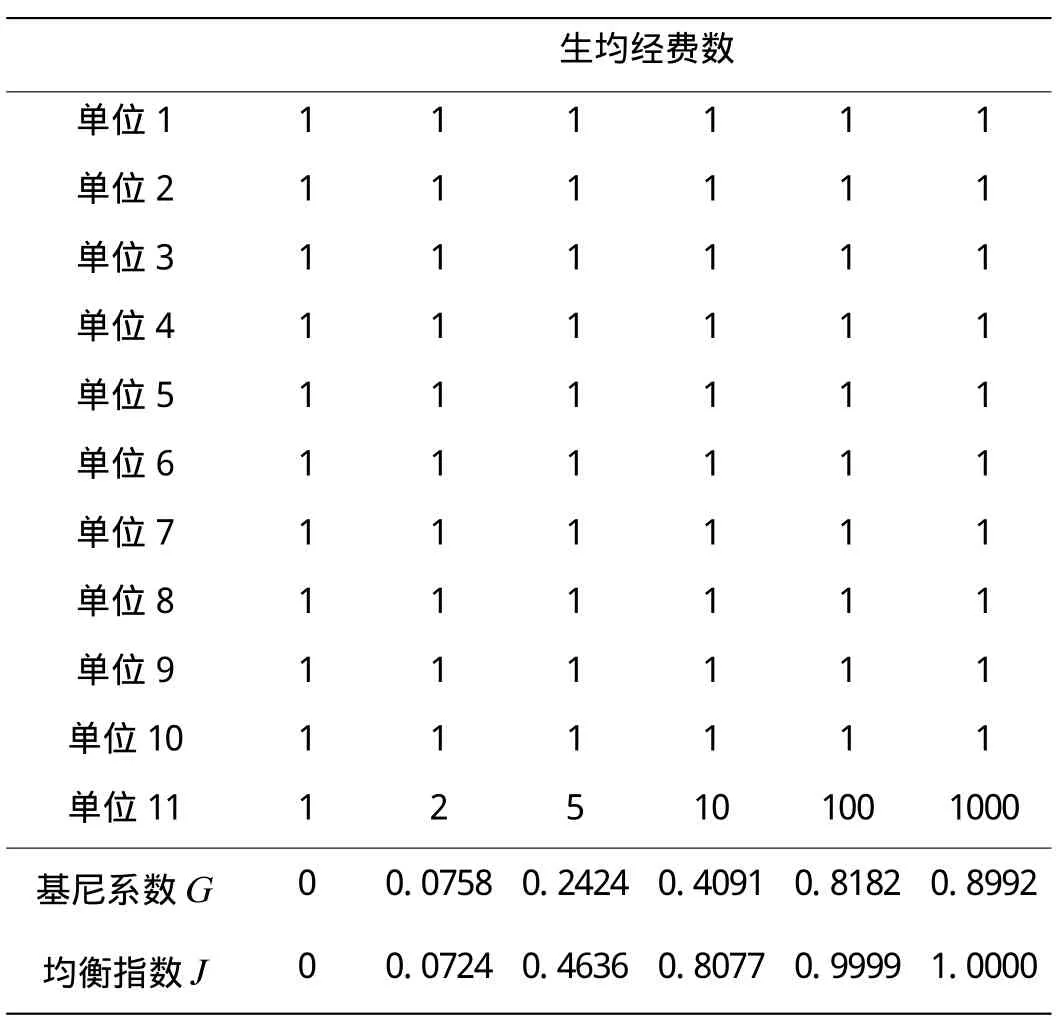
表1 J與G的邊界值比較

表1開列的數據反映出，在絕對均衡或平等的情況下有J=G=0，這一點與所期望的結果是一樣的。當不均衡現象出現時，隨著不均衡度的加劇，J比G以更快的速度向最大值1趨近。這一點正好能夠反映出，人們在教育裝備配備上與社會人均收入相比，更加不能容忍某些單位與其他單位之間存在更大、更懸殊的投入比例。

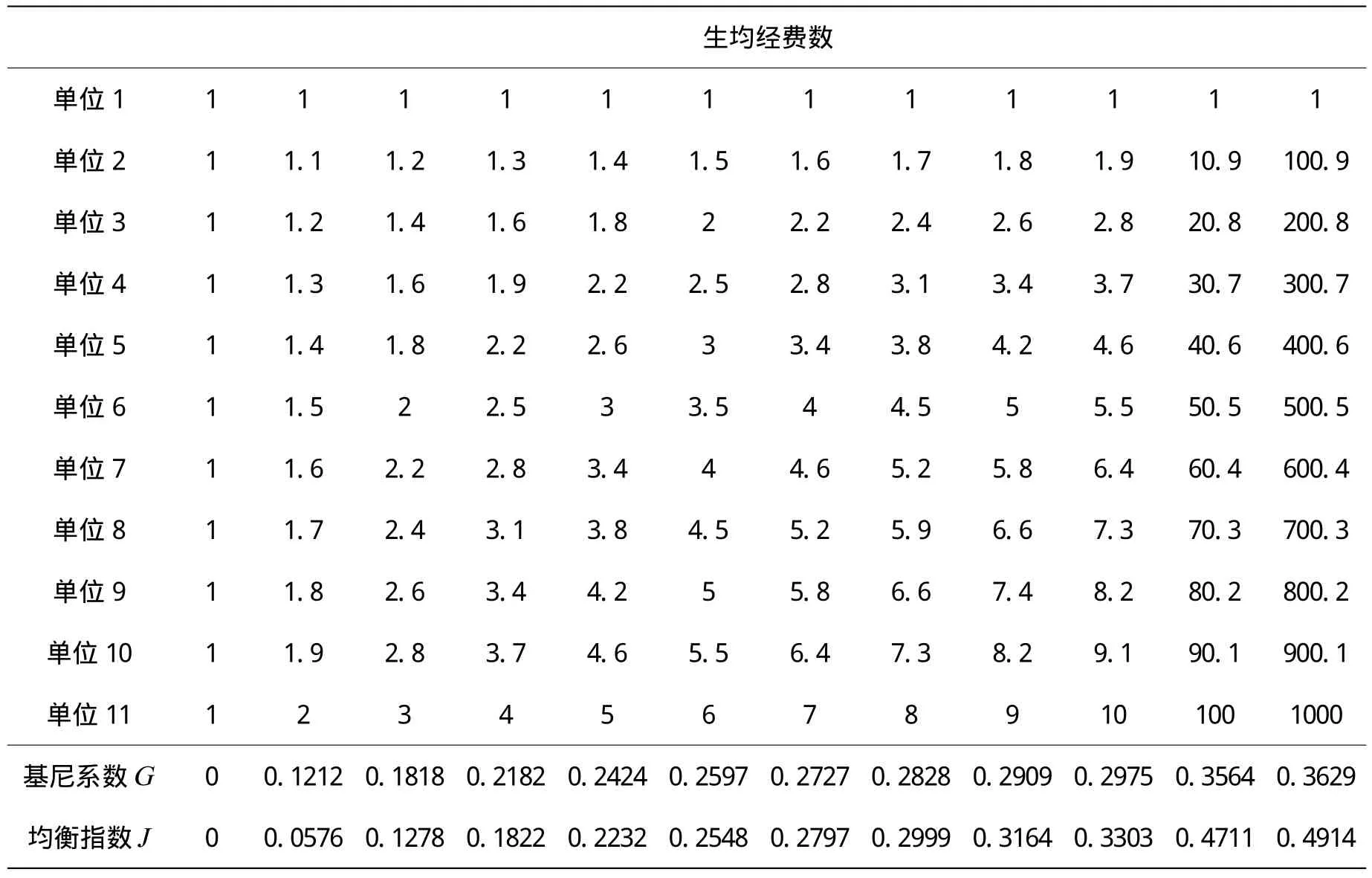
表2 J與G的漸變值比較

表2開列數據反映出的問題將更有意義。這些數據的分布呈現出所謂的“棗核狀”，即最“貧”與最“富”的數量極少，絕大部分為“中產階級”。一般認為，這種分布對于社會分配是一種表現比較好的現象，可以使得社會穩定，即使最“貧”與最“富”的收入比例相差十分懸殊也不必顧忌。所以基尼系數對“貧富”比例達到1000倍的情況，仍然賦予0.3629的好成績（基尼系數在0.3～0.4之間，收入相對合理[2]）。而教育裝備均衡指數J對此表現出不能夠過于容忍的態度，J=0.4914，已經接近“差距懸殊”的范圍（基尼系數在0.4～0.5之間，收入差距較大；達到0.5以上則屬于收入差距懸殊[2]）。在實際情況中，教育裝備的投入也是不能夠容忍這樣巨大的比例差距出現的。所以，在教育裝備研究領域，采用均衡指數J要比使用基尼系數G有更大的優越性。

綜合上述情況可以看出：1）均衡指數J比基尼系數G的計算方法更加簡單，概念更加清晰；2）用均衡指數J來測量評價教育裝備的均衡性，比使用基尼系數G更加接近實際情況；3）用均衡指數J來測量評價教育裝備的均衡性時，其數值標準可仍然采用基尼系數的規定（數值低于0.2，屬于均衡性好；在0.2～0.3之間，為均衡性比較好；在0.3～0.4之間，均衡性相對合理；在0.4～0.5之間，均衡度差距較大；達到0.5以上則屬于均衡度差距懸殊）。

5 結語

無論使用均衡指數J還是使用基尼系數G來評價教育裝備的均衡性，其實都存在一些必須進一步深入進行研究的問題。例如，使用J或G測量教育裝備經費投入，就會遇到這樣的問題：假設這些經費是用來建筑校舍的，由于全國各地材料、勞動力等成本的差異，同樣多的經費會產生差距很大的校舍面積及水平，于是其發揮的實際作用將非常不同。所以在評價時測量生均教育裝備數比測量生均經費數顯得更加合理。但是，進一步分析可知，測量生均教育裝備數也存在許多問題，如生均教室面積、生均實驗室面積、生均圖書數、生均計算機數等，它們在測量時的權重應該是不一樣的，如何對它們進行科學的加權是一個非常復雜的問題。再如，生均計算機數有時也不能反映真實情況，計算機可能是286級別的，也可能是Core級別的，如果再對它們進行加權，將使得問題更加復雜化。所以，教育裝備領域還有巨大的研究空間、龐雜的實際問題有待去鉆研。

[1]劉穎,等.對基尼系數計算方法的比較與思考[J].統計與決策,2004(9):15-16.

[2]基尼系數[EB/OL].[2012-10-05].http:baike.baidu.com/view/186.htm.