一種基于拓撲信息的多邊形數據自動生成算法

盧 浩，鐘耳順，王天寶，王少華

（1.中國科學院地理科學與資源研究所，北京100101；2.中國科學院研究生院，北京100039；3.北京超圖軟件股份有限公司，北京100015）

一種基于拓撲信息的多邊形數據自動生成算法

盧 浩1，2，鐘耳順1，3，王天寶1，2，王少華1，2

（1.中國科學院地理科學與資源研究所，北京100101；2.中國科學院研究生院，北京100039；3.北京超圖軟件股份有限公司，北京100015）

在GIS的眾多應用中，多邊形數據的自動生成和多邊形數據拓撲關系的構建與維護都是一種高頻率的操作。該文在分析和總結已有多邊形數據自動生成算法和拓撲關系生成算法基礎上，提出了一種基于拓撲信息的多邊形數據自動生成算法（PG－TI）。介紹了該算法的數據結構以及弧段鄰接關系確定、多邊形搜索和拓撲關系確定3個核心過程，重點探討了使用多邊形搜索過程中建立的拓撲信息來提升拓撲關系確定過程性能，在此基礎上與傳統算法和Arc GIS中對應算法的時間復雜度進行了對比分析和驗證。

地理信息系統；多邊形；拓撲信息；包含關系

0 引言

在GIS中，多邊形數據的自動生成是一種常用操作，而算法性能是研究的重點之一。多邊形邊界和區域內是多邊形數據的兩個基本組成部分，GIS軟件中的多邊形數據處理功能的完善和性能的提高均直接依賴于對這兩個基本要素的處理。例如：左轉算法的發現導致了多邊形拓撲信息生成的自動化，點與多邊形包含關系的判定定理使得島區判定實現了計算機處理［1］。在多邊形數據的自動生成過程中，一個重要的步驟是對于簡單多邊形數據間包含關系進行判定。齊華［2］給出了一個根據多邊形內點和面積排序的閉合邊界包含關系判定算法，該算法依賴于兩個判定：判定1（閉合邊界包含關系判定準則）：對于任意閉合邊界a、b，如果a上有任意一點位于b的內部，則a被b所包含；判定2（父邊界判定準則）：父邊界是對于內邊界滿足判定1的外邊界序列中面積最小的外邊界。該算法主要通過判斷多邊形內點與其它多邊形的空間位置關系得到多邊形包含關系，而沒有利用相關拓撲信息。

多邊形數據自動生成算法主要步驟總結為弧段鄰接關系確定、多邊形搜索、拓撲關系確定3個過程。相關研究有：閆浩文等［3］提出了基于方位角計算的多邊形自動生成算法，利用自動生成的內點進行點與多邊形包含關系的判定；梁曉文等［4］提出了基于夾角變化趨勢的多邊形自動生成算法，根據相鄰弧段夾角和判斷多邊形搜索方向，避免了無效多邊形的生成；李大軍等［5］在閆浩文［3］算法基礎上，提出了一種改進算法，只進行2 N（N為弧段數）次邊的搜索，即可搜索出所有的多邊形。但這些研究較少涉及包含關系判定過程的改進。本文提出了一種基于拓撲信息的多邊形數據自動生成算法（PG－TI），通過使用多邊形搜索過程中生成的弧段左右多邊形信息，將此拓撲信息解析后用于后續的多邊形包含關系判定中，使得多邊形生成效率有了較大提升。

1 空間拓撲關系

地理實體間的空間拓撲關系是一種不隨空間旋轉、平移、放大／縮小等變換而發生改變的定性空間信息［6］，反映了空間目標的邏輯關系，其對空間推理、查詢、分析等眾多空間操作具有重要意義。研究較多的確定性空間拓撲關系模型包括Egenhofer等在“四交模型”基礎上提出的“九交模型”［7］，Randell等運用區域演算理論來表達空間區域拓撲特性的空間邏輯模型［8］，Li等基于空間代數方法提出的空間代數模型［9］，吳建新等提出的基于Voronoi圖的混合方法（用空間對象的Voronoi區域作為其外部，對原模型進行了改進）［10］。

有學者將多邊形拓撲關系的建立過程歸結為：弧段結點的匹配和弧段連接關系的建立、同一結點上弧－弧拓撲關系的建立、閉合邊界弧段相鄰關系的建立以及閉合邊界包含關系的確定等步驟［2］。針對計算較為耗時的同一結點上弧－弧拓撲關系的建立，眾多學者提出了改進算法，包括使用泰勒級數展開近似值替代，使用函數Qi（x，y）［11］作為參數，基于計算幾何矢量外積的算法［12］。而對于較為復雜的閉合邊界包含關系確定過程研究和改進較少，本文則著重針對該過程進行基于拓撲信息的研究和改進。

2 改進算法描述

本文算法在弧段鄰接關系確定過程中，通過使用均勻網格索引來加速鄰接關系建立過程；在多邊形搜索過程中主要使用左轉算法，但會將弧段的左右多邊形信息同步記錄下來；由于左轉算法會生成一些無效多邊形，拓撲關系確定過程包括無效多邊形的剔除和拓撲包含關系的確定。

2.1 弧段鄰接關系確定

由于算法輸入為離散的弧段數據，首先需要建立弧段之間的鄰接關系，才可以進行后續的多邊形搜索。而鄰接關系的實質是公共結點的標識，因此該過程主要生成結點和弧段的雙向索引。定義如下數據結構：

（1）邏輯結點索引數組：

TNodeInfo［NodeCount］NodeIndex；

數組類型為邏輯結點信息結構體：

其中，nPos為構成此邏輯結點的弧段起始索引值，n Num為構成此邏輯結點的弧段數目，數組長度NodeCount為邏輯結點數目。

（2）弧段索引數組：

int［ArcCount＊2］ArcIndex；

其中，ArcCount為弧段數目，因為每個弧段包括起始和終止兩個結點，因此數組長度為弧段數目的二倍。

（3）弧段到邏輯結點索引數組：

int［ArcCount］ArcFromID；

int［ArcCount］Arc ToID；

NodeIndex和ArcIndex記錄邏輯結點到弧段的正向索引，其中NodeIndex為邏輯結點索引，因為每個邏輯結點都由一個或多個弧段的結點構成，則其需要記錄的是每個邏輯結點對應的多個弧段在弧段數組ArcIndex中的起始索引（多個弧段按照方位角排序）nPos以及弧段數目n Num。ArcIndex中記錄的是每個邏輯結點對應的弧段ID，如果為該弧段起始結點，則ID值為正，如果為終止結點，則ID值為負。ArcFromID和Arc ToID記錄弧段到邏輯結點的反向索引，即分別記錄每個弧段起始和終止結點對應的邏輯結點ID。索引結構如圖1所示。

圖1 弧段鄰接索引結構Fig.1 Arc adjacency index chart

圖1中，NodeIndex中每個元素對應一個邏輯結點，通過nPos和n Num可以索引到ArcIndex中對應此邏輯結點的一條或多條弧段ID（即圖1中的ArcID），通過ArcID可以索引到ArcFromID和Arc ToID數組中記錄的該弧段的起始和終止邏輯結點索引，即從ArcFromID和Arc ToID中通過弧段到邏輯結點的反向索引可以回到NodeIndex中。

弧段鄰接關系確定整體過程如下：1）建立均勻網格索引，并計算每條弧段起始和終止結點對應的索引位置；2）計算索引結點處對應的方位角（此處約定為從X正半軸起逆時針旋轉角度）和所歸屬的弧段一并存儲；3）遍歷均勻格網索引，進行結點匹配，由多個結點組成的邏輯結點按照方位角大小排序后將索引信息存入NodeIndex、ArcIndex、ArcFromID和Arc ToID結構中。

2.2 多邊形搜索

當弧段鄰接關系建立后，算法初始輸入的離散弧段已通過起始和終止結點坐標匹配為對應的邏輯結點，通過此邏輯結點和弧段組成的“邏輯網絡”即可進行多邊形搜索（圖2）。具體搜索過程為：1）假定起始邏輯結點為N1，則首先進行弧段A1搜索，通過A1到達邏輯結點N2后搜索到弧段A2，類似可以通過弧段A3后回到起始邏輯結點N1，此時構成閉合環路，生成多邊形N1N2N3N1。2）繼續以N1為起始結點搜索（逆時針尋找下一個弧段），此時處理弧段A5，到達結點N4后根據弧段順序處理弧段A7，依次搜索到弧段A8和A1后構成閉合環路，生成多邊形N1N4N5N2N1。3）繼續以N1為起始結點，搜索該邏輯結點最后一個弧段A3，類似過程1，可以得到多邊形N1N3N4N1，此時N1所有關聯弧段的左右多邊形都已生成。4）繼續處理下一個邏輯結點N2，因為A1的左右多邊形都已生成，則從A2弧段開始搜索，順次進行A2A8A63個弧段的搜索，生成多邊形N2N5N3N2，此時N2所有關聯弧段的左右多邊形都已生成。5）繼續處理下一個邏輯結點N3，生成多邊形N3N5N4N3，此時所有邏輯結點關聯的弧段左右多邊形都已搜索完畢，共生成5個簡單多邊形（面積最大的多邊形N1N4N5N2N1為無效多邊形）。

圖2 多邊形搜索示意Fig.2 Diagram of polygon search

2.3 拓撲關系確定

經過多邊形搜索過程，所有簡單多邊形都已生成，此時需要進行無效多邊形剔除和多邊形包含關系判定（用以組合為復雜多邊形）。齊華［2］給出的判定算法主要步驟為：1）將生成的簡單多邊形按照面積從小到大排序；2）從較小多邊形開始處理，計算出此多邊形內點，判定內點和其它多邊形的包含關系，從而得到該多邊形的父多邊形。

值得注意的是，在判定內點和其它多邊形的包含關系時，當生成多邊形數目較多時，容易產生大量的無效判定，導致整體判定效率較低；而通過解析多邊形搜索過程中記錄的每個弧段左右多邊形拓撲信息，可以提升判定效率。本文的主要思路是將離散的簡單多邊形根據其拓撲鄰接關系組成若干拓撲鄰接區域Tn（圖3），則可以基于這些拓撲鄰接區域判定拓撲關系，而不再基于多邊形搜索過程產生的大量簡單多邊形進行判定。

圖3 拓撲鄰接區域Fig.3 Topology adjacency area

如圖3所示，多個離散多邊形被劃分為T1、T2和T33個拓撲鄰接區域，簡單多邊形P被T3中的某個多邊形包含，但其本身不屬于任何拓撲鄰接區域（因為其邊界弧段沒有和其它多邊形共用），而拓撲鄰接區域具有如下優良性質：1）如果Pn∈Ti、Pm∈Tj且i＝j，則Pn和Pm不存在包含關系，即同屬一個拓撲鄰接區域的多邊形之間不存在包含關系；2）如果Pn∈Ti且Pn被P包含，則有Pm∈Ti且Pm被P包含，即一個拓撲鄰接區域中的多邊形被另一個多邊形包含，則此拓撲鄰接區域中的其它多邊形也被這個多邊形包含。換言之，包含關系判定只需要在不屬于任何拓撲鄰接區域的多邊形之間和該類多邊形與拓撲鄰接區域多邊形之間進行，且同一拓撲鄰接區域中的多邊形具有同樣的包含關系。

2.4 基于拓撲信息的判定算法

定義兩個數組int［ArcCount］Arc LeftPolygon和int［ArcCount］Arc RightPolygon，分別存儲每個弧段的左多邊形ID和右多邊形ID信息，在多邊形搜索過程中，可以同步生成并存儲每條弧度的左右多邊形信息。定義一個二維數組int［RegionCount］［Arcs］Region ArcsID，存儲構成每個多邊形的邊界弧段ID，第一維長度為多邊形數目。

算法整體流程如下：1）遍歷左右多邊形數組，將構成每個多邊形的弧段ID記錄到Region ArcsID中，其中從Arc LeftPolygon中讀取的記錄為正ID，從Arc RightPolygon中讀取的記錄為負ID。2）遍歷所有多邊形對象，使用一個棧結構進行廣度優先搜索，對共用公共弧段而同屬于某一個拓撲鄰接區域的多邊形進行標識。3）將所有多邊形按照面積從小到大排序，從面積較大的多邊形開始遍歷，將每一個拓撲鄰接區域中面積最大的多邊形（即外邊界圍成的無效多邊形N1N4N5N2N1）剔除。4）從面積較小的多邊形開始遍歷，根據每個多邊形的最小外界矩形范圍建立空間索引。5）依次處理每個多邊形，通過內點判定的方法尋找其是否被其它某個多邊形包含，可通過一些過濾操作來提高判定效率：根據2.3節的性質1可知，同屬于某個拓撲鄰接區域的多邊形之間不存在包含關系，則無需對相同拓撲鄰接區域的多邊形進行關系判定；由于在步驟4中使用多邊形最小外接矩形建立空間索引，因此可以根據多邊形最小外接矩形進行過濾操作，即最小外接矩形不存在包含關系的多邊形之間一定不存在包含關系。

3 分析與實驗

3.1 時間復雜度分析

假定n為輸入弧段數目，則弧段結點格網索引生成和方位角計算次數為2n，又因為在格網索引基礎上進行結點匹配，則匹配計算次數為k×n，即此過程時間復雜度為O（n）。多邊形搜索過程中因為每條弧段只經過左多邊形和右多邊形兩次搜索，則其時間復雜度也為O（n）。在傳統拓撲關系確定算法中，需要判定每個多邊形的內點與其它多邊形的包含關系，其時間復雜度為O（m2）（m為生成的簡單多邊形數目）；而改進算法可以將需要判定的簡單多邊形數目顯著減少為m0，時間復雜度為O（m20），且m0＜＜m，即算法整體時間復雜度為O（n＋m20）。

3.2 實驗結果分析

為了驗證該算法的有效性，使用C＋＋語言開發了原型系統，并使用多組不同規模的真實弧段數據進行對比測試，實驗環境為一臺主頻2.6 GHz的雙核處理器PC機，內存為2 GB。為了驗證本文提出的基于拓撲信息的多邊形生成算法（PG－TI）的高效性，與傳統算法和ArcGIS中的多邊形自動生成功能（Feature To Polygon）進行對比測試。

首先選取多組數據規模依次增大的弧段數據將PG－TI算法和傳統算法進行對比測試（表1）。由于兩個算法中多邊形生成數目均相等（且生成的多邊形形狀一致），即PG－TI算法保證了生成結果的正確性，因此不再將生成多邊形數目單獨列出。從表1可以看出，PG－TI算法在生成效率方面較傳統算法有了較大幅度的提升，且隨著測試弧段數目增加，提升效果更加顯著，即PG－TI算法對于大數據量下的多邊形數據自動生成具有較好的處理性能。

表1 多邊形自動生成測試結果對比Table 1 The result of polygon automatic generation comparison

為了進一步驗證PG－TI算法的有效性，將測試弧段數據轉換為Shape文件格式后在ArcGIS的Arc ToolBox模塊中使用Feature To Polygon功能進行對比驗證。表1中ArcGIS中的生成時間使用Arc ToolBox進度條中自動記錄的處理時間（精度為秒）。通過此組對比實驗可以看出，雖然ArcGIS的生成效率優于傳統算法，但PG－TI算法整體性能仍優于ArcGIS的多邊形自動生成功能，且弧段數據量較大時處理性能表現較好，對比結果如圖4所示。

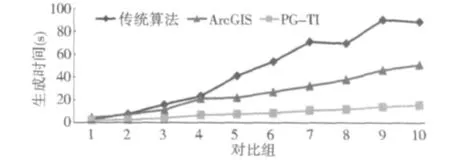
圖4 3種多邊形自動生成算法實驗結果比較Fig.4 Comparison of the experimental results of three methods of polygon automatic generations

4 結語

多邊形數據的自動生成是一個較為基礎與重要的數據處理操作，核心過程包括弧段鄰接關系確定、多邊形搜索、拓撲關系確定等步驟。本文在總結和分析已有算法基礎上，提出了一種基于拓撲信息的多邊形數據自動生成算法，通過多邊形搜索過程中生成的弧段左右多邊形信息生成拓撲鄰接區域，利用拓撲鄰接區域的優良性質使得拓撲關系確定過程的效率有了較大提升。對算法時間復雜度進行了分析，并使用多組真實弧段數據與傳統算法、ArcGIS的多邊形生成功能進行了對比實驗，證明本文算法處理性能優于傳統算法和ArcGIS的相應功能，且較適宜進行大規模弧段數據的多邊形自動生成處理。

［1］ 陳春，張樹文，徐桂芬.GIS中多邊形圖拓撲信息生成的數學基礎［J］.測繪學報，1996，25（4）：266－271.

［2］ 齊華.自動建立多邊形拓撲關系算法步驟的優化與改進［J］.測繪學報，1997，26（3）：255－260.

［3］ 閆浩文，楊維芳，陳全功，等.基于方位角計算的拓撲多邊形自動構建快速算法［J］.中國圖象圖形學報，2000，5A（7）：563－567.

［4］ 梁曉文，劉宗岐，陳宜金.基于夾角變化趨勢的多邊形自動搜索和生成算法［J］.中國圖象圖形學報，2005，10（6）：785－789.

［5］ 李大軍，劉波，趙寶貴，等.拓撲多邊形自動構建的一種改進算法［J］.計算機工程與應用，2005（16）：80－82.

［6］ 鄧敏，劉文寶，黃杏元，等.空間目標的拓撲關系及其GIS應用分析［J］.中國圖象圖形學報，2006，11（2）：1743－1749.

［7］ EGENHOFER M J，HERRING J.Categorizing binary topological relationships between regions，lines and points in geographic databases［R］.Oronoi：Technical report，Department of Surveying Engineering，University of Maine，Oronoi，ME，1991.

［8］ RANDELL D，CUI Z，COHN A.A spatial logical based on regions and connection［A］.Proceedings of 3rd International Conference on Knowledge Representation and Reasoning［C］.Morgan－Kaufman Publishers，1992.165－176.

［9］ LI Z，ZHAO R，CHEN J.An algebra model for spatial relations［A］.Proceedings of the 3rd ISPRS Workshop on Dynamic and Multi－dimensional GIS［C］.Bangkok，2001.170－177.

［10］ 吳建新，方裕，陳斌.拓撲空間關系描述理論研究現狀與發展［J］.地理與地理信息科學，2005，21（3）：1－4.

［11］ 齊華，劉文熙.建立結點上弧－弧拓撲關系的Qi算法［J］.測繪學報，1996，25（3）：233－235.

［12］ 高云瓊，徐建剛，唐文武.同一結點上弧－弧拓撲關系生成的新算法［J］.計算機應用研究，2002（4）：58－59.

Abstract：It is essential to GIS for automatic generation of polygon data，creation and maintenance of polygon topology information as many GIS operations are based on them.In this paper，the current polygon data automatic generation algorithms are summarized and analyzed，as well as polygon topology information generation algorithms with other scholars，a more efficient polygon data automatic generation algorithm based on topology information is proposed.Firstly，the core contents of the algorithm data structure are presented，describing the three core process including arc adjacency，polygon search and topology relationship determination.Secondly，the topology information creation by the polygon search process is described，which can accelerate the process of topology relationship determine.Finally，the algorithm time complexity analysis is presented，as well as the experimental verification.

Key words：GIS；polygon；topology information；contain relationship

A Polygon Data Automatic Generation Algorithm Based on Topology Information

LU Hao1，2，ZHONG Er－shun1，3，WANG Tian－bao1，2，WANG Shao－hua1，2
（1.Institute of Geographic Sciences and Natural Resources Research，CAS，Beijing 100101；2.Graduate University of the Chinese Academy of Sciences，Beijing 100039；3.Super Map Software Co.Ltd.，Beijing 100015，China）

P208

A

1672－0504（2012）04－0038－04

2012－01－09；

2012－03－06

盧浩（1984－），男，博士研究生，主要研究方向為GIS矢量核心算法。E－mail：luhaonihao2008＠163.com