土層缺陷錨桿錨固特性與參數影響分析

段建，言志信，郭銳劍，諶文武，劉子振,3，任志華

(1. 蘭州大學 西部災害與環境力學教育部重點實驗室，甘肅 蘭州，730000；

2. 蘭州大學 土木工程與力學學院，甘肅 蘭州，730000；

3. 臺州學院 建筑工程學院，浙江 臺州，318000)

巖土錨固技術具有巧妙結構、簡便工藝、經濟造價、獨特效果等突出優勢，在工程各領域獲得了廣泛應用[1]。目前，就完整錨桿錨固特性研究方面，眾多學者采用多種研究方法和手段取得了一系列研究成果，如Phillips等[2?6]采用相關理論來構建錨固體剪應力分布曲線函數；為了考慮巖土體彈塑性特性，Xiao等[7?9]分別建立巖土體彈塑性模型探討錨固體錨固機理；Yang等[10]采用分離式模型建立了基于混凝土基質的錨桿二界面分布函數理論；戰玉寶等[11?13]采用數值模擬技術分析錨固力學效應及影響因素；Delhomme等[14]通過試驗與數值模擬對比分析研究了基于混凝土基質的錨桿拉拔與蠕變特性；ZHAO等[15]分析了基于混凝土基質的缺陷錨桿拉拔特性。然而，在工程施工中，錨桿錨固質量影響因素繁多，常常使得錨固體難以飽滿，出現一些空腔缺陷，達不到設計要求，致使工程存在一定風險。而人們對有關缺陷錨桿錨固特性研究較少，因此，研究空腔對錨固系統的影響程度，為工程錨桿錨固質量后評價及修補決策提供理論支撐，均具有重要的理論和實踐意義。本文作者基于界面黏滑本構模型假定，構建錨固體位移、軸力、錨固體周邊剪應力微分表達式及土層缺陷錨桿錨固求解方法，探討土層缺陷錨桿荷載傳遞特性，分析缺陷錨固系統參數影響規律。

1 土層缺陷錨桿錨固力學模型

1.1 錨桿錨固體與周邊土體界面黏滑本構模型假定

為了考慮錨桿錨固體與周邊土體界面黏滑特性，界面剪應力?剪切位移關系可采用分段線性函數模式來表征，如圖1所示。第Ⅰ階段為彈性階段，錨桿錨固體?周邊土體協同承載變形，界面剪應力與剪切位移呈比例關系變化；一旦錨桿錨固體?周邊土體界面剪應力超過界面極限剪切強度，界面就會發生松動滑移，錨桿錨固體?周邊土體界面產生相對滑動，其剪切變形可任意發展，此時界面之間僅存在殘余剪切強度，如圖1中的第Ⅱ階段。

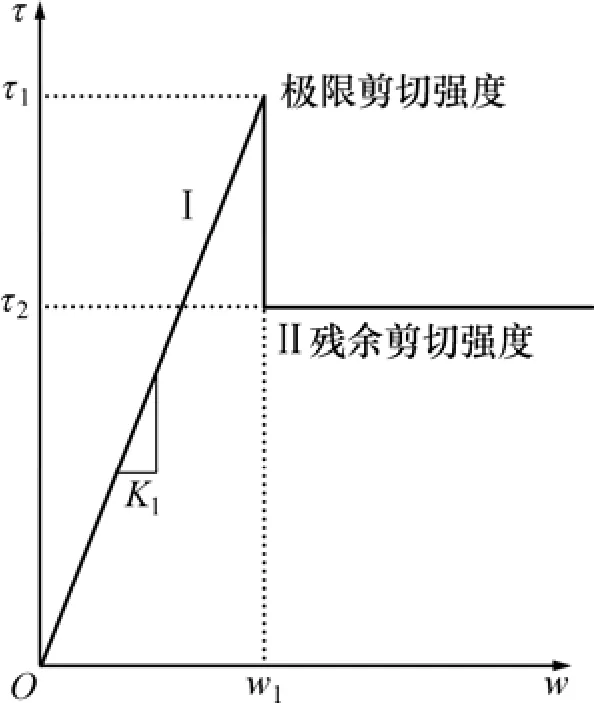
圖1 界面本構模型Fig.1 Constitutive model of interface

相應的錨桿錨固體?周邊土體界面黏滑本構關系數學表達式為：

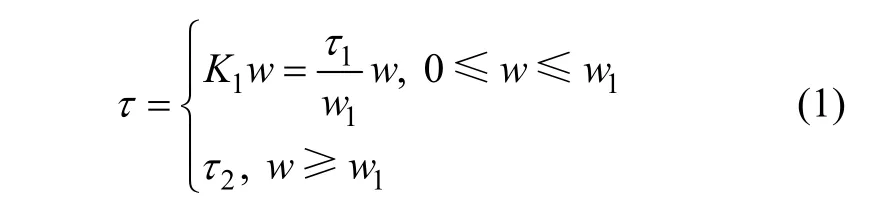
式中：τ為界面剪應力；K1為界面剛度系數；w為界面剪切位移；τ1為錨桿錨固段極限剪切強度；τ2為錨桿錨固段殘余剪切強度；w1為錨桿錨固段極限剪切強度所對應的剪切位移。

1.2 錨固力學模型的構建

土層錨桿錨固系統一般由錨桿(索)、錨固劑及周邊土體組成，可把錨桿(索)和錨固劑視為整體進行研究。因空腔缺陷的存在，土層缺陷錨桿錨固段被形成錨固?空腔交替組合的一種結構型式，共n段，其中偶數段為空腔，共(n?1)/2份，奇數段為錨固體，其對應(n+1)/2份，選取第i區段錨固段作為研究對象，如圖2所示，根據錨固體軸力Pi(z)與應力應變之間關系可得：

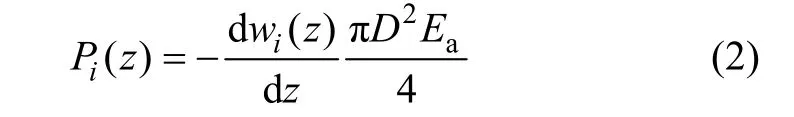
同時，由錨固體單元沿軸向方向力的平衡方程得：

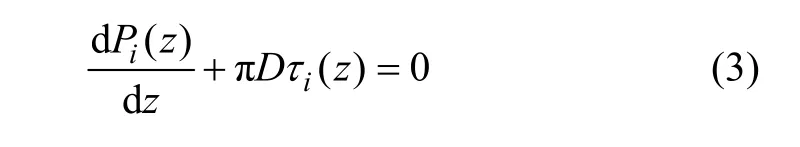
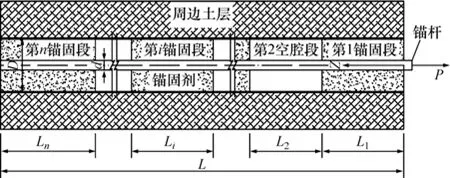
圖2 計算模型Fig.2 Compute model

聯立式(1)～(3)可獲得第i區段錨固體軸向位移微分方程為：

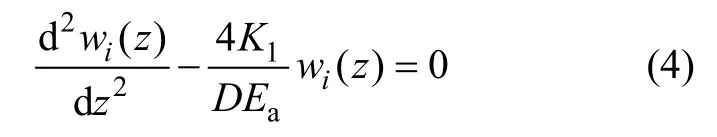
解為：

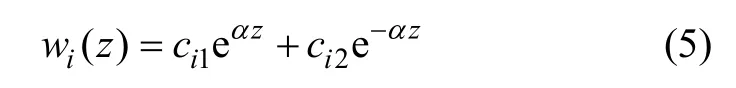
其中，ci1和ci2為待定常系數，可由該段邊界條件確定。

對式(5)求微分，分別代入式(1)和(2)可獲得第i段錨固體軸力及周邊剪應力分布函數為：

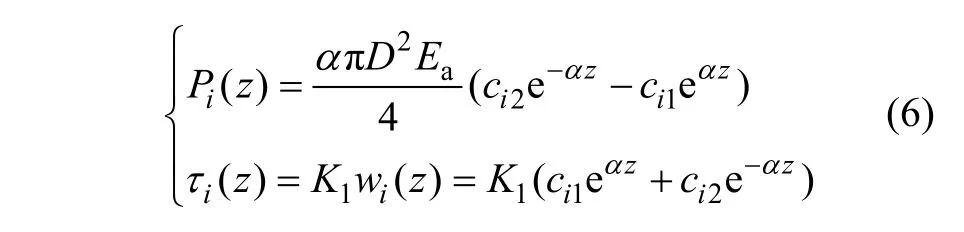
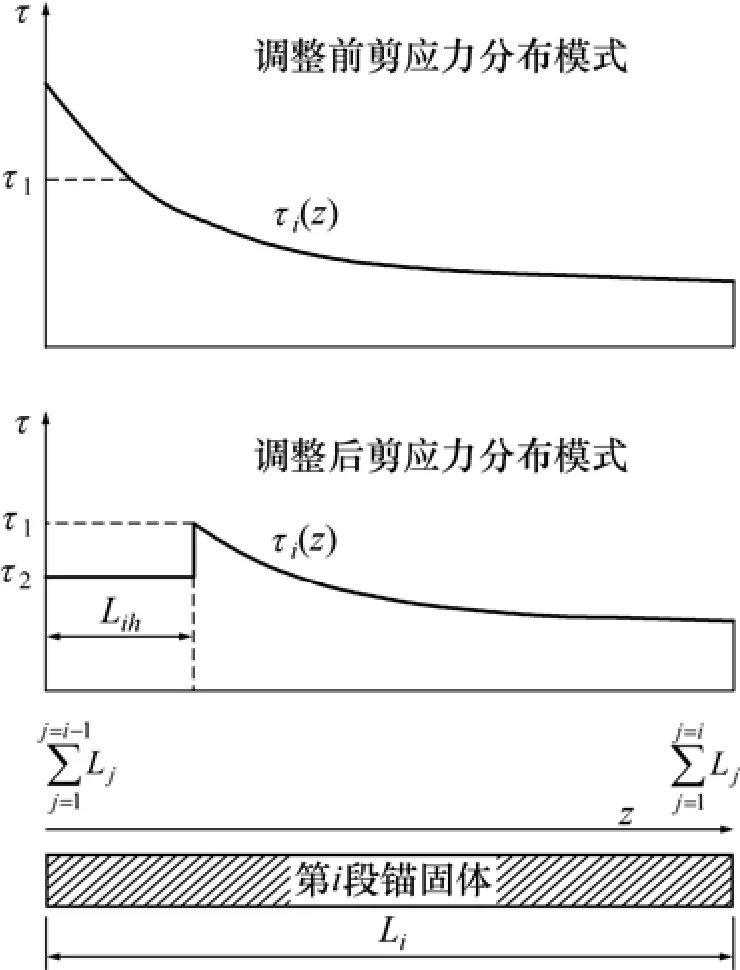
圖3 錨固體剪應力調整模式Fig.3 Adjusted model of anchorage shear stress

對應第i?1空腔段錨桿位移、軸力及剪應力分布函數，可依據相鄰第i錨固段力學特性及空腔特性確定：

1.3 缺陷錨桿錨固問題的求解步驟

依據上述所建錨桿錨固段以及空腔段力學模型與解析解，對某一具體的缺陷錨桿錨固工程問題，可按下列步驟獲得問題數值解。

第 1步：依據錨桿(索)設計長度及其空腔分布情況劃分研究區段n段，分別建立各錨固段錨固體位移、剪應力及軸力數學方程，基于第1，n錨固段端頭軸力邊界條件和各錨固段相鄰端頭位移及軸力連續條件(如式(8)所示)，即可確定各段待定常系數ci1，ci2，從而獲得各段錨固體位移、軸力及周邊剪應力分布數值彈性解。

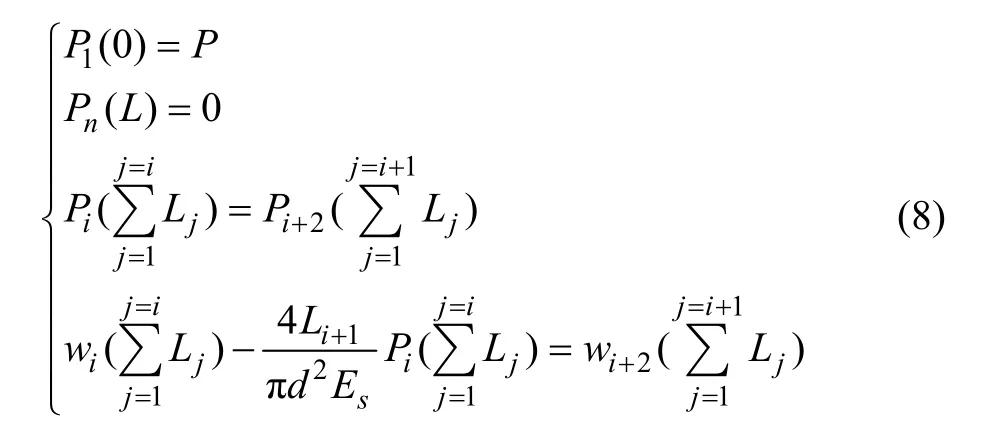
第 2步：依據錨桿錨固體剪應力衰減規律，τimax(z)=τ1max(z)=τ1(0)，通過界面力學參數τ1與τ1(0)的比較來判斷第1錨固段黏結?滑動狀態：當τ1(0)≤τ1，說明各錨固段界面均處于黏結狀態，剪應力不需調整分配，第1步所獲錨固段數值解即為問題解；同時，由式(7)即可確定各空腔段解析解；若τ1(0)＞τ1，即第1錨固段存在滑動區段，則對其按圖3滑動段剪應力調整模式進行修正，此時，邊界條件應修正為：

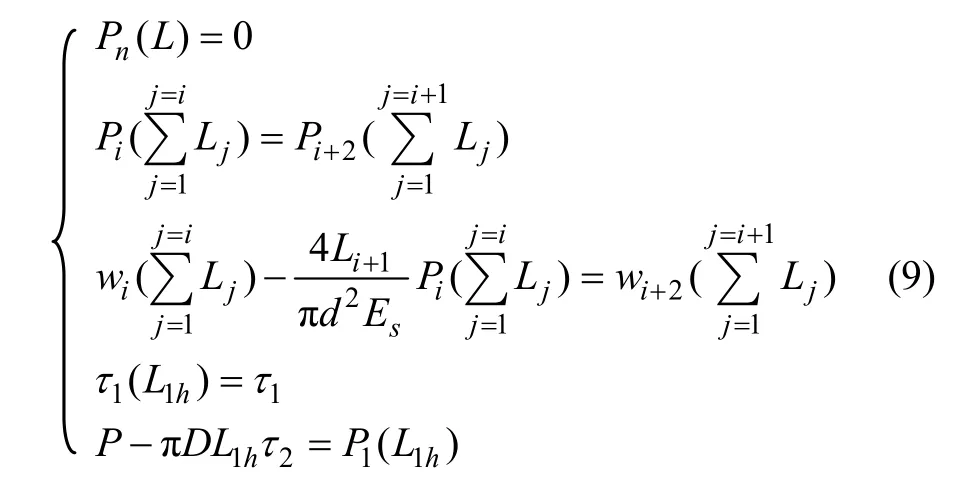
由式(9)和(7)分別可獲得各錨固段和空腔段調整后的數值解，而對于滑動段(0≤z≤L1h≤L1)，則可由式(10)確定：

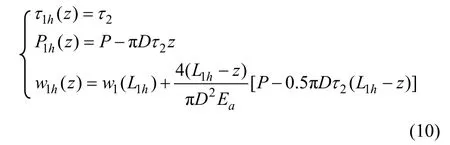
通過上述分析，土層缺陷錨桿錨固具體計算流程如圖4所示。

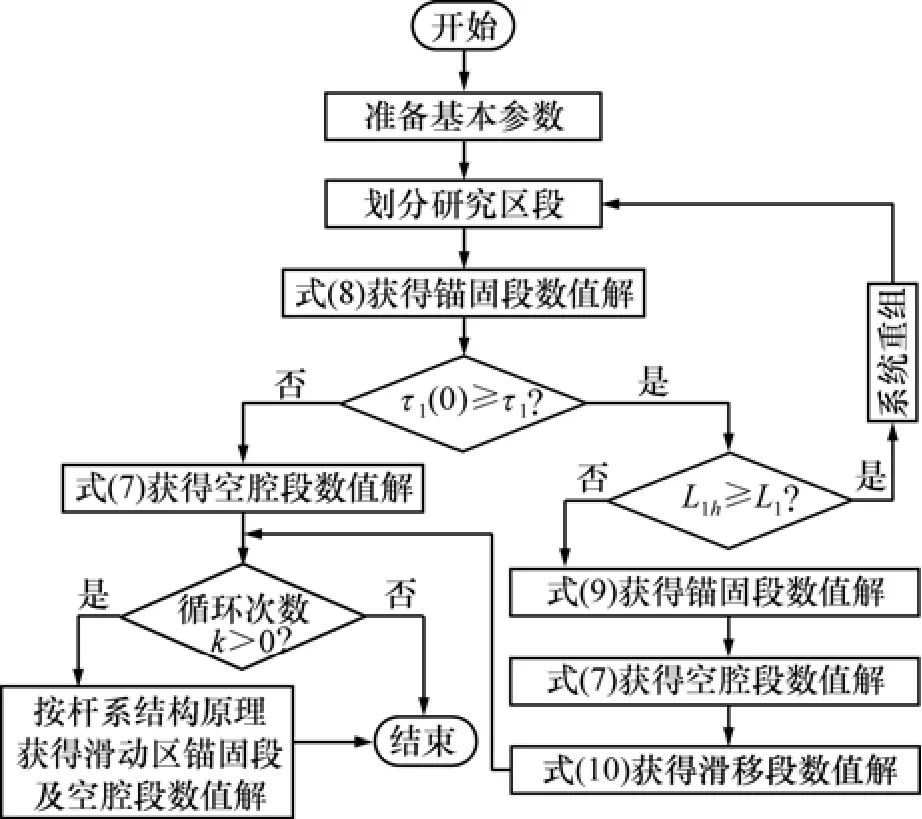
圖4 計算流程Fig.4 Computational process

1.4 理論模型的驗證

為了檢驗本文方法的合理性，工程選取湖南省株洲市天元區明峰銀座商住樓基礎工程，由鉆探揭露該場地地層巖性為：第4系全新統素填土與耕土、第4系上更新統粉質黏土與礫砂及粉砂、白堊系泥質粉砂巖。因場地地下水位較高，該工程采用錨桿基礎抗浮，共施工了抗浮錨桿 817根，采用φ28螺紋鋼(三級鋼)制作，孔徑為130 mm，錨固劑采用M30水泥砂漿。對其中41根工程錨桿進行了抗拔試驗(未做錨固體應力測試)，為了驗證本文方法的合理性，選取其中第420號錨桿荷載?位移檢測數據進行對比分析。該錨桿全長為6.5 m，錨固質量完整，全長穿越圓礫碎石土(未穿透)，根據其勘察成果，同時綜合參考該地區同類土測試資料、巖土力學參數手冊及相關工程經驗，本工程地層物理力學參數見表1。

設計錨桿抗拔承載力特征值為128 kN，抗拔試驗最大荷載根據規范及設計要求確定為 190 kN，采用QFZ100-20型張拉千斤頂與手搖高壓油泵對錨桿進行施加拉拔力，試驗采用分級加荷載法，前3級荷載按試驗荷載的20%施加，以后按10%施加，分別對應荷載為38，76，114，133，152，171和190 kN，每級穩定后加下一級荷載，并記錄對應的位移。

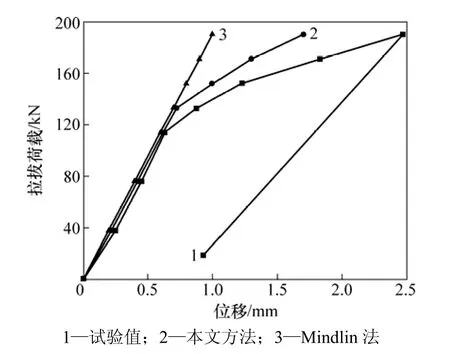
圖5 420號錨桿載荷?位移曲線Fig.5 Load?displacement curve of No.420 anchor

錨桿拉拔試驗獲得的錨桿荷載-位移曲線及按本文方法及Mindlin法[3]計算的理論荷載?位移曲線如圖5所示。從圖5可見：當拉拔荷載比較小時，曲線均呈線性變化；隨著荷載的增大，因Mindlin法是基于彈性理論原理構建的，荷載與位移間始終保持線性關系變化，而本文方法考慮了界面的黏滑特性，約在P=133 kN位置曲線開始向X位移軸偏轉，變形速率增大，界面發生松動，與 Mindlin法相比，其結果更接近于實際。同時說明，從工程安全角度考慮，錨桿抗拔承載力特征值取128 kN是安全合理的；按照相關規范，工程錨桿拉拔至最大試驗荷載190 kN，然后卸載至19 kN，可將試驗卸載曲線延伸至X軸，發現錨桿變形并未歸 0，產生了一定的塑性變形，這與本文方法計算結果一致。

2 土層缺陷錨桿錨固特性的參數影響分析

為了充分了解土層缺陷錨桿的荷載傳遞特性，基于一土層單空腔缺陷錨桿算例和本文方法分別從空腔大小、空腔位置以及拉拔荷載3方面開展缺陷錨桿錨固特性參數影響分析。算例基本資料如下：錨桿孔孔徑D為110 mm，采用φ32螺紋鋼筋，設計長度L=6 m，Es=200 GPa；錨固劑采用水泥砂漿，Em=20 GPa；周邊土體力學參數K1=0.6 GPa/m，τ1=0.5 MPa，τ2=0.2 MPa；錨固體全長僅存在一處空腔，具體幾何特征由其研究內容決定。

2.1 空腔尺寸的影響

假定空腔末端位置不變，z=4 m，拉拔荷載P=150 kN，設計4種缺陷長度方案：L2=0 m，L2=1 m，L2=2 m，L2=3 m，圖6所示為空腔尺寸對錨桿錨固特性的影響結果。在相同荷載作用下，缺陷錨桿表現出與完整錨桿不一樣的錨固特征，空腔的存在使得錨固段同一截面處剪切位移和剪應力均增大，空腔前段錨固段軸力減小，而后段則增大，總體上，空腔對缺陷錨桿前段錨固段錨固特性影響較大，而后段不是很明顯；空腔段錨桿軸力及剪應力分布均為一水平平臺，而剪切位移則為一下降直線形式，表現出明顯的桿系結構受力特征。

同時，由圖6還可得知：空腔尺寸對缺陷錨桿錨固特性影響也很大。隨著空腔長度的增大，錨固段同一截面處剪切位移與剪應力均增大，軸力缺陷前段錨固段減小而后段增大；對應空腔段剪切位移下降幅度越大，軸力平臺值也越大，而剪應力始終保持“0”水平平臺特性。

2.2 空腔位置的影響

假定錨桿空腔缺陷長度L2=1 m，其他物理力學參數不變，考慮 1≤z≤2(位置 1)，2≤z≤3(位置 2)，3≤z≤4(位置3)3種空腔位置方案，分析P=150 kN作用下缺陷位置對錨桿錨固特性的影響，計算結果見圖7。由圖7可知：空腔位置越靠近拉拔頂端，前段錨固段同一位置處剪切位移和剪應力均越大，相應錨桿軸力下降幅度越大，而后段錨固段剪切位移、軸力及剪應力變化甚少，受影響程度小；對于錨桿空腔段，缺陷位置越靠近拉拔端，剪切位移斜率越小，軸力越大，剪應力則始終保持“0”水平平臺特征。

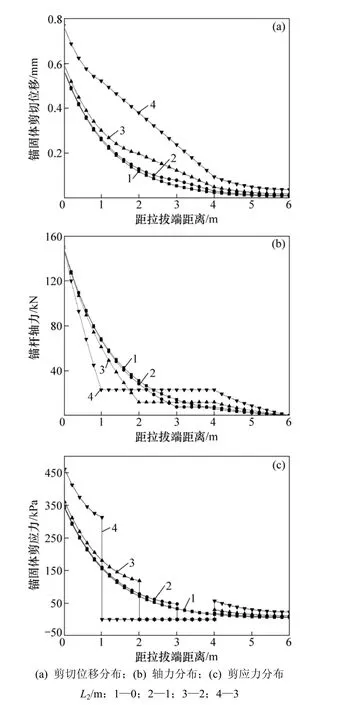
圖6 不同空腔尺寸下缺陷錨桿錨固特征Fig.6 Anchorage characteristics of imperfect anchor under different imperfect dimensions

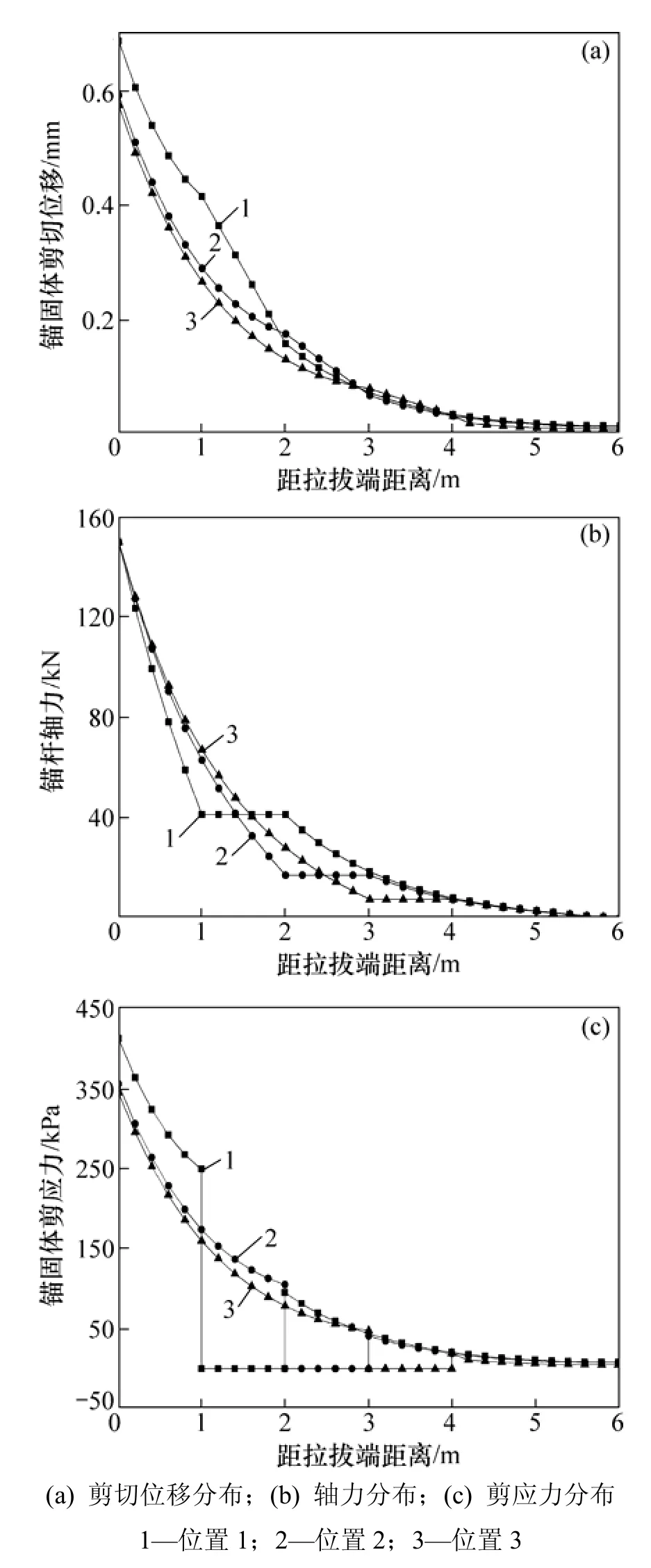
圖7 不同空腔位置條件下缺陷錨桿錨固特征Fig.7 Anchorage characteristics of imperfect anchor under different imperfect locations

2.3 拉拔荷載的影響

假定錨桿空腔缺陷位于 3≤z≤4區段，其長度L2=1 m。根據上述計算方法，考察3種拉拔荷載P=100，200，240 kN作用下缺陷錨桿錨固段剪切位移、軸力及周邊剪應力分布特征，如圖8所示。從圖8可見：當荷載較小時，隨距錨固頂端距離的增大，錨固段剪切位移、軸力及剪應力均在衰減；同時，隨著拉拔荷載的增大，錨固段同一位置處剪切位移、軸力及剪應力均在增加；當P=240 kN時，錨桿孔口處剪應力τ1(0)=0.551 MPa，已超過界面抗剪強度，剪應力需重新調整分配，通過計算獲得錨桿松動滑移長度L1h=0.341 m，調整后相應滑動段上的剪應力轉化為界面殘余剪切強度，后續黏結段剪切位移、軸力及剪應力均比調整前有所上升，說明滑移松動后荷載進一步往錨桿里端傳遞，加劇里端錨固體損傷劣化；此外，隨著荷載的增大，空腔段剪切位移下降直線對應斜率越小，剪切位移急劇下降，軸力及剪應力分布均為一水平平臺，其中荷載越大，軸力也增大，而剪應力始終保持“0”水平平臺特征。

圖8 不同荷載作用下缺陷錨桿錨固特征Fig.8 Anchorage characteristics of imperfect anchor under different loading

3 結論

(1) 依據界面黏滑本構模型假定，建立了錨桿錨固力學微分方程及其解析解，給出了土層缺陷錨桿錨固迭代計算方法與求解步驟，并結合已有的工程實例驗證了本文方法的可行性。

(2) 缺陷錨桿具有與完整錨桿不一樣的錨固特征，其剪切位移、軸力與剪應力分布函數均由連續多段函數形式組成，其中空腔段錨桿軸力及剪應力分布均具有水平平臺特性。

(3) 界面黏滑特性導致剪應力重新調整分配，調整后錨桿錨固段剪切位移、軸力及剪應力均有所上升，荷載進一步往里端傳遞，加劇里端錨固段的損傷劣化。

(4) 空腔的存在對缺陷錨桿前段錨固段影響較大，而后段則影響較小。

[1] 程良奎. 巖土錨固的現狀與發展[J]. 土木工程學報. 2001,34(3): 7?16.CHENG Liang-kui. Present status and development of ground anchorages[J]. China Civil Engineering Journal, 2001, 34(3):7?16.

[2] Phillips S H E. Factors affecting the design of anchorages in rock[R]. London: Cementation Research Ltd, 1970: 1?10.

[3] 尤春安. 全長粘結式錨桿的受力分析[J]. 巖石力學與工程學報, 2000, 19(3): 339?341.YOU Chun-an. Mechanical analysis on wholly grouted anchor[J].Chinese Journal of Rock Mechanics and Engineering, 2000,19(3): 339?341.

[4] 尤春安, 戰玉寶. 預應力錨索錨固段應力分布規律及分析[J].巖石力學與工程學報, 2005, 24(6): 925?928.YOU Chun-an, ZHAN Yu-bao. Distributing characters and analysis of stresses in prestressed cable[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(6): 925?928.

[5] 蔣忠信. 拉力型錨索錨固段剪應力分布的高斯曲線模式[J].巖土工程學報, 2001, 23(6): 696?699.JIANG Zhong-xin. A gauss curve model on shear stress along anchoring section of anchoring rope of extensional force type[J].Chinese Journal of Geotechnical Engineering, 2001, 23(6):696?699.

[6] 張季如, 唐保付. 錨桿荷載傳遞機理分析的雙曲函數模型[J].巖土工程學報, 2002, 24(2): 183?192.ZHANG Ji-ru, TANG Bao-fu. Hyperbolic function model to analyze load transfer mechanism on bolts[J]. Chinese Journal of Geotechnical Engineering, 2002, 24(2): 183?192.

[7] XIAO Shu-jun, CHEN Chang-fu. Mechanical mechanism analysis of tension type anchor based on shear displacement method[J]. Journal of Central South University of Technology,2008(15): 106?111.

[8] 何思明, 李新坡. 預應力錨桿作用機制研究[J]. 巖石力學與工程學報, 2006, 25(9): 1876?1880.HE Si-ming, LI Xin-po. Study on mechanism of prestressed anchor bolt[J]. Chinese Journal of Rock Mechanics and Engineering, 2006, 25(9): 1876?1880.

[9] 何思明, 田金昌, 周建庭. 膠結式預應力錨索錨固段荷載傳遞特性研究[J]. 巖石力學與工程學報, 2006, 25(1): 117?121.HE Si-ming, TIAN Jin-chang, ZHOU Jian-ting. Study on load transfer of bond prestressed anchor rope[J]. Chinese Journal of Rock Mechanics and Engineering, 2006, 25(1): 117?121.

[10] Yang S T, Wu Z M, Hu X Z, et al. Theoretical analysis on pullout of anchor from anchor-mortar-concrete anchorage system[J].Eng Fract Mech, 2008, 75(5): 961?985.

[11] 戰玉寶, 畢宣可, 尤春安. 預應力錨索錨固段應力分布影響因素分析[J]. 土木工程學報, 2007, 40(6): 49?53.ZHAN Yu-bao, BI Xuan-ke, YOU Chun-an. Analysis of factors influencing the stress distribution in prestressed cables[J]. China Civil Engineering Journal, 2007, 40(6): 49?53.

[12] 江文武, 徐國元, 馬長年. FLAC-3D 的錨桿拉拔數值模擬試驗[J]. 哈爾濱工業大學學報, 2009, 41(10): 129?133.JIANG Wen-wu, XU Guo-yuan, MA Chang-nian. Numerical simulation on pull-tests of a cable by FLAC-3D[J]. Journal of Harbin Institute of Technology, 2009, 41(10): 129?133.

[13] 龐有師, 劉漢龍, 陳育民. 可回收式錨桿拉拔試驗的數值模擬與影響因素分析[J]. 解放軍理工大學學報: 自然科學版,2009, 10(2): 170?174.PANG You-shi, LIU Han-long, CHEN Yu-min. Numerical simulation of removable anchor pullout test and influence factors[J]. Journal of PLA University of Science and Technology:Natural Science Edition, 2009, 10(2): 170?174.

[14] Delhomme F, Debicki G. Numerical modeling of anchor bolts under pullout and relaxation tests[J]. Constr Build Mater, 2010,24(7): 1232?1238.

[15] ZHAO Yi-ming, YANG Mi-jia. Pull-out behavior of an imperfectly bonded anchor system[J]. International Journal of Rock Mechanics & Mining Sciences. 2011 (48): 469?475.