AutoCAD中判斷折線自相交的一種快速算法

周建康，冷泠，王瑞青

(鄭州市規劃勘測設計研究院，河南鄭州 450052)

1 引言

折線自相交是地理信息系統空間線性數據處理中的一個比較重要、常見和復雜的問題，

在地圖綜合、空間分析、CAD數據向GIS數據轉換等諸多領域有著廣泛的應用。例如，空間分析中常見的多邊形緩沖區分析，既要求參與分析的多邊形不能存在自相交現象，又要求生成的緩沖區多邊形不能存在自相交情況。但是，由于空間數據的復雜性與多樣性，在實際數據生產與應用中，不可避免地會產生折線自相交。因此，設計一種快速判斷并定位折線自相交的算法是地理信息系統設計中需要解決的問題。國內外一些學者對此問題進行了相關探討和研究，也取得了一些成果［1～3］，這些算法作為通用算法可以初步解決折線自相交的判斷問題。但在應用到數據生產中時，由于沒有結合具體的系統平臺特點，不僅在算法上無法做到最優，同時在面對復雜和海量的空間數據時效率低下，無法滿足生產需求。

AutoCAD作為CAD默認行業標準，在我國很多行業有著廣泛應用。一方面在城市規劃、測繪等領域，各單位存在大量的DWG數據及許多基于AutoCAD的應用系統;另一方面，在基礎地理信息數據的采集中，AutoCAD或基于AutoCAD的數據采集平臺被廣泛使用，AutoCAD支持下的地形圖數據和其他行業數據成為城市基礎地理信息系統和專業地理信息系統建設的主要數據源。因此，在AutoCAD中解決折線自相交的快速判斷，可以有效保證數據的質量，為數據的GIS應用奠定基礎。但從目前現狀看，包括很多商業軟件在內都沒有很好地解決或者避開該問題。

2 折線自相交判斷的一般算法

自相交判斷的一般算法是基于折線自相交問題的定義提出的。

2.1 折線自相交問題定義

設有折線 l={p1，p2，…，pn}，(i=1，2，…，n)，pi是折線上順次連接線段的端點。若除了相鄰線段間的連接端點p1，p2，…，pn外，折線上的線段還存在其他交點，則定義此折線為自相交折線。

2.2 判斷折線自相交的一般算法

判斷折線自相交一般都是采用以下算法或者基于此算法演變而來。

對于折線l上的線段，按照其連接順序分解為多條兩點組成的線段，兩兩判斷這些線段是否相交，根據交點情況和自相交的定義來判斷折線l是否自相交，如果自相交則求出自相交交點，這就將問題轉化為兩線段的相交問題。兩線段的相交判斷采用以下方法:

設有兩條線段 K1(p1，p2)、K2(p3，p4)，欲求其交點，需要先判斷它們是否相交，為此設:

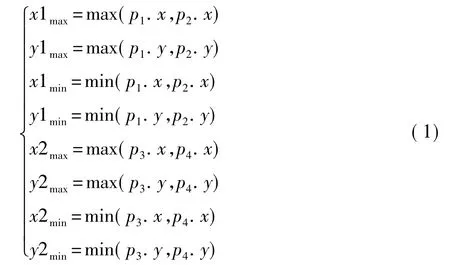
若 x1max＜x2min或 y1max＜y2min或 x1min＞x2max或 y1min＞y2max則K1、K2不相交;否則，需要進一步判斷，為此設:

p1p2的直線方程為 f(x，y)=dx(y－p1.y)－dy(xp1.x)=0。凡在 p1p2上的點必滿足 dx(y－p1.y)－dy(x－ p1.x)=0，而其他點使 dx(y－p1.y)－dy(x－p1.x)≠0，且在直線兩側的半平面內的點使上式異號。因此，判斷p3、p4在K1不同側的充分必要條件是:f(p3.x，p3.y)*f(p4.x，p4.y)≤0。若兩個線段的端點都在對方的不同側，則此兩線段相交。

該算法的優點是簡單、直觀;缺點是計算煩瑣、運算量大，在時間上不是最優。

3 基于AutoCAD的折線自相交快速判斷算法

AutoCAD中的折線是指其對象類型中的多段線。多段線的組成包括直線段或圓弧段，采用上文的一般算法不僅需要計算線段的交點，還可能需要圓弧的交點，運算量相當大，尤其是當數據量大時，運算時間上是無法忍受的。因此，本文在分析AutoCAD數據結構和Offset(偏移)方法的基礎上，利用其自身處理原則，快速地實現了多段線自相交的判斷和相交點定位。

3.1 AutoCAD的Offset方法分析和折線自相交判斷算法依據

Offset方法是AutoCAD提供的一種平行線創建方法。平行線創建算法也是計算幾何中研究比較多的一個算法，尤其是在處理平行線創建過程中產生的自相交情況。AutoCAD只提供了Offset操作和該操作的二次開發接口，沒有提供該方法的核心算法說明，經數據多種情況操作試驗分析，得出了其處理的過程和基本原則。

第1步，判斷多段線的方向。AutoCAD中的多段線有順時針方向和逆時針方向之分，對于順時針方向，Offset方法的距離值為正值時為向內偏移，距離值為負值時為向外偏移;對于逆時針時剛好相反。這里可以簡單理解為創建平行線時根據偏移距離的正負，Offset方法會根據預定義規則往多線段前進方向的同側(左側或右側)偏移創建平行線(圖1，多段線L的方向如圖所示，偏移距離為+10 mm)。

第2步，將多段線分解成相鄰兩點構成的線段，根據多段線的方向，對每段線段分別創建平行線(圖1中虛線，這里所有平行線一定都在L前進方向的右側)。

第3步，根據原始多段線的線段順序，對生成的每段平行線按順序進行連接或裁剪處理，生成最終平行線。具體連接或裁剪的原則為:連接或裁剪時按照原始多段線的前進順序，對平行線段的首尾進行處理。相鄰的平行線段如果相交，則裁剪刪除掉相交點外多余的部分(圖2中A點虛線部分)，如果不相交，則延長至相交連接(圖2中B、C、D虛線部分)，如果延長不相交(自相交或偏移距離過大)，則該段無法創建平行線(圖4中BC段與CD段重疊自相交，創建的平行線段不相交，則在此段無法創建平行線，此段之前的平行線段也會被舍棄，最終只能生成平行線ab);如果平行線與原始多段線相交，則從臨近原始多段線一側偏移距離處裁剪刪除(圖2中E、F點距離L線10 mm)。

第4步，最終生成平行線。根據處理原則可以分析出，“葉形”自相交(除自相交點外自相交部分都不在線上)Offset后會產生多條平行線(如圖3，產生2條);“回頭線”自相交(自相交部分完全與線本身重合)只產生一條平行線，但平行線節點數一定少于原始多段線(如圖4平行線ab)。

需要注意:偏移距離不能過大，過大可能會導致平行線無法創建。

圖1 分段創建平行線段 圖2 處理平行線段為平行線 圖3 Offset方法最終結果圖

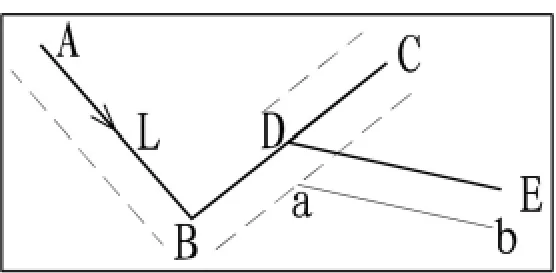
圖4 “回頭線”自相交Offset圖

經過以上分析，我們可以得出結論:在盡可能小的偏移距離(最好產生平行線直接與多段線近似重疊效果，可以直接避免偏移距離過大造成的平行線創建失敗，同時可以方便自相交點的定位)下，Offset方法只有在自相交的情況下，創建平行線數量才會大于一條或者只有一條平行線但平行線的節點數小于原多段線，且多段線自相交點一定位于平行線的首尾處(偏移距離小，平行線的首尾點基本上與自相交點重合)。

3.2 基于AutoCAD的Offset方法的算法

Offset方法創建平行線可以用:

來表示，其中A表示創建的平行線集合，L(t)為初始多段線，d表示平行線偏移距離，n(t)是多段線在參數t處的單位方向向量。

基于上文中的結論，結合式(3)，AutoCAD中多段線自相交快速判斷算法可以描述為:

第1步:獲取需要判斷處理的多段線，賦值為對象變量L;

第2步:對L進行Offset操作，偏移距離絕對值d盡量等于0但一定大于0(如0.00001)，獲得平行線集合A;

第3步:獲取集合A的數量A.count;若A.count=1，則比較平行線A(0)的節點數與L的節點數，如果A(0).pointCount=L.pointCount，可判斷 L 線無自相交情況，如果 A(0).pointCount＜L.pointCount，即可判斷 L線存在自相交，且自相交點位置位于A(0)的首尾處;若A.count＞1，則可判斷L線存在自相交，且自相交點位置位于A集合中所有線對象的首尾點處。

需要注意:當自相交線的平行線集合A中線對象的首尾點位于多段線L的首尾點時，該點可能不是自相交點，但為加快運算速度，不再進行判斷，直接標記該點后人工可以快速判斷和處理。

第4步:返回自相交和自相交點位置信息，結束運算。

算法流程圖如圖5所示。

4 結論

AutoCAD中基于Offset方法的折線自相交快速判斷算法，無論從算法的空間復雜度上還是時間復雜度上都較一般常規算法有了特別明顯地改善，提高了AutoCAD中基礎地理信息數據的折線自相交問題的處理效率，解決了一直以來AutoCAD中多段線自相交的快速自動判斷和定位問題。采用該算法基于VBA對鄭州市規劃控制六線50多萬條多段線數據的自相交質量檢測應用表明，該算法具有實現簡單、運算速度快、穩定性好、完善實用等特點。

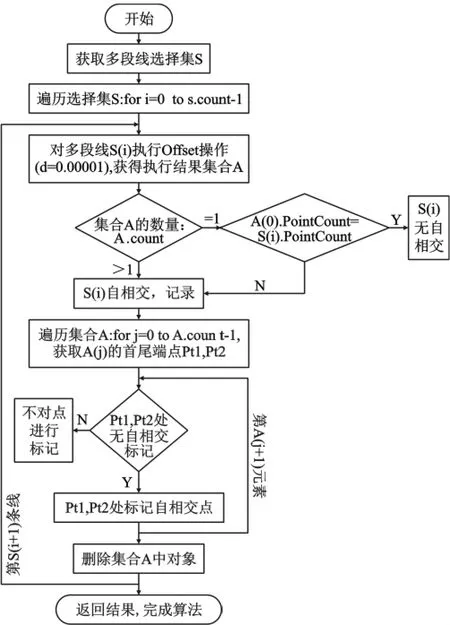
圖5 算法流程圖

［1］Mark de Berg，Marc van Kreveld，Mark Overmars，et al.Computational Geometry:Algorithm and Applications［M］.New York:Springer，1993

［2］楊維芳.判斷折線自相交的快速算法［J］.蘭州鐵道學院學報(自然科學版)，2002，21(3):76 ～78

［3］周培德.計算幾何［M］.北京:清華大學出版社，2000

［4］曾洪飛，張帆，盧擇臨.AutoCAD VBA＆VB.NET開發［M］.北京:中國電力出版社，2008

［5］郭仁忠.空間分析［M］.武漢:武漢測繪科技大學出版社，1997

［6］吳千里，馬小龍.面向城市規劃信息化的GIS與CAD集成技術探討［J］.測繪通報，2010(2):52～55