公交發車頻率與交叉口信控參數的協調關系研究＊

柏海艦 董瑞娟 李文權 張衛華

（合肥工業大學交通運輸工程學院1） 合肥 230009） （東南大學交通學院2） 南京 210096）

0 引 言

公交優先的理念已被大多數城市廣為接受，優先不僅僅需要宏觀政策上的引導，也需要微觀技術上的支撐.公交車輛在道路上的優先主要體現在路權優先和信號優先2種形式，本文研究了上游交叉口信號控制參數與公交站點停靠線路發車頻率的協調關系，充分體現了公交在微觀上的優先.國內外關于交叉口內公交信號優先［1－3］的研究內容較多，但交叉口信控參數與下游公交站點的關系研究極少.有些學者研究了信控條件下的交通間斷流模型，但對間斷流條件下公交車流特性研究很少.公交站點由于公交車流的短時集中而擁堵的現象屢見不鮮，紅燈閑，綠燈堵，嚴重降低公交站點的服務水平，影響相鄰車道的車輛正常運行.因此，研究站點線路發車頻率與上游交叉口信控參數的協調關系及其優化方法對緩解公交站點處的擁堵有著重要的作用.本文從間斷公交車流形成機理及其特征參數的研究出發，建立間斷公交車流特征參數與交叉口信控參數的關系；分析下游公交站點的運行特征，推導間斷公交車流條件下，下游公交站點通行能力需滿足的公式，從而構建公交站點停靠線路發車頻率與上游交叉口信控參數之間的協調關系式.通過實例計算，對二者的關系模型進行求解，驗證模型及求解方法的合理性.

1 間斷公交車流的特性分析

如圖1所示，交叉口的車流運行示意圖中，交叉口為4相位信號控制，可假設西進口直行車道的通行能力為Qs，進口直行車道的車流量為qs，交叉口西進口的綠燈時間為tg，信號周期為T.由西進口直行并停靠下游站點的公交車流的總到達率為λs＝ ∑λi.式中：λi＝60／Ni，Ni為第i條線路的發車頻率，輛／min.

由圖1可見，交叉口下游的交通流由于受信號影響，形成間斷交通流.同理，公交車流作為交通流的一部分也形成間斷流.因此可根據車流波動理論計算間斷公交車流中公交車輛的平均到達率.假設直行綠燈時間內直行車道通過車輛數與通行能力相同，則在直行綠燈時間內，通過的公交車輛數m為

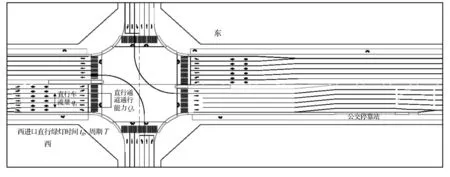
圖1 公交站點與上游交叉口關系示意圖

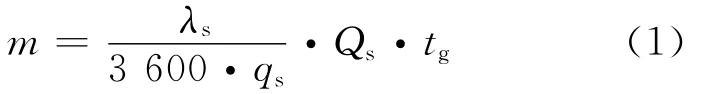
設間斷公交車流中連續段的公交車輛到達率為λ，則λ和m滿足

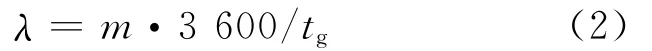
將式（1）代入式（2）得

通常左轉車流流量相對較小，且其中的公交車流量也較少，本文暫不考慮南北相位公交車流所形成的短間斷流，只以直行間斷流作為研究對象.紅燈閑，綠燈堵的現象主要是因為短時間內有多輛公交車輛到達站點，超過站點的泊位數而導致排隊擁堵.因此分析一段車流中，公交車輛的到達特性顯得尤為重要.從整條道路來看，交通流呈現間斷流特征；從間斷流本身內部特性來看，其每一段又可以看作有限總體的簡單流，且符合泊松分布規律.

2 間斷流條件下站點－上游交叉口系統分析

2.1 站點系統運行特性

如圖2所示，假設停靠站點有4個泊位，公交車輛減速進站時間為tj，站內平均上下客服務時間為td，公交車輛最小安全反應車頭時距為ta，則1號車開始進站到5號車開始進站的時間間隔為tj＋td·（g／c）＋k·ta.g，T 分別為站點下游交叉口的綠燈時間和周期；B為站點的物理設施最大通過能力［4－7］.則有

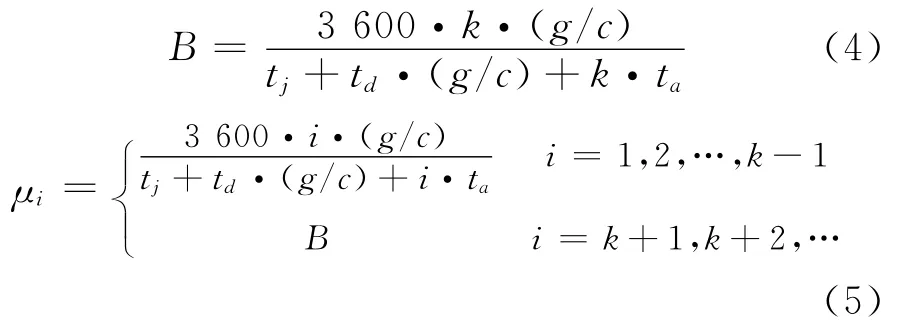
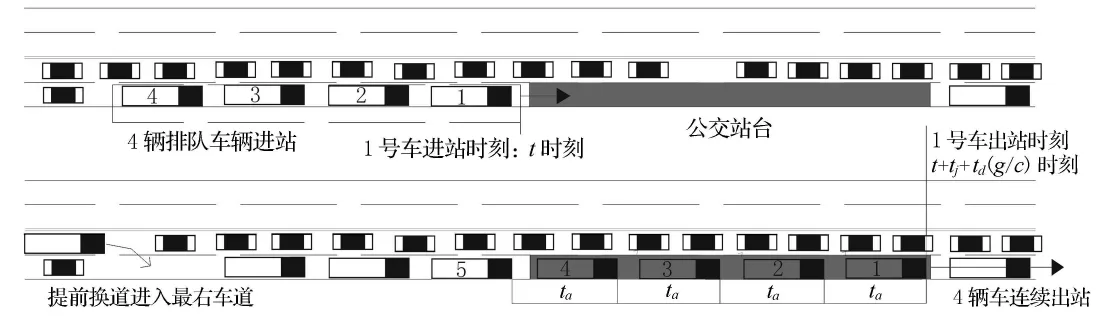
圖2 公交車進出站點運行示意圖

2.2 站點－上游交叉口生滅系統特性

從前文分析可以看出，由于交叉口信控的影響，到達公交站點的公交車流呈現間斷流，且每段車流符合泊松分布，符合生滅系統特征，且是有限輸入總體的生滅系統，因此可采用生滅過程進行分析.如圖3所示，其中λ表示間斷流公交車輛中連續段的公交車輛到達率，即生滅系統的輸入率；μi為站點的輸出率；si為系統中有i輛公交車的狀態.

圖3 有限輸入總體的生滅系統示意圖

根據生滅系統［8－9］的數學公式得出路內站點生滅狀態方程組.

對于站點系統中沒有車輛的狀態即i＝0時，其狀態方程為

對于站點系統中有i輛公交車的狀態其狀態方程為

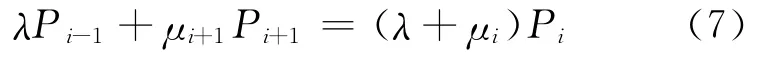
式中：Pi為站點同時有i輛車到達的概率，i＝0，1，2，….

根據式（6）、式（7）遞推可得

根據式（8）～（10）可通過數學歸納法推導證明k個泊位的站臺其P0的計算式為

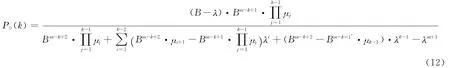
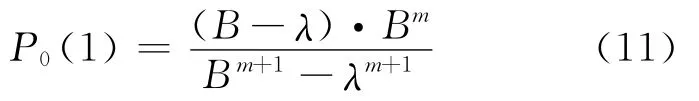
式中：P0（k）為k個泊位數的站點有0輛車到達的概率，即有k個泊位數站點的P0值.

根據停靠站泊位數不同，聯立公式（8）、（9）、（11）、（12）可解得不同泊位數的站點計數間隔時間內公交車輛到達的概率為

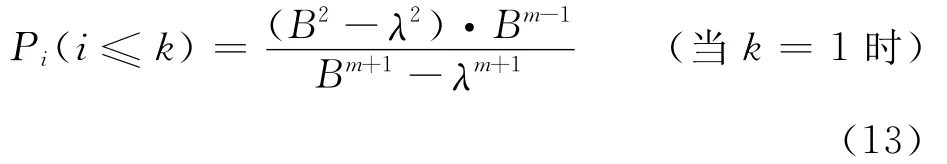
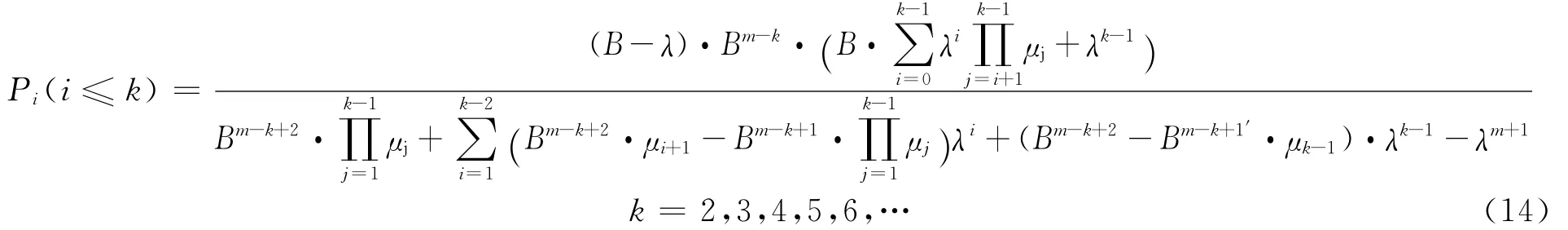
2.3 公交站點停靠線路發車頻率與上游信號控制的關系［10－13］

根據左轉車流量大小，交叉口的信號控制形式可分為設左轉專用相位和不設左轉專用相位.設左轉專用相位的信控交叉口其左轉車流量較大，左轉車流形成的間斷流也需要考慮.但從信號相位圖可以看到，可以通過直－左－左－直或左－直－直－左的相序排列將左轉間斷流與直行間斷流分開.一般情況下直行間斷流比左轉間斷流長，對下游的影響更大，應作為主要研究對象.而對于不設左轉相位的交叉口，其左轉車流量小，在不影響分析合理性的情況下可不作考慮.因此，采用4相位的信控形式下直行間斷流為例建立二者的關系方程.

考慮到實際車流運行的隨機性，即使正常車流，也可能出現站點偶爾排隊，研究的重點應該是避免經常性排隊而不是偶發性排隊.因此采用車輛進站排隊的概率作為間接指標來評價站點的擁堵狀況，間斷流排隊概率的計算應分為2個部分：（1）間斷流中分段車流含有k輛或k輛以上公交車的概率β；（2）含有k輛或k輛以上公交車的分段車流在站點出現排隊的概率α，限于篇幅論文未討論α，β的取值，可根據不同城市的實際情況取定，這里暫取為0.3，據此可得如下方程

聯立式（2），（3），（16），（17）構成了λ，λs，m，Qs，tg，T的關系方程組，即公交站點停靠線路發車頻率與上游交叉口信控參數的協調關系方程組.通常情況下，交通口的信號周期可通過相關交叉口交通量及區域控制策略分析計算得出，T可看成已知量.

公交站點停靠線路發車頻率與上游交叉口信控參數的協調關系可體現在以下2個方面：（1）下游公交站點發車頻率已定，如何確定上游交叉口信控參數；（2）上游交叉口信控參數已定，如何調整下游公交站點停靠線路的發車頻率.從關系方程組可以看到，已知信號周期T和λs，解方程組得上游交叉口的直行綠燈時間；已知信控參數T，tg，可解得下游公交站點停靠線路的發車頻率λs.因此該關系方程組從理論上確定了公交站點停靠線路發車頻率與上游交叉口信控參數的協調關系.

3 實例分析

選取南京市北京東路－丹鳳街交叉口及北極會堂公交停靠站作為實例分析對象，調查、整理得如下基本數據：上游路口信號控制周期為150s，東西直行綠燈時間65s，東西左轉綠燈時間19s，東西紅燈時間60s；交叉口進口兩直行車道車輛到達率為1 025pcu／h.北極會堂公交停靠站距離下游交叉口25m，受下游交叉口信號燈影響、站臺停靠13條線路、下游交叉口g／c＝80／154＝0.519，td＝32s，站臺車位數為4，站點公交車輛的到達率為138bus／h.

采用式（4～5）可計算得站點物理設施的通過能力為 B＝222bus／h，μ1＝76bus／h，μ2＝135 bus／h，μ3＝183bus／h.取α＝0.3根據調查得T＝150s，λs＝138bus／h，可由關系方程組解得與下游站點停靠線路發車頻率相協調的直行車流綠燈時間t′g＝53＜65s；同理，由tg＝65s，解得在間斷流條件下，滿足站點通行能力的停靠線路發車頻率的值λ′s＝107bus／h＜138bus／h.該站點高峰時段，公交車輛排隊進站車輛較多，與計算結果相吻合.可通過縮短上游交叉口東西向的直行綠燈時間和減少停靠站點線路的方法來改善當前站點車輛排隊進站較多的情況，也進一步驗證了論文推倒關系方程的正確性.

4 結束語

影響公交線路運行效率的關鍵位置之一是公交停靠站，因此合理有效的解決公交車在公交站點的效率問題將能很大程度提高公交運行的效率，提高公交出行方式的優勢.論文本著公交優先的理念，研究站點通行能力約束下，上游交叉口信控參數與下游公交站點的協調關系.對站點規劃和交叉口信控參數的設定有參考作用，同時也是公交優先理念在微觀技術上體現.

［1］HAMDOUCH Y，LAWPHONGPANICH S.Schedule－based transit assignment model with travel strategies and capacity constraints［J］.Transportation Research Part B：Methodological，2008，42（7／8）：663－684.

［2］ZHAO Xiaomei，GAO Ziyou，LI Keping.The capacity of two neighbour intersections considering the influence of the bus stop［J］.Physica A：Statistical Mechanics and its Applications，2008，387（18）：4649－4656.

［3］戴 帥，朱 晨，陳艷艷.城市公交系統的時間可靠度研究［J］.武漢理工大學學報：交通科學與工程版，2008，32（5）：869－871.

［4］Federal Transit Administration.Transit capacity and quality service manual 2nd edition［R］.Washington D C：Transit Cooperative Research Program （TCRP）Report 100，2003.

［5］柏海艦，李文權.常規公交站臺容納線路能力計算模型［J］.東南大學學報：自然科學版，2007，37（6）：1077－1080.

［6］柏海艦，李文權，孫 山.基于車流特性的路內公交站點通行能力［J］.系統工程理論與實踐，2009，29（10）：174－179.

［7］美國交通工程師協會.道路通行能力手冊（HCM）［M］.任福田，譯.北京：建筑工業出版社，1991.

［8］姚祖康.道路與交通工程系統分析［M］.北京：人民交通出版社，1996.

［9］朱全新，舒小保.兩類生滅過程的特征數及其概率意義［J］.高校應用數學學報：A 輯，2006，21（3）：311－320.

［10］王 煒，過秀成.交通工程學［M］.南京：東南大學出版社，2000.

［11］吳永欣.受公交停靠站影響的道路通行能力分析［J］.交通與運輸，2010（S2）：55－58.

［12］李秀文，榮 建.快速路分、合流影響區交通特性及通行能力研究［J］.公路交通科技，2006（1）：44－48.

［13］周 偉，王秉綱.路段通行能力理論探討［J］.交通運輸工程學報，2001（2）：50－53.