雙譜切片的分形特性在減壓閥故障診斷中的應用*
吳文兵 黃宜堅
(①福州外語外貿學院計算機系,福建福州 350018;②廈門大學信息科技學院,福建廈門 361000;③華僑大學機電工程學院,福建泉州 362021)
液壓系統中的減壓閥是液壓系統中比較容易發生故障的一種元件,如何對這種發生故障的元件進行診斷,對液壓系統的維護有著重要意義。本文在獲取減壓閥正常信號與故障信號的基礎上,通過建立AR模型,獲取正常狀態和故障狀態下信號的AR雙譜切片,再根據其自相似性,采用分別計算其容量維數的方法來進行故障診斷。
1 雙譜切片
設平穩隨機過程的 k 階累積 ckx(τ1,τ2,…,τk-1),定義為隨機變量{x(n),x(n+ τ1),…,x(n+ τk-1)}的k階聯合累積量:
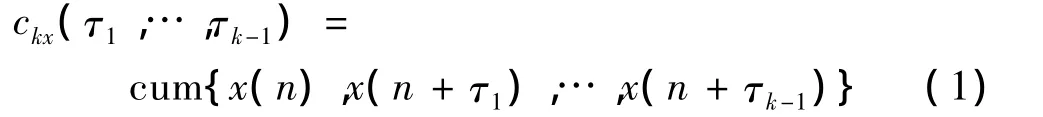
其中,cum(·)代表聯合累積量。
k階累積量譜定義為k階累積量的k-1維Fourier變換,即
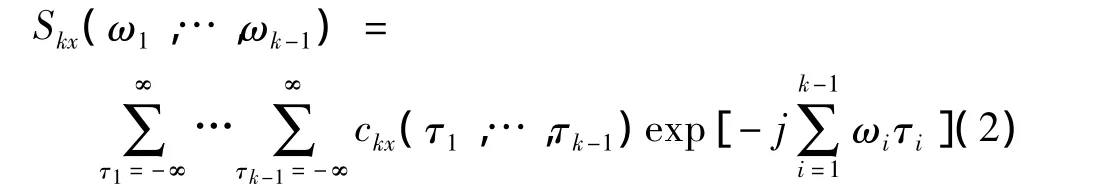
建立AR模型后,根據式(3)可以得到AR雙譜表達式為
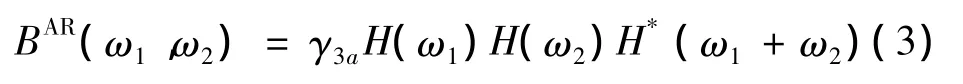
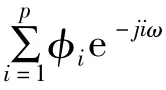
在式(4)中,設ω1=ω2時,即得到AR雙譜的1.5維(對角)切片表達式為
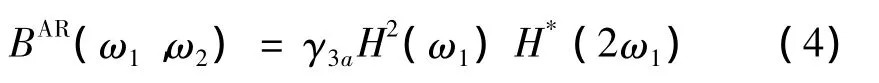
雙譜對角切片保留了雙譜的相關信息。本文選用對角切片與AR功率譜進行故障診斷的對比分析。
2 容量維
具有某種自相似性的圖形或集合稱為分形。大自然中存在的不規則的物體,可能存在不同尺度上的相似性,稱為自相似性。自相似性就是局部與整體相似,局部中又有相似的局部,每一小局部中包含的細節并不比整體所包含的少,不斷重復的無窮嵌套,它不但包括嚴格的幾何相似性,而且包括通過大量的統計而呈現出的自相似性。為了解決這類物體的維數計算,發展了計算容量相似維數方法。常用的容量維數分析方法有變方法、結構函數法、自仿射法以及盒子覆蓋算法。其中盒子覆蓋算法簡單、快速、精確。本文采用盒子覆蓋算法來計算功率譜的容量維數。計算相似比時,采用圓片(或方塊)去填充(或覆蓋)被測對象,統計覆蓋所需的方塊數來計算其維數。如此方法計算的維數稱為容量維數。如果用長度為r的尺子去測長度為L的線段,L與r之比為N。N值的大小與r長短有關,r越小,N越大。對于Dc維物體:
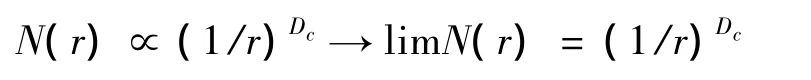
取對數得容量相似維數:
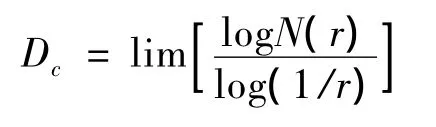
3 數據采集
當減壓閥進出油口有異物,壓力偏高或偏低都會影響到減壓閥的正常運行。為了獲取減壓閥在故障狀態下的運行信號,本文進行的實驗特設置故障如下:人為在減壓閥進油口加φ3 mm的鐵芯,通過實驗可以近似模擬減壓閥工作故障狀況。
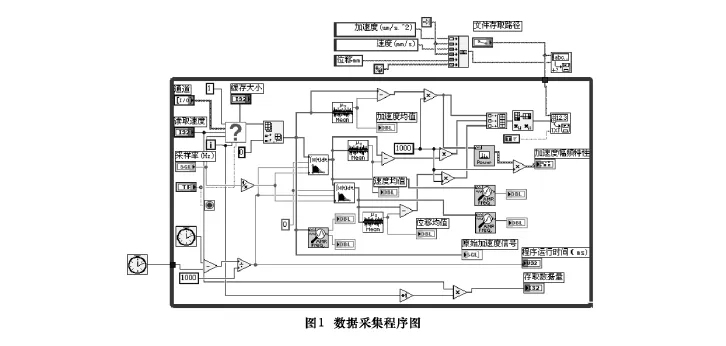
本文振動信號的采集和處理使用的軟件是Lab-VIEW。利用LabVIEW及PCI-6014的數據采集卡和1個加速度傳感器,依次采集減壓閥在正常和故障狀態下的振動信號。實驗數據采集程序如圖1所示。在每種測量中,將油路壓力從1~5 MPa分6個壓力等級。采樣頻率250 Hz,讀取頻率125 Hz,采樣過程時間約2 min。本文實驗使用的數據個數為2 000個。
測控系統的硬件有計算機、PS-3030D直流電源(固緯電子有限公司)、ST-1-03型非接觸式電渦流位移傳感器(北京昆侖海岸公司)、數據采集卡PCI-6014以及接線端子8LP(NI公司)。由于測試過程中系統外部和內部各種因素的影響必然在輸出過程中夾雜著不需要的成分,本文采用中值法對采集的振動信號進行預處理剔除混雜在信號中的干擾噪聲。
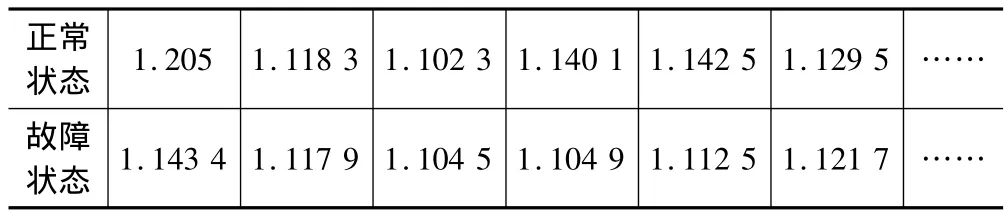
表1 雙譜切片容量維數值表
4 雙譜切片
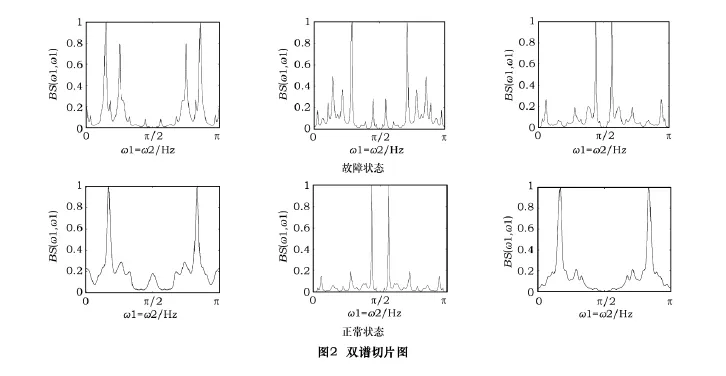
本實驗首先分正常和故障狀態分別各獲得13組數據,之后又分別得出這26組數據的雙譜對角切片,本文分別選取油壓為1 MPa、3 MPa、5 MPa時測得的兩種振動狀態下的各3組數據,將其雙譜切片示于圖2。圖中橫軸表示圓頻率,縱軸表示歸一化后的幅值大小,無量綱。由圖2可以看出,故障狀態的雙譜切片相對于正常狀態來說,底部更窄,波峰顯得更細更尖銳,也更復雜一些,這種特性使得兩種狀態的雙譜切片有可能呈現出不同的自相似性,本文就利用了這種特性進行故障診斷。
5 實驗結果分析
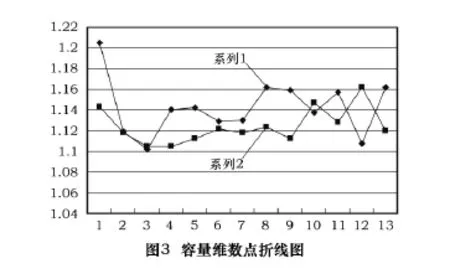
本次實驗一共獲取了26組數據,正常狀態和故障狀態各13組。為了對所獲得的信號進行定量分析以便進行故障判別,首先計算出每組數據的AR功率譜。本文為了有效判別故障,利用容量維作為工具,分別計算正常狀態和故障狀態的容量維數,其結果見表1。為了對結果進行有效觀察,特繪制了表1的點折線圖,見圖3。其中系列1代表正常狀態數據,系列2代表故障狀態數據。從圖中可以看出,正常狀態下信號的容量維數在整體上明顯大于故障狀態下的容量維數,如果設定一個閾值1.128 1,以是否大于這一閾值作為有無故障的判別依據,則在正常狀態,大于這個閾值的有10組數據,在故障狀態下小于這個閾值的也是10組,則本實驗得出的總體正確識別率接近80%,說明本文提出的方法是可行的。
6 結語
本文通過建立AR模型,獲取了減壓閥在正常信號和故障信號時的AR雙譜切片,根據雙譜切片所體現出來的自相似性,通過計算容量維數,提出了一種根據AR雙譜切片的容量維數進行故障診斷的方法。實驗結果證明本文的方法是可行的。由于AR雙譜能有效去除高斯噪聲,并能保留信號間的相位耦合信息,本文提出的方法相對于其他方法進行的故障診斷具有一定優勢。
[1]張賢達.時間序列分析—高階統計量方法[M].北京:清華大學出版社,1996:21-122.
[2]COLLIS W B,WHITE P R,HAMMOND J K.Higher-order spectra:the bispectrum and trispectrum[J].Mechanical Systems and Signals Processing,1998,12(3):375 -394.
[3]張嚴,王樹勛.非線性相位耦合的切片譜分析方法[J].電子學報,1998,26(10):104 -109.
[4]孫暉,趙菁,朱善安.基于切片雙譜分析的滾動軸承故障識別研究[J].浙江工業大學學報,2005,39(6).
[5]彭志君,黃宜堅.基于AR雙譜的溢流閥故障診斷[J].機械科學與技術,2007,26(7):908 -912.
[6]張仁鐸.空間變異理論及應用[M].北京:科學出版社,2005.
[7]趙旭.關于分形統計學研究的若干問題[J].統計與決策,2006(4):19-20.

