基于改進自適應遺傳算法求解機床制造企業立體倉庫堆垛機路徑優化問題

周耿烈 馮無恙 胡赤兵②

(①蘭州理工大學機電工程學院，甘肅蘭州 730050;②蘭州理工大學數字制造技術與應用省部共建教育部重點實驗室，甘肅蘭州 730050)

成本、質量、生產率和產量、交貨期是衡量機床制造企業生產能力和巿場競爭能力的4個要素［1］。機床零部件加工后要經過嚴格的檢驗進入全自動化立體倉庫存放，再由立體倉庫送至裝配作業線進行部件裝配，裝配完成的部件經過嚴格的部裝檢驗后進入立體倉庫。立體倉庫根據生產需要將零部件送到裝配作業線進行總裝。如何在保證機床質量的前提下降低生產成本包括物流成本，同時提高機床的生產率和產量，并依據客戶要求按時交貨是機床制造企業關注的重點。

立體倉庫是現代物流系統中迅速發展的一個重要組成部分，在制造自動化中也占有非常重要的地位。在機床制造企業建立立體倉庫及其信息管理系統其目的不僅是為了進行毛坯、半成品、成品、工裝夾具等的自動存儲和自動檢索，更是密切配合企業的產銷計劃與物料需求計劃。由于機床不同零部件的制造周期不一樣，為保證產品成套既要按期交貨，又要盡可能減少由于產品積壓所導致的生產管理混亂現象，立體倉庫管理系統是現代化立體倉庫不可或缺的一部分。

隨著自動化立體倉庫在生產線當中的應用，形成了以自動化立體倉庫為核心的物流配送系統，從采購、外協到貨、檢驗入庫、毛坯出庫、加工、零件入庫、裝配及產品生成，都要與自動化立體倉庫協調。

自動化立體倉庫要求作業迅速、準確、穩定等特點。其作業周期由出入庫臺的時間、貨物登記時間和堆垛機在倉庫存取貨物時間等組成。由于現代化立體倉庫規模越來越大，其高度達50多m，長度也達150 m，所以在整個物流周期中堆垛機的行駛時間占到整個倉庫作業周期的50%。如果堆垛機調度不當或選用效率較低的調度模式，會嚴重影響堆垛機的工作效率，進而影響整個倉庫的作業效率。所以選擇一種較為合理的揀選路徑是提高堆垛機作業效率的方法。

在對堆垛機的路徑進行分析時，國內外學者已對倉庫中的貨位存取優化，單復合作業的優化、堆垛機揀選作業的優化及輸送系統的調度優化進行了廣泛的研究。自動化立體倉庫堆垛機路徑優化的算法研究，包括蟻群算法、模擬退火算法、啟發式算法、禁忌搜索算法［2－5］及遺傳算法等。其中遺傳算法能夠得出較好的全局最優解，具有搜索速度快、精度高等優點。

1 自動化立體倉庫模型的建立

假設堆垛機的工作空間(立體倉庫)用二維平面圖形來表示。堆垛機執行一次任務時所不能通過的貨格的位置已知。用尺寸相同的柵格對立體倉庫進行劃分。若某一柵格內不含任何障礙物，則稱此柵格為自由柵格;反之，稱之為障礙柵格［6］。如圖1所示。

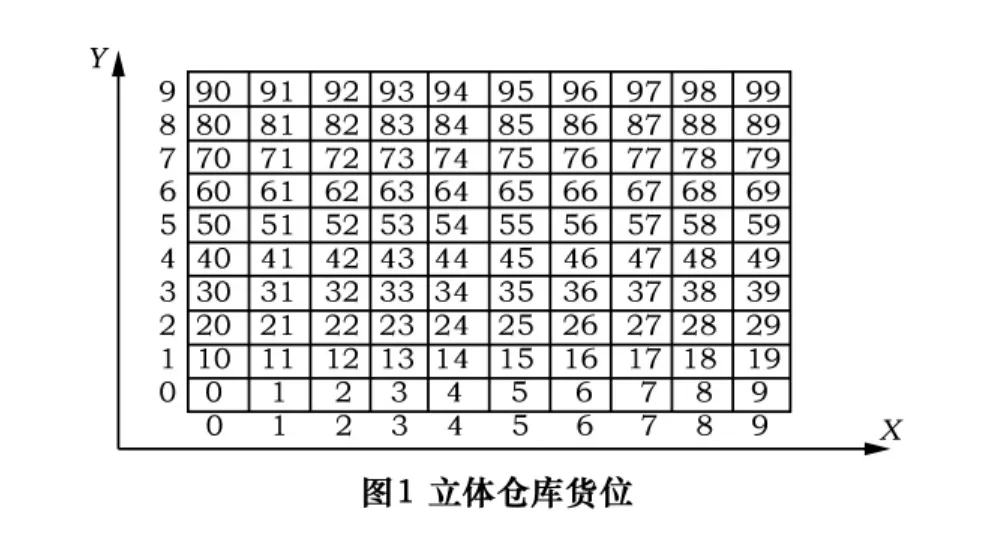
2 改進的自適應遺傳算法

遺傳算法是一種借鑒生物界自然選擇和自然選擇機制的隨機化搜索算法，對于用傳統搜索方法難以解決的復雜和非線性問題具有良好的適應性。但還有很多不足，如早熟收斂、易陷入局部最優和收斂速度慢等。本文采用改進的自適應遺傳算法對堆垛機的工作環境進行建模，找到堆垛機路徑優化的最佳路徑。

當今改進遺傳算法的措施主要集中于對交叉概率和遺傳概率的選擇與確定上，因為它們會影響遺傳算法的收斂性和搜索速度。針對不同的優化目標需要反復試驗來確定交叉概率和遺傳概率，而傳統的遺傳算法采用的是固定數值來代替交叉概率和遺傳概率，這樣很難找到最佳優化目標。

自適應遺傳算法(AGA)［7］是由 Srinivas提出來的，它的基本思想是交叉概率和變異概率能夠隨著適應度的變化而變化。當種群各個體適應度處于趨于一致或者局部最優時，使交叉概率和變異概率增加，從而避免陷入局部最優，繼而引發早熟現象;當群體各個體適應度比較分散時，使交叉概率和變異概率減少，從而不易破壞優良個體，以利于優良個體保存下來。同時，對適應度高于群體平均適應度的個體選擇較小的交叉概率和變異概率，使得個體保存下來;那些低于群體平均適應度的個體，選擇較大的交叉概率和變異概率，一方面將一部分差的個體淘汰，另一方面增加新個體［8］。在自適應遺傳算法中，交叉概率pc和變異概率pm按如下公式進行調整:

式中:fmax為種群的最大適應度;favg為種群的平均適應度;f′為參與交叉的2個個體中較大的個體的適應度;f為變異個體的適應度。

AGA算法是有缺陷的。從公式中可以看出，當個體適應度越接近于最大適應度(fmax－f′≈0)時，交叉概率和變異概率越小，到接近為零，這種調整方法在群體優化后期較為合適，因為在后期，要將優良個體保存下來，即為全局最優解。但是在進化初期不利，因為在進化初期群體中的較優個體幾乎處于一種不發生變化的狀態，而此時的優良個體不一定是全局最優解，增加了進化走向局部最優解的可能性，就是所謂的早熟現象。

任子武等人在AGA的基礎上，提出了一種改進的自適應遺傳算法(IAGA)。它除了有AGA的一系列優點之外，還彌補了AGA的缺陷。為了保證每一代的優良個體不被破壞，采取了精英保留策略:如果下一代的最佳個體適應度小于當前種群的最佳個體適應度，那么將當前種群的最佳個體或者多個個體直接復制到下一代，從而不會被當代種群的交叉和變異等遺傳操作破壞［8］。IAGA 公式如下:

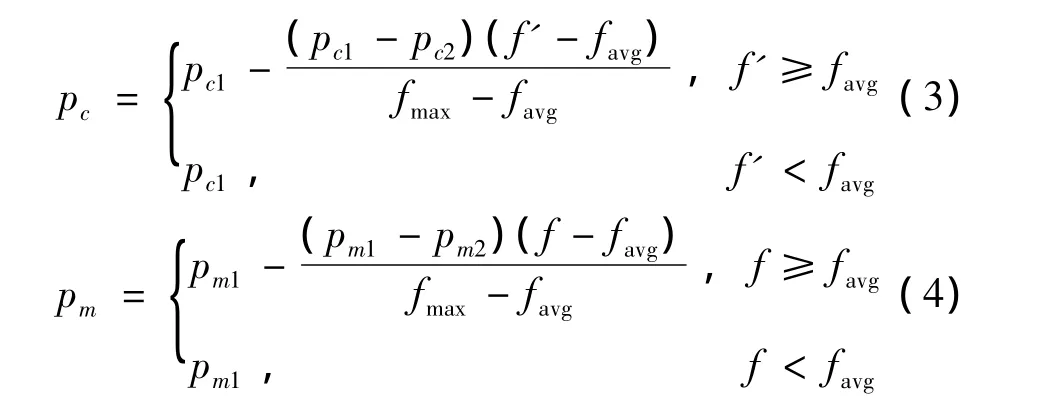
式中:pc1、pc2分別為交叉概率的最大值和最小值;pm1、pm2分別為變異概率的最大值和最小值。

在IAGA算法中，根據公式，個體的交叉概率和變異概率應根據個體的適應度在平均適應度和最大適應度之間進行線性變換。如果種群中存在較大規模的適應度接近平均適應度的個體，它的交叉概率最大，幾乎為pc1和pm1，若個體適應度接近于最大適應度，那么它的交叉概率和變異概率很小，為pc2和pm2，即IAGA的自適應交叉概率和變異概率曲線非常陡峭，導致一部分個體只能擁有較低的交叉概率和變異概率，使進化停滯不前，造成局部收斂［9］。

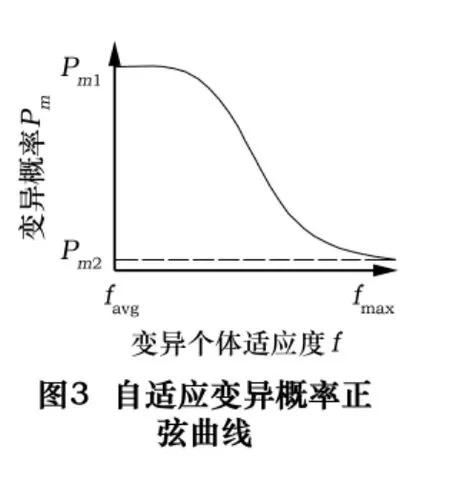
本文所要提出的新的改進自適應遺傳算法是根據種群的大小、適應值的分布情況、自適應變化整個種群的交叉概率和變異概率，使它們的變化曲線為一個從振蕩而逐漸穩定的形勢。設計進化前期具有較大的交叉概率和變異概率，以增強搜索能力，在進化后期采取相對較低的交叉概率和變異概率，以確定最佳個體。本文將采用正弦形式的自適應遺傳算法(SAGA)，其公式如下:

圖2和圖3為兩個公式所表示的圖像，均為正弦式圖像，從而保證了交叉概率和變異概率呈一種穩定式變化，而不會出現過度陡峭曲線，因為－1＜sina＜1，它可以弱化由于適應度接近平均適應度或者接近最大適應度而造成的交叉概率和變異概率的過大或者過小，也克服了由于種群停滯不前而陷入局部最優的現象。

3 路徑規劃方法

3.1 編碼

采用序號法。基本順序是從左到右，從下到上。將立體倉庫分為若干個空格，從立體倉庫的左下角的第一個格開始，給每一個空格一個序號N，依次延續，這樣序號N與立體倉庫的每一個空格一一對應。

我們將堆垛機在立體倉庫的一條運動路徑稱之為一個個體，在這里假設堆垛機由起始位置A經過這一條路徑最終到達終點位置B，那么這條路徑可以表示為一個個體。采用序號法，則表示為以下所示:(0，1，11，13，22，32，34，45，56，66，77，87，88，99)，我們從中可以看出，每條路徑采用序號法具有編碼長度短、簡明、直觀的優點。

3.2 初始種群

在選取初始種群時，為了使堆垛機行駛的路徑最短，在起始點與終點連線的兩側分布初始點，把這些點稱之為過渡點。把上一點與下一點的選取作為一個周期，每個周期選擇與當前堆垛機的位置距離最小的點作為當前時刻的規劃子目標點。如果子目標點不是障礙物，則此點為最佳點;若是障礙物，則選取此點周圍的過渡點為候選點。這樣規劃出的路徑都是圍繞起點和終點連線的，確保點的分布不會太分散，這樣可以規劃出最短路徑。

3.3 個體適應度函數

在這里選取如下所示的個體適應度函數:

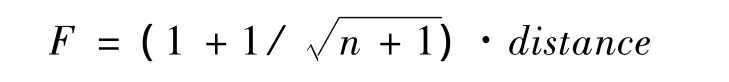
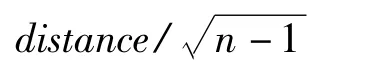
3.4 遺傳算子設計

3.4.1 選擇算子

采用輪盤賭選擇和精英保留相結合的方法，是個體按照與適應度成正比例的概率向下一代群體繁殖。

3.4.2 交叉算子

采用部分匹配交叉法:先隨機產生兩個 ，定義這兩點間的區域為匹配區域，并用位置操作交換兩個父代的匹配區域。如:交叉點為3、6父代A872 130 9546父代B983 567 1420，先交換130與567，得出來的兩個過渡代為A′872 567 9546父代B′983 130 1420，對于A′、B′中的匹配區域以外出現的數碼重復，要依據匹配區域內的位置逐一進行交換。即5和1進行交換，6和3進行交換，7和0進行交換。這樣經過交叉之后，子代A為 8025679143，同理，子代B為9861305427。

3.4.3 變異算子

其變異算子采用逆轉變異算子，方法如下:在個體中隨機挑選兩個逆轉點，再將兩個逆轉點間的基因反序插入原位置。如個體A:987654321，在第4號位與第6號位采用逆轉變異算子。新生成的個體為987456321。

3.4.4 平滑算子

堆垛機采用導軌式行走裝置，所以在行駛到轉彎路徑時要求拐彎處角度大，從而引出路徑平滑度問題。平滑度是指路徑段之間偏轉角度的大小。如果轉角過小，則會增加堆垛機行走過程的復雜性，其消耗時間過長，甚至會導致堆垛機因轉角過小而無法通過。

平滑算子是在路徑段之間的轉角處兩端添加兩個或多個節點，替代原有的節點，使得路徑轉角處更加平滑，使堆垛機順利通過此處。

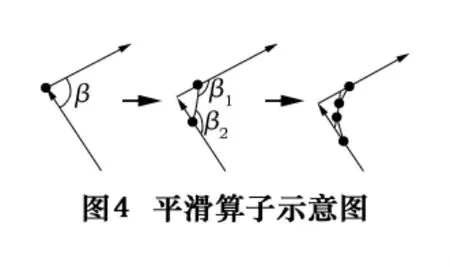
設堆垛機的轉彎最小角度為α，如圖4所示.當判斷出兩個相連路徑的拐角偏轉角度β＜α時，則分別在拐角附近的兩端可行域附近隨機選取兩個新節點，這樣就形成了兩個拐角處，這時分別判斷兩個拐角處的偏轉角度是否大于α，若大于則替代原節點，否則在兩節點處的兩端可行域再選擇兩個新節點，直至符合要求。

4 仿真分析

采用Matlab遺傳算法工具箱對此進行仿真測試。設種群規模為40，每個種群的長度為20，交叉概率pc=0.9，變異概率為pm=0.01，然后利用SAGA對每一代的交叉概率和變異概率進行計算。在Matlab窗口中輸入Gatool，打開、進入遺傳算法工具箱。之前必須將適應度函數寫成M文件。

決定遺傳算法的一個重要性能是種群的多樣性。個體間的距離越大，則多樣性越高;反之，個體間的距離越小，則多樣性越小。

設置“initial range”為［0;1］，其顯示圖形如圖 5所示。

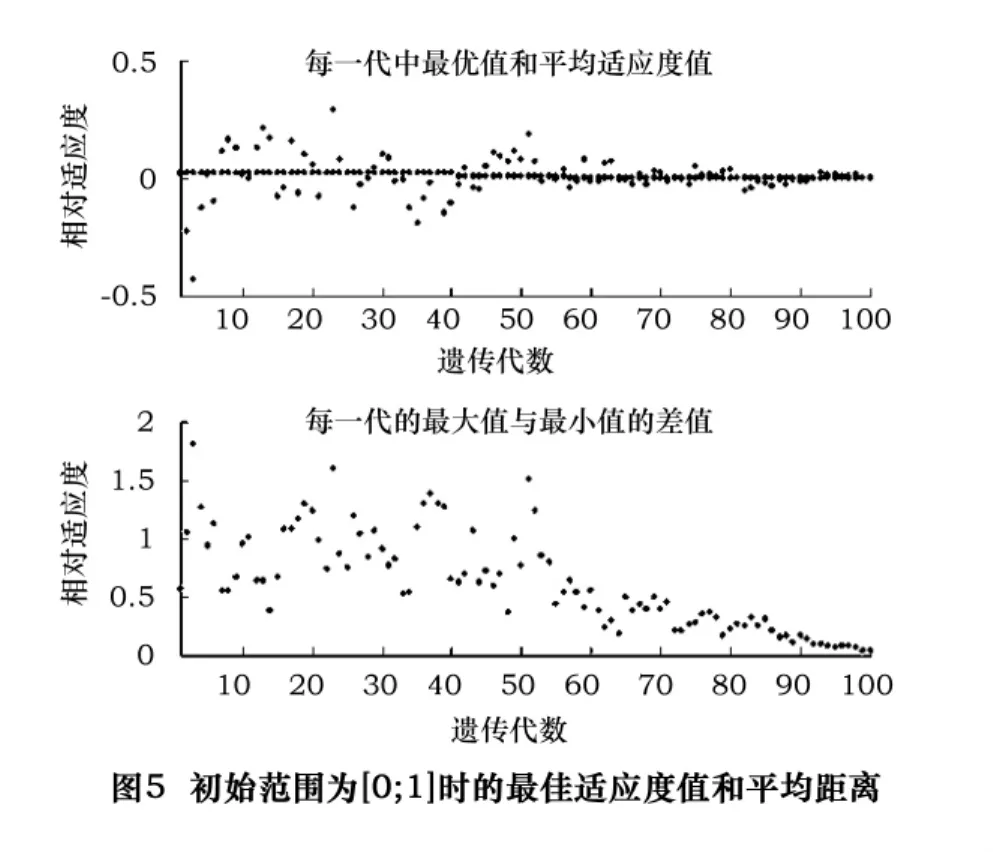
圖5的上圖中較為密集的點為每一代的最佳適應度值(Fitness value)，而在密集點周圍的較為分散的點為每一代的平均適應度值，它可以很好地用來衡量種群的多樣性。對于初始范圍的設置，由于多樣性太小，算法進展很小。設置“initial range”為［0;100］，運行算法，如圖6所示。

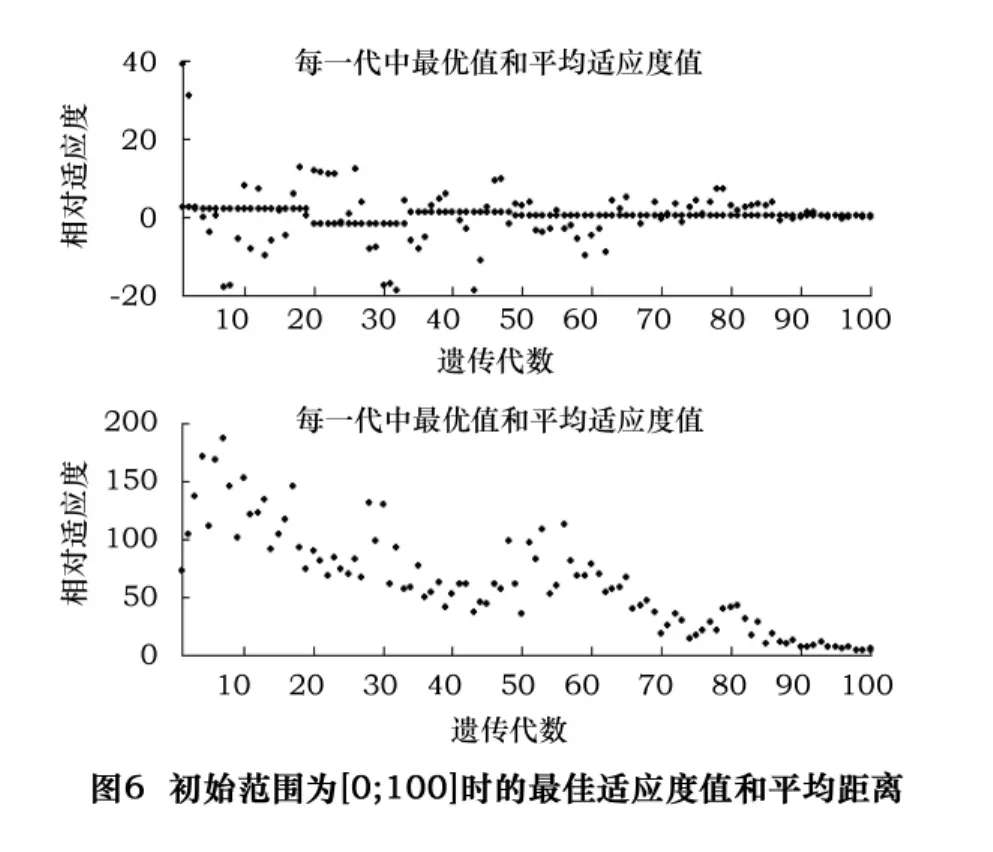
這次算法進展較快。但是，由于個體之間的平均距離較大，最佳個體原理最優解。

設置“initial range”為［0;20］，運行算法，如圖7所示。

這次由于多樣性比較適合，所以算法得到的結果比前兩次都好。

圖7上圖為遺傳算法過程中群體中每一代個體最佳適應度隨進化代數(Generation)的變化情況。可以看出，改進后的遺傳算法收斂較快，進化到約34代就已經接近搜索到了全局最優解。在早期各代中，當個體離理想值較遠時，最佳值會迅速得到改進;在后來各代中，種群越接近最佳點，最佳值改進的越慢，正好順應了SAGA的要求，圖7的下圖很好地解釋了這些情況。它為每一代中(每一代中會產生一定數量的點，各點所對應的適應度值不一樣)各點之間的平均距離。當變異數減小時，個體之間的平均距離也減小，逐漸向零靠近。可以看出，當進化代數在40代之前，個體之間的平均距離較大，這符合了SAGA的要求，即在進化前期，不要一味地將適應度值差的個體淘汰掉，而是要通過交叉和變異將個體改良，這樣既增加了種群的多樣性，又不至于產生局部最優化，導致引起的早期收斂現象。而從第40代往后，個體之間的平均距離減小，這意味著代與代之間的差異性較小，全局最優解基本產生了。

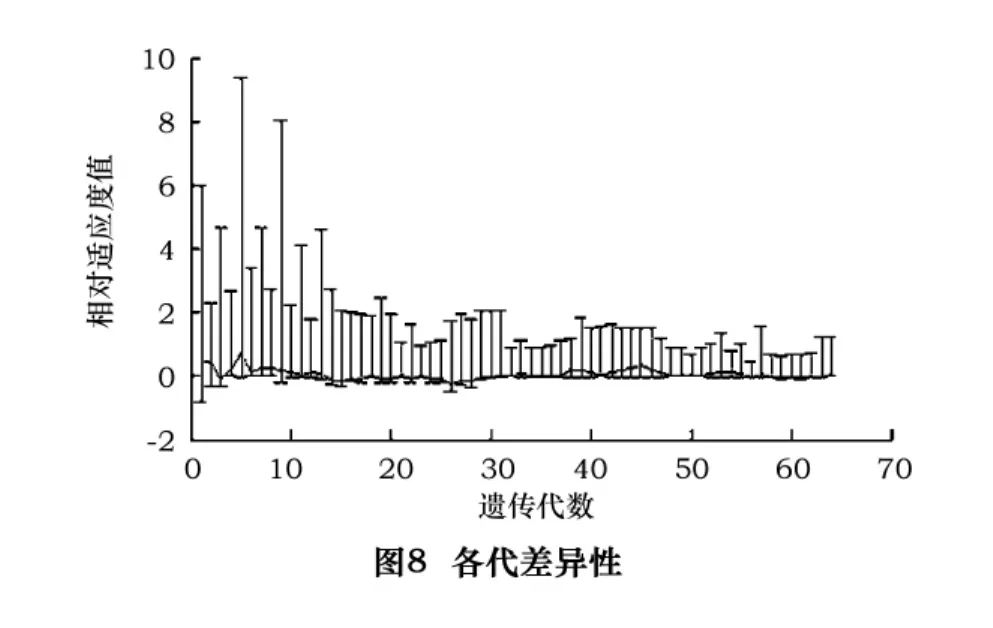
通過圖8所示可以清晰地看到自適應算法在算完100代之后，這其中的每一代的具體情況，圖8中每一條的垂直線表示每一代中各點適應度值由最小到最大的范圍，在圖形的下方所看到的一條曲折的線是遺傳算法在完成進化100代之后平均適應度值演化趨勢。40代之前，每一代的種群之間適應度差異較大，所以線條長度較長;而40代之后，差異性迅速縮小并趨于穩定化，所以線條長度較短。與此相對應的是平均適應度也由較大范圍的變化逐漸縮小并最終趨于穩定。這說明當變異數減小時，適應度值的范圍也減小，這些圖形顯示減小變異數，也就減小了子輩的多樣性，加快了收斂速度，這說明全局最優解接近產生了。

5 結語

本文提出改進的自適應遺傳算法(SAGA)，不僅克服了傳統遺傳算法的早熟和收斂速度慢問題，而且大幅度提高遺傳算法的工作效率。此方法應用于堆垛機的路徑規劃，可提高堆垛機的路徑規劃質量和工作效率。通過Matlab遺傳算法工具箱的仿真，進一步驗證了此方法的有效性和可行性。通過自動化立體倉庫技術和軟件技術實現對物料的智能化管理，減少產品積壓，提高機床制造企業在激烈市場中的競爭能力。

［1］馬千里.機床制造企業立體倉庫信息管理系統研究［J］.控制管理，2008，4(3):5 －7.

［2］華紅艷，張丹.基于蟻群算法的自動化立體倉庫路徑優化［J］.計算機技術與自動化，2010，29(1):51 －54.

［3］杜宗宗，劉國棟.基于混合模擬退火算法求解TSP問題［J］.計算機工程與應用，2010，46(29):40 －42.

［4］陸文，郭延濤，李文杰.基于改進遺傳算法的車間調度問題求解［J］.現代制造工程，2010(10):35－37.

［5］王清校，郎茂祥，彭永昭，等.基于禁忌搜索算法的貨物運輸路徑和方式選擇問題研究［J］.物流技術，2010(12):96－98.

［6］孫樹棟，曲彥賓.遺傳算法在機器人路徑規劃中的應用研究［J］.西北工業大學學報，1998，16(1):79 －83.

［7］SRINVAS M，PATNAIK L M.Adaptive probabilities of crossover and mutation in genetic algorithms［J］.IEEE Trans on Systems，Man and Cybernetics，1992，24(6):656 －667.

［8］張京釗，江濤.改進的自適應遺傳算法［J］.計算機工程與應用，2010，46(11):53 －55.

［9］任子武，傘冶.自適應遺傳算法的改進及在系統辨識中應用研究［J］.系統仿真學報，2006，18(1):41 －46.

［10］張國強，彭曉明.自適應遺傳算法的改進與應用［J］.艦船電子工程，2010(1):83－84.