一類對稱函數的性質及其應用

劉清華，余 啟，張 昱

（南華大學 數理學院，湖南 衡陽 421001）

1 定 義

Schur凸函數的概念由I.Schur于1923年引入，它不僅在建立解析不等式方面發揮著極大的作用，而且在統計學，經濟學以及其它方面也有著許多重要的應用（詳見Marshall和Olkin的專著［1－2］）。下面的定義可參見文獻［2－5］。

對于向量x＝ （x1，x2，…，xn），把其分量排成遞減次序后記為：x［1］≥x［2］≥ … ≥x［n］。

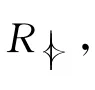
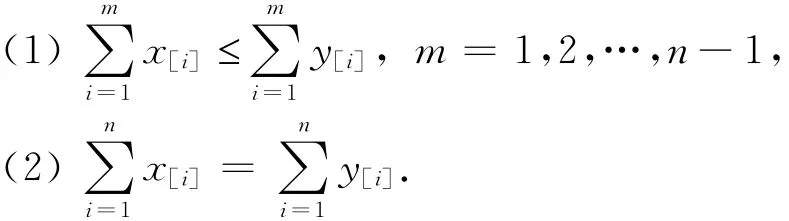
則稱x被y所控制（記為x?y）。

定義1.2 定義在集合Ω?Rn上的實函數φ稱為Ω上的Schur凸函數，如果

在Ω上x?y?φ（x）≤φ（y）。

如果對于任意的x?y且x不是y的一個重排，有φ（x）＜φ（y），則稱φ為Ω上的嚴格Schur凸函數。φ在Ω上為Schur凹（嚴格Schur凹）的，當且僅當－φ在Ω上是Schur凸（嚴格Schur凸）的。

判斷函數f（x）為Schur凸函數，有下面的Schur條件。

定理1.3 設Ω?Rn是非空的對稱凸集，函數f：Ω→R在Ω上連續且在Ω的內部Ω0可微，則f為Ω上的Schur凸函數當且僅當f為Ω上的對稱函數，且對于所有x∈Ω0，

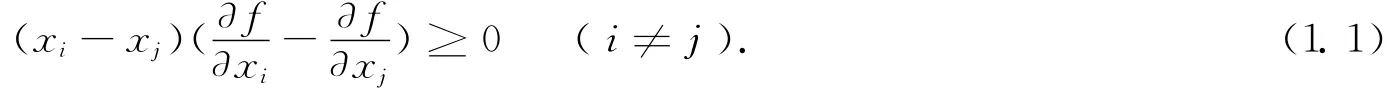
如果不等式（1.1）對于xi≠xj（1≤i，j≤n）是嚴格的，那么f為嚴格Schur凸的。

由于f（x）是對稱的，則Schur條件（1.1）可簡化為［2］

如果（1.2）對于x1≠x2是嚴格的，那么f為嚴格Schur凸的。如果不等式（1.1）或（1.2）反向，那么f為Schur凹的。

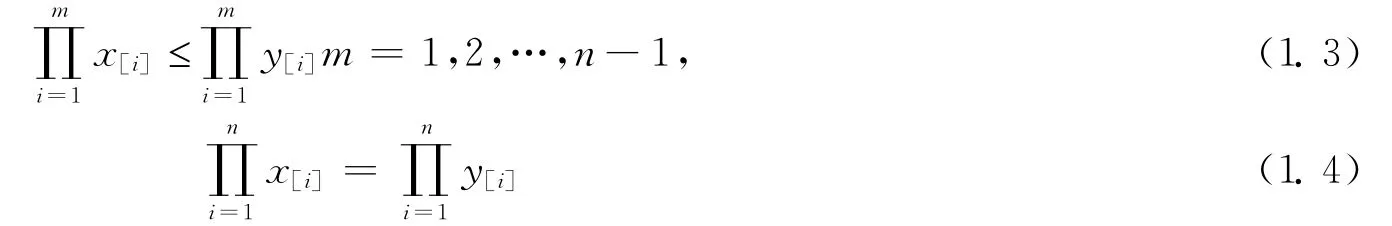
則稱x被y對數控制，記為lnx?lny.

定義1.5 設I是 （0，∞）的子區間［7］，函數f：In→ （0，∞）稱為Schur幾何凸的，如果在In上lnx?lny?f（x）≤f（y）；函數f稱為Schur幾何凹的，如果In上lnx?lny?f（x）≥f（y）.

定理1.6 設f（x）＝f（x1，x2...xn）為對稱的［7］，且在In上有連續偏導數，那么f：In→ （0，＋∞）為Schur幾何凸函數當且僅當

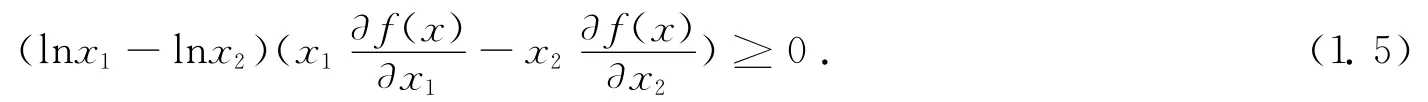
如果不等式（1.5）反號，則f為Schur幾何凹的Marshall和Olkin在文獻［2］中研究了函數

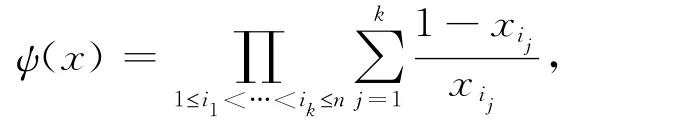
的Schur凸性問題，這里0＜x1＜1，i＝1，2，...n.

本文研究Ψ（x）的對偶形式：

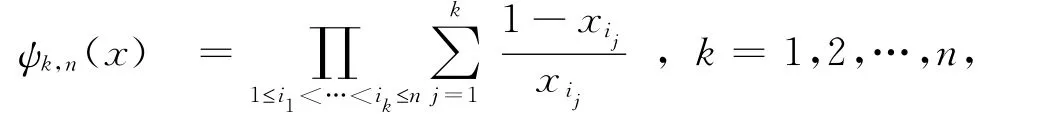
其中，0＜x1＜1，i＝1，2，...n. 我們將討論此函數的Schur凸性和Schur幾何凸性問題，并利用“優化理論”建立一些解析不等式。

2 Ψk，n（x）的 Schur凸性

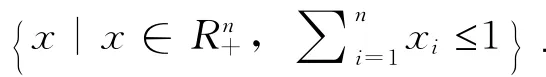
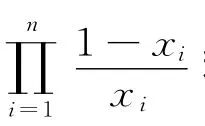
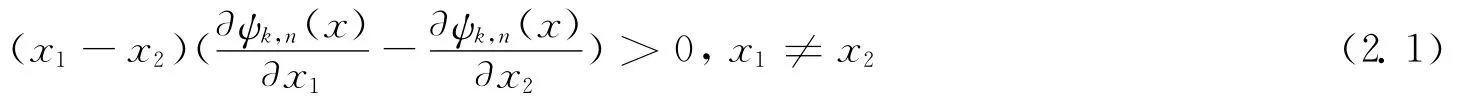
為此，我們分兩種情形進行討論。

情形1. 當k＝2時，直接計算可得

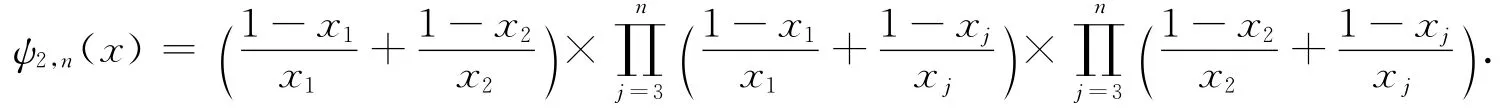
取對數并求導，可得

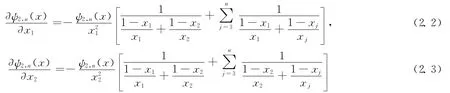
于是，當x1≠x2時，我們有

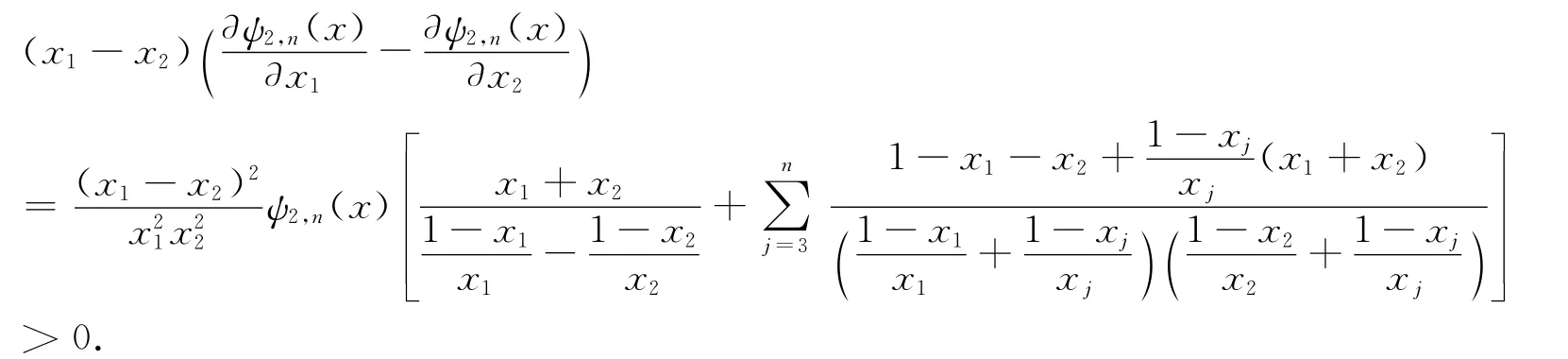
情形2. 當3≤k≤n－1時 ，我們不難得到

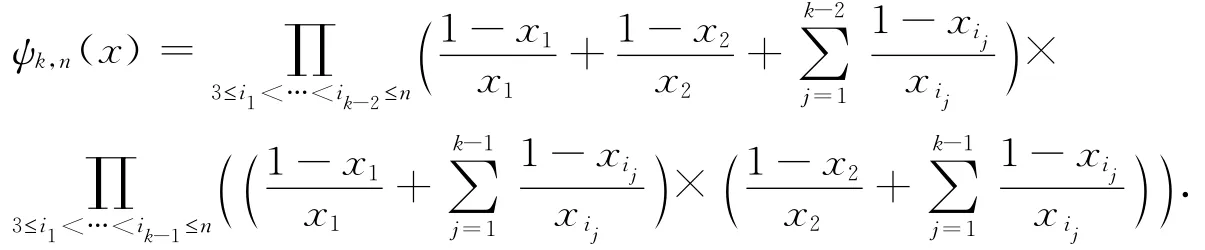
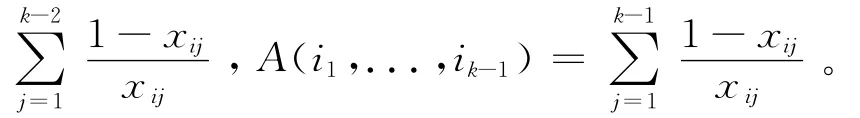
取對數并求導，得到

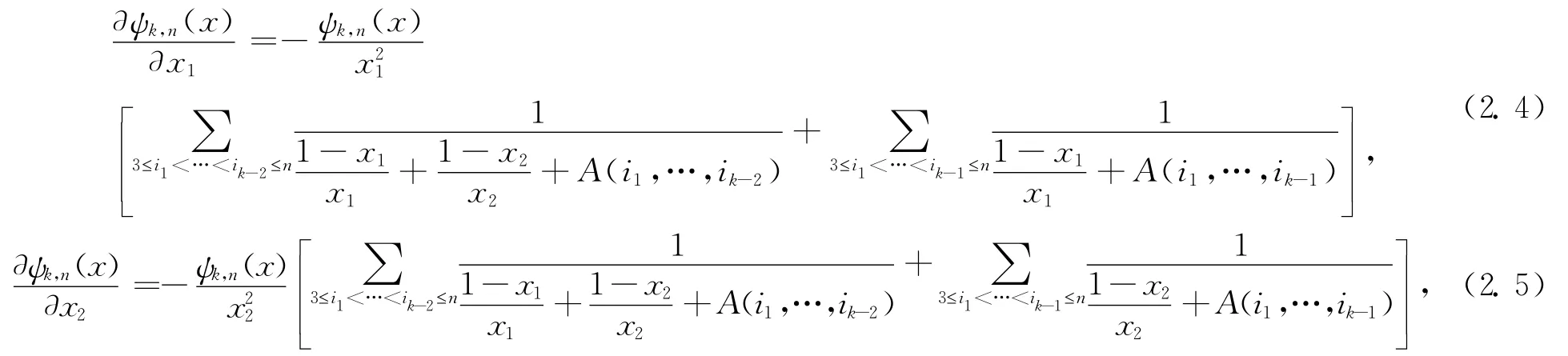
當x1≠x2時 ，由（2.4）和（2.5）可得

綜合上述，定理得證。

類似定理2.1的證明，我們還可以得到下面的

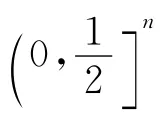
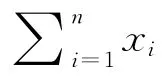
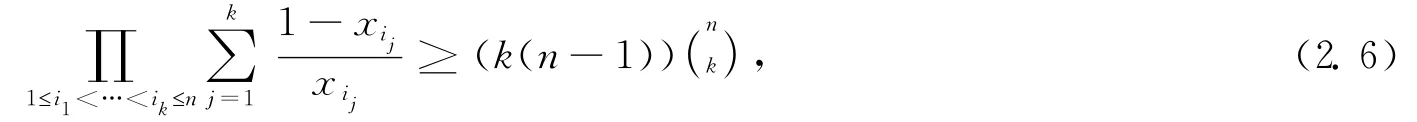
特別地

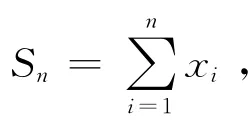
當且僅當x1＝...＝xn時等號成立。

注：（2.7）為Mewman不等式［2，（2.8）為Shapiro不等式［3。這樣，我們重新建立和推廣了這些不等式。

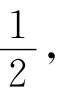
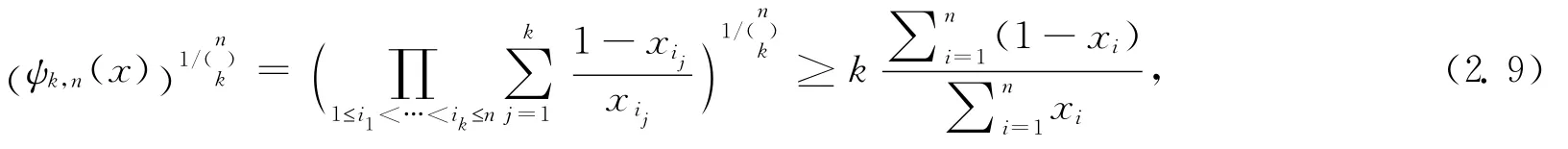
當且僅僅當x1＝...＝xn時等號成立

注：如果在 （2.9）中取k＝1，可得著名的 Ky Fan不等式［1，p.5；4，p.363］：

當且僅當x1＝...＝xn時等號成立。

3.Ψk，n（x）的Schur幾何凸性

定理3.1 設xi＞0，i＝1，2，...，n（n≥3），那么

（1）函數 Ψ1，n（x）在 0，（1）n是Schur幾何凹的；

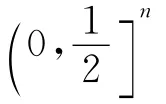
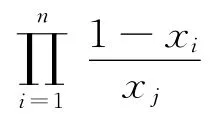
求導得

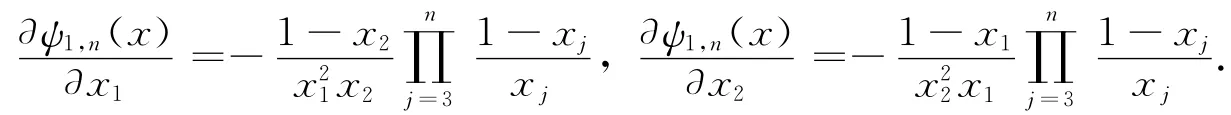
因此，當x1≠x2時，我們有

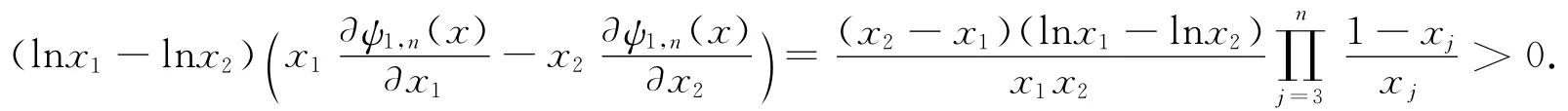
由定理1.6，Ψ1，n（x）在 （0，1 ）n上是Schur幾何凹的。

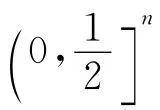
情形1. 當k＝2時，由（2.2）和（2.3）可得

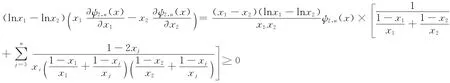
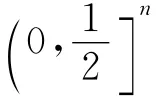
情形2. 當3≤k≤n 時，根據（2.4）和（2.5），直接計算可得

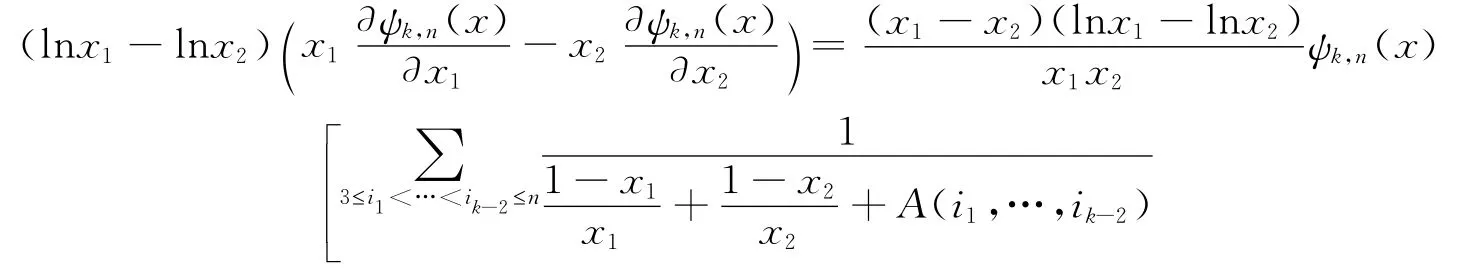
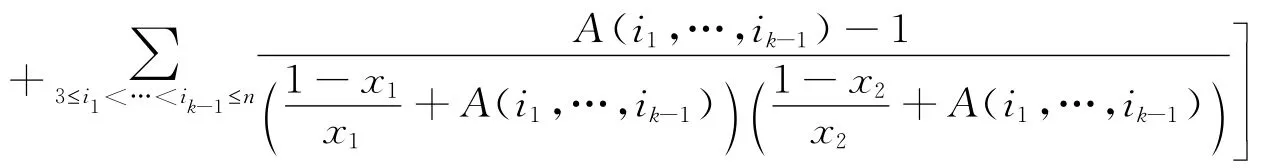
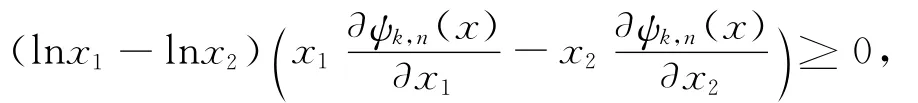
再根據定理1.6，Ψk，n（x）是Schur幾何凸的。定理證畢。

證明： 利用定理3.1并注意到ln（G（x），...，G（x））?ln（x1，....，xn），即可得到該推論。

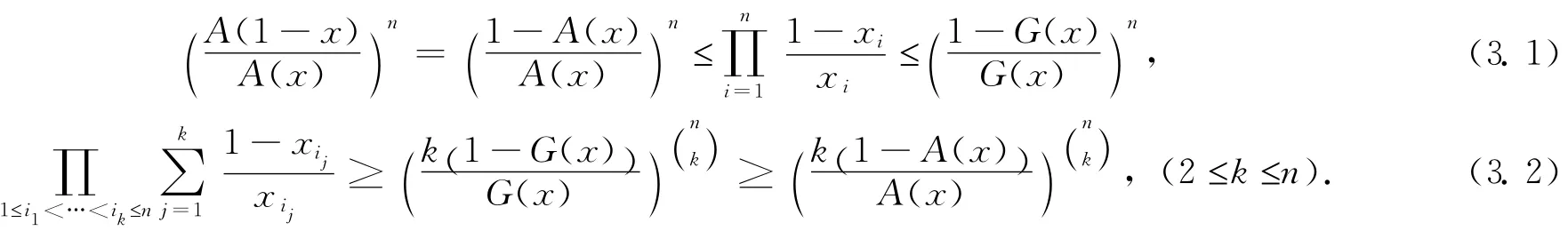
［1］E.F.Beckenbach and R.Bellman.Inequalities［M］.Berlin：Springer－Verlag，1961.

［2］A.W.Marshall and I.Olkin.Inequalities：Theory of Majorization and Its Application［M］.New York：Academic Press，1979.

［3］匡繼昌.常用不等式［M］.3版.濟南：山東科技出版社，2004.

［4］D.S.Mitrinovic.Analytic Inequalities［M］.New York：Springer－Verlag，1970.

［5］J.Pecaric，F.Proschan，and Y.L.Tong.Convex Functions，Partial Orderings，and Statistical Applications［M］.New York：Academic Press，1992.

［6］C.P.Niculescu，Convexity according to the geometric mean［J］.Math.Inequal.Appl.，2000，3（2）：155－167.

［7］張小明.幾何凸函數［M］.合肥：安徽大學出版社，2004.

［8］F.Z.Zhang，Matrix inequalities by means of block matrices［J］.Math.Inequal.Appl.，2001，4（4）：481－490.