基于未確知測度的人才綜合測評模型

薛俊鋒，李 莉，趙子月，夏自強

(1.邯鄲市邯三建筑工程有限公司，河北邯鄲056001;2.河北工程大學土木工程學院，河北邯鄲056038;3.新興鑄管股份有限公司，河北邯鄲056300)

傳統的人才測評技術大都是定性分析［1]，其專家系統實際上是一個二值結構的邏輯系統［2]，只在“是”與“非”之間取值，定量化研究比較少。在實際的人才測評中，經常遇到模糊或不確定的語意，無法僅僅采用“是”與“非”進行定量描述，而模糊綜合評判［3－7]適用于這種情況下的人才測評。但是，在模糊綜合評判中，作為隸屬度的可信度并沒有把測量準則作為必要的限制條件。因而，作為測量結果的隸屬度并不是測量意義上的某種測度，并且在合成可信度的推理算法上存在缺陷。

本文把定性分析與定量描述相結合，建立了基于未確知測度和指標分類權重的人才測評模型，修正了模糊綜合評判模型中的不足。在此模型中，隸屬度是嚴格測量意義上的某種可能性測度;在合成可信度的推理算法中，定義了對分類貢獻大小的指標分類權重的概念，給出了指標分類權重的計算方法，并把它用于合成可信度的計算中。

1 未確知測度模型

設x1，x2，…，xn表示 n 個待測評人員，X={x1，x2，…，xn}稱為論域;評價 xi(1≤i≤n)有 m 項指標 I1，I2，…，Im，稱 I={I1，I2，…，Im}為指標空間，測評指標可以是定量指標，更多的是定性指標;定量指標必須是可以測量的，定性指標必須定量化。用xij表示對象xi在指標Ij下的觀測值。C為評語空間 c1，c2，…，ck，是 C 的一種劃分，即)其中，ck(1≤k≤K)為第 k個評語等級［8]。

1.1 單項指標下的未確知測度

對象xi關于指標Ij的觀測值為xij，即xi處于第k(1≤k≤K)個評語等級的程度用［0，1] 上的實數具體表示，這個實數記為 μijk=μ(xij∈ck)，(1≤i≤n，1≤j≤m任意固定，k在1與K之間取值)。符號“xij∈ck”表示觀測值 xij使對象 xi處于狀態 ck，并非通常意義下元素與集合間的含義。μijk是對“程度”的測量結果，是一種可能性測度，作為一種測量結果的這種可能性測度它必須滿足通常的諸如“非負有界性、可加性、歸一性”三條測量準則［9]，即:

(1)非負有界性:0≤μ(xij∈Ak)≤1 (1≤i≤任意固定;Ak為C的任意子集)。

(2)可加性:μ(xij∈∪Ak)=

(3)歸一性:μ(xij∈C)=1。

稱滿足上述三條測量準則的μ為未確知測度，簡稱測度。μijk為對象 xi的單指標測度評價矩陣。

(i=1，2，…，n j=1，2，…，m k=1，2，…，k)

其中，μijk= μ(xij∈ck)(1≤i≤n，1≤j≤m，1≤k≤K)表示觀測值xij使xi處于ck評語等級的未確知測度。

1.2 指標分類權重

設使對象xi關于指標Ij的觀測值xij處于c1，c2…，ck各個評語等級的未確知測度向量為

ij1ij2ijkjxi處于各個評語等級的程度相同，因而無法區分出xi到底處于哪個評語等級。此時稱指標Ij對xi的分類未做出貢獻，記=0。

2)如果K個μijk中有一個μijk0=1，其余的K－1個均為0，則指標Ij使xi確定地處于評語等級，稱指標Ij對xi的分類做了最大貢獻，則這時應取到最大值。

指標Ij對xi的分類貢獻的大小可以由指標分類權重定量描述，而大小由的各個分量取值的集中與分散程度描述，而各分量取值集中與分散的程度有多種描述方法，最典型的一種是信息熵。由測度μijk所確定的信息熵［10]為

令

由信息熵的性質知:

2)當且僅當存在一個μijk0=1其余的K－1個均為0時，Vj取到最大值為1。

3)μijk取值越集中，Vj的值越近于1，反之 μijk取值越分散時，Vj的值越近于0。

令

由Vj的上述三條性質可知，由(5)式定義的wj

i正是我們感興趣的指標Ij關于xi的分類權重。

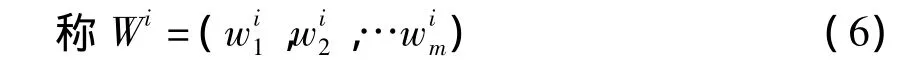
為指標I1，I2，…，Im關于xi的分類權重向量。指標Ij關于xi的分類權重是由矩陣(1)中的第 j行(μij1，μij2，…，μijk)中測度值計算得到的，或說是由Ij指標(值)提供的分類信息經計算求出來的，既然可以算出來，說明它不可能由專家主觀擬定。

1.3 綜合評價系統

若關于xi的單指標測度評價矩陣(1)已知，關于xi的各指標分類權重向量為式(6)。

令

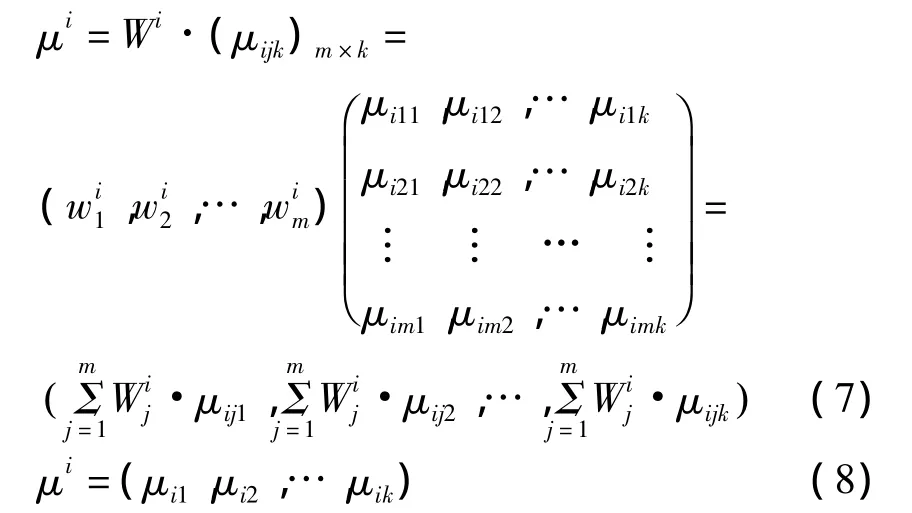
則μi為xi的評價向量。其中μijk(1≤k≤K)表示xi處于ck等級的未確知測度。式(8)具體描述了xi的不確定性分類，為了輸出確定性分類結果，需進行識別。

1.4 識別準則

因評語等級劃分是有序的，比如，第k個評語等級ck“好于”第k+1個評語等級ck+1，這種情況下最大測度識別準則不適用，改用置信度識別準則。

設置信度為 λ，(λ ＞0.5)通常取作 0.6或0.7，令

則判xi屬于第k0個評價等級ck0。真實含意是xi不低于ck0等級的置信度為λ，或說低于ck0等級的置信度是1－λ。

2 綜合評價算例

根據上述未確知測度評價模型，以邯鄲市邯三建筑有限公司的20名中層以上核心職工為例進行測評。參評的專家及領導10人，分別在品德素質、智力素質、績效評價、身體評價和能力素質五個方面，共30個評價指標進行評測。評價指標體系如表1所示。評語空間為{優，良，中，一般，差}。

測評方式:采用專家打分，關鍵是確定合理的打分規則。在這30項指標中，規定每項指標以10分計，分布于5個評語等級上。不同的等級分使待評對象處于不同的測評等級。這種打分規則避開了指標重要性權重;另一種規則是:每項指標滿分10分，每個待評對象在0～10間得到一個分值;再用指標重要性權重乘以得分，并按總分進行分類。但這要求估計指標重要性權重。每個待評對象均得10分，區別在于每個待評對象的等級分不同。這樣的打分原則是公正的，也符合“非負有界性、可加性、歸一性”的測量準則。10名專家對20名職工按上述原則逐一“打分”，統計打分結果，取平均值并作整數化處理得到，待評對象1的得分如表2所示。

表1 指標體系結構Tab.1 Index system structure

表2 對象1的測評統計得分表Tab.2 Assessment statistical scoring sheets of object 1

根據表2的統計數據得到如下單指標測度矩陣:

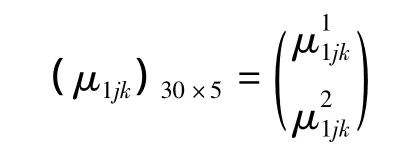
其中

根據式(3)－式(6)計算指標分類權重，關于對象1的各指標分類權重向量為

由上式計算對象1的評價向量為

取 λ =0.6 有:當 k0=2 時，0.37 70+0.310 7+0.687 7 ＞0.6= λ

因此，對象1被評價為良，同理可對其余待評對象進行測評。此測評結果相對合理，領導及專家比較滿意。

3 與模糊綜合評判模型的區別

人才測評方法雖很多，各有優點和不足。最為典型的方法是模糊綜合評判模型。本文方法與模糊綜合評判的主要不同在于:(1)本文方法要求每個測評對象的單指標測度必須滿足關于測量的三條準則。對于人才測評，各單指標測度是由專家“打分”的方法得出，那么打分應體現“公正”原則:每個測評對象在每項指標上均得10分，這10分分布在不同的測評等級上。這就是公平性原則，由此得到的單指標測度顯然滿足關于測量的三條準則。(2)合成測度是各單指標測度的加權平均，而“權”是各指標的分類權重，而指標的分類權重是由對象關于指標的觀測值提供的分類信息計算求得的，它的語意是該指標對對象分類做出貢獻的大小。這一點是本文方法與模糊綜合評判合成可信度中最本質的區別;在模糊測評合成可信度中用的是指標的重要性權重，指標重要性權重是由專家主觀擬定的。事實上，專家主觀擬定的指標重要性權重與觀測值無關，它對所有待評對象具有通用性，因為沒有對特定的待評對象提供針對性的分類信息，因而不能用于特定對象分類。

4 結語

應用本文模型的測評結果由矩陣(1)完全確定，除此之外，不再需要任何先驗信息。本文確定的打分規則:每個待評對象在每項指標上均得10分，區別在于不同評語等級上的得分不同，從測量角度講是合理的。

［1] 梁建.人事測評技術及其理論發展［J] .外國經濟與管理，2000，22(7):19－23.

［2] 張德新，崔 巍，艾慶生.人才素質的模糊評價［J] .電腦與信息技術，2010(5):8－9.

［3] 高勇強.人事考核的多層次模糊綜合評判法［J] .中國管理科學，2010，8(2):44－49.

［4] 梁 鎮，劉 巖.我國人才測評技術發展現狀分析［J] .商業研究，2002，38(1):35－37.

［5] 牛麗文，夏冬艷，任麗媛.基于未確知測度的企業業績評價模型研究［J] .河北建筑科技學院學報，2006，26(3):91－94.

［6] 李萬慶，張立寧，孟文清.基于信息熵與未確知測度的MIS綜合評價模型研究［J] .河北建筑科技學院學報，2005，22(3):49－53.

［7] 王曉波.基于未確知測度理論的CCPM緩沖區尺寸設計［J] .河北工程大學學報:自然科學版 ，2011，28(1):76－80.

［8] 曹慶奎，李琴，于兵.基于未確知測度的高新區技術創新環境評價［J] .科技進步與對策，2009，26(9):124－127.

［9] 曹慶奎，李建光，楊艷麗.基于信息熵和灰關聯分析的煤礦企業供應商評價選擇研究［J] .河北工程大學學報:自然科學版，2008，25(1):81－84.

［10] 吳茂森.概率與信息［M] .上海:科學技術出版社，1960.